2020-2021学年人教版数学八下册18.2.3正方形-课件(共22张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八下册18.2.3正方形-课件(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
18.2.3
正方形
人教版
八年级数学下册
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
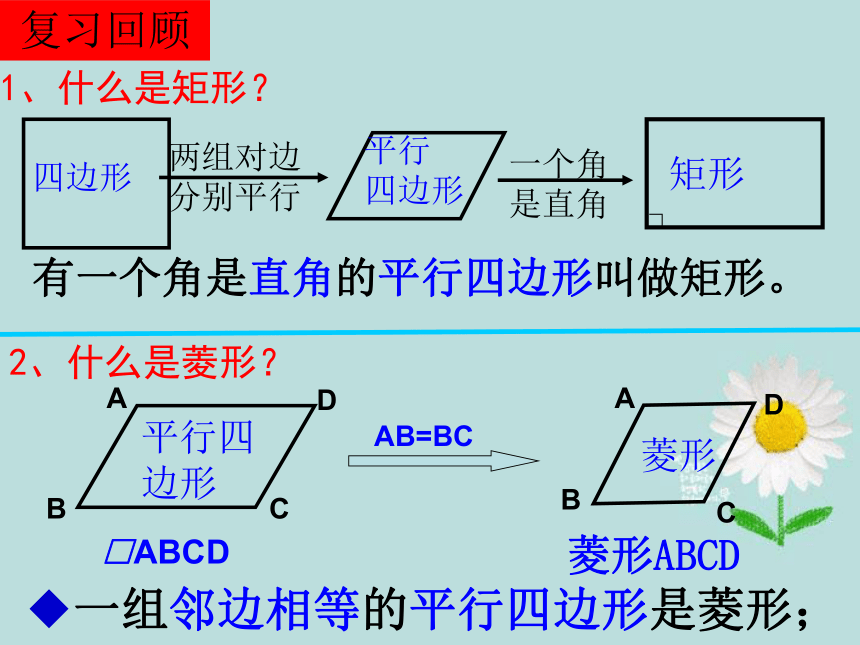
有一个角是直角的平行四边形叫做矩形。
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
一组邻边相等的平行四边形是菱形;
平行四边形
菱形
1、什么是矩形?
2、什么是菱形?
正方形
矩形
矩形纸片怎样折叠出正方形?
探
究(一)
邻边相等的矩形是正方形
探
究(二)
菱形怎样变化后就成了正方形呢?
正方形
有一个角是直角的菱形是正方形
探究小结
矩
形
〃
〃
正方形
邻边
相等
〃
〃
发现:
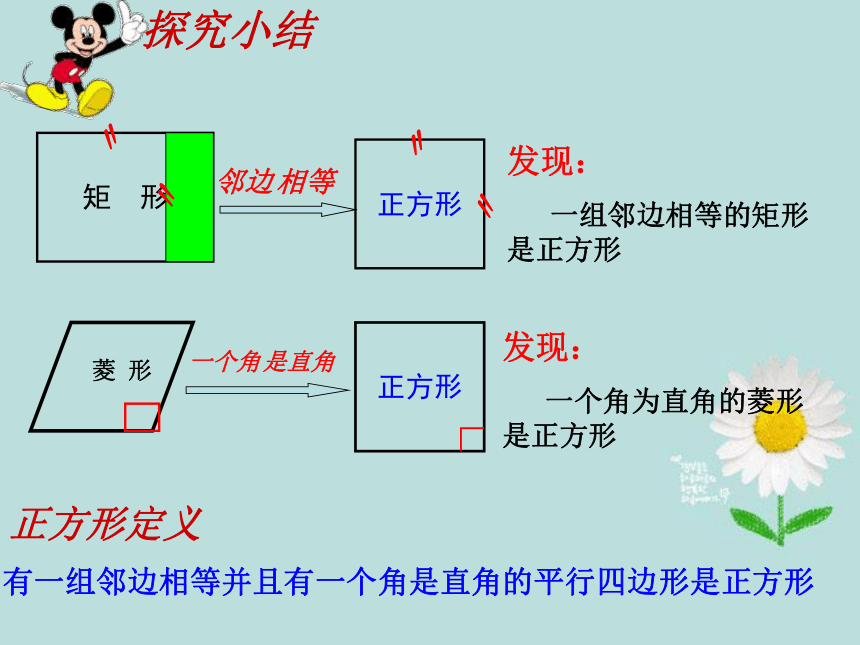
一组邻边相等的矩形
是正方形
菱
形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
拓展讨论
正方形有哪些性质?
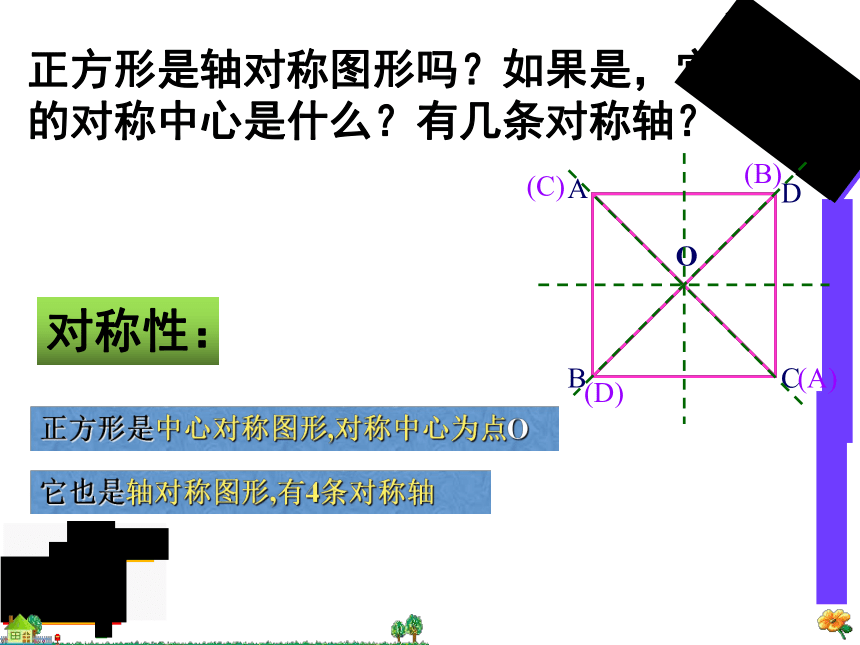
正方形是中心对称图形,对称中心为点O
它也是轴对称图形,有4条对称轴
O
A
B
C
D
(A)
(B)
(C)
(D)
对称性:
正方形是轴对称图形吗?如果是,它的对称中心是什么?有几条对称轴?
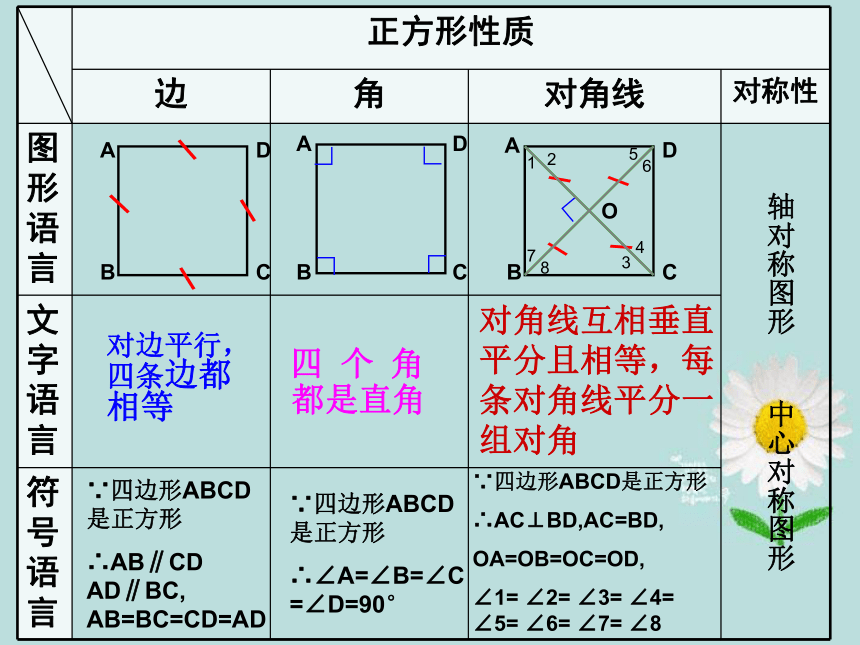
正方形性质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=
∠2=
∠3=
∠4=
∠5=
∠6=
∠7=
∠8
轴对称图形
中心对称图形
1
2
3
4
5
6
7
8
平行四边形
矩形
菱形
正
方
形
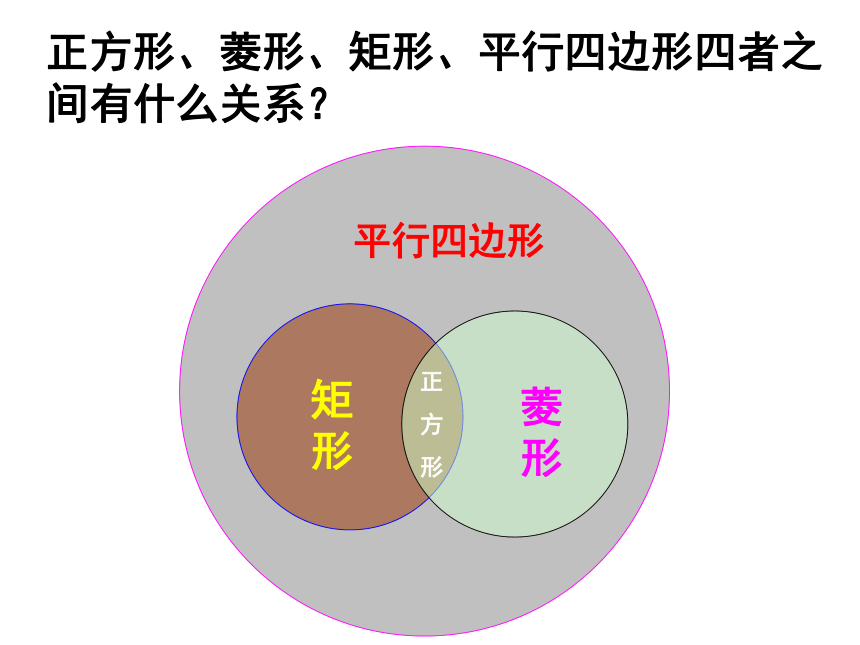
正方形、菱形、矩形、平行四边形四者之间有什么关系?
小结:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
平行四边形
有一组邻边相等
有一个角是直角
正方形常见的判定法
例
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对
角线AC、BD相交于点O.
求证:△ABO、
△BCO、
△CDO、
△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO
小结:
正方形的两条对角线把这个正方形分成
四个全等的等腰直角三角形.
正方形对角线把正方形分成多少个等腰直角三角形?
A
D
C
B
O
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、
△ADC、
△ABD、
△BCD
;
△AOB、
△BOC、
△COD、
△DOA.
已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
例2
证明:∵
四边形ABCD是正方形,
∴
∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等).
又
DG⊥AE,
∴
∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴
∠EAO=∠FDO.
∴
△AEO
≌△DFO.
∴
OE=OF.
随堂练习
P101练习1、2
练习1:证明有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
A
D
C
B
E
∟
∟
练习2:寻找直角三角形,运用直角三角形
求边长和对角线.
1、如图,正方形ABCD的边长为4cm,则图中阴影部分
的面积为
平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC=
cm,
求正方形DEFG的边长.
补充练习
3、在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
补充练习
课堂小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质?
对边平行,四条边都相等
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
对角线:
3、正方形常见的几种判定方法?
四个角都是直角
角:
(3)有一组邻边相等且有一个角是直角的平行四边形是正方形
(2)有一组邻边相等的矩形是正方形
(1)有一个角是直角的菱形是正方形
生活中正方形
生活中正方形
1、习题18.2第8
、15题
作业布置
谢谢指导!
谢谢指导!
18.2.3
正方形
人教版
八年级数学下册
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
有一个角是直角的平行四边形叫做矩形。
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
一组邻边相等的平行四边形是菱形;
平行四边形
菱形
1、什么是矩形?
2、什么是菱形?
正方形
矩形
矩形纸片怎样折叠出正方形?
探
究(一)
邻边相等的矩形是正方形
探
究(二)
菱形怎样变化后就成了正方形呢?
正方形
有一个角是直角的菱形是正方形
探究小结
矩
形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形
是正方形
菱
形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
拓展讨论
正方形有哪些性质?
正方形是中心对称图形,对称中心为点O
它也是轴对称图形,有4条对称轴
O
A
B
C
D
(A)
(B)
(C)
(D)
对称性:
正方形是轴对称图形吗?如果是,它的对称中心是什么?有几条对称轴?
正方形性质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1=
∠2=
∠3=
∠4=
∠5=
∠6=
∠7=
∠8
轴对称图形
中心对称图形
1
2
3
4
5
6
7
8
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
小结:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
平行四边形
有一组邻边相等
有一个角是直角
正方形常见的判定法
例
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对
角线AC、BD相交于点O.
求证:△ABO、
△BCO、
△CDO、
△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO
小结:
正方形的两条对角线把这个正方形分成
四个全等的等腰直角三角形.
正方形对角线把正方形分成多少个等腰直角三角形?
A
D
C
B
O
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、
△ADC、
△ABD、
△BCD
;
△AOB、
△BOC、
△COD、
△DOA.
已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
例2
证明:∵
四边形ABCD是正方形,
∴
∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等).
又
DG⊥AE,
∴
∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴
∠EAO=∠FDO.
∴
△AEO
≌△DFO.
∴
OE=OF.
随堂练习
P101练习1、2
练习1:证明有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
A
D
C
B
E
∟
∟
练习2:寻找直角三角形,运用直角三角形
求边长和对角线.
1、如图,正方形ABCD的边长为4cm,则图中阴影部分
的面积为
平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC=
cm,
求正方形DEFG的边长.
补充练习
3、在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
补充练习
课堂小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质?
对边平行,四条边都相等
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
对角线:
3、正方形常见的几种判定方法?
四个角都是直角
角:
(3)有一组邻边相等且有一个角是直角的平行四边形是正方形
(2)有一组邻边相等的矩形是正方形
(1)有一个角是直角的菱形是正方形
生活中正方形
生活中正方形
1、习题18.2第8
、15题
作业布置
谢谢指导!
谢谢指导!
