2-3 2.4 正态分布 学生版Word无答案
文档属性
| 名称 | 2-3 2.4 正态分布 学生版Word无答案 | 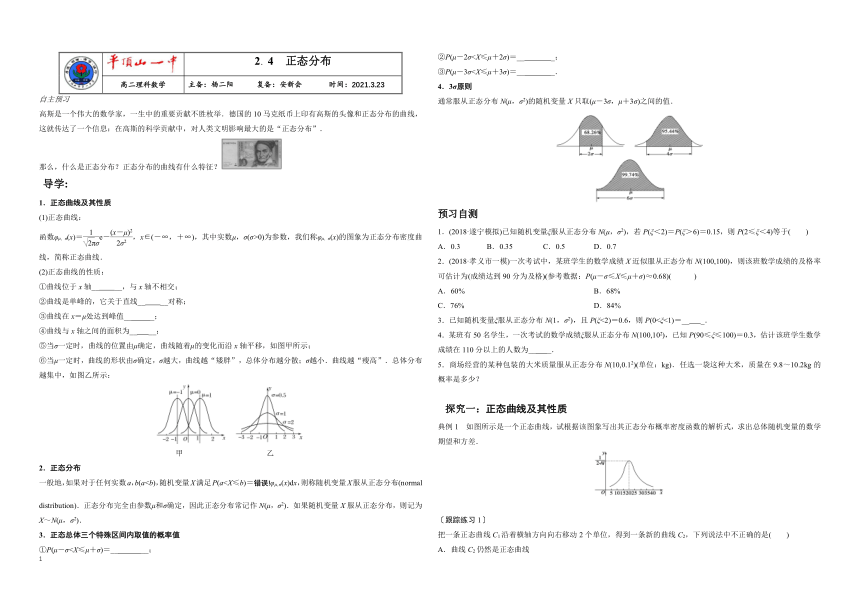 | |
| 格式 | zip | ||
| 文件大小 | 385.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 11:57:44 | ||
图片预览


文档简介
2.4 正态分布
高二理科数学
主备:杨二阳
复备:安新会
时间:2021.3.23
自主预习
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文明影响最大的是“正态分布”.
那么,什么是正态分布?正态分布的曲线有什么特征?
导学:
1.正态曲线及其性质
(1)正态曲线:
函数φμ,σ(x)=e-,x∈(-∞,+∞),其中实数μ,σ(σ>0)为参数,我们称φμ,σ(x)的图象为正态分布密度曲线,简称正态曲线.
(2)正态曲线的性质:
①曲线位于x轴__
__,与x轴不相交;
②曲线是单峰的,它关于直线__
__对称;
③曲线在x=μ处达到峰值__
_;
④曲线与x轴之间的面积为__
__;
⑤当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图甲所示;
⑥当μ一定时,曲线的形状由σ确定,σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中,如图乙所示:
甲 乙
2.正态分布
一般地,如果对于任何实数a,b(adistribution).正态分布完全由参数μ和σ确定,因此正态分布常记作N(μ,σ2).如果随机变量X服从正态分布,则记为X~N(μ,σ2).
3.正态总体三个特殊区间内取值的概率值
①P(μ-σ__;
②P(μ-2σ_;
③P(μ-3σ_.
4.3σ原则
通常服从正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值.
预习自测
1.(2018·遂宁模拟)已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.15,则P(2≤ξ<4)等于( )
A.0.3
B.0.35
C.0.5
D.0.7
2.(2018·孝义市一模)一次考试中,某班学生的数学成绩X近似服从正态分布N(100,100),则该班数学成绩的及格率可估计为(成绩达到90分为及格)(参考数据:P(μ-σ≤X≤μ+σ)≈0.68)(
)
A.60%
B.68%
C.76%
D.84%
3.已知随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.6,则P(0<ξ<1)=__
_.
4.某班有50名学生,一次考试的数学成绩ξ服从正态分布N(100,102),已知P(90≤ξ≤100)=0.3,估计该班学生数学成绩在110分以上的人数为__
_.
5.商场经营的某种包装的大米质量服从正态分布N(10,0.12)(单位:kg).任选一袋这种大米,质量在9.8~10.2kg的概率是多少?
探究一:正态曲线及其性质
典例1 如图所示是一个正态曲线,试根据该图象写出其正态分布概率密度函数的解析式,求出总体随机变量的数学期望和方差.
〔跟踪练习1〕
把一条正态曲线C1沿着横轴方向向右移动2个单位,得到一条新的曲线C2,下列说法中不正确的是( )
A.曲线C2仍然是正态曲线
B.曲线C1和曲线C2的最高点的纵坐标相等
C.以曲线C2为概率密度曲线的总体的期望比以曲线C1为概率密度曲线的总体的期望大2
D.以曲线C2为概率密度曲线的总体的方差比以曲线C1为概率密度曲线的总体的方差大2
探究二:利用正态分布的对称性求概率
典例2 (1)已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2<ξ<2)=(
)
A.0.477
B.0.625
C.0.954
D.0.977
(2)(2017·临沂高二检测)设随机变量ξ服从正态分布N(2,σ2),若P(ξ>c)=a,则P(ξ>4-c)等于(
)
A.a
B.1-a
C.2a
D.1-2a
〔跟踪练习2〕
为了了解某地区高三男生的身体发育状况,抽查了该地区1000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5kg小于等于62.5kg属于正常情况,则这1000名男生中属于正常情况的人数是(
)
A.997 B.954
C.819
D.683
探究三:正态分布的应用
典例3 某厂生产的圆柱形零件的外径尺寸X~N(4,0.25).质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外径为5.7cm,试问该厂生产的这批零件是否合格?
〔跟踪练习3〕
在某次数学考试中,考生的成绩服从一个正态分布,即ξ~N(90,100).
(1)试求考试成绩ξ位于区间(70,110]内的概率;
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]间的考生大约有多少人.
典例4 某厂生产的产品,质量要求服从正态分布
N(100,4),现从产品中抽取了10件,测得质量分别为102,92,104,103,98,96,97,99,101,108,则该生产线是否要停产检修?
〔跟踪练习4〕
假设某省今年高考考生成绩服从正态分布N(500,1002),某校有考生2400人,试估计成绩在下列范围内的考生人数.
(1)(400,600];
(2)(300,700].
要准确应用正态分布的对称性转化
典例5 随机变量ξ服从正态分布N(0,1),如果P(ξ≤1)=0.8413,求P(-1<ξ≤0).
课后练习:
已知随机变量ξ服从正态分布N(1,4),则P(1<ξ≤3)=( B )
(参考数据:若随机变量ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544,P(μ-3σ<ξ<μ+3σ)=0.9974)
A.0.6826 B.0.3413
C.0.9544 D.0.4772
课堂达标验收
1.下列函数可以作为正态分布密度函数的是(
)
A.f(x)=e-
B.f(x)=e
C.f(x)=e-
D.f(x)=e-
2.若X~N(-2,),则X落在(-3.5,-0.5]内的概率是(
)
A.95.45%
B.99.73%
C.4.55%
D.0.27%
3.(2018·全国一模)在某次学科知识竞赛中(总分100分),若参赛学生成绩ξ服从N(80,σ2)(σ>0),若ξ在(70,90)内的概率为0.8,则落在[90,100]内的概率为( )
A.0.05
B.0.1
C.0.15
D.0.2
4.(2018·江门一模)已知随机变量ξ~N(1,4),且P(ξ<3)=0.84,则P(-1<ξ<1)=__
__.
5.(2018·唐山模拟)已知随机变量ξ~N(1,σ2),若P(ξ>3)=0.2,则P(ξ≥-1)=__
__.
课时作业
A级 基础巩固
一、选择题
1.已知一次考试共有60名同学参加,考生的成绩X~N(110,52),据此估计,大约应有57人的分数在下列哪个区间内( )
A.(90,110]
B.(95,125]
C.(100,120]
D.(105,115]
2.(2018·呼和浩特二模)有10000人参加某次考试,其成绩X近似服从正态分布N(100,132).P(61<X<139)=0.997.则此次考试中成绩不低于139分的人数约为( )
A.10
B.30
C.15
D.23
3.如图是当σ取三个不同值σ1,σ2,σ3时的三种正态曲线,那么σ1,σ2,σ3的大小关系是( D )
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>σ3>0
D.0<σ1<σ2=1<σ3
4.某厂生产的零件外直径X~N(8.0,0.0225),单位mm,今从该厂上、下午生产的零件中各随机取出一个,测得其外直径分别为7.9mm和7.5mm,则可认为( C )
A.上、下午生产情况均为正常
B.上、下午生产情况均为异常
C.上午生产情况正常,下午生产情况异常
D.上午生产情况异常,下午生产情况正常
5.某市进行一次高三教学质量抽样检测,考试后统计的所有考生的数学成绩服从正态分布.已知数学成绩平均分为90分,60分以下的人数占10%,则数学成绩在90分至120分之间的考生人数所占百分比约为( )
A.10%
B.20%
C.30%
D.40%
6.以Φ(x)表示标准正态总体在区间(-∞,x)内取值的概率,若随机变量ξ服从正态分布N(μ,σ2),则概率P(|ξ-μ|<σ)等于( )
A.Φ(μ+σ)-Φ(μ-σ)
B.Φ(1)-Φ(-1)
C.Φ
D.2Φ(μ+σ)
二、填空题
7.正态变量的概率密度函数f(x)=e-,x∈R的图象关于直线__
_对称,f(x)的最大值为____.
8.(2018·凉山州模拟)已知离散型随机变量ξ服从正态分布N~(2,1),且P(ξ<3)=0.968,则P(1<ξ<3)=__
__.
9.已知正态分布N(μ,σ2)的密度曲线是f(x)=e-,x∈R.给出以下四个命题:
①对任意x∈R,f(μ+x)=f(μ-x)成立;
②如果随机变量X服从N(μ,σ2),且F(x)=P(X③如果随机变量X服从N(108,100),那么X的期望是108,标准差是100;
④随机变量X服从N(μ,σ2),P(X<1)=,P(X>2)=p,则P(0其中真命题的序号是__
__.(写出所有真命题的序号)
三、解答题
10.某个工厂的工人月收入服从正态分布N(500,202),该工厂共有1200名工人,试估计月收入在440元以下和560元以上的工人大约有多少?
B级 素养提升
一、选择题
1.设X~N(μ1,σ),Y~N(μ2,σ),这两个正态分布密度曲线如图所示.下列结论中正确的是( C )
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)≥P(Y≤t)
D.对任意正数t,P(X≥t)≥P(Y≥t)
2.(2018·德阳模拟)为弘扬我国优秀的传统文化,市教育局对全市所有中小学生进行了“成语”听写测试,经过大数据分析,发现本次听写测试成绩服从正态分布N(78,16).试根据正态分布的相关知识估计测试成绩不小于90的学生所占的百分比为( )参考数据:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974.(
)
A.0.13%
B.1.3%
C.3%
D.3.3%
二、填空题
3.(2018·黔东南州一模)黔东南州雷山西江千户苗寨,是目前中国乃至全世界最大的苗族聚居村寨,每年来自世界各地的游客络绎不绝.假设每天到西江苗寨的游客人数ξ是服从正态分布N(2000,10000)的随机变量.则每天到西江苗寨的游客人数超过2100的概率为__
__.(参考数据:若ξ服从N(μ,δ2),有P(μ-δ<ξ≤μ+δ)=0.6826,P(μ-2δ<ξ≤μ+2δ)=0.9544,P(μ-3δ<ξ≤μ+3δ)=0.9974)
4.设某城市居民私家车平均每辆车每月汽油费用为随机变量ξ(单位为:元),经统计得ξ~N(520,14
400),从该城市私家车中随机选取容量为10
000的样本,其中每月汽油费用在(400,640)之间的私家车估计有__
__辆.
(附:若ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544,P(μ-3σ<ξ<μ+3σ)=0.9974)
三、解答题
5.一投资者在两个投资方案中选择一个,这两个投资方案的利润X(万元)分别服从正态分布N(8,32)和N(7,12),投资者要求“利润超过5万元”的概率尽量大,那么他应该选择哪一个方案?
6.某市教育局为了了解高三学生体育达标情况,对全市高三学生进行了体能测试,经分析,全市学生体能测试成绩X服从正态分布N(80,σ2)(满分为100分),已知P(X<75)=0.3,P(X≥95)=0.1,现从该市高三学生中随机抽取三位同学.
(1)求抽到的三位同学该次体能测试成绩在区间[80,85),[85,95),[95,100]内各有一位同学的概率;
(2)记抽到的三位同学该次体能测试成绩在区间[75,85]的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
3
高二理科数学
主备:杨二阳
复备:安新会
时间:2021.3.23
自主预习
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文明影响最大的是“正态分布”.
那么,什么是正态分布?正态分布的曲线有什么特征?
导学:
1.正态曲线及其性质
(1)正态曲线:
函数φμ,σ(x)=e-,x∈(-∞,+∞),其中实数μ,σ(σ>0)为参数,我们称φμ,σ(x)的图象为正态分布密度曲线,简称正态曲线.
(2)正态曲线的性质:
①曲线位于x轴__
__,与x轴不相交;
②曲线是单峰的,它关于直线__
__对称;
③曲线在x=μ处达到峰值__
_;
④曲线与x轴之间的面积为__
__;
⑤当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图甲所示;
⑥当μ一定时,曲线的形状由σ确定,σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中,如图乙所示:
甲 乙
2.正态分布
一般地,如果对于任何实数a,b(a
3.正态总体三个特殊区间内取值的概率值
①P(μ-σ
②P(μ-2σ
③P(μ-3σ
4.3σ原则
通常服从正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值.
预习自测
1.(2018·遂宁模拟)已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.15,则P(2≤ξ<4)等于( )
A.0.3
B.0.35
C.0.5
D.0.7
2.(2018·孝义市一模)一次考试中,某班学生的数学成绩X近似服从正态分布N(100,100),则该班数学成绩的及格率可估计为(成绩达到90分为及格)(参考数据:P(μ-σ≤X≤μ+σ)≈0.68)(
)
A.60%
B.68%
C.76%
D.84%
3.已知随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.6,则P(0<ξ<1)=__
_.
4.某班有50名学生,一次考试的数学成绩ξ服从正态分布N(100,102),已知P(90≤ξ≤100)=0.3,估计该班学生数学成绩在110分以上的人数为__
_.
5.商场经营的某种包装的大米质量服从正态分布N(10,0.12)(单位:kg).任选一袋这种大米,质量在9.8~10.2kg的概率是多少?
探究一:正态曲线及其性质
典例1 如图所示是一个正态曲线,试根据该图象写出其正态分布概率密度函数的解析式,求出总体随机变量的数学期望和方差.
〔跟踪练习1〕
把一条正态曲线C1沿着横轴方向向右移动2个单位,得到一条新的曲线C2,下列说法中不正确的是( )
A.曲线C2仍然是正态曲线
B.曲线C1和曲线C2的最高点的纵坐标相等
C.以曲线C2为概率密度曲线的总体的期望比以曲线C1为概率密度曲线的总体的期望大2
D.以曲线C2为概率密度曲线的总体的方差比以曲线C1为概率密度曲线的总体的方差大2
探究二:利用正态分布的对称性求概率
典例2 (1)已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2<ξ<2)=(
)
A.0.477
B.0.625
C.0.954
D.0.977
(2)(2017·临沂高二检测)设随机变量ξ服从正态分布N(2,σ2),若P(ξ>c)=a,则P(ξ>4-c)等于(
)
A.a
B.1-a
C.2a
D.1-2a
〔跟踪练习2〕
为了了解某地区高三男生的身体发育状况,抽查了该地区1000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5kg小于等于62.5kg属于正常情况,则这1000名男生中属于正常情况的人数是(
)
A.997 B.954
C.819
D.683
探究三:正态分布的应用
典例3 某厂生产的圆柱形零件的外径尺寸X~N(4,0.25).质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外径为5.7cm,试问该厂生产的这批零件是否合格?
〔跟踪练习3〕
在某次数学考试中,考生的成绩服从一个正态分布,即ξ~N(90,100).
(1)试求考试成绩ξ位于区间(70,110]内的概率;
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]间的考生大约有多少人.
典例4 某厂生产的产品,质量要求服从正态分布
N(100,4),现从产品中抽取了10件,测得质量分别为102,92,104,103,98,96,97,99,101,108,则该生产线是否要停产检修?
〔跟踪练习4〕
假设某省今年高考考生成绩服从正态分布N(500,1002),某校有考生2400人,试估计成绩在下列范围内的考生人数.
(1)(400,600];
(2)(300,700].
要准确应用正态分布的对称性转化
典例5 随机变量ξ服从正态分布N(0,1),如果P(ξ≤1)=0.8413,求P(-1<ξ≤0).
课后练习:
已知随机变量ξ服从正态分布N(1,4),则P(1<ξ≤3)=( B )
(参考数据:若随机变量ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544,P(μ-3σ<ξ<μ+3σ)=0.9974)
A.0.6826 B.0.3413
C.0.9544 D.0.4772
课堂达标验收
1.下列函数可以作为正态分布密度函数的是(
)
A.f(x)=e-
B.f(x)=e
C.f(x)=e-
D.f(x)=e-
2.若X~N(-2,),则X落在(-3.5,-0.5]内的概率是(
)
A.95.45%
B.99.73%
C.4.55%
D.0.27%
3.(2018·全国一模)在某次学科知识竞赛中(总分100分),若参赛学生成绩ξ服从N(80,σ2)(σ>0),若ξ在(70,90)内的概率为0.8,则落在[90,100]内的概率为( )
A.0.05
B.0.1
C.0.15
D.0.2
4.(2018·江门一模)已知随机变量ξ~N(1,4),且P(ξ<3)=0.84,则P(-1<ξ<1)=__
__.
5.(2018·唐山模拟)已知随机变量ξ~N(1,σ2),若P(ξ>3)=0.2,则P(ξ≥-1)=__
__.
课时作业
A级 基础巩固
一、选择题
1.已知一次考试共有60名同学参加,考生的成绩X~N(110,52),据此估计,大约应有57人的分数在下列哪个区间内( )
A.(90,110]
B.(95,125]
C.(100,120]
D.(105,115]
2.(2018·呼和浩特二模)有10000人参加某次考试,其成绩X近似服从正态分布N(100,132).P(61<X<139)=0.997.则此次考试中成绩不低于139分的人数约为( )
A.10
B.30
C.15
D.23
3.如图是当σ取三个不同值σ1,σ2,σ3时的三种正态曲线,那么σ1,σ2,σ3的大小关系是( D )
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>σ3>0
D.0<σ1<σ2=1<σ3
4.某厂生产的零件外直径X~N(8.0,0.0225),单位mm,今从该厂上、下午生产的零件中各随机取出一个,测得其外直径分别为7.9mm和7.5mm,则可认为( C )
A.上、下午生产情况均为正常
B.上、下午生产情况均为异常
C.上午生产情况正常,下午生产情况异常
D.上午生产情况异常,下午生产情况正常
5.某市进行一次高三教学质量抽样检测,考试后统计的所有考生的数学成绩服从正态分布.已知数学成绩平均分为90分,60分以下的人数占10%,则数学成绩在90分至120分之间的考生人数所占百分比约为( )
A.10%
B.20%
C.30%
D.40%
6.以Φ(x)表示标准正态总体在区间(-∞,x)内取值的概率,若随机变量ξ服从正态分布N(μ,σ2),则概率P(|ξ-μ|<σ)等于( )
A.Φ(μ+σ)-Φ(μ-σ)
B.Φ(1)-Φ(-1)
C.Φ
D.2Φ(μ+σ)
二、填空题
7.正态变量的概率密度函数f(x)=e-,x∈R的图象关于直线__
_对称,f(x)的最大值为____.
8.(2018·凉山州模拟)已知离散型随机变量ξ服从正态分布N~(2,1),且P(ξ<3)=0.968,则P(1<ξ<3)=__
__.
9.已知正态分布N(μ,σ2)的密度曲线是f(x)=e-,x∈R.给出以下四个命题:
①对任意x∈R,f(μ+x)=f(μ-x)成立;
②如果随机变量X服从N(μ,σ2),且F(x)=P(X
④随机变量X服从N(μ,σ2),P(X<1)=,P(X>2)=p,则P(0
__.(写出所有真命题的序号)
三、解答题
10.某个工厂的工人月收入服从正态分布N(500,202),该工厂共有1200名工人,试估计月收入在440元以下和560元以上的工人大约有多少?
B级 素养提升
一、选择题
1.设X~N(μ1,σ),Y~N(μ2,σ),这两个正态分布密度曲线如图所示.下列结论中正确的是( C )
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)≥P(Y≤t)
D.对任意正数t,P(X≥t)≥P(Y≥t)
2.(2018·德阳模拟)为弘扬我国优秀的传统文化,市教育局对全市所有中小学生进行了“成语”听写测试,经过大数据分析,发现本次听写测试成绩服从正态分布N(78,16).试根据正态分布的相关知识估计测试成绩不小于90的学生所占的百分比为( )参考数据:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974.(
)
A.0.13%
B.1.3%
C.3%
D.3.3%
二、填空题
3.(2018·黔东南州一模)黔东南州雷山西江千户苗寨,是目前中国乃至全世界最大的苗族聚居村寨,每年来自世界各地的游客络绎不绝.假设每天到西江苗寨的游客人数ξ是服从正态分布N(2000,10000)的随机变量.则每天到西江苗寨的游客人数超过2100的概率为__
__.(参考数据:若ξ服从N(μ,δ2),有P(μ-δ<ξ≤μ+δ)=0.6826,P(μ-2δ<ξ≤μ+2δ)=0.9544,P(μ-3δ<ξ≤μ+3δ)=0.9974)
4.设某城市居民私家车平均每辆车每月汽油费用为随机变量ξ(单位为:元),经统计得ξ~N(520,14
400),从该城市私家车中随机选取容量为10
000的样本,其中每月汽油费用在(400,640)之间的私家车估计有__
__辆.
(附:若ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544,P(μ-3σ<ξ<μ+3σ)=0.9974)
三、解答题
5.一投资者在两个投资方案中选择一个,这两个投资方案的利润X(万元)分别服从正态分布N(8,32)和N(7,12),投资者要求“利润超过5万元”的概率尽量大,那么他应该选择哪一个方案?
6.某市教育局为了了解高三学生体育达标情况,对全市高三学生进行了体能测试,经分析,全市学生体能测试成绩X服从正态分布N(80,σ2)(满分为100分),已知P(X<75)=0.3,P(X≥95)=0.1,现从该市高三学生中随机抽取三位同学.
(1)求抽到的三位同学该次体能测试成绩在区间[80,85),[85,95),[95,100]内各有一位同学的概率;
(2)记抽到的三位同学该次体能测试成绩在区间[75,85]的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
3
