第十八章 平行四边形 单元同步测试卷(含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元同步测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.如图,正方形ABCD中,E是BD上一点,BE=BC,则∠BEC的度数是(
)
A.45°
B.60°
C.67.5°
D.82.5°
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6
cm,则AB的长是(
)
A.3
cm
B.6
cm
C.10
cm
D.12
cm
3.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50
cm,当它的一端B着地时,另一端A离地面的高度AC为( )
A.25
cm
B.50
cm
C.75
cm
D.100
cm
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
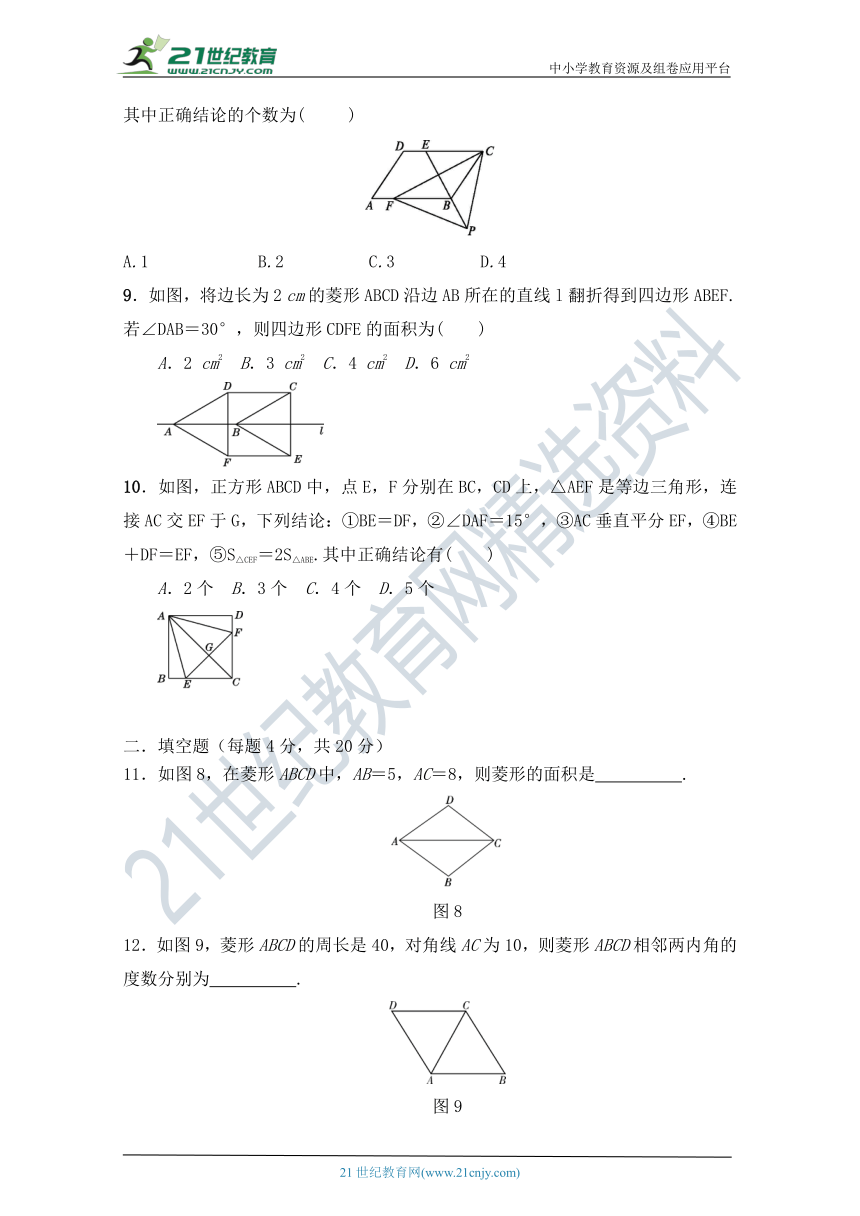
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;
②CF平分∠DCB;
③BC=FB;
④PF=PC.
其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
9.如图,将边长为2
cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF.若∠DAB=30°,则四边形CDFE的面积为( )
A.2
cm2
B.3
cm2
C.4
cm2
D.6
cm2
10.如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )
A.2个
B.3个
C.4个
D.5个
二.填空题(每题4分,共20分)
11.如图8,在菱形ABCD中,AB=5,AC=8,则菱形的面积是
.
图8
12.如图9,菱形ABCD的周长是40,对角线AC为10,则菱形ABCD相邻两内角的度数分别为
.
图9
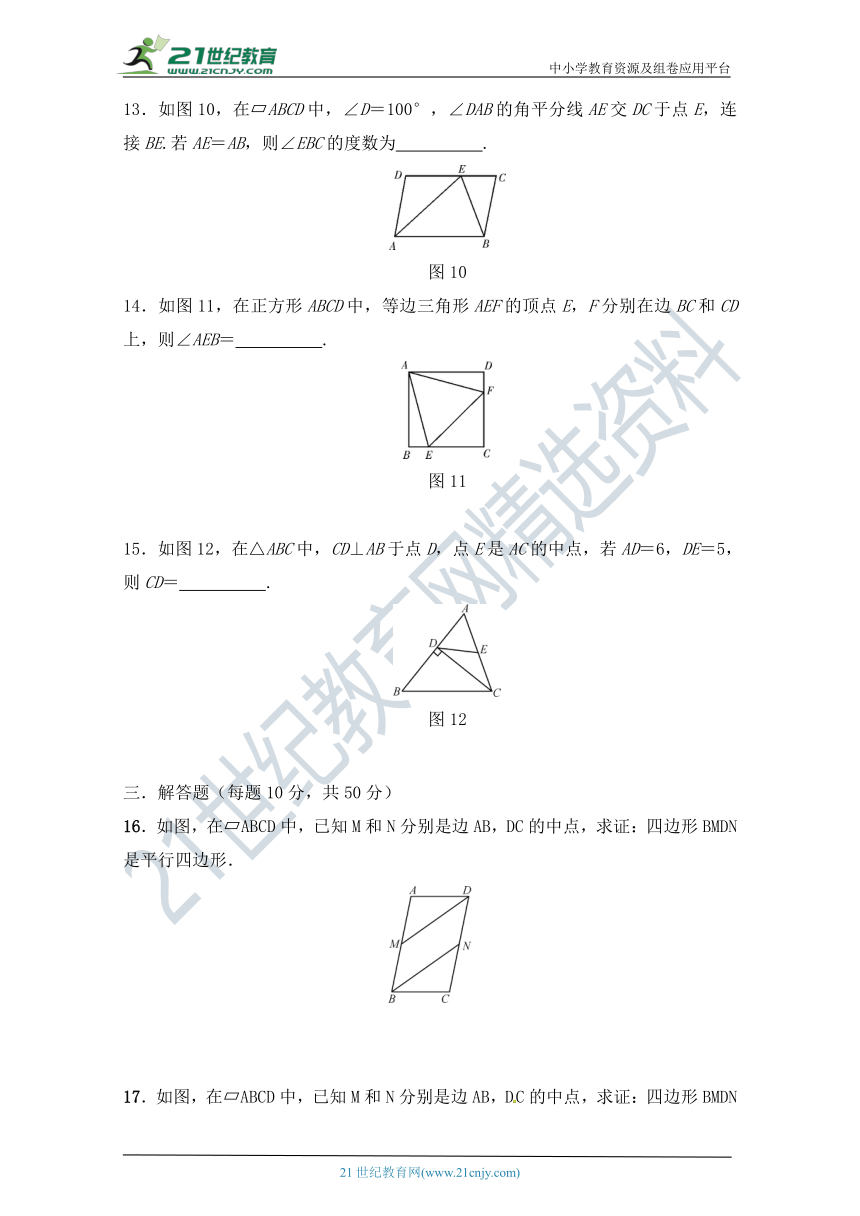
13.如图10,在?ABCD中,∠D=100°,∠DAB的角平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
图10
14.如图11,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=
.
图11
15.如图12,在△ABC中,CD⊥AB于点D,点E是AC的中点,若AD=6,DE=5,则CD=
.
图12
三.解答题(每题10分,共50分)
16.如图,在?ABCD中,已知M和N分别是边AB,DC的中点,求证:四边形BMDN是平行四边形.
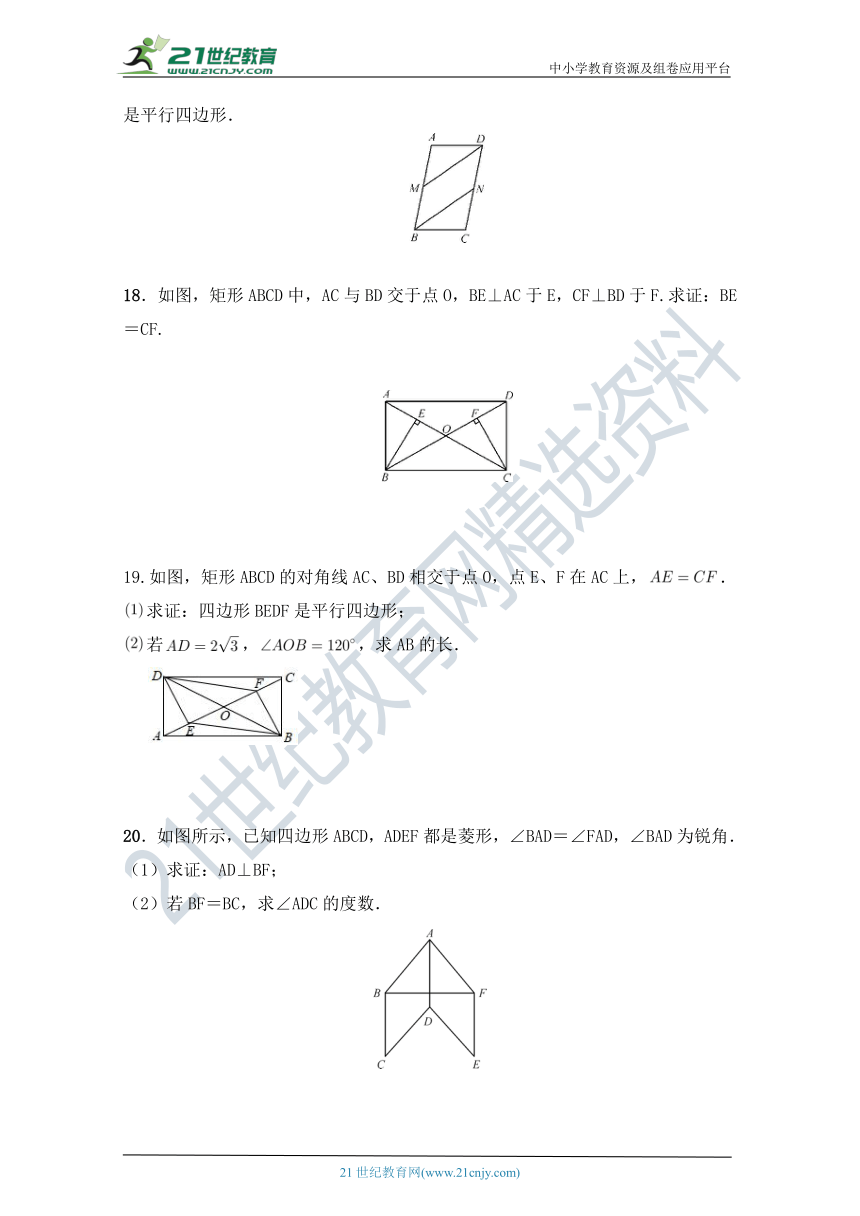
17.如图,在?ABCD中,已知M和N分别是边AB,DC的中点,求证:四边形BMDN是平行四边形.
18.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
19.如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,.
求证:四边形BEDF是平行四边形;
若,,求AB的长.
20.如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
21.问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连接AF,BE.
特例探究:如图1,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;
拓展应用:如图2,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为____________.
参考答案
一.选择题
1.
C
2.
A.
3.
D.
4.
D.
5.
A.
6.
A.
7.
C.
8.
D.
9.
C.
10.C
二.填空题(共5小题)
11.24 12.60°,120° 13.30°
14.75°
15.8
三.解答题(共5小题)
16.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC.∵M和N分别是AB,DC的中点,∴BM=AB,DN=DC.∴BM=DN.∴四边形BMDN是平行四边形.
17.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC.∵M和N分别是AB,DC的中点,∴BM=AB,DN=DC.∴BM=DN.∴四边形BMDN是平行四边形.
18.证明:∵四边形ABCD为矩形,∴OB=OC.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF(AAS).∴BE=CF.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20.(1)证明:连接DB,DF.∵四边形ABCD,ADEF都是菱形,∴AB=BC=CD=DA=DE=EF=FA.在△BAD和△FAD中,∴△BAD≌△FAD(SAS).∴DB=DF.∴点D在线段BF的垂直平分线上.∵AB=AF,∴A在线段BF的垂直平分线上.∴AD是线段BF的垂直平分线.∴AD⊥BF.(2)设AD⊥BF于H,作DG⊥BC于G,则四边形BGDH是矩形.∴DG=BH=BF.∵BF=BC,BC=CD,∴DG=CD.在Rt△CDG中,∵∠CGD=90°,DG=CD,∴∠C=30°.又∵BC∥AD,∴∠ADC=180°-∠C=150°.
21.特例探究:AF=BE,AF⊥BE.理由:四边形ABCD为正方形,△ADE与△DCF均为等边三角形,∴AB=AD=CD,∠BAD=∠ADC,AE=AD=CD=DF,∠DAE=∠CDF.∴∠BAD+∠DAE=∠ADC+∠CDF,即∠BAE=∠ADF.在△ABE和△DAF中,∴△ABE≌△DAF(SAS).∴AF=BE,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴AF⊥BE.
拓展应用:在△ADE和△DCF中,∴△ADE≌△DCF(SSS).∴∠DAE=∠CDF.∴∠ADC+∠CDF=∠BAD+∠EAD,即∠ADF=∠BAE.在△ABE和△DAF中,∴△ABE≌△DAF(SAS).∴AF=BE,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴AF⊥BE.∴S四边形ABFE=AF·BE=×4×4=8.故答案为8.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第18章
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.如图,正方形ABCD中,E是BD上一点,BE=BC,则∠BEC的度数是(
)
A.45°
B.60°
C.67.5°
D.82.5°
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6
cm,则AB的长是(
)
A.3
cm
B.6
cm
C.10
cm
D.12
cm
3.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50
cm,当它的一端B着地时,另一端A离地面的高度AC为( )
A.25
cm
B.50
cm
C.75
cm
D.100
cm
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;
②CF平分∠DCB;
③BC=FB;
④PF=PC.
其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
9.如图,将边长为2
cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF.若∠DAB=30°,则四边形CDFE的面积为( )
A.2
cm2
B.3
cm2
C.4
cm2
D.6
cm2
10.如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )
A.2个
B.3个
C.4个
D.5个
二.填空题(每题4分,共20分)
11.如图8,在菱形ABCD中,AB=5,AC=8,则菱形的面积是
.
图8
12.如图9,菱形ABCD的周长是40,对角线AC为10,则菱形ABCD相邻两内角的度数分别为
.
图9
13.如图10,在?ABCD中,∠D=100°,∠DAB的角平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
图10
14.如图11,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=
.
图11
15.如图12,在△ABC中,CD⊥AB于点D,点E是AC的中点,若AD=6,DE=5,则CD=
.
图12
三.解答题(每题10分,共50分)
16.如图,在?ABCD中,已知M和N分别是边AB,DC的中点,求证:四边形BMDN是平行四边形.
17.如图,在?ABCD中,已知M和N分别是边AB,DC的中点,求证:四边形BMDN是平行四边形.
18.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
19.如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,.
求证:四边形BEDF是平行四边形;
若,,求AB的长.
20.如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
21.问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连接AF,BE.
特例探究:如图1,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;
拓展应用:如图2,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为____________.
参考答案
一.选择题
1.
C
2.
A.
3.
D.
4.
D.
5.
A.
6.
A.
7.
C.
8.
D.
9.
C.
10.C
二.填空题(共5小题)
11.24 12.60°,120° 13.30°
14.75°
15.8
三.解答题(共5小题)
16.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC.∵M和N分别是AB,DC的中点,∴BM=AB,DN=DC.∴BM=DN.∴四边形BMDN是平行四边形.
17.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC.∵M和N分别是AB,DC的中点,∴BM=AB,DN=DC.∴BM=DN.∴四边形BMDN是平行四边形.
18.证明:∵四边形ABCD为矩形,∴OB=OC.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF(AAS).∴BE=CF.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20.(1)证明:连接DB,DF.∵四边形ABCD,ADEF都是菱形,∴AB=BC=CD=DA=DE=EF=FA.在△BAD和△FAD中,∴△BAD≌△FAD(SAS).∴DB=DF.∴点D在线段BF的垂直平分线上.∵AB=AF,∴A在线段BF的垂直平分线上.∴AD是线段BF的垂直平分线.∴AD⊥BF.(2)设AD⊥BF于H,作DG⊥BC于G,则四边形BGDH是矩形.∴DG=BH=BF.∵BF=BC,BC=CD,∴DG=CD.在Rt△CDG中,∵∠CGD=90°,DG=CD,∴∠C=30°.又∵BC∥AD,∴∠ADC=180°-∠C=150°.
21.特例探究:AF=BE,AF⊥BE.理由:四边形ABCD为正方形,△ADE与△DCF均为等边三角形,∴AB=AD=CD,∠BAD=∠ADC,AE=AD=CD=DF,∠DAE=∠CDF.∴∠BAD+∠DAE=∠ADC+∠CDF,即∠BAE=∠ADF.在△ABE和△DAF中,∴△ABE≌△DAF(SAS).∴AF=BE,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴AF⊥BE.
拓展应用:在△ADE和△DCF中,∴△ADE≌△DCF(SSS).∴∠DAE=∠CDF.∴∠ADC+∠CDF=∠BAD+∠EAD,即∠ADF=∠BAE.在△ABE和△DAF中,∴△ABE≌△DAF(SAS).∴AF=BE,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴AF⊥BE.∴S四边形ABFE=AF·BE=×4×4=8.故答案为8.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
