2020-2021学年八年级数学北师大版下册 第一章_三角形的证明 单元综合测试(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第一章_三角形的证明 单元综合测试(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览




文档简介
第一章综合提升卷
测试范围:三角形的证明 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.关于等腰三角形,有以下说法:
(1)有一个角为46°的等腰三角形一定是锐角三角形;
(2)等腰三角形两边的中线一定相等;
(3)两个等腰三角形,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等;
(4)等腰三角形两底角的平分线的交点到三边距离相等.
其中,正确说法的个数为
( )
A.1
B.2
C.3
D.4
2.用反证法证明命题:“如图1-Z-1,如果AB∥CD,AB∥EF,那么CD∥EF.”证明的第一步是
( )
图1-Z-1
A.假设CD∥EF
B.假设CD不平行于EF
C.已知AB∥EF
D.假设AB不平行于EF
3.已知下列命题:①若|x|=3,则x=3;②全等三角形的三组对应角相等;③直角三角形中30°角所对的直角边等于斜边的一半;④有理数与数轴上的点一一对应.其中原命题与逆命题均为真命题的个数是
( )
A.1
B.2
C.3
D.4
4.如图1-Z-2,若BD为等边三角形ABC的一条中线,延长BC至点E,使CE=CD=1,连接DE,则DE的长为
( )
图1-Z-2
A.
B.
C.
D.
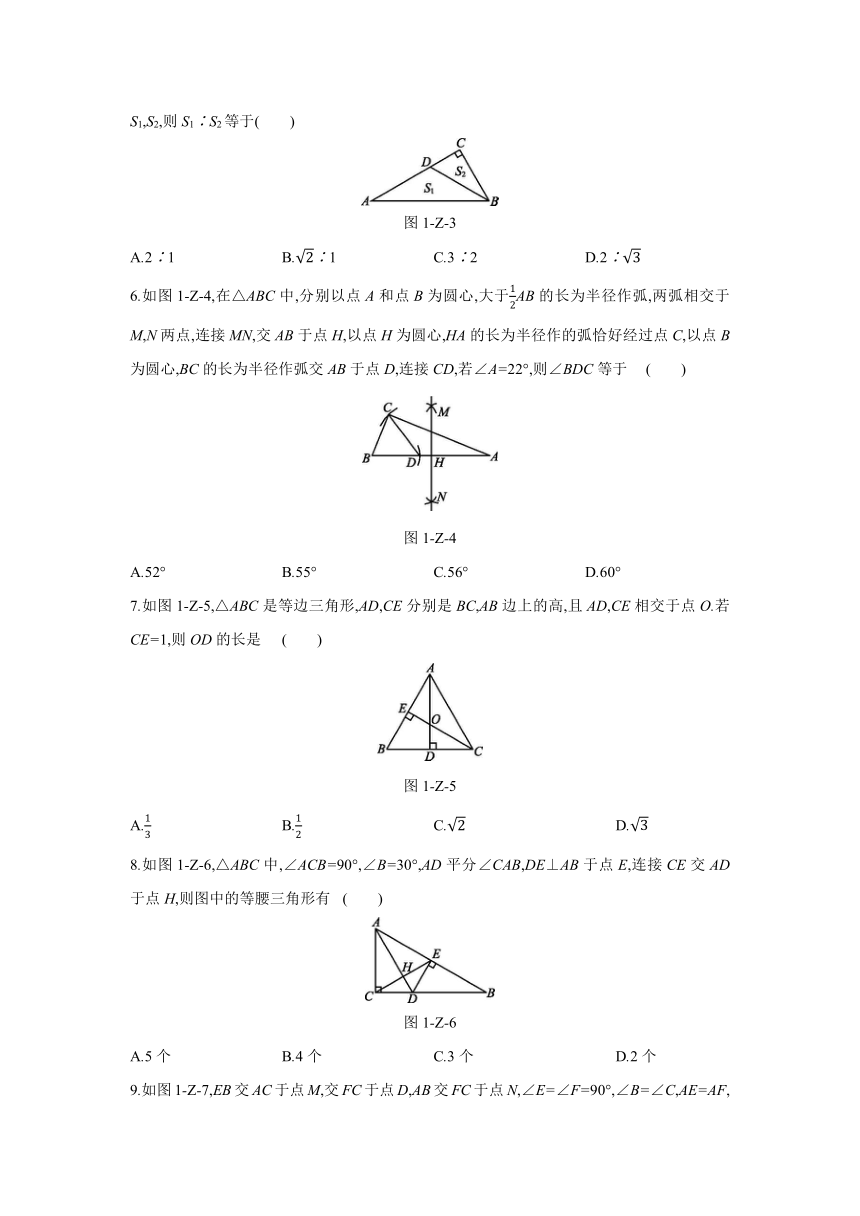
5.如图1-Z-3,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,设△ABD,△BCD的面积分别为S1,S2,则S1∶S2等于( )
图1-Z-3
A.2∶1
B.∶1
C.3∶2
D.2∶
6.如图1-Z-4,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC等于
( )
图1-Z-4
A.52°
B.55°
C.56°
D.60°
7.如图1-Z-5,△ABC是等边三角形,AD,CE分别是BC,AB边上的高,且AD,CE相交于点O.若CE=1,则OD的长是
( )
图1-Z-5
A.
B.
C.
D.
8.如图1-Z-6,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,DE⊥AB于点E,连接CE交AD于点H,则图中的等腰三角形有
( )
图1-Z-6
A.5个
B.4个
C.3个
D.2个
9.如图1-Z-7,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论中,正确的有
( )
图1-Z-7
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
10.如图1-Z-8,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在其右侧作等边三角形ACD,连接BD,则BD所在直线与OA所在直线的位置关系是
( )
图1-Z-8
A.平行
B.相交
C.垂直
D.平行、相交或垂直
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.命题“全等三角形的面积相等”的逆命题是 命题.(填“真”或“假”)?
12.如图1-Z-9,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 °.?
图1-Z-9
13.如图1-Z-10,有一张直角三角形纸片,两直角边AC=5
cm,BC=10
cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为 .?
图1-Z-10
图1-Z-11
14.如图1-Z-11,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F.如果BC=20
cm,那么DE+DF=
cm.?
15.如图1-Z-12,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则BF=
cm.?
图1-Z-12
图1-Z-13
16.如图1-Z-13,等边三角形ABC的边AB上有一点P,作PE⊥AC于点E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则有下列结论:①PD=DQ;②∠Q=30°;③DE=AC;④AE=CQ.其中正确的结论有 .(把所有正确结论的序号都写在横线上)?
三、解答题(共52分)
17.(5分)如图1-Z-14,已知等腰三角形ABC,顶角∠A=36°.
(1)在AC上作一点D,使AD=BD(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)求证:△BCD是等腰三角形.
图1-Z-14
18.(5分)如图1-Z-15,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,且∠A=30°,DE=1
cm.求△ABC的面积.(结果保留根号)
图1-Z-15
19.(6分)如图1-Z-16,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6
cm,请求出△BDE的周长.
图1-Z-16
20.(6分)如图1-Z-17,点P,M,N分别在等边三角形ABC的各边上,且MP⊥AB于点P,NM⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=12
cm,求MC的长.
图1-Z-17
21.(7分)如图1-Z-18,在四边形ABCD中,AB∥CD,∠ABC的平分线交CD的延长线于点E,F是BE的中点,连接CF并延长交AD于点G.
(1)求证:CG平分∠BCD;
(2)若∠ADE=110°,∠ABC=52°,求∠CGD的度数.
图1-Z-18
22.(7分)如图1-Z-19,在等腰三角形ABC中,AB=AC=8,∠BAC=100°,AD是△ABC的角平分线,DE∥AC交AB于点E.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
图1-Z-19
23.(8分)在△ABC中,∠BAC=120°,AB=AC,PC=PA,设∠APB=α,∠BPC=β.
(1)如图1-Z-20①,点P在△ABC内.
①若β=153°,求α的度数.
小明同学通过分析已知条件发现:△ABC是顶角为120°的等腰三角形,且PC=PA,从而容易联想到构造一个顶角为120°的等腰三角形.于是,他过点A作∠DAP=120°,且AD=AP,连接DP,DB,发现两个不同的三角形全等: ≌ ,再利用全等三角形及等腰三角形的相关知识可求出α的度数.?
请利用小明同学分析的思路,通过计算求得α的度数为 ;?
②小明在①的基础上进一步进行探索,发现α,β之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
(2)如图②,点P在△ABC外,那么a,β之间的数量关系是否改变?若改变,请直接写出它们之间的数量关系;若不变,请说明理由.
图1-Z-20
24.(8分)如图1-Z-21①,已知点B(0,9),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
(1)求证:DE=BO.
(2)如图②,当点D恰好落在BC上时,
①求点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,请说明理由.
③如图③,点M是线段BC上的动点(不与点B,C重合),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不发生变化,直接写出MH+MG的值;若发生变化,简要说明理由.
图1-Z-21
详解
1.B [解析]
(1)(4)正确.
2.B 3.A 4.B 5.A
6.C [解析]
如图,连接CH.
由题意得,直线MN是线段AB的垂直平分线,
∴AH=BH.
又∵CH=AH,
∴CH=AB,
∴∠ACB=90°.
∵∠A=22°,
∴∠ACH=∠A=22°,
∴∠BCH=∠B=68°.
∵BC=BD,
∴∠BDC=∠BCD=(180°-68°)=56°.
7.A 8.B
9.C [解析]
∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE≌△ACF(AAS),
∴BE=CF,故②正确,
∠BAE=∠CAF,
∴∠BAE-∠BAC=∠CAF-∠BAC,
即∠1=∠2,故①正确.
∵△ABE≌△ACF,
∴AB=AC.
又∵∠BAC=∠CAB,∠B=∠C,
∴△ACN≌△ABM(ASA),故③正确.
不能证明CD=DN成立,故④错误.
∵∠1=∠2,AF=AE,∠F=∠E,
∴△AFN≌△AEM(ASA),故⑤正确.
10.A [解析]
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠ABO=60°.
如图①,若点C在线段OB上,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD.
在△AOC和△ABD中,
∵OA=BA,∠OAC=∠BAD,AC=AD,
∴△AOC≌△ABD,∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA.
如图②,若点C在线段OB的延长线上,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD.
在△AOC和△ABD中,
∵OA=BA,∠OAC=∠BAD,AC=AD,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA.故选A.
11.假 12.34
13.
cm [解析]
设CD=x
cm,则BD=AD=(10-x)cm.在Rt△ACD中,由勾股定理,得(10-x)2=x2+52,解得x=.
14.10 [解析]
利用含30°角的直角三角形的性质得,DE+DF=(BD+CD)=BC.
15.6 [解析]
在Rt△ADB与Rt△ADC中,AB=AC,AD=AD,∴Rt△ADB≌Rt△ADC,
∴S△ABC=2S△ABD=2×AB·DE=AB·DE=3AB.∵S△ABC=AC·BF,∴AC·BF=3AB.∵AC=AB,∴BF=3,∴BF=6(cm).
16.①③④ [解析]
①过点P作PF∥BQ,交AC于点F.
∵△ABC是等边三角形,∴∠ACB=∠A=60°.
∵PF∥BQ,
∴∠AFP=∠ACB=60°,∠PFD=∠QCD,
∴△AFP是等边三角形,
∴PF=PA.
∵PA=CQ,∴PF=CQ.
在△PFD和△QCD中,
∵∠FDP=∠CDQ,∠PFD=∠QCD,PF=CQ,
∴△PFD≌△QCD,
∴PD=DQ,故①正确.
②∵△PFD≌△QCD,
∴∠DPF=∠Q.
∵△APF为等边三角形,
∴∠APF=60°.
∵QP与AB不一定垂直,
∴∠Q不一定为30°,故②不正确.
③∵△APF是等边三角形,PE⊥AC,
∴EF=AF.
∵△PFD≌△QCD,∴DF=DC,∴DF=FC,∴DE=EF+DF=AF+FC=AC,故③正确.
④在Rt△AEP中,∠A=60°,∴∠APE=30°,∴AE=AP,∴AE=CQ,故④正确.
则本题正确的结论有①③④.
17.解:(1)如图,点D为所作.
(2)证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°-36°)=72°.
∵AD=BD,∴∠ABD=∠A=36°,
∴∠BDC=∠A+∠ABD=36°+36°=72°,
∴∠BDC=∠C,∴BD=BC,
∴△BCD是等腰三角形.
18.解:∵DE垂直平分AB,∠A=30°,DE=1
cm,
∴AE=2
cm,
∴AD==(cm),
∴AB=2AD=2
cm.
在Rt△ABC中,∠A=30°,
∴BC=AB=
cm,
∴AC==3(cm),
∴S△ABC=××3=
(cm2).
19.解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DE=DC.
在Rt△ADC和Rt△ADE中,
∵DC=DE,AD=AD,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE.
又∵AC=BC,∴AE=BC,
∴△BDE的周长=DE+DB+EB=BC+EB=AE+EB=AB.
∵AB=6
cm,∴△BDE的周长为6
cm.
20.解:(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵MP⊥AB,NM⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形.
(2)∵△PMN是等边三角形,
∴PN=PM=NM.
又∵∠A=∠B=∠C,∠PNA=∠MPB=∠NMC,∴△PBM≌△MCN≌△NAP,
∴PA=BM=CN,PB=MC=AN,
∴BM+PB=AB=12
cm.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,∴2PB+PB=12
cm,
∴PB=4
cm,∴MC=4
cm.
21.解:(1)证明:∵BE平分∠ABC,
∴∠ABF=∠CBF=∠ABC.
∵AB∥CD,
∴∠ABF=∠E,
∴∠CBF=∠E,
∴BC=CE,
∴△BCE是等腰三角形.
∵F为BE的中点,
∴CF平分∠BCD,
即CG平分∠BCD.
(2)∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵∠ABC=52°,
∴∠BCD=128°.
∵CG平分∠BCD,
∴∠GCD=∠BCD=64°.
∵∠ADE=110°,∠ADE=∠CGD+∠GCD,
∴∠CGD=46°.
22.解:(1)∵∠BAC=100°,且AD平分∠BAC,
∴∠BAD=50°.
(2)在等腰三角形ABC中,∠B==40°.
(3)∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE.
∵DE∥AC,
∴∠EDB=∠C.
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,
∴BE=DE,
∴DE=BE=AE=AB=×8=4.
23.解:(1)①△ADB △APC 63°
②β-α=90°.
证明:如图①,过点A作AH⊥DP于点H.
∵∠DAP=∠BAC=120°,
∴∠DAB=∠PAC,且AD=AP,AB=AC,
∴△ADB≌△APC(SAS),
∴BD=PC=PA,∠ADB=∠APC.
∵∠DAP=120°,AD=AP,AH⊥DP,
∴∠ADP=∠APD=30°,DH=PH,
∴AP=2AH,HP=AH,
∴DP=AP,∴BD=DP,
∴∠DBP=∠DPB=∠APB-∠APD=α-30°,
∴∠BDP=180°-2(α-30°)=240°-2α,
∴∠ADB=∠BDP+∠ADP=270°-2α=∠APC.
∵∠APB+∠APC+∠BPC=360°,
∴270°-2α+α+β=360°,∴β-α=90°.
(2)α,β之间的数量关系改变了,α+β=90°.
理由如下:如图②,作∠PAN=120°,且PA=NA,连接PN,BN.
∵∠PAN=∠BAC=120°,
∴∠BAN=∠PAC.
又∵AB=AC,NA=PA,
∴△ABN≌△ACP(SAS),
∴∠BNA=∠APC,
PC=BN=AP.
∵∠PAN=120°,PA=NA,
∴∠APN=∠ANP=30°,
∴PN=PA=BN,
∴∠BPN=∠PBN=α+30°.
∵∠BPN+∠PBN+∠BNP=180°,
∴2(α+30°)+β-α+30°=180°,
∴α+β=90°.
24.解:(1)证明:∵△ODC和△EBC都是等边三角形,
∴OC=DC,BC=CE,∠OCD=∠BCE=60°,
∴∠BCE+∠BCD=∠OCD+∠BCD,
即∠ECD=∠BCO,
∴△DEC≌△OBC(SAS),
∴DE=BO.
(2)①∵△ODC是等边三角形,
∴∠OCB=60°.
∵∠BOC=90°,
∴∠OBC=30°.
设OC=x,则BC=2x,
∴x2+92=(2x)2,解得x=3,
∴BC=6.
∵△EBC是等边三角形,
∴BE=BC=6,∠CBE=60°,
∴∠OBE=∠OBC+∠CBE=90°,BE∥轴,
∴E(6,9).
②存在.当CP=CE=6时,△PEC是等腰三角形.
∵C(3,0),
∴点P的坐标为(-3,0)或(9,0).
③MH+MG的值不发生变化.如图,连接EM.
由(1)知△DEC≌△OBC,∴DE=BO=9,∠EDC=∠BOC=90°,即ED⊥BC.
∵S△EBC=S△EBM+S△ECM,MG⊥BE,MH⊥EC,
∴BC·DE=BE·MG+EC·MH.
∵BE=BC=EC,∴MG+MH=DE=9.
测试范围:三角形的证明 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.关于等腰三角形,有以下说法:
(1)有一个角为46°的等腰三角形一定是锐角三角形;
(2)等腰三角形两边的中线一定相等;
(3)两个等腰三角形,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等;
(4)等腰三角形两底角的平分线的交点到三边距离相等.
其中,正确说法的个数为
( )
A.1
B.2
C.3
D.4
2.用反证法证明命题:“如图1-Z-1,如果AB∥CD,AB∥EF,那么CD∥EF.”证明的第一步是
( )
图1-Z-1
A.假设CD∥EF
B.假设CD不平行于EF
C.已知AB∥EF
D.假设AB不平行于EF
3.已知下列命题:①若|x|=3,则x=3;②全等三角形的三组对应角相等;③直角三角形中30°角所对的直角边等于斜边的一半;④有理数与数轴上的点一一对应.其中原命题与逆命题均为真命题的个数是
( )
A.1
B.2
C.3
D.4
4.如图1-Z-2,若BD为等边三角形ABC的一条中线,延长BC至点E,使CE=CD=1,连接DE,则DE的长为
( )
图1-Z-2
A.
B.
C.
D.
5.如图1-Z-3,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,设△ABD,△BCD的面积分别为S1,S2,则S1∶S2等于( )
图1-Z-3
A.2∶1
B.∶1
C.3∶2
D.2∶
6.如图1-Z-4,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC等于
( )
图1-Z-4
A.52°
B.55°
C.56°
D.60°
7.如图1-Z-5,△ABC是等边三角形,AD,CE分别是BC,AB边上的高,且AD,CE相交于点O.若CE=1,则OD的长是
( )
图1-Z-5
A.
B.
C.
D.
8.如图1-Z-6,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,DE⊥AB于点E,连接CE交AD于点H,则图中的等腰三角形有
( )
图1-Z-6
A.5个
B.4个
C.3个
D.2个
9.如图1-Z-7,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论中,正确的有
( )
图1-Z-7
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
10.如图1-Z-8,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在其右侧作等边三角形ACD,连接BD,则BD所在直线与OA所在直线的位置关系是
( )
图1-Z-8
A.平行
B.相交
C.垂直
D.平行、相交或垂直
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.命题“全等三角形的面积相等”的逆命题是 命题.(填“真”或“假”)?
12.如图1-Z-9,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 °.?
图1-Z-9
13.如图1-Z-10,有一张直角三角形纸片,两直角边AC=5
cm,BC=10
cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为 .?
图1-Z-10
图1-Z-11
14.如图1-Z-11,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F.如果BC=20
cm,那么DE+DF=
cm.?
15.如图1-Z-12,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则BF=
cm.?
图1-Z-12
图1-Z-13
16.如图1-Z-13,等边三角形ABC的边AB上有一点P,作PE⊥AC于点E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则有下列结论:①PD=DQ;②∠Q=30°;③DE=AC;④AE=CQ.其中正确的结论有 .(把所有正确结论的序号都写在横线上)?
三、解答题(共52分)
17.(5分)如图1-Z-14,已知等腰三角形ABC,顶角∠A=36°.
(1)在AC上作一点D,使AD=BD(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)求证:△BCD是等腰三角形.
图1-Z-14
18.(5分)如图1-Z-15,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,且∠A=30°,DE=1
cm.求△ABC的面积.(结果保留根号)
图1-Z-15
19.(6分)如图1-Z-16,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6
cm,请求出△BDE的周长.
图1-Z-16
20.(6分)如图1-Z-17,点P,M,N分别在等边三角形ABC的各边上,且MP⊥AB于点P,NM⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=12
cm,求MC的长.
图1-Z-17
21.(7分)如图1-Z-18,在四边形ABCD中,AB∥CD,∠ABC的平分线交CD的延长线于点E,F是BE的中点,连接CF并延长交AD于点G.
(1)求证:CG平分∠BCD;
(2)若∠ADE=110°,∠ABC=52°,求∠CGD的度数.
图1-Z-18
22.(7分)如图1-Z-19,在等腰三角形ABC中,AB=AC=8,∠BAC=100°,AD是△ABC的角平分线,DE∥AC交AB于点E.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
图1-Z-19
23.(8分)在△ABC中,∠BAC=120°,AB=AC,PC=PA,设∠APB=α,∠BPC=β.
(1)如图1-Z-20①,点P在△ABC内.
①若β=153°,求α的度数.
小明同学通过分析已知条件发现:△ABC是顶角为120°的等腰三角形,且PC=PA,从而容易联想到构造一个顶角为120°的等腰三角形.于是,他过点A作∠DAP=120°,且AD=AP,连接DP,DB,发现两个不同的三角形全等: ≌ ,再利用全等三角形及等腰三角形的相关知识可求出α的度数.?
请利用小明同学分析的思路,通过计算求得α的度数为 ;?
②小明在①的基础上进一步进行探索,发现α,β之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
(2)如图②,点P在△ABC外,那么a,β之间的数量关系是否改变?若改变,请直接写出它们之间的数量关系;若不变,请说明理由.
图1-Z-20
24.(8分)如图1-Z-21①,已知点B(0,9),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
(1)求证:DE=BO.
(2)如图②,当点D恰好落在BC上时,
①求点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,请说明理由.
③如图③,点M是线段BC上的动点(不与点B,C重合),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不发生变化,直接写出MH+MG的值;若发生变化,简要说明理由.
图1-Z-21
详解
1.B [解析]
(1)(4)正确.
2.B 3.A 4.B 5.A
6.C [解析]
如图,连接CH.
由题意得,直线MN是线段AB的垂直平分线,
∴AH=BH.
又∵CH=AH,
∴CH=AB,
∴∠ACB=90°.
∵∠A=22°,
∴∠ACH=∠A=22°,
∴∠BCH=∠B=68°.
∵BC=BD,
∴∠BDC=∠BCD=(180°-68°)=56°.
7.A 8.B
9.C [解析]
∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE≌△ACF(AAS),
∴BE=CF,故②正确,
∠BAE=∠CAF,
∴∠BAE-∠BAC=∠CAF-∠BAC,
即∠1=∠2,故①正确.
∵△ABE≌△ACF,
∴AB=AC.
又∵∠BAC=∠CAB,∠B=∠C,
∴△ACN≌△ABM(ASA),故③正确.
不能证明CD=DN成立,故④错误.
∵∠1=∠2,AF=AE,∠F=∠E,
∴△AFN≌△AEM(ASA),故⑤正确.
10.A [解析]
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠ABO=60°.
如图①,若点C在线段OB上,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD.
在△AOC和△ABD中,
∵OA=BA,∠OAC=∠BAD,AC=AD,
∴△AOC≌△ABD,∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA.
如图②,若点C在线段OB的延长线上,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD.
在△AOC和△ABD中,
∵OA=BA,∠OAC=∠BAD,AC=AD,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD∥OA.故选A.
11.假 12.34
13.
cm [解析]
设CD=x
cm,则BD=AD=(10-x)cm.在Rt△ACD中,由勾股定理,得(10-x)2=x2+52,解得x=.
14.10 [解析]
利用含30°角的直角三角形的性质得,DE+DF=(BD+CD)=BC.
15.6 [解析]
在Rt△ADB与Rt△ADC中,AB=AC,AD=AD,∴Rt△ADB≌Rt△ADC,
∴S△ABC=2S△ABD=2×AB·DE=AB·DE=3AB.∵S△ABC=AC·BF,∴AC·BF=3AB.∵AC=AB,∴BF=3,∴BF=6(cm).
16.①③④ [解析]
①过点P作PF∥BQ,交AC于点F.
∵△ABC是等边三角形,∴∠ACB=∠A=60°.
∵PF∥BQ,
∴∠AFP=∠ACB=60°,∠PFD=∠QCD,
∴△AFP是等边三角形,
∴PF=PA.
∵PA=CQ,∴PF=CQ.
在△PFD和△QCD中,
∵∠FDP=∠CDQ,∠PFD=∠QCD,PF=CQ,
∴△PFD≌△QCD,
∴PD=DQ,故①正确.
②∵△PFD≌△QCD,
∴∠DPF=∠Q.
∵△APF为等边三角形,
∴∠APF=60°.
∵QP与AB不一定垂直,
∴∠Q不一定为30°,故②不正确.
③∵△APF是等边三角形,PE⊥AC,
∴EF=AF.
∵△PFD≌△QCD,∴DF=DC,∴DF=FC,∴DE=EF+DF=AF+FC=AC,故③正确.
④在Rt△AEP中,∠A=60°,∴∠APE=30°,∴AE=AP,∴AE=CQ,故④正确.
则本题正确的结论有①③④.
17.解:(1)如图,点D为所作.
(2)证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°-36°)=72°.
∵AD=BD,∴∠ABD=∠A=36°,
∴∠BDC=∠A+∠ABD=36°+36°=72°,
∴∠BDC=∠C,∴BD=BC,
∴△BCD是等腰三角形.
18.解:∵DE垂直平分AB,∠A=30°,DE=1
cm,
∴AE=2
cm,
∴AD==(cm),
∴AB=2AD=2
cm.
在Rt△ABC中,∠A=30°,
∴BC=AB=
cm,
∴AC==3(cm),
∴S△ABC=××3=
(cm2).
19.解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DE=DC.
在Rt△ADC和Rt△ADE中,
∵DC=DE,AD=AD,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE.
又∵AC=BC,∴AE=BC,
∴△BDE的周长=DE+DB+EB=BC+EB=AE+EB=AB.
∵AB=6
cm,∴△BDE的周长为6
cm.
20.解:(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵MP⊥AB,NM⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形.
(2)∵△PMN是等边三角形,
∴PN=PM=NM.
又∵∠A=∠B=∠C,∠PNA=∠MPB=∠NMC,∴△PBM≌△MCN≌△NAP,
∴PA=BM=CN,PB=MC=AN,
∴BM+PB=AB=12
cm.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,∴2PB+PB=12
cm,
∴PB=4
cm,∴MC=4
cm.
21.解:(1)证明:∵BE平分∠ABC,
∴∠ABF=∠CBF=∠ABC.
∵AB∥CD,
∴∠ABF=∠E,
∴∠CBF=∠E,
∴BC=CE,
∴△BCE是等腰三角形.
∵F为BE的中点,
∴CF平分∠BCD,
即CG平分∠BCD.
(2)∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵∠ABC=52°,
∴∠BCD=128°.
∵CG平分∠BCD,
∴∠GCD=∠BCD=64°.
∵∠ADE=110°,∠ADE=∠CGD+∠GCD,
∴∠CGD=46°.
22.解:(1)∵∠BAC=100°,且AD平分∠BAC,
∴∠BAD=50°.
(2)在等腰三角形ABC中,∠B==40°.
(3)∵AD平分∠BAC,
∴∠EAD=∠CAD.
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠EAD=∠ADE,
∴AE=DE.
∵DE∥AC,
∴∠EDB=∠C.
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,
∴BE=DE,
∴DE=BE=AE=AB=×8=4.
23.解:(1)①△ADB △APC 63°
②β-α=90°.
证明:如图①,过点A作AH⊥DP于点H.
∵∠DAP=∠BAC=120°,
∴∠DAB=∠PAC,且AD=AP,AB=AC,
∴△ADB≌△APC(SAS),
∴BD=PC=PA,∠ADB=∠APC.
∵∠DAP=120°,AD=AP,AH⊥DP,
∴∠ADP=∠APD=30°,DH=PH,
∴AP=2AH,HP=AH,
∴DP=AP,∴BD=DP,
∴∠DBP=∠DPB=∠APB-∠APD=α-30°,
∴∠BDP=180°-2(α-30°)=240°-2α,
∴∠ADB=∠BDP+∠ADP=270°-2α=∠APC.
∵∠APB+∠APC+∠BPC=360°,
∴270°-2α+α+β=360°,∴β-α=90°.
(2)α,β之间的数量关系改变了,α+β=90°.
理由如下:如图②,作∠PAN=120°,且PA=NA,连接PN,BN.
∵∠PAN=∠BAC=120°,
∴∠BAN=∠PAC.
又∵AB=AC,NA=PA,
∴△ABN≌△ACP(SAS),
∴∠BNA=∠APC,
PC=BN=AP.
∵∠PAN=120°,PA=NA,
∴∠APN=∠ANP=30°,
∴PN=PA=BN,
∴∠BPN=∠PBN=α+30°.
∵∠BPN+∠PBN+∠BNP=180°,
∴2(α+30°)+β-α+30°=180°,
∴α+β=90°.
24.解:(1)证明:∵△ODC和△EBC都是等边三角形,
∴OC=DC,BC=CE,∠OCD=∠BCE=60°,
∴∠BCE+∠BCD=∠OCD+∠BCD,
即∠ECD=∠BCO,
∴△DEC≌△OBC(SAS),
∴DE=BO.
(2)①∵△ODC是等边三角形,
∴∠OCB=60°.
∵∠BOC=90°,
∴∠OBC=30°.
设OC=x,则BC=2x,
∴x2+92=(2x)2,解得x=3,
∴BC=6.
∵△EBC是等边三角形,
∴BE=BC=6,∠CBE=60°,
∴∠OBE=∠OBC+∠CBE=90°,BE∥轴,
∴E(6,9).
②存在.当CP=CE=6时,△PEC是等腰三角形.
∵C(3,0),
∴点P的坐标为(-3,0)或(9,0).
③MH+MG的值不发生变化.如图,连接EM.
由(1)知△DEC≌△OBC,∴DE=BO=9,∠EDC=∠BOC=90°,即ED⊥BC.
∵S△EBC=S△EBM+S△ECM,MG⊥BE,MH⊥EC,
∴BC·DE=BE·MG+EC·MH.
∵BE=BC=EC,∴MG+MH=DE=9.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
