2020-2021学年七年级数学人教版下册同步练习5.1相交线 练习卷(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册同步练习5.1相交线 练习卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 22:55:28 | ||
图片预览




文档简介
新人教版七年级数学下册同步练习
5.1相交线
一.选择题(共10小题,每小题3分,满分30分)
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3
B.0、1或3
C.0、1或2
D.0、1、2或3
2.下列各组角中,∠1与∠2是对顶角的为( )
A.
B.
C.
D.
3.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
A.20°
B.160°
C.20°或160°
D.70°
4.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是( )
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
5.如图,能表示点到直线的距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
6.如图,与∠1是同旁内角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
7.已知点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.2cm
B.小于2cm
C.不大于2cm
D.以上答案均不对
8.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )
A.35°
B.45°
C.55°
D.65°
9.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
10.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm
二.填空题(共6小题,每小题3分,满分18分)
11.如图,一条直线l1,最多将平面分成两块,两条直线l1,l2相交,最多将平面分成4块,三条直线l1,l2,l3最多将平面分成7块,…,则9条直线l1,l2,…l9最多将平面分成
块.
12.如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠COE=65°,则∠BOD=
°.
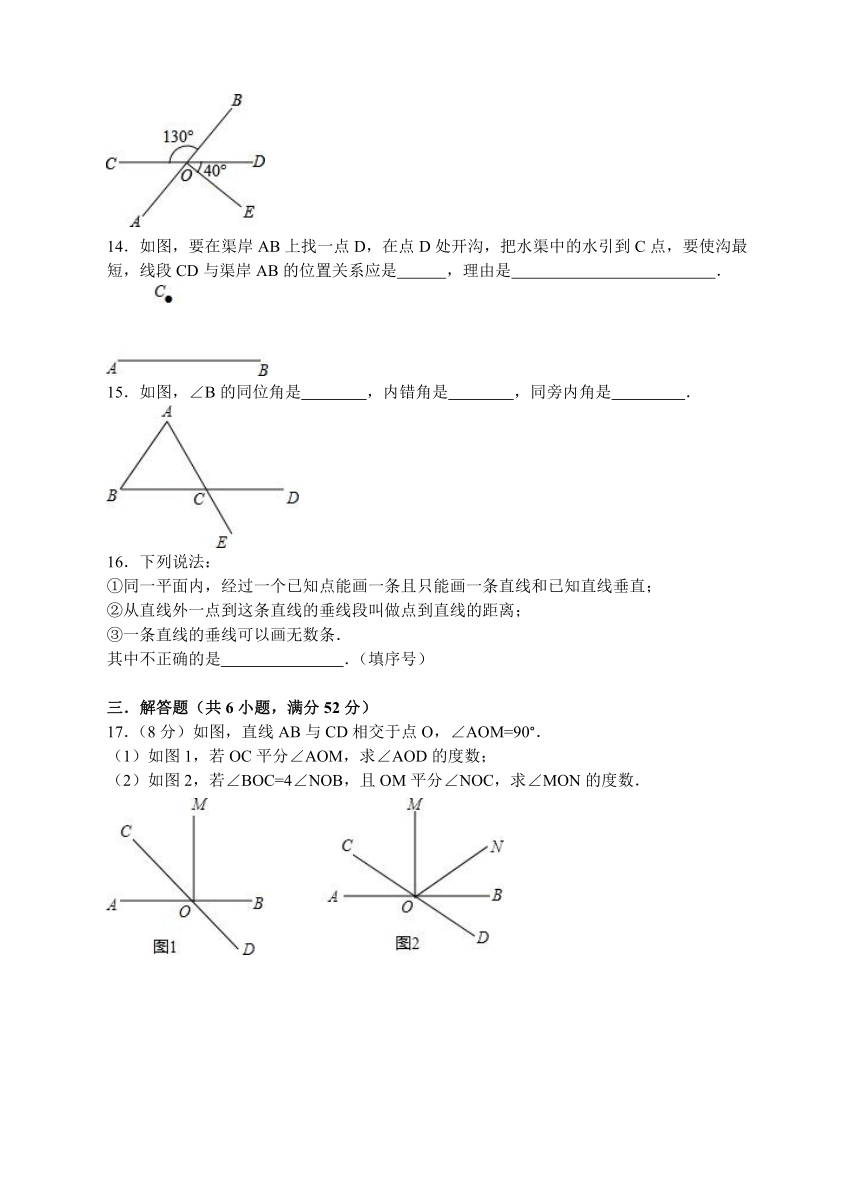
13.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是
.
14.如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是
,理由是
.
15.如图,∠B的同位角是
,内错角是
,同旁内角是
.
16.下列说法:
①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直;
②从直线外一点到这条直线的垂线段叫做点到直线的距离;
③一条直线的垂线可以画无数条.
其中不正确的是
.(填序号)
三.解答题(共6小题,满分52分)
17.(8分)如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
18.(8分)如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数.
(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.
19.(8分)如图,在三角形△ABC中,∠BCA=90°,BC=3,AC=4,AB=5.点P是线段AB上的一动点,求线段CP的最小值是多少?
20.(8分)如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?
21.(10分)说出下列各对角分别是哪一条直线截哪两条直线形成什么角?
(1)∠A和∠ACG
(2)∠ACF和∠CED
(3)∠AED和∠ACB
(4)∠B和∠BCG.
22.(10分)已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
新人教版七年级数学下册同步练习
5.1相交线
参考答案与试题解析
选择题(共10小题,每小题3分,满分30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
C
D
D
C
C
B
C
解析:
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3
B.0、1或3
C.0、1或2
D.0、1、2或3
选D.
2.下列各组角中,∠1与∠2是对顶角的为( )
A.
B.
C.
D.
解:根据两条直线相交,才能构成对顶角进行判断,
A、B、C都不是由两条直线相交构成的图形,错误;
D是由两条直线相交构成的图形,正确.
故选D.
3.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
A.20°
B.160°
C.20°或160°
D.70°
解:∵β的两边与α的两边分别垂直,
∴α+β=180°,
故β=160°,
在上述情况下,若反向延长∠β的一边,那么∠β的补角的两边也与∠α的两边互相垂直,故此时∠β=180°﹣20°=160°;
综上可知:∠β=20°或160°,
故选:C.
4.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是( )
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故选:C.
5.如图,能表示点到直线的距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
解:根据点到直线的距离定义,可判断:
AB表示点A到直线BC的距离;
AD表示点A到直线BD的距离;
BD表示点B到直线AC的距离;
CB表示点C到直线AB的距离;
CD表示点C到直线BD的距离.
共5条.故选D.
6.如图,与∠1是同旁内角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
解:A、∠1和∠2是对顶角,不是同旁内角,故本选项错误;
B、∠1和∠3是同位角,不是同旁内角,故本选项错误;
C、∠1和∠4是内错角,不是同旁内角,故本选项错误;
D、∠1和∠5是同旁内角,故本选项正确;
故选D.
7.已知点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.2cm
B.小于2cm
C.不大于2cm
D.以上答案均不对
解:∵垂线段最短,
又∵点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,
∴点P到直线m的距离小于或等于2cm,即不大于2cm,
故选C.
8.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )
A.35°
B.45°
C.55°
D.65°
解:∵∠B0C=∠AOD=70°,
又∵OE平分∠BOC,
∴∠BOE=∠BOC=35°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选C.
9.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
解:(1)同位角只是一种位置关系,只有两条直线平行时,同位角相等,错误;
(2)强调了在平面内,正确;
(3)不符合对顶角的定义,错误;
(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段的本身,而是指垂线段的长度.
故选:B.
10.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm
解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PC,
即点P到直线l的距离不大于4.
故选C.
二.填空题(共6小题,每小题3分,满分18分)
11.如图,一条直线l1,最多将平面分成两块,两条直线l1,l2相交,最多将平面分成4块,三条直线l1,l2,l3最多将平面分成7块,…,则9条直线l1,l2,…l9最多将平面分成 46 块.
解:∵n=1,f(1)=1+1=2,
n=2,f(2)=f(1)+2=4,
n=3,f(3)=f(2)+3=7,
n=4,f(4)=f(3)+4=11,
n=5,f(5)=f(4)+5=16,
n=6,f(5)=f(5)+6=22,
n=7,f(7)=f(6)+7=29,
n=8,f(8)=f(7)+8=37,
n=9,f(9)=f(8)+9=46,
故答案为:46.
12.如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠COE=65°,则∠BOD= 50 °.
解:∵OE平分∠BOC,
∴∠BOC=2∠COE=65°×2=130°,
∴∠AOC=180°﹣130°=50°,
∴∠BOD=50°,
故答案为:50.
13.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是 垂直 .
解:∵∠BOC=130°,
∴∠AOD=∠BOC=130°,
∴∠AOE=∠AOD﹣∠EOD=130°﹣40°=90°.
∴OE⊥AB.
故空中填:互相垂直.
14.如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是 垂直 ,理由是 垂线段最短 .
解:要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是
垂直,理由是
垂线段最短,
故答案为:垂直,垂线段最短.
15.如图,∠B的同位角是 ∠ACD ,内错角是 ∠BCE ,同旁内角是 ∠BAC和∠ACB .
解:∠B的同位角是∠ACD,内错角是∠BCE,同旁内角是∠BAC和∠ACB,
故答案为:∠ACD;∠BCE;∠BAC和∠ACB
16.下列说法:
①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直;
②从直线外一点到这条直线的垂线段叫做点到直线的距离;
③一条直线的垂线可以画无数条.
其中不正确的是 ② .(填序号)
解:①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直,故①正确;
②从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故②错误;
③一条直线的垂线可以画无数条,故③正确;
故答案为:②.
三.解答题(共6小题,满分52分)
17.(8分)如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=∠AOM=×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=∠CON=x°,
∵∠BOM=x+x=90°,
∴x=36°,
∴∠MON=x°=×36°=54°,
即∠MON的度数为54°.
18.(8分)如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数.
(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.
解:(1)∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°,
∴∠AOC=70°,∠AOD=110°,
∵∠BOD=∠AOC,
∴∠BOD=70°,
∵OE平分∠BOD,
∴∠DOE=35°,
∴∠COE=180°﹣∠DOE=145°;
(2)分两种情况,
如图1,∵OF⊥OE,
∴∠EOF=90°,
∴∠COF=∠COE﹣∠EOF=145°﹣90°=55°,
如图2,∠COF=∠360°﹣∠COE﹣∠EOF=125°.
19.(8分)如图,在三角形△ABC中,∠BCA=90°,BC=3,AC=4,AB=5.点P是线段AB上的一动点,求线段CP的最小值是多少?
解:当CP垂直AB时有最小值,
因为:∠BCA=90°,BC=3,AC=4,AB=5,
∴S△ABC=BC?AC=AB?CP,
即×3×4=×5CP,
解得CP=2.4,
答:CP的最小值是2.4.
20.(8分)如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?
解:点B在点A北偏东35°方向,点C在点B北偏西55°方向,
∴∠CBA=90°,
点C到直线AB的距离是BC的长,
∵BC=10m,
∴点C到直线AB的距离是10m.
21.(10分)说出下列各对角分别是哪一条直线截哪两条直线形成什么角?
(1)∠A和∠ACG
(2)∠ACF和∠CED
(3)∠AED和∠ACB
(4)∠B和∠BCG.
解:(1)∠A和∠ACG是直线AC截直线CG、AB形成的内错角;
(2)∠ACF和∠CED是直线AC截直线FB、ED形成的内错角;
(3)∠AED和∠ACB是直线AC截直线DE、FB形成的同位角;
(4)∠B和∠BCG是直线FB截直线CG、AB形成的同旁内角;
22.(10分)已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
(1)解:∵当AC⊥直线a时,A为垂足,此时d=AC=2厘米,
∴0<d≤2;
(2)解:如图所示:
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
5.1相交线
一.选择题(共10小题,每小题3分,满分30分)
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3
B.0、1或3
C.0、1或2
D.0、1、2或3
2.下列各组角中,∠1与∠2是对顶角的为( )
A.
B.
C.
D.
3.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
A.20°
B.160°
C.20°或160°
D.70°
4.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是( )
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
5.如图,能表示点到直线的距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
6.如图,与∠1是同旁内角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
7.已知点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.2cm
B.小于2cm
C.不大于2cm
D.以上答案均不对
8.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )
A.35°
B.45°
C.55°
D.65°
9.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
10.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm
二.填空题(共6小题,每小题3分,满分18分)
11.如图,一条直线l1,最多将平面分成两块,两条直线l1,l2相交,最多将平面分成4块,三条直线l1,l2,l3最多将平面分成7块,…,则9条直线l1,l2,…l9最多将平面分成
块.
12.如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠COE=65°,则∠BOD=
°.
13.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是
.
14.如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是
,理由是
.
15.如图,∠B的同位角是
,内错角是
,同旁内角是
.
16.下列说法:
①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直;
②从直线外一点到这条直线的垂线段叫做点到直线的距离;
③一条直线的垂线可以画无数条.
其中不正确的是
.(填序号)
三.解答题(共6小题,满分52分)
17.(8分)如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
18.(8分)如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数.
(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.
19.(8分)如图,在三角形△ABC中,∠BCA=90°,BC=3,AC=4,AB=5.点P是线段AB上的一动点,求线段CP的最小值是多少?
20.(8分)如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?
21.(10分)说出下列各对角分别是哪一条直线截哪两条直线形成什么角?
(1)∠A和∠ACG
(2)∠ACF和∠CED
(3)∠AED和∠ACB
(4)∠B和∠BCG.
22.(10分)已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
新人教版七年级数学下册同步练习
5.1相交线
参考答案与试题解析
选择题(共10小题,每小题3分,满分30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
C
D
D
C
C
B
C
解析:
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3
B.0、1或3
C.0、1或2
D.0、1、2或3
选D.
2.下列各组角中,∠1与∠2是对顶角的为( )
A.
B.
C.
D.
解:根据两条直线相交,才能构成对顶角进行判断,
A、B、C都不是由两条直线相交构成的图形,错误;
D是由两条直线相交构成的图形,正确.
故选D.
3.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
A.20°
B.160°
C.20°或160°
D.70°
解:∵β的两边与α的两边分别垂直,
∴α+β=180°,
故β=160°,
在上述情况下,若反向延长∠β的一边,那么∠β的补角的两边也与∠α的两边互相垂直,故此时∠β=180°﹣20°=160°;
综上可知:∠β=20°或160°,
故选:C.
4.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是( )
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故选:C.
5.如图,能表示点到直线的距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
解:根据点到直线的距离定义,可判断:
AB表示点A到直线BC的距离;
AD表示点A到直线BD的距离;
BD表示点B到直线AC的距离;
CB表示点C到直线AB的距离;
CD表示点C到直线BD的距离.
共5条.故选D.
6.如图,与∠1是同旁内角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
解:A、∠1和∠2是对顶角,不是同旁内角,故本选项错误;
B、∠1和∠3是同位角,不是同旁内角,故本选项错误;
C、∠1和∠4是内错角,不是同旁内角,故本选项错误;
D、∠1和∠5是同旁内角,故本选项正确;
故选D.
7.已知点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.2cm
B.小于2cm
C.不大于2cm
D.以上答案均不对
解:∵垂线段最短,
又∵点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,
∴点P到直线m的距离小于或等于2cm,即不大于2cm,
故选C.
8.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )
A.35°
B.45°
C.55°
D.65°
解:∵∠B0C=∠AOD=70°,
又∵OE平分∠BOC,
∴∠BOE=∠BOC=35°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选C.
9.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
解:(1)同位角只是一种位置关系,只有两条直线平行时,同位角相等,错误;
(2)强调了在平面内,正确;
(3)不符合对顶角的定义,错误;
(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段的本身,而是指垂线段的长度.
故选:B.
10.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm
解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PC,
即点P到直线l的距离不大于4.
故选C.
二.填空题(共6小题,每小题3分,满分18分)
11.如图,一条直线l1,最多将平面分成两块,两条直线l1,l2相交,最多将平面分成4块,三条直线l1,l2,l3最多将平面分成7块,…,则9条直线l1,l2,…l9最多将平面分成 46 块.
解:∵n=1,f(1)=1+1=2,
n=2,f(2)=f(1)+2=4,
n=3,f(3)=f(2)+3=7,
n=4,f(4)=f(3)+4=11,
n=5,f(5)=f(4)+5=16,
n=6,f(5)=f(5)+6=22,
n=7,f(7)=f(6)+7=29,
n=8,f(8)=f(7)+8=37,
n=9,f(9)=f(8)+9=46,
故答案为:46.
12.如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠COE=65°,则∠BOD= 50 °.
解:∵OE平分∠BOC,
∴∠BOC=2∠COE=65°×2=130°,
∴∠AOC=180°﹣130°=50°,
∴∠BOD=50°,
故答案为:50.
13.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是 垂直 .
解:∵∠BOC=130°,
∴∠AOD=∠BOC=130°,
∴∠AOE=∠AOD﹣∠EOD=130°﹣40°=90°.
∴OE⊥AB.
故空中填:互相垂直.
14.如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是 垂直 ,理由是 垂线段最短 .
解:要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是
垂直,理由是
垂线段最短,
故答案为:垂直,垂线段最短.
15.如图,∠B的同位角是 ∠ACD ,内错角是 ∠BCE ,同旁内角是 ∠BAC和∠ACB .
解:∠B的同位角是∠ACD,内错角是∠BCE,同旁内角是∠BAC和∠ACB,
故答案为:∠ACD;∠BCE;∠BAC和∠ACB
16.下列说法:
①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直;
②从直线外一点到这条直线的垂线段叫做点到直线的距离;
③一条直线的垂线可以画无数条.
其中不正确的是 ② .(填序号)
解:①同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直,故①正确;
②从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故②错误;
③一条直线的垂线可以画无数条,故③正确;
故答案为:②.
三.解答题(共6小题,满分52分)
17.(8分)如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=∠AOM=×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=∠CON=x°,
∵∠BOM=x+x=90°,
∴x=36°,
∴∠MON=x°=×36°=54°,
即∠MON的度数为54°.
18.(8分)如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数.
(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.
解:(1)∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°,
∴∠AOC=70°,∠AOD=110°,
∵∠BOD=∠AOC,
∴∠BOD=70°,
∵OE平分∠BOD,
∴∠DOE=35°,
∴∠COE=180°﹣∠DOE=145°;
(2)分两种情况,
如图1,∵OF⊥OE,
∴∠EOF=90°,
∴∠COF=∠COE﹣∠EOF=145°﹣90°=55°,
如图2,∠COF=∠360°﹣∠COE﹣∠EOF=125°.
19.(8分)如图,在三角形△ABC中,∠BCA=90°,BC=3,AC=4,AB=5.点P是线段AB上的一动点,求线段CP的最小值是多少?
解:当CP垂直AB时有最小值,
因为:∠BCA=90°,BC=3,AC=4,AB=5,
∴S△ABC=BC?AC=AB?CP,
即×3×4=×5CP,
解得CP=2.4,
答:CP的最小值是2.4.
20.(8分)如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?
解:点B在点A北偏东35°方向,点C在点B北偏西55°方向,
∴∠CBA=90°,
点C到直线AB的距离是BC的长,
∵BC=10m,
∴点C到直线AB的距离是10m.
21.(10分)说出下列各对角分别是哪一条直线截哪两条直线形成什么角?
(1)∠A和∠ACG
(2)∠ACF和∠CED
(3)∠AED和∠ACB
(4)∠B和∠BCG.
解:(1)∠A和∠ACG是直线AC截直线CG、AB形成的内错角;
(2)∠ACF和∠CED是直线AC截直线FB、ED形成的内错角;
(3)∠AED和∠ACB是直线AC截直线DE、FB形成的同位角;
(4)∠B和∠BCG是直线FB截直线CG、AB形成的同旁内角;
22.(10分)已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
(1)解:∵当AC⊥直线a时,A为垂足,此时d=AC=2厘米,
∴0<d≤2;
(2)解:如图所示:
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
