第二章平行线与相交线全章复习 基础检测
文档属性
| 名称 | 第二章平行线与相交线全章复习 基础检测 |

|
|
| 格式 | zip | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-24 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
1)两个角的和是直角,称这两个角互为 .
2)两个角的和是平角,称这两个角互为 .
3)有公共顶点,两边互为反向延长线的两个角叫做 .
4)同角或等角的余角______;
5)同角或_____的补角相等;
6)对顶角______。
7)平行线的判定方法:
①同位角相等,两直线 ;
②内错角相等,两直线 ;
③同旁内角 ,两直线平行.
8)平行线的特征:
①两直线 ,同位角相等;
②两直线平行,内错角 ;
③两直线平行, 互补;
9)当两条直线相交所成的四个角中有一个角是直角时,就说这两条直线 ,它们的交点叫做 .
10)直线外一点到直线上各点连结的所有线段中,垂线段 ,这条垂线段的长度叫做 .
11)经过直线外一点,有且只有 条直线与这条直线平行;过一点有且只有 _____条直线与已知直线垂直.
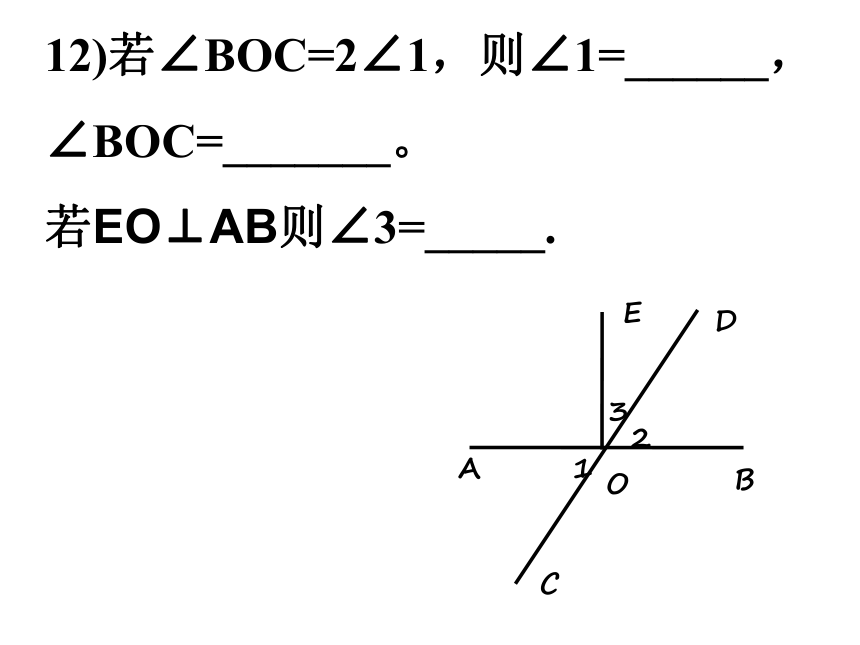
12)若∠BOC=2∠1,则∠1=______,
∠BOC=_______。
若EO⊥AB则∠3=_____.
E
3
A
B
C
D
O
2
1
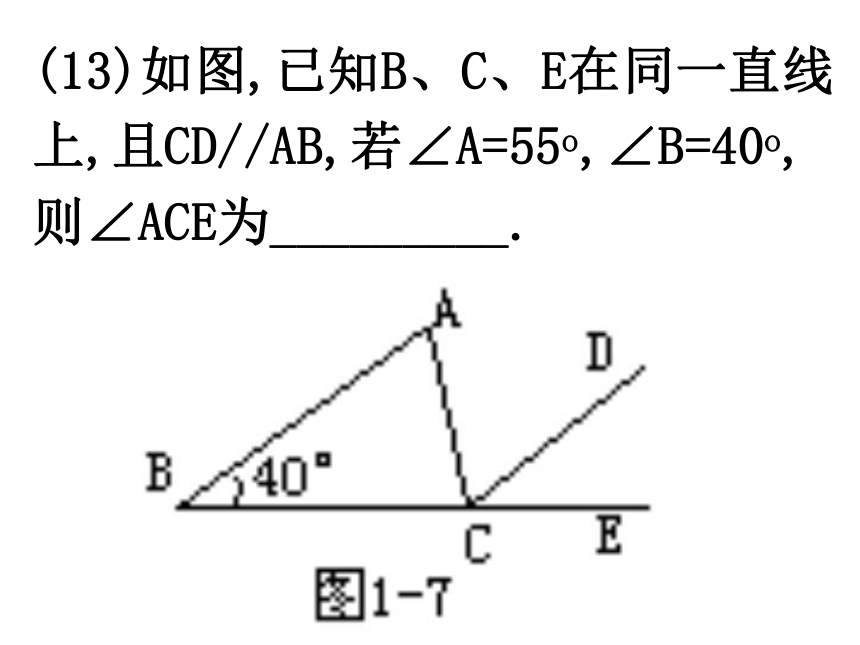
(13)如图,已知B、C、E在同一直线上,且CD//AB,若∠A=55o,∠B=40o,
则∠ACE为_________.
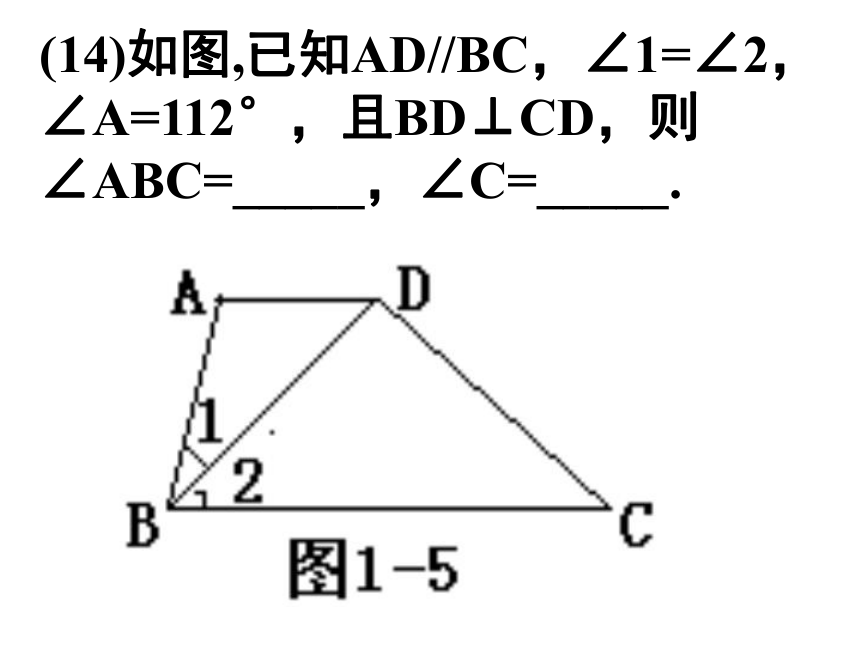
(14)如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.
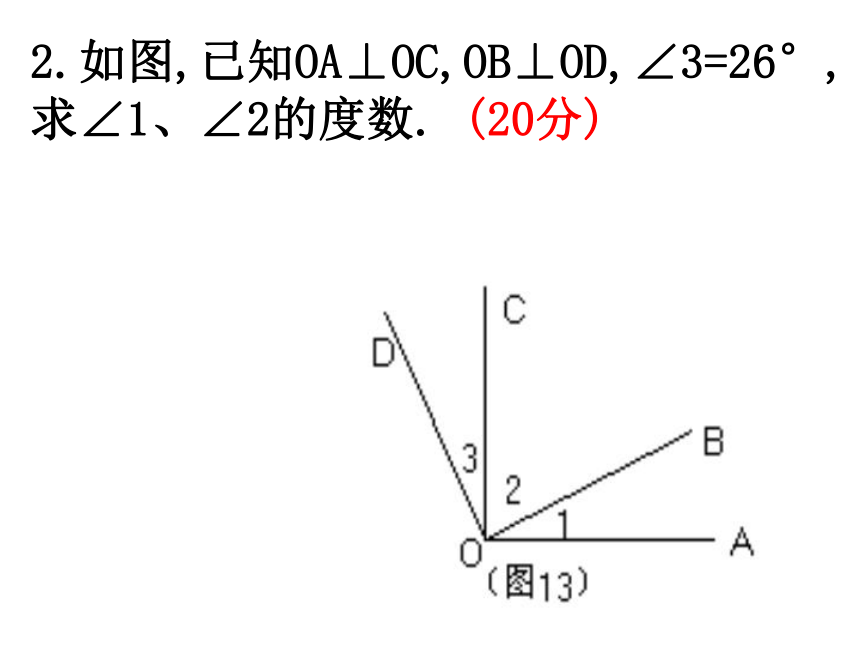
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数. (20分)
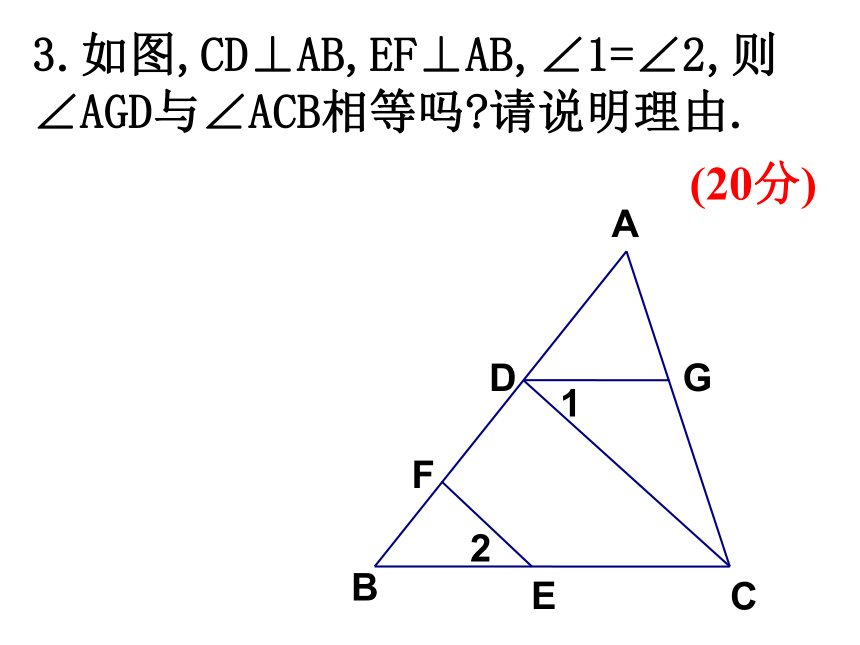
3.如图,CD⊥AB,EF⊥AB,∠1=∠2,则∠AGD与∠ACB相等吗 请说明理由.
2
1
E
F
D
G
C
B
A
(20分)
1)两个角的和是直角,称这两个角互为 .
2)两个角的和是平角,称这两个角互为 .
3)有公共顶点,两边互为反向延长线的两个角叫做 .
4)同角或等角的余角______;
5)同角或_____的补角相等;
6)对顶角______。
补角
余角
对顶角
相等
等角
相等
7)平行线的判定方法:
①同位角相等,两直线 ;
②内错角相等,两直线 ;
③同旁内角 ,两直线平行.
8)平行线的特征:
①两直线 ,同位角相等;
②两直线平行,内错角 ;
③两直线平行, 互补;
平行
平行
互补
平行
相等
同旁内角
9)当两条直线相交所成的四个角中有一个角是直角时,就说这两条直线________,它们的交点叫做 .
10)直线外一点到直线上各点连结的所有线段中,垂线段 ,这条垂线段的长度叫做 .
11)经过直线外一点,有且只有 条直线与这条直线平行;过一点有且只有 _____条直线与已知直线垂直.
互相垂直
垂足
最短
点到直线的距离
一
一
12)若∠BOC=2∠1,则∠1=______,
∠BOC=_______。
若EO⊥AB,则∠3=_____.
E
3
A
B
C
D
O
2
1
60o
120o
30o
(13)如图,已知B、C、E在同一直线上,且CD//AB,若∠A=55o,∠B=40o,
则∠ACE为_________.
95O
(14)如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.
68o
56o
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数. (20分)
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数.
解:∵ OB⊥OD (已知),
∴ ∠BOD=90°(垂直定义).
即 ∠2+ ∠3= 90°.
又∵∠3=26°(已知),
∴ ∠2 + 26°= 90°(等量代换).
∴ ∠2=64° (等式的性质).
又∵ OA⊥OC (已知),
∴ ∠1+ ∠2= 90°(垂直定义).
∴ ∠1= ∠3=26o(同角的余角相等).
3.如图,CD⊥AB,EF⊥AB,∠1=∠2,则∠AGD与∠ACB相等吗 请说明理由.
2
1
E
F
D
G
C
B
A
(20分)
∠AGD= ∠ACB.
理由:
∵CD⊥AB,EF⊥AB
∴CD∥EF
∴∠2=∠DCB
又∵∠1=∠2
∴∠DCB =∠1
∴DG∥BC
∴∠AGD=∠ACB
甲
乙
北
北
42 °
南偏西42 °度
★ ★ ★如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42o.甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度 为什么
1)两个角的和是直角,称这两个角互为 .
2)两个角的和是平角,称这两个角互为 .
3)有公共顶点,两边互为反向延长线的两个角叫做 .
4)同角或等角的余角______;
5)同角或_____的补角相等;
6)对顶角______。
7)平行线的判定方法:
①同位角相等,两直线 ;
②内错角相等,两直线 ;
③同旁内角 ,两直线平行.
8)平行线的特征:
①两直线 ,同位角相等;
②两直线平行,内错角 ;
③两直线平行, 互补;
9)当两条直线相交所成的四个角中有一个角是直角时,就说这两条直线 ,它们的交点叫做 .
10)直线外一点到直线上各点连结的所有线段中,垂线段 ,这条垂线段的长度叫做 .
11)经过直线外一点,有且只有 条直线与这条直线平行;过一点有且只有 _____条直线与已知直线垂直.
12)若∠BOC=2∠1,则∠1=______,
∠BOC=_______。
若EO⊥AB则∠3=_____.
E
3
A
B
C
D
O
2
1
(13)如图,已知B、C、E在同一直线上,且CD//AB,若∠A=55o,∠B=40o,
则∠ACE为_________.
(14)如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数. (20分)
3.如图,CD⊥AB,EF⊥AB,∠1=∠2,则∠AGD与∠ACB相等吗 请说明理由.
2
1
E
F
D
G
C
B
A
(20分)
1)两个角的和是直角,称这两个角互为 .
2)两个角的和是平角,称这两个角互为 .
3)有公共顶点,两边互为反向延长线的两个角叫做 .
4)同角或等角的余角______;
5)同角或_____的补角相等;
6)对顶角______。
补角
余角
对顶角
相等
等角
相等
7)平行线的判定方法:
①同位角相等,两直线 ;
②内错角相等,两直线 ;
③同旁内角 ,两直线平行.
8)平行线的特征:
①两直线 ,同位角相等;
②两直线平行,内错角 ;
③两直线平行, 互补;
平行
平行
互补
平行
相等
同旁内角
9)当两条直线相交所成的四个角中有一个角是直角时,就说这两条直线________,它们的交点叫做 .
10)直线外一点到直线上各点连结的所有线段中,垂线段 ,这条垂线段的长度叫做 .
11)经过直线外一点,有且只有 条直线与这条直线平行;过一点有且只有 _____条直线与已知直线垂直.
互相垂直
垂足
最短
点到直线的距离
一
一
12)若∠BOC=2∠1,则∠1=______,
∠BOC=_______。
若EO⊥AB,则∠3=_____.
E
3
A
B
C
D
O
2
1
60o
120o
30o
(13)如图,已知B、C、E在同一直线上,且CD//AB,若∠A=55o,∠B=40o,
则∠ACE为_________.
95O
(14)如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.
68o
56o
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数. (20分)
2.如图,已知OA⊥OC,OB⊥OD,∠3=26°,求∠1、∠2的度数.
解:∵ OB⊥OD (已知),
∴ ∠BOD=90°(垂直定义).
即 ∠2+ ∠3= 90°.
又∵∠3=26°(已知),
∴ ∠2 + 26°= 90°(等量代换).
∴ ∠2=64° (等式的性质).
又∵ OA⊥OC (已知),
∴ ∠1+ ∠2= 90°(垂直定义).
∴ ∠1= ∠3=26o(同角的余角相等).
3.如图,CD⊥AB,EF⊥AB,∠1=∠2,则∠AGD与∠ACB相等吗 请说明理由.
2
1
E
F
D
G
C
B
A
(20分)
∠AGD= ∠ACB.
理由:
∵CD⊥AB,EF⊥AB
∴CD∥EF
∴∠2=∠DCB
又∵∠1=∠2
∴∠DCB =∠1
∴DG∥BC
∴∠AGD=∠ACB
甲
乙
北
北
42 °
南偏西42 °度
★ ★ ★如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42o.甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度 为什么
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
