2020-2021学年人教版初中数学八年级下册 19.2 一次函数的图像和性质同步测试(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版初中数学八年级下册 19.2 一次函数的图像和性质同步测试(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览




文档简介
人教版初中数学八年级下册
19.2
一次函数的图像和性质同步测试(解析版)
一.选择题
1.已知函数y=kx﹣1,且y随x的增大而减小,则它的图象是( )
A.
B.
C.
D.
2.对于函数y=﹣2x+1,下列结论正确的是( )
A.它的图象必经过点(﹣1,3)
B.它的图象经过第一、二、三象限
C.当时,y>0
D.y值随x值的增大而增大
3.一次函数y=(m﹣1)x+m2的图象过点(0,4),且过一、二、三象限,则m=( )
A.﹣2
B.2
C.2或3
D.﹣2或2
4.若点(a,b)在一次函数y=2x﹣3的图象上,则代数式4b﹣8a+2的值是( )
A.﹣10
B.﹣6
C.10
D.14
5.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2
B.﹣2
C.3
D.﹣3
6.在直线y=x+上且到x轴或y轴距离为1的点有( )个.
A.1
B.2
C.3
D.4
7.直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20
B.10
C.40
D.12
8.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.m>1
B.m<﹣5
C.﹣5<m<1
D.m<1
9.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是( )
A.﹣1≤b≤1
B.﹣≤b≤1
C.﹣≤b≤
D.﹣1≤b≤
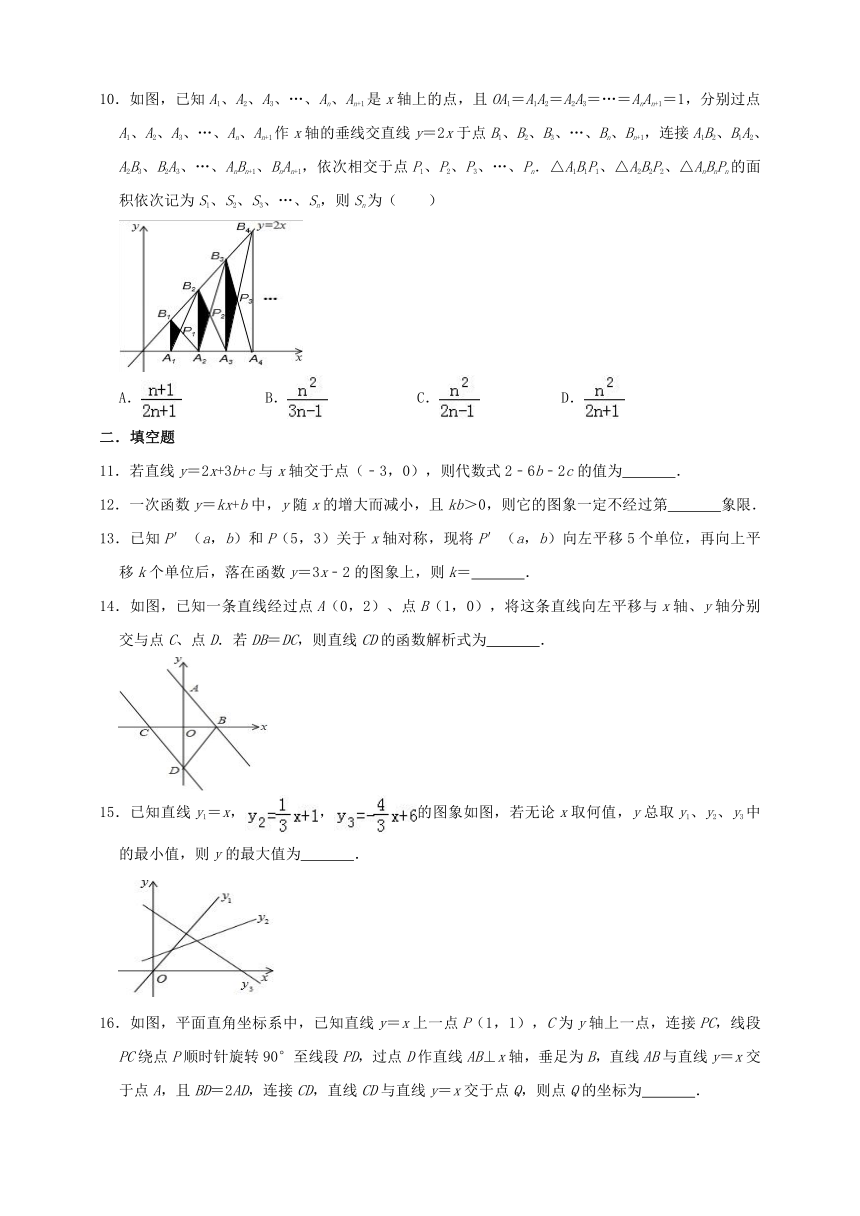
10.如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A.
B.
C.
D.
二.填空题
11.若直线y=2x+3b+c与x轴交于点(﹣3,0),则代数式2﹣6b﹣2c的值为
.
12.一次函数y=kx+b中,y随x的增大而减小,且kb>0,则它的图象一定不经过第
象限.
13.已知P′(a,b)和P(5,3)关于x轴对称,现将P′(a,b)向左平移5个单位,再向上平移k个单位后,落在函数y=3x﹣2的图象上,则k=
.
14.如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为
.
15.已知直线y1=x,,的图象如图,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为
.
16.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为
.
三.解答题
17.如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的解析式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
18.一次函数y=ax﹣a+1(a为常数,且a≠0).
(1)若点在一次函数y=ax﹣a+1的图象上,求a的值;
(2)当﹣1≤x≤2时,函数有最大值2,请求出a的值.
19.已知一次函数图象经过点(3,5),(﹣4,﹣9)两点.
(1)求一次函数解析式.
(2)求图象和坐标轴交点坐标.
(3)求图象和坐标轴围成三角形面积.
(4)点(a,2)在图象上,求a的值.
20.如图,直线l1的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x、y的二元一次方程组的解.
21.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
(1)求函数y=﹣x+3的坐标三角形的三条边长;
(2)若函数y=kx﹣3(k为常数)的坐标三角形面积为6,求该函数的表达式;
(3)若函数y=﹣x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
22.已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=
;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=﹣x+b,求n的值.
23.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
(1)求AB、BD的长度,并证明△ABD是直角三角形;
(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;
(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.
参考答案与试题解析
一.选择题
1.已知函数y=kx﹣1,且y随x的增大而减小,则它的图象是( )
A.B.
C.
D.
解:∵一次函数y=kx﹣1,且y随着x的增大而减小
∴k<0,
又∵b=﹣1<0
∴此一次函数图形过第二,三,四象限.
故选:B.
2.对于函数y=﹣2x+1,下列结论正确的是( )
A.它的图象必经过点(﹣1,3)
B.它的图象经过第一、二、三象限
C.当时,y>0
D.y值随x值的增大而增大
解:当x=﹣1时,y=3,故A选项正确,
∵函数y=2x+1图象经过第一、二、四象限,y随x的增大而减小,
∴B、D选项错误,
∵y>0,∴﹣2x+1>0∴x<∴C选项错误,故选:A.
3.一次函数y=(m﹣1)x+m2的图象过点(0,4),且过一、二、三象限,则m=( )
A.﹣2
B.2
C.2或3
D.﹣2或2
解:∵一次函数y=(m﹣1)x+m2的图象过点(0,4),
∴m2=4,解得:m=±2,∵过一、二、三象限,∴m﹣1>0,
解得:m>1,故m的值为2,故选:B.
4.若点(a,b)在一次函数y=2x﹣3的图象上,则代数式4b﹣8a+2的值是( )
A.﹣10
B.﹣6
C.10
D.14
解:∵点P(a,b)在一次函数y=2x﹣3的图象上,
∴2a﹣3=b,即2a﹣b=3,
∴4b﹣8a+2=﹣4(2a﹣b)+2=﹣4×3+2=﹣10.
故选:A.
5.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2
B.﹣2
C.3
D.﹣3
解:∵y与(x﹣2)成正比例,∴设y=k(x﹣2),
由题意得,﹣2=k(1﹣2),解得,k=2,则y=2x﹣4,
当x=3时,y=2×3﹣4=2,故选:A.
6.在直线y=x+上且到x轴或y轴距离为1的点有( )个.
A.1
B.2
C.3
D.4
解:根据题意,得:把x=±1分别代入,得:y=1或0,
把y=±1分别代入,得x=1或﹣3,
故满足条件的点有(1,1)或(﹣1,0)或(﹣3,﹣1),共3个.
故选:C.
7.直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20
B.10
C.40
D.12
解:∵直线y=﹣x+6与y轴的交点为(0,6),直线y=x﹣2与y轴的交点分别为(0,﹣2),
∴两条直线与y轴交点之间距离为|6+2|=8,由题意得,
解得,故两直线的交点坐标为(5,3),
∴两直线与y轴围成的三角形的面积=×8×5=20.故选:A.
8.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.m>1
B.m<﹣5
C.﹣5<m<1
D.m<1
解:直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,
联立两直线解析式得:,解得:,
即交点坐标为(,),
∵交点在第二象限,∴,解得:﹣5<m<1.故选:C.
9.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是( )
A.﹣1≤b≤1
B.﹣≤b≤1
C.﹣≤b≤
D.﹣1≤b≤
解:直线y=x+b经过点B时,将B(3,1)代入直线中,可得+b=1,解得b=﹣;
直线y=x+b经过点A时:将A(1,1)代入直线中,可得+b=1,解得b=;
直线y=x+b经过点C时:将C(2,2)代入直线中,可得1+b=2,解得b=1.
故b的取值范围是﹣≤b≤1.
故选:B.
10.如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A.
B.
C.
D.
解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,2),B2(2,4),B3(3,6),…,Bn(n,2n)
∵A1B1∥A2B2,∴△A1B1P1∽△A2B2P1,∴=,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,∵A1A2=1,∴A1B1边上的高为:,
∴=××2=,
同理可得:=,=,∴Sn=.
故选:D.
二.填空题
11.若直线y=2x+3b+c与x轴交于点(﹣3,0),则代数式2﹣6b﹣2c的值为 ﹣10 .
解:∵直线y=2x+3b+c与x轴交于点(﹣3,0),
∴0=2×(﹣3)+3b+c,
∴3b+c=6,
∴2﹣6b﹣2c=2﹣2(3b+c)=2﹣2×6=﹣10.
故答案为﹣10.
12.一次函数y=kx+b中,y随x的增大而减小,且kb>0,则它的图象一定不经过第 一 象限.
解:∵一次函数y=kx+b中,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0.
根据一次函数的图象即可得出:该一次函数一定不经过第一象限.
故答案为:一.
13.已知P′(a,b)和P(5,3)关于x轴对称,现将P′(a,b)向左平移5个单位,再向上平移k个单位后,落在函数y=3x﹣2的图象上,则k= 1 .
解:∵P′(a,b)和P(5,3)关于x轴对称,
∴a=5,b=﹣3,∴P′(5,﹣3),
∴将P′(5,﹣3)向左平移5个单位后的坐标为(0,﹣3),再向上平移k个单位后的坐标为(0,﹣3+k),
∵平移后的点的坐标落在函数y=3x﹣2的图象上,
∴﹣3+k=﹣2,解得,k=1.故答案为1.
14.如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 y=﹣2x﹣2 .
解:设直线AB的解析式为y=kx+b,
把A(0,2)、点B(1,0)代入,得,解得,
故直线AB的解析式为y=﹣2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC,
∴DO垂直平分BC,∴OC=OB,
∵直线CD由直线AB平移而成,∴CD=AB,∴点D的坐标为(0,﹣2),
∵平移后的图形与原图形平行,∴平移以后的函数解析式为:y=﹣2x﹣2.
故答案为:y=﹣2x﹣2.
15.已知直线y1=x,,的图象如图,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为 2 .
解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,
联立,解得,所以,当x=3时,y的值最大,为2.故答案为:2.
16.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为 (,) .
解:过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
∠CMP=∠DNP=∠CPD=90°,∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,∵P(1,1),∴OM=BN=1,PM=1,
在△MCP和△NPD中∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,∵BD=2AD,∴设AD=a,BD=2a,
∵P(1,1),∴DN=2a﹣1,则2a﹣1=1,a=1,即BD=2.
∵直线y=x,∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD==,
在Rt△MCP中,由勾股定理得:CM==2,
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,把D(3,2)代入得:k=﹣,
即直线CD的解析式是y=﹣x+3,
即方程组得:,即Q的坐标是(,),
②当点C在y轴的负半轴上时,作PN⊥AD于N,交y轴于H,此时不满足BD=2AD,
故答案为:(,).
三.解答题
17.如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的解析式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
解:(1)设直线l1的解析式为y=kx+b(k≠0),
∵一次函数的图象经过点A(﹣1,0)和点B(1,4).∴,解得,
∴直线l1的解析式为y=2x+2;
(2)∵△APB的面积为8,点B(1,4),∴×AP×4=8,解得:AP=4,
∵点A(﹣1,0),∴P(﹣5,0)或(3,0).
18.一次函数y=ax﹣a+1(a为常数,且a≠0).
(1)若点在一次函数y=ax﹣a+1的图象上,求a的值;
(2)当﹣1≤x≤2时,函数有最大值2,请求出a的值.
解:(1)把(﹣,3)代入y=ax﹣a+1得﹣a﹣a+1=3,解得a=;
(2)①a>0时,y随x的增大而增大,
则当x=2时,y有最大值2,把x=2,y=2代入函数关系式得2=2a﹣a+1,解得a=1;
②a<0时,y随x的增大而减小,
则当x=﹣1时,y有最大值2,把x=﹣1代入函数关系式得
2=﹣a﹣a+1,解得a=﹣,
所以或a=1.
19.已知一次函数图象经过点(3,5),(﹣4,﹣9)两点.
(1)求一次函数解析式.
(2)求图象和坐标轴交点坐标.
(3)求图象和坐标轴围成三角形面积.
(4)点(a,2)在图象上,求a的值.
解:(1)设一次函数解析式为y=kx+b,
把点(3,5),(﹣4,﹣9)分别代入解析式得,则,解得,
∴一次函数解析式为y=2x﹣1;
(2)当x=0时,y=﹣1,当y=0时,2x﹣1=0,解得:x=,
∴与坐标轴的交点为(0,﹣1)、(,0);
(3)S△=××|﹣1|=;
(4)∵点(a,2)在图象上,∴2a﹣1=2,∴a=.
20.如图,直线l1的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x、y的二元一次方程组的解.
解:(1)∵点D是直线l1:y=2x﹣2与x轴的交点,
∴y=0,0=2x﹣2,x=1,∴D(1,0),
∵点C在直线l1:y=2x﹣2上,∴2=2m﹣2,m=2,∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,
∴,解之得:,∴直线l2的解析式为y=﹣x+4;
(3)∵点A是直线l2与x轴的交点,
∴y=0,即0=﹣x+4,解得x=4,即点A(4,0),
所以,AD=4﹣1=3,S△ADC=×3×2=3;
(4)由图可知的解为.
21.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
(1)求函数y=﹣x+3的坐标三角形的三条边长;
(2)若函数y=kx﹣3(k为常数)的坐标三角形面积为6,求该函数的表达式;
(3)若函数y=﹣x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
解:(1)∵直线y=﹣x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=﹣x+3的坐标三角形的三条边长分别为3,4,5;
(2)∵函数y=kx﹣3与x轴的交点坐标为(,0),与y轴交点坐标为(0,﹣3),
∴OA=||,OB=|﹣3|=3,
∵S△AOB=6,∴×||×3=6,∴||=4,∴k=±,
∴当函数y=kx﹣3(k为常数)的坐标三角形面积为6时,该函数的表达式为y=x﹣3或y=﹣x﹣3;
(3)直线y=﹣x+b与x轴的交点坐标为(b,0),与y轴交点坐标为(0,b),
AB===b,
当b>0时,b+b+b=16,得b=4,
此时,S△AOB=OA?OB=××4=,
即坐标三角形面积为;
当b<0时,﹣b﹣b﹣b=16,得b=﹣4,
此时,S△AOB=OA?OB=××4=,
即坐标三角形面积为.
综上,当函数y=﹣x+b的坐标三角形周长为16时,面积为.
22.已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= 2 ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=﹣x+b,求n的值.
解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x﹣2+b,
由题意,得0=0﹣2+b,解得b=2.故答案为2;
(2)∵当x=0时,y=4,∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,∴(0,4)在函数y=x+b图象上.∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(﹣4,0).
∵y2=kx﹣4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx﹣4的图象经过点(4,0),则0=4k+4,∴k=﹣1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=﹣b,
∴y1=x+b图象与x轴交于点A(﹣b,0).
如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=,
∴y3=﹣x+b图象与x轴交于点C(,0).
如图,∵CO=,∴tan∠ACB==,∴∠ACB=60°.
∴n°=180°﹣∠ACB﹣∠BAC=75°.即n的值为75.
23.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
(1)求AB、BD的长度,并证明△ABD是直角三角形;
(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;
(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.
解:(1)令x=0,y=4,令y=0,则﹣x+4=0,
解得x=3,所以,A(0,4),B(3,0),
由勾股定理得,AB==5,BD==10,
过点D作DH⊥y轴于H,DH=11,AH=2,
由勾股定理得,AD===,
∵AB2=25,BD2=100,∴AB2+BD2=AD2,
∴△ABD是直角三角形;
(2)设OC长为x,由等腰三角形以及勾股定理得到x2+42=(11﹣x)2+62,
解得x=,所以,C(,0);
(3)设t秒时相遇,由题意得,t+t=5+10,解得t=7.5,
点P在AB上时,0≤t≤5,PB=5﹣t,BQ=10﹣t,
PQ===,
所以,y=,
点P、Q都在BD上重合前,5<t≤7.5,PQ=5+10﹣t﹣t=15﹣2t,
重合后,7.5<t≤10,PQ=t+t﹣5﹣10=2t﹣15,
所以,y=2t﹣15,
点Q在AB上时,10<t≤15,PB=t﹣5,BQ=t﹣10,
PQ===,
所以,y=.
19.2
一次函数的图像和性质同步测试(解析版)
一.选择题
1.已知函数y=kx﹣1,且y随x的增大而减小,则它的图象是( )
A.
B.
C.
D.
2.对于函数y=﹣2x+1,下列结论正确的是( )
A.它的图象必经过点(﹣1,3)
B.它的图象经过第一、二、三象限
C.当时,y>0
D.y值随x值的增大而增大
3.一次函数y=(m﹣1)x+m2的图象过点(0,4),且过一、二、三象限,则m=( )
A.﹣2
B.2
C.2或3
D.﹣2或2
4.若点(a,b)在一次函数y=2x﹣3的图象上,则代数式4b﹣8a+2的值是( )
A.﹣10
B.﹣6
C.10
D.14
5.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2
B.﹣2
C.3
D.﹣3
6.在直线y=x+上且到x轴或y轴距离为1的点有( )个.
A.1
B.2
C.3
D.4
7.直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20
B.10
C.40
D.12
8.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.m>1
B.m<﹣5
C.﹣5<m<1
D.m<1
9.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是( )
A.﹣1≤b≤1
B.﹣≤b≤1
C.﹣≤b≤
D.﹣1≤b≤
10.如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A.
B.
C.
D.
二.填空题
11.若直线y=2x+3b+c与x轴交于点(﹣3,0),则代数式2﹣6b﹣2c的值为
.
12.一次函数y=kx+b中,y随x的增大而减小,且kb>0,则它的图象一定不经过第
象限.
13.已知P′(a,b)和P(5,3)关于x轴对称,现将P′(a,b)向左平移5个单位,再向上平移k个单位后,落在函数y=3x﹣2的图象上,则k=
.
14.如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为
.
15.已知直线y1=x,,的图象如图,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为
.
16.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为
.
三.解答题
17.如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的解析式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
18.一次函数y=ax﹣a+1(a为常数,且a≠0).
(1)若点在一次函数y=ax﹣a+1的图象上,求a的值;
(2)当﹣1≤x≤2时,函数有最大值2,请求出a的值.
19.已知一次函数图象经过点(3,5),(﹣4,﹣9)两点.
(1)求一次函数解析式.
(2)求图象和坐标轴交点坐标.
(3)求图象和坐标轴围成三角形面积.
(4)点(a,2)在图象上,求a的值.
20.如图,直线l1的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x、y的二元一次方程组的解.
21.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
(1)求函数y=﹣x+3的坐标三角形的三条边长;
(2)若函数y=kx﹣3(k为常数)的坐标三角形面积为6,求该函数的表达式;
(3)若函数y=﹣x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
22.已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=
;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=﹣x+b,求n的值.
23.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
(1)求AB、BD的长度,并证明△ABD是直角三角形;
(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;
(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.
参考答案与试题解析
一.选择题
1.已知函数y=kx﹣1,且y随x的增大而减小,则它的图象是( )
A.B.
C.
D.
解:∵一次函数y=kx﹣1,且y随着x的增大而减小
∴k<0,
又∵b=﹣1<0
∴此一次函数图形过第二,三,四象限.
故选:B.
2.对于函数y=﹣2x+1,下列结论正确的是( )
A.它的图象必经过点(﹣1,3)
B.它的图象经过第一、二、三象限
C.当时,y>0
D.y值随x值的增大而增大
解:当x=﹣1时,y=3,故A选项正确,
∵函数y=2x+1图象经过第一、二、四象限,y随x的增大而减小,
∴B、D选项错误,
∵y>0,∴﹣2x+1>0∴x<∴C选项错误,故选:A.
3.一次函数y=(m﹣1)x+m2的图象过点(0,4),且过一、二、三象限,则m=( )
A.﹣2
B.2
C.2或3
D.﹣2或2
解:∵一次函数y=(m﹣1)x+m2的图象过点(0,4),
∴m2=4,解得:m=±2,∵过一、二、三象限,∴m﹣1>0,
解得:m>1,故m的值为2,故选:B.
4.若点(a,b)在一次函数y=2x﹣3的图象上,则代数式4b﹣8a+2的值是( )
A.﹣10
B.﹣6
C.10
D.14
解:∵点P(a,b)在一次函数y=2x﹣3的图象上,
∴2a﹣3=b,即2a﹣b=3,
∴4b﹣8a+2=﹣4(2a﹣b)+2=﹣4×3+2=﹣10.
故选:A.
5.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2
B.﹣2
C.3
D.﹣3
解:∵y与(x﹣2)成正比例,∴设y=k(x﹣2),
由题意得,﹣2=k(1﹣2),解得,k=2,则y=2x﹣4,
当x=3时,y=2×3﹣4=2,故选:A.
6.在直线y=x+上且到x轴或y轴距离为1的点有( )个.
A.1
B.2
C.3
D.4
解:根据题意,得:把x=±1分别代入,得:y=1或0,
把y=±1分别代入,得x=1或﹣3,
故满足条件的点有(1,1)或(﹣1,0)或(﹣3,﹣1),共3个.
故选:C.
7.直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20
B.10
C.40
D.12
解:∵直线y=﹣x+6与y轴的交点为(0,6),直线y=x﹣2与y轴的交点分别为(0,﹣2),
∴两条直线与y轴交点之间距离为|6+2|=8,由题意得,
解得,故两直线的交点坐标为(5,3),
∴两直线与y轴围成的三角形的面积=×8×5=20.故选:A.
8.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.m>1
B.m<﹣5
C.﹣5<m<1
D.m<1
解:直线y=﹣x+3向上平移m个单位后可得:y=﹣x+3+m,
联立两直线解析式得:,解得:,
即交点坐标为(,),
∵交点在第二象限,∴,解得:﹣5<m<1.故选:C.
9.如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线与△ABC有交点时,b的取值范围是( )
A.﹣1≤b≤1
B.﹣≤b≤1
C.﹣≤b≤
D.﹣1≤b≤
解:直线y=x+b经过点B时,将B(3,1)代入直线中,可得+b=1,解得b=﹣;
直线y=x+b经过点A时:将A(1,1)代入直线中,可得+b=1,解得b=;
直线y=x+b经过点C时:将C(2,2)代入直线中,可得1+b=2,解得b=1.
故b的取值范围是﹣≤b≤1.
故选:B.
10.如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A.
B.
C.
D.
解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,2),B2(2,4),B3(3,6),…,Bn(n,2n)
∵A1B1∥A2B2,∴△A1B1P1∽△A2B2P1,∴=,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,∵A1A2=1,∴A1B1边上的高为:,
∴=××2=,
同理可得:=,=,∴Sn=.
故选:D.
二.填空题
11.若直线y=2x+3b+c与x轴交于点(﹣3,0),则代数式2﹣6b﹣2c的值为 ﹣10 .
解:∵直线y=2x+3b+c与x轴交于点(﹣3,0),
∴0=2×(﹣3)+3b+c,
∴3b+c=6,
∴2﹣6b﹣2c=2﹣2(3b+c)=2﹣2×6=﹣10.
故答案为﹣10.
12.一次函数y=kx+b中,y随x的增大而减小,且kb>0,则它的图象一定不经过第 一 象限.
解:∵一次函数y=kx+b中,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0.
根据一次函数的图象即可得出:该一次函数一定不经过第一象限.
故答案为:一.
13.已知P′(a,b)和P(5,3)关于x轴对称,现将P′(a,b)向左平移5个单位,再向上平移k个单位后,落在函数y=3x﹣2的图象上,则k= 1 .
解:∵P′(a,b)和P(5,3)关于x轴对称,
∴a=5,b=﹣3,∴P′(5,﹣3),
∴将P′(5,﹣3)向左平移5个单位后的坐标为(0,﹣3),再向上平移k个单位后的坐标为(0,﹣3+k),
∵平移后的点的坐标落在函数y=3x﹣2的图象上,
∴﹣3+k=﹣2,解得,k=1.故答案为1.
14.如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 y=﹣2x﹣2 .
解:设直线AB的解析式为y=kx+b,
把A(0,2)、点B(1,0)代入,得,解得,
故直线AB的解析式为y=﹣2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC,
∴DO垂直平分BC,∴OC=OB,
∵直线CD由直线AB平移而成,∴CD=AB,∴点D的坐标为(0,﹣2),
∵平移后的图形与原图形平行,∴平移以后的函数解析式为:y=﹣2x﹣2.
故答案为:y=﹣2x﹣2.
15.已知直线y1=x,,的图象如图,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为 2 .
解:根据题意,y的最大值为直线y2与y3的交点的纵坐标,
联立,解得,所以,当x=3时,y的值最大,为2.故答案为:2.
16.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为 (,) .
解:过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
∠CMP=∠DNP=∠CPD=90°,∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,∵P(1,1),∴OM=BN=1,PM=1,
在△MCP和△NPD中∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,∵BD=2AD,∴设AD=a,BD=2a,
∵P(1,1),∴DN=2a﹣1,则2a﹣1=1,a=1,即BD=2.
∵直线y=x,∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD==,
在Rt△MCP中,由勾股定理得:CM==2,
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,把D(3,2)代入得:k=﹣,
即直线CD的解析式是y=﹣x+3,
即方程组得:,即Q的坐标是(,),
②当点C在y轴的负半轴上时,作PN⊥AD于N,交y轴于H,此时不满足BD=2AD,
故答案为:(,).
三.解答题
17.如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的解析式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
解:(1)设直线l1的解析式为y=kx+b(k≠0),
∵一次函数的图象经过点A(﹣1,0)和点B(1,4).∴,解得,
∴直线l1的解析式为y=2x+2;
(2)∵△APB的面积为8,点B(1,4),∴×AP×4=8,解得:AP=4,
∵点A(﹣1,0),∴P(﹣5,0)或(3,0).
18.一次函数y=ax﹣a+1(a为常数,且a≠0).
(1)若点在一次函数y=ax﹣a+1的图象上,求a的值;
(2)当﹣1≤x≤2时,函数有最大值2,请求出a的值.
解:(1)把(﹣,3)代入y=ax﹣a+1得﹣a﹣a+1=3,解得a=;
(2)①a>0时,y随x的增大而增大,
则当x=2时,y有最大值2,把x=2,y=2代入函数关系式得2=2a﹣a+1,解得a=1;
②a<0时,y随x的增大而减小,
则当x=﹣1时,y有最大值2,把x=﹣1代入函数关系式得
2=﹣a﹣a+1,解得a=﹣,
所以或a=1.
19.已知一次函数图象经过点(3,5),(﹣4,﹣9)两点.
(1)求一次函数解析式.
(2)求图象和坐标轴交点坐标.
(3)求图象和坐标轴围成三角形面积.
(4)点(a,2)在图象上,求a的值.
解:(1)设一次函数解析式为y=kx+b,
把点(3,5),(﹣4,﹣9)分别代入解析式得,则,解得,
∴一次函数解析式为y=2x﹣1;
(2)当x=0时,y=﹣1,当y=0时,2x﹣1=0,解得:x=,
∴与坐标轴的交点为(0,﹣1)、(,0);
(3)S△=××|﹣1|=;
(4)∵点(a,2)在图象上,∴2a﹣1=2,∴a=.
20.如图,直线l1的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x、y的二元一次方程组的解.
解:(1)∵点D是直线l1:y=2x﹣2与x轴的交点,
∴y=0,0=2x﹣2,x=1,∴D(1,0),
∵点C在直线l1:y=2x﹣2上,∴2=2m﹣2,m=2,∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,
∴,解之得:,∴直线l2的解析式为y=﹣x+4;
(3)∵点A是直线l2与x轴的交点,
∴y=0,即0=﹣x+4,解得x=4,即点A(4,0),
所以,AD=4﹣1=3,S△ADC=×3×2=3;
(4)由图可知的解为.
21.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
(1)求函数y=﹣x+3的坐标三角形的三条边长;
(2)若函数y=kx﹣3(k为常数)的坐标三角形面积为6,求该函数的表达式;
(3)若函数y=﹣x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
解:(1)∵直线y=﹣x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=﹣x+3的坐标三角形的三条边长分别为3,4,5;
(2)∵函数y=kx﹣3与x轴的交点坐标为(,0),与y轴交点坐标为(0,﹣3),
∴OA=||,OB=|﹣3|=3,
∵S△AOB=6,∴×||×3=6,∴||=4,∴k=±,
∴当函数y=kx﹣3(k为常数)的坐标三角形面积为6时,该函数的表达式为y=x﹣3或y=﹣x﹣3;
(3)直线y=﹣x+b与x轴的交点坐标为(b,0),与y轴交点坐标为(0,b),
AB===b,
当b>0时,b+b+b=16,得b=4,
此时,S△AOB=OA?OB=××4=,
即坐标三角形面积为;
当b<0时,﹣b﹣b﹣b=16,得b=﹣4,
此时,S△AOB=OA?OB=××4=,
即坐标三角形面积为.
综上,当函数y=﹣x+b的坐标三角形周长为16时,面积为.
22.已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= 2 ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=﹣x+b,求n的值.
解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x﹣2+b,
由题意,得0=0﹣2+b,解得b=2.故答案为2;
(2)∵当x=0时,y=4,∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,∴(0,4)在函数y=x+b图象上.∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(﹣4,0).
∵y2=kx﹣4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx﹣4的图象经过点(4,0),则0=4k+4,∴k=﹣1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=﹣b,
∴y1=x+b图象与x轴交于点A(﹣b,0).
如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=,
∴y3=﹣x+b图象与x轴交于点C(,0).
如图,∵CO=,∴tan∠ACB==,∴∠ACB=60°.
∴n°=180°﹣∠ACB﹣∠BAC=75°.即n的值为75.
23.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
(1)求AB、BD的长度,并证明△ABD是直角三角形;
(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;
(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.
解:(1)令x=0,y=4,令y=0,则﹣x+4=0,
解得x=3,所以,A(0,4),B(3,0),
由勾股定理得,AB==5,BD==10,
过点D作DH⊥y轴于H,DH=11,AH=2,
由勾股定理得,AD===,
∵AB2=25,BD2=100,∴AB2+BD2=AD2,
∴△ABD是直角三角形;
(2)设OC长为x,由等腰三角形以及勾股定理得到x2+42=(11﹣x)2+62,
解得x=,所以,C(,0);
(3)设t秒时相遇,由题意得,t+t=5+10,解得t=7.5,
点P在AB上时,0≤t≤5,PB=5﹣t,BQ=10﹣t,
PQ===,
所以,y=,
点P、Q都在BD上重合前,5<t≤7.5,PQ=5+10﹣t﹣t=15﹣2t,
重合后,7.5<t≤10,PQ=t+t﹣5﹣10=2t﹣15,
所以,y=2t﹣15,
点Q在AB上时,10<t≤15,PB=t﹣5,BQ=t﹣10,
PQ===,
所以,y=.
