第1章导数及其应用专解3 求函数的单调区间-2020-2021学年人教A版高中数学选修2-2专题考点训练(必备知识点)Word
文档属性
| 名称 | 第1章导数及其应用专解3 求函数的单调区间-2020-2021学年人教A版高中数学选修2-2专题考点训练(必备知识点)Word |
|
|
| 格式 | zip | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 14:56:56 | ||
图片预览




文档简介
【必备知识点】
1.函数的单调性与导数的关系
我们知道,如果函数在某个区间是增函数或减函数,那么就说在这一区间具有单调性.
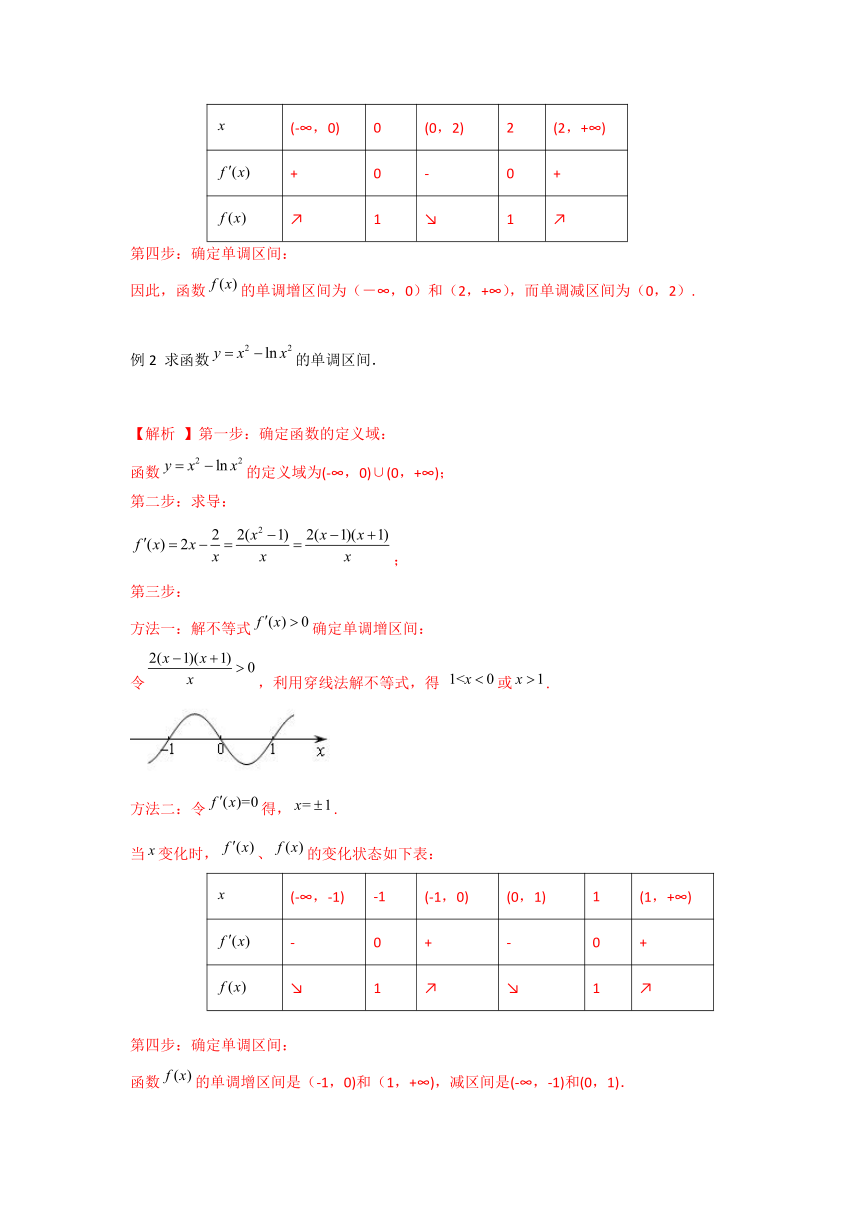
已知函数的图象如图所示,
由函数的单调性易知,当时,是减函数;当时,是增函数.现在我们看看各个单调区间内任意一点的切线情况:
考虑到曲线的在某点处切线的斜率就是函数在改点的导数值,从图象可以看到:
在区间(-∞,2)内,任意一点的切线的斜率为负,即时,为减函数.
在区间(2,+∞)内,任意一点的切线的斜率为正,即时,为增函数.
导数的符号与函数的单调性:
一般地,设函数在某个区间内有导数,则在这个区间上,
(1)若,则在这个区间上为增函数;
(2)若,则在这个区间上为减函数;
(3)若恒有,则在这一区间上为常函数.
反之,若在某区间上单调递增,则在该区间上有恒成立(但不恒等于0);若在某区间上单调递减,则在该区间上有恒成立(但不恒等于0).
2.利用导数研究函数的单调性
利用导数判断函数单调性的基本方法:
设函数在区间(,b)内可导,
(1)如果恒有,则函数在(,b)内为增函数;
(2)如果恒有,则函数在(,b)内为减函数;
(3)如果恒有,则函数在(,b)内为常数函数.
【典例展示】
例1.
确定函数的单调区间.
【解析】第一步:确定函数的定义域:
的定义域为R;
第二步:求导:
,
第三步:
方法一:解不等式确定函数的单调增区间:
令,解得<0或>2,
则函数在<0或>2时是增函数;
方法二:列表法:
令,解得=0或=2.
当变化时,、的变化状态如下表:
(-∞,0)
0
(0,2)
2
(2,+∞)
+
0
-
0
+
↗
1
↘
1
↗
第四步:确定单调区间:
因此,函数的单调增区间为(-∞,0)和(2,+∞),而单调减区间为(0,2).
例2
求函数的单调区间.
【解析
】第一步:确定函数的定义域:
函数的定义域为(-∞,0)∪(0,+∞);
第二步:求导:
;
第三步:
方法一:解不等式确定单调增区间:
令,利用穿线法解不等式,得或.
方法二:令得,.
当变化时,、的变化状态如下表:
(-∞,-1)
-1
(-1,0)
(0,1)
1
(1,+∞)
-
0
+
-
0
+
↘
1
↗
↘
1
↗
第四步:确定单调区间:
函数的单调增区间是(-1,0)和(1,+∞),减区间是(-∞,-1)和(0,1).
例3.
已知函数,求导函数,并确定的单调区间.
【解析】第一步:确定函数的定义域:
的定义域为;
第二步:求导:
;
第三步:解不等式,求单调增区间:
令,得,
同解于.
当,即,不等式的解为;
当,即,不等式的解为空集;
当,即,不等式的解为.
综上,当时,的单调增区间为,单调减区间为;
当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为.
例4.证明不等式,其中.
【解析】设,
,
,
在内为单调增函数.
又,当时,,
即,.
【思路总结与方法】
思路:求函数的单调区间即为求使其导函数为正(或负)的x值的范围,先正确求出函数的导函数,然后再在函数的定义域内解导函数的不等式即可。
解题步骤:
①根据所给函数的特点,确定函数的定义域.
②利用导数运算法则求出函数的导数.
③在函数定义域内,解不等式,得函数的单调递增区间;解不等式,得函数的单调递减区间.
【巩固练习】
1.求下列函数的单调区间:
(1);
(2).
【解析】(1)第一步:确定函数的定义域:
该函数的定义域为R;
第二步:求导:
;
第三步:解不等式:
令32―4+1>0,解得>1或;
第四步:确定单调区间:
因此,函数的单调递增区间为(1,+∞)和,单调减区间为.
(2)函数的定义域为(0,+∞),
,
令,即,等价于
解得,
∴的单调递增区间为,单调递减区间为.
2.求下列函数的单调区间:
(1);
(2).
【解析】(1)第一步:确定函数的定义域:
该函数的定义域为;
第二步:求导:
;
第三步:列表:
令,解得=3.
实数2和3将数轴分成3个子区间,在各个子区间内,、的变化状态如下表:
3
0
+
…
第四步:确定单调区间:
所以,该函数的单调减区间是和,单调增区间是.
(2)令.
解得或,∵0≤≤2π,解得,,.
0
π
…
+
0
-
0
-
0
+
…
…
…
…
…
则区间[0,2π]被分成三个子区间,、的变化状态如下表所示:
所以该函数的单调递增区间为和,单调递减区间为
3.已知函数,求函数的单调区间并说明其单调性.
【答案】该函数的定义域为,
,
令,即,等价于,讨论如下:
当时,解不等式①得,由于,故无解;
当时,解得,结合函数的定义域,可得.
综上所述,当时,的单调增区间是,无减区间;
当时,的单调减区间是,无增区间;
当时,的单调增区间是,减区间为.
4.当时,求证:函数是单调递减函数.
【答案】
,∴,,∴
故函数在上是单调递减函数.
【课后练习】
一、选择题
1.下列命题成立的是(
)
A.若在(,)内是增函数,则对任何∈(,),都有>0
B.若在(,)内对任何都有>0,则在(,)上是增函数
C.若在(,)内是单调函数,则必存在
D.若在(,)上都存在,则必为单调函数
3.
函数=(-3)的单调递增区间是(
)
A.(-∞,2)
B.(0,3)
C.(1,4)
D.(2,+∞)
4.函数的单调递增区间是(
)
A.
B.
C.
D.(,e)
5.
设在(0,+∞)内单调递增,,
则p是q的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.对于R上可导的任意函数,若满足(-1)≥0,则必有(
)
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)≤2f(1)
C.f(0)+f(2)≥2f(1)
D.f(0)+f(2)>2f(1)
7.设函数在R上的导函数为,且,下面的不等式在R内恒成立的是(
)
A.
B.
C.
D.
二、填空题
8.函数的单调减区间为
.
9.函数y=sin+cos,∈(-π,π)的单调增区间是____________.
10.函数y=ln(2--2)的单调递减区间为__________.
三、解答题
11.已知函数=3+2+c+d的图像经过点P(0,2),且在点M(-1,f(-1))处的切线方程为6-y+7=0.
(1)求函数y=的解析式;(2)求函数y=的单调区间.
【答案与解析】
1.
【答案】B.
【解析】 若在(,)内是增函数,则≥0,故A错;在(,)内是单调函数与是否存在无必然联系,故C错;=2在(,)上的导数为=0存在,但无单调性,故D错.
3.
【答案】D.
【解析】=(-3)′+(-3)(
)′=(-2)
,
令>0,解得>2,故选D.
4.
【答案】C.
【解析】,令,即,解得,所以选C.
5.
【答案】B.
【解析】由题意知在(0,+∞)上恒成立,
则在∈(0,+∞)上恒成立。
当∈(0,+∞)时,,
则的最大值要小于-5,不妨设为c,
∴m≥c不可能推出m≥-5。但由m≥-5,可以推出m≥c。故B正确。
6.
【答案】C
【解析】由(-1)≥0得在[1,+∞)上单调递增,在(-∞,1]上单调递减或恒为常数,
故f(0)+f(2)≥2f(1).故应选C.
7.
【答案】A.
【解析】由>0时,。
令,则。
∵,∴在(0,+∞)上为增函数。
当<0时,。
令,则。
∴在(-∞,0)上为减函数,∴,
∴在R上恒成立,且≠0时,。
即,∴在∈R且≠0时恒成立。
把=0代入得,
∴在R上恒成立。
8.
【答案】(-1,11)
【解析】,
由得单调减区间为。
亦可填写闭区间或半开半闭区间。
9.【答案】和
【解析】
y′=cos,当-π<<-时,cos<0,∴y′=cos>0,
当0<<
时,cos>0,∴y′=cos>0.
10.
【答案】
(-∞,-1)
【解析】
函数y=ln(2--2)的定义域为(2,+∞)∪(-∞,-1),
令=2--2,=2-1<0,得<,
∴函数y=ln(2--2)的单调减区间为(-∞,-1).
11.
【解析】
1.函数的单调性与导数的关系
我们知道,如果函数在某个区间是增函数或减函数,那么就说在这一区间具有单调性.
已知函数的图象如图所示,
由函数的单调性易知,当时,是减函数;当时,是增函数.现在我们看看各个单调区间内任意一点的切线情况:
考虑到曲线的在某点处切线的斜率就是函数在改点的导数值,从图象可以看到:
在区间(-∞,2)内,任意一点的切线的斜率为负,即时,为减函数.
在区间(2,+∞)内,任意一点的切线的斜率为正,即时,为增函数.
导数的符号与函数的单调性:
一般地,设函数在某个区间内有导数,则在这个区间上,
(1)若,则在这个区间上为增函数;
(2)若,则在这个区间上为减函数;
(3)若恒有,则在这一区间上为常函数.
反之,若在某区间上单调递增,则在该区间上有恒成立(但不恒等于0);若在某区间上单调递减,则在该区间上有恒成立(但不恒等于0).
2.利用导数研究函数的单调性
利用导数判断函数单调性的基本方法:
设函数在区间(,b)内可导,
(1)如果恒有,则函数在(,b)内为增函数;
(2)如果恒有,则函数在(,b)内为减函数;
(3)如果恒有,则函数在(,b)内为常数函数.
【典例展示】
例1.
确定函数的单调区间.
【解析】第一步:确定函数的定义域:
的定义域为R;
第二步:求导:
,
第三步:
方法一:解不等式确定函数的单调增区间:
令,解得<0或>2,
则函数在<0或>2时是增函数;
方法二:列表法:
令,解得=0或=2.
当变化时,、的变化状态如下表:
(-∞,0)
0
(0,2)
2
(2,+∞)
+
0
-
0
+
↗
1
↘
1
↗
第四步:确定单调区间:
因此,函数的单调增区间为(-∞,0)和(2,+∞),而单调减区间为(0,2).
例2
求函数的单调区间.
【解析
】第一步:确定函数的定义域:
函数的定义域为(-∞,0)∪(0,+∞);
第二步:求导:
;
第三步:
方法一:解不等式确定单调增区间:
令,利用穿线法解不等式,得或.
方法二:令得,.
当变化时,、的变化状态如下表:
(-∞,-1)
-1
(-1,0)
(0,1)
1
(1,+∞)
-
0
+
-
0
+
↘
1
↗
↘
1
↗
第四步:确定单调区间:
函数的单调增区间是(-1,0)和(1,+∞),减区间是(-∞,-1)和(0,1).
例3.
已知函数,求导函数,并确定的单调区间.
【解析】第一步:确定函数的定义域:
的定义域为;
第二步:求导:
;
第三步:解不等式,求单调增区间:
令,得,
同解于.
当,即,不等式的解为;
当,即,不等式的解为空集;
当,即,不等式的解为.
综上,当时,的单调增区间为,单调减区间为;
当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为.
例4.证明不等式,其中.
【解析】设,
,
,
在内为单调增函数.
又,当时,,
即,.
【思路总结与方法】
思路:求函数的单调区间即为求使其导函数为正(或负)的x值的范围,先正确求出函数的导函数,然后再在函数的定义域内解导函数的不等式即可。
解题步骤:
①根据所给函数的特点,确定函数的定义域.
②利用导数运算法则求出函数的导数.
③在函数定义域内,解不等式,得函数的单调递增区间;解不等式,得函数的单调递减区间.
【巩固练习】
1.求下列函数的单调区间:
(1);
(2).
【解析】(1)第一步:确定函数的定义域:
该函数的定义域为R;
第二步:求导:
;
第三步:解不等式:
令32―4+1>0,解得>1或;
第四步:确定单调区间:
因此,函数的单调递增区间为(1,+∞)和,单调减区间为.
(2)函数的定义域为(0,+∞),
,
令,即,等价于
解得,
∴的单调递增区间为,单调递减区间为.
2.求下列函数的单调区间:
(1);
(2).
【解析】(1)第一步:确定函数的定义域:
该函数的定义域为;
第二步:求导:
;
第三步:列表:
令,解得=3.
实数2和3将数轴分成3个子区间,在各个子区间内,、的变化状态如下表:
3
0
+
…
第四步:确定单调区间:
所以,该函数的单调减区间是和,单调增区间是.
(2)令.
解得或,∵0≤≤2π,解得,,.
0
π
…
+
0
-
0
-
0
+
…
…
…
…
…
则区间[0,2π]被分成三个子区间,、的变化状态如下表所示:
所以该函数的单调递增区间为和,单调递减区间为
3.已知函数,求函数的单调区间并说明其单调性.
【答案】该函数的定义域为,
,
令,即,等价于,讨论如下:
当时,解不等式①得,由于,故无解;
当时,解得,结合函数的定义域,可得.
综上所述,当时,的单调增区间是,无减区间;
当时,的单调减区间是,无增区间;
当时,的单调增区间是,减区间为.
4.当时,求证:函数是单调递减函数.
【答案】
,∴,,∴
故函数在上是单调递减函数.
【课后练习】
一、选择题
1.下列命题成立的是(
)
A.若在(,)内是增函数,则对任何∈(,),都有>0
B.若在(,)内对任何都有>0,则在(,)上是增函数
C.若在(,)内是单调函数,则必存在
D.若在(,)上都存在,则必为单调函数
3.
函数=(-3)的单调递增区间是(
)
A.(-∞,2)
B.(0,3)
C.(1,4)
D.(2,+∞)
4.函数的单调递增区间是(
)
A.
B.
C.
D.(,e)
5.
设在(0,+∞)内单调递增,,
则p是q的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.对于R上可导的任意函数,若满足(-1)≥0,则必有(
)
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)≤2f(1)
C.f(0)+f(2)≥2f(1)
D.f(0)+f(2)>2f(1)
7.设函数在R上的导函数为,且,下面的不等式在R内恒成立的是(
)
A.
B.
C.
D.
二、填空题
8.函数的单调减区间为
.
9.函数y=sin+cos,∈(-π,π)的单调增区间是____________.
10.函数y=ln(2--2)的单调递减区间为__________.
三、解答题
11.已知函数=3+2+c+d的图像经过点P(0,2),且在点M(-1,f(-1))处的切线方程为6-y+7=0.
(1)求函数y=的解析式;(2)求函数y=的单调区间.
【答案与解析】
1.
【答案】B.
【解析】 若在(,)内是增函数,则≥0,故A错;在(,)内是单调函数与是否存在无必然联系,故C错;=2在(,)上的导数为=0存在,但无单调性,故D错.
3.
【答案】D.
【解析】=(-3)′+(-3)(
)′=(-2)
,
令>0,解得>2,故选D.
4.
【答案】C.
【解析】,令,即,解得,所以选C.
5.
【答案】B.
【解析】由题意知在(0,+∞)上恒成立,
则在∈(0,+∞)上恒成立。
当∈(0,+∞)时,,
则的最大值要小于-5,不妨设为c,
∴m≥c不可能推出m≥-5。但由m≥-5,可以推出m≥c。故B正确。
6.
【答案】C
【解析】由(-1)≥0得在[1,+∞)上单调递增,在(-∞,1]上单调递减或恒为常数,
故f(0)+f(2)≥2f(1).故应选C.
7.
【答案】A.
【解析】由>0时,。
令,则。
∵,∴在(0,+∞)上为增函数。
当<0时,。
令,则。
∴在(-∞,0)上为减函数,∴,
∴在R上恒成立,且≠0时,。
即,∴在∈R且≠0时恒成立。
把=0代入得,
∴在R上恒成立。
8.
【答案】(-1,11)
【解析】,
由得单调减区间为。
亦可填写闭区间或半开半闭区间。
9.【答案】和
【解析】
y′=cos,当-π<<-时,cos<0,∴y′=cos>0,
当0<<
时,cos>0,∴y′=cos>0.
10.
【答案】
(-∞,-1)
【解析】
函数y=ln(2--2)的定义域为(2,+∞)∪(-∞,-1),
令=2--2,=2-1<0,得<,
∴函数y=ln(2--2)的单调减区间为(-∞,-1).
11.
【解析】
