第1章导数及其应用专解5 求函数的最值-2020-2021学年人教A版高中数学选修2-2专题考点训练(必备知识点) Word
文档属性
| 名称 | 第1章导数及其应用专解5 求函数的最值-2020-2021学年人教A版高中数学选修2-2专题考点训练(必备知识点) Word |

|
|
| 格式 | zip | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 14:59:28 | ||
图片预览




文档简介
【必备知识点】
1.函数的最值
函数的最大值与最小值定理
若函数在闭区间上连续,则在上必有最大值和最小值;在开区间
2.最值与极值的区别与联系
①函数的最大值和最小值是比较整个定义域上的函数值得出的(具有绝对性),是整个定义域上的整体性概念.
最大值是函数在整个定义域上所有函数值中的最大值;最小值是函数在整个定义域上所有函数值中的最小值.
函数的极大值与极小值是比较极值点附近两侧的函数值而得出的(具有相对性),是局部的概念;
②极值可以有多个,最大(小)值若存在只有一个;极值只能在区间内取得,不能在区间端点取得;最大(小)值可能是某个极大(小)值,也可能是区间端点处的函数值;
③有极值的函数不一定有最值,有最值的函数未必有极值,极值可能成为最值.
3.函数极值与最值的简单应用
①不等式恒成立,求参数范围问题
一些含参不等式,一般形如,
若能隔离参数,即可化为:的形式.若其恒成立,则可转化成,从而转化为求函数的最值问题.
若不能隔离参数,就是求含参函数
的最小值
,使.
所以仍为求函数的最值问题,只是再求最值时可能需要对参数进行分类讨论.
②证不等式问题
当所要证的不等式中只含一个未知数时,一般形式为,则可化为,一般设,然后求的最小值,证即可.
所以证不等式问题也可转化为求函数最小值问题.
③两曲线的交点个数问题(方程解的个数问题)
一般可转化为方程的问题,即的解的个数问题,
我们可以设,然后求出的极大值、极小值,根据解的个数讨论极大值、极小值与0的大小关系即可.
所以此类问题可转化为求函数的极值问题.
【典例展示】
例1.
求函数在区间[-1,2]上的最大值与最小值。
【解析】
,
-1
0
2
+
+
0
-
0
+
+
-2
1
1
又,,
结合上表可知,当x=-1时,f(x)取最小值-2;当x=0或2时,f(x)取最大值1.
∴
函数在区间[-1,2]上的最大值为1,最小值为-2.
【总结升华】解题格式要求:(1)对于分解因式,写出相应方程的根;(2)列表格,表格反映出随的变化情况,必须列出极值点,若求最值时,还要列出端点的函数值;(3)一般要注明x取何值时取得最大最小值.
例2:求函数,x∈[-3,2]
的最值.
【解析】,
由得x=―1,0,1.
∵f(-3)=-60,f(-1)=f(1)=4,f(0)=3,
f(2)=-5,
经比较可得:
当x=―3时,有最小值―60;
当x=―1时或1时,有最大值4.
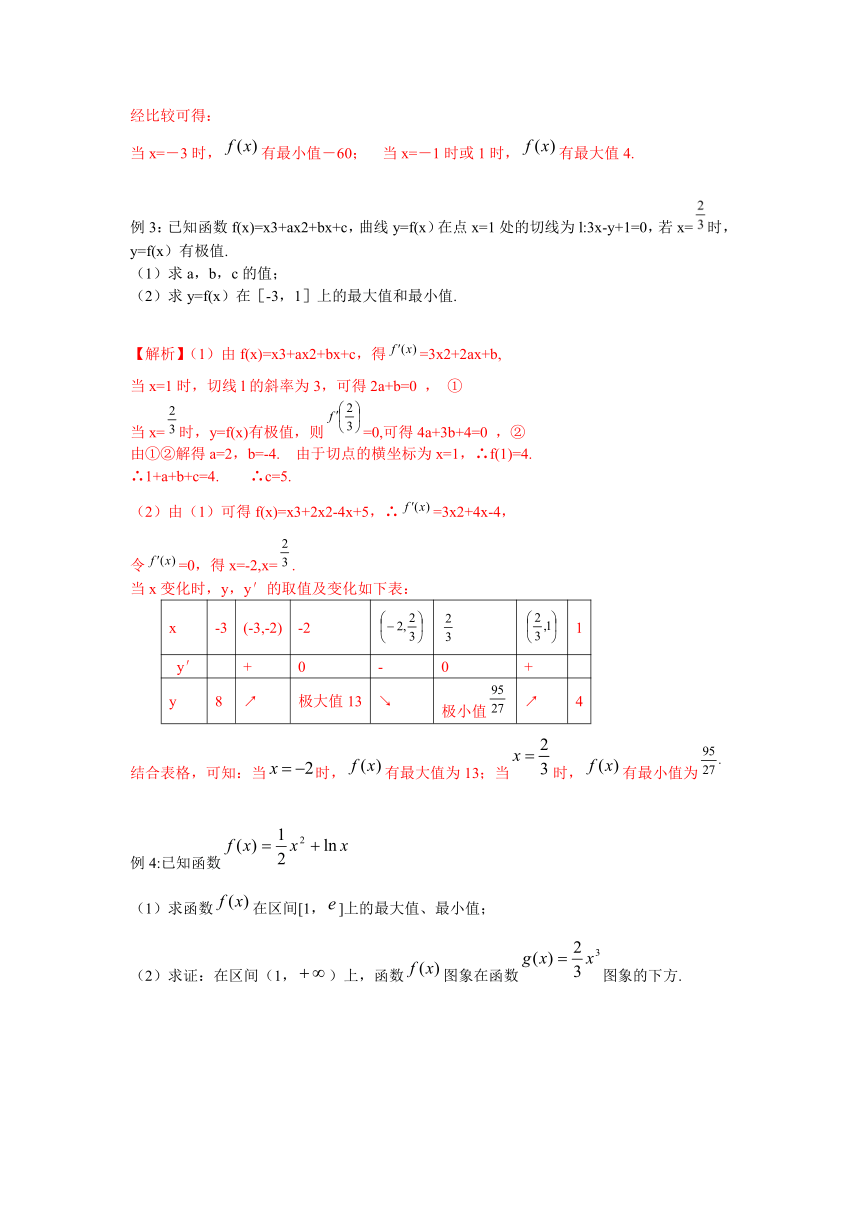
例3:已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线为l:3x-y+1=0,若x=时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
【解析】(1)由f(x)=x3+ax2+bx+c,得=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b=0
,
①
当x=时,y=f(x)有极值,则=0,可得4a+3b+4=0
,②
由①②解得a=2,b=-4.
由于切点的横坐标为x=1,∴f(1)=4.?
∴1+a+b+c=4.
∴c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,∴=3x2+4x-4,
令=0,得x=-2,x=.
当x变化时,y,y′的取值及变化如下表:
x
-3
(-3,-2)
-2
1
y′
+
0
-
0
+
y
8
↗
极大值13
↘
极小值
↗
4
结合表格,可知:当时,有最大值为13;当时,有最小值为
例4:已知函数
(1)求函数在区间[1,]上的最大值、最小值;
(2)求证:在区间(1,)上,函数图象在函数图象的下方.
【解析】(1)=,令,得,
当[1,]时,,则在区间[1,]上是增函数,
∴
当时,有最小值;当时,有最大值.
(2)设=,则,
∵
,
,
∴
在区间(1,)上是减函数,
又∵
,
∴
,即,,
∴在区间(1,)上,函数图象在函数图象的下方.
例5:设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
【解析】
令g(x)=(x+1)ln(x+1)-ax,
对函数g(x)求导数:g′(x)=ln(x+1)+1-a
令g′(x)=0,解得x=ea-1-1,
(i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,
又g(0)=0,所以对x≥0,都有g(x)≥g(0),
即当a≤1时,对于所有x≥0,都有f(x)≥ax.
(ii)当a>1时,对于0<x<ea-1-1,g′(x)<0,所以g(x)在(0,ea-1-1)是减函数,
又g(0)=0,所以对0<x<ea-1-1,都有g(x)<g(0),
即当a>1时,对所有的x≥0,都有f(x)≥ax成立.
综上,a的取值范围是(-∞,1].
【思路总结与方法】
思路:解决本专题的依据是在闭区间上,函数的最值一定在极值点或端点处取得,故可通过比较函数在极值点和端点处的函数值得大小求得最值,若在其他区间类型上,则可结合函数的单调性求解.
解题步骤:
①求出导数,令,的.
②求出.和定义域区间端点函数值.
③比较和,最大的即为最大值,最小的即为最小值.
【巩固练习】
1.求函数y=x4―2x2+5在区间[―2,2]上的最大值与最小值。
【解析】
先求导数,得y'=4x3―4x。
令y'=0即4x3―4x=0,
解得x1=―1,x2=0,x3=1。
当x变化时,y',y的变化情况如下表:
x
-2
(―2,―1)
-1
(-1,0)
0
(0,1)
1
(1,2)
2
y'
-
0
+
0
-
0
+
y
13
4
5
4
13
从上表知,当x=±2时,函数有最大值13;当x=±1时,函数有最小值4。
2.求函数,x∈[0,2]的最值.
【解析】,令,
化简为x2+x―2=0,解得x1=―2(舍去),x2=1.
∵,又,,
∴为函数在[0,2]上的最小值,为函数在[0,2]上的最大值.
3.设函数。
(1)当a=1时,求的单调区间;
(2)若中(0,1]上的最大值为,求a的值.
【解析】
函数的定义域为(0,2),
,
(1)当a=1时,,所以的单调递增区间为,单调递减区间为;
(2)当a∈(0,1]时,,
即在(0,1]上单调递增,故在(0,1]上的最大值为,因此.
4.求证:当x>0时,.
【答案】
设,
,
,,则函数在上是单调增函数,
∴当x>0时,,
即x>0时,.
5.已知,是否存在实数使得方程在区间内有且只有两个不等的实数根?若存在,求出的取值范围;若不存在,说明理由。
【答案】
方程等价于方程
设则
当时,是减函数;
当时,是增函数.
方程在区间内分别有唯一实数根,
而在区间内没有实数根,
所以存在唯一的自然数使得方程在区间内有且只有两个不同的实数根.
6.已知函数。
(1)若图象有与x轴平行的切线,求b的取值范围;
(2)若在x=1处取得极值,且x∈[―1,2]时,恒成立,求c的取值范围。
【解析】(1),的图象上有与x轴平行的切线,则有实数解,
即方程3x2―x+b=0有实数解,∴Δ=1―2b≥0,解得。
(2)由题意知x=1是方程3x2―x+b=0的一个根,
设另一根为x0,则,∴,
∴,。
当,;
当时,;
当x∈(1,2)时,。
∴当时,有极大值。
又,。
∴当x∈[-1,2]时,的最大值为。
又∵当x∈[-1,2]时,恒成立,
∴c2>2+c,解得c<-1或c>2。
故c的取值范围是(-∞,-1)∪(2,+∞)。
【课后练习】
一、选择题
1.函数f(x)=2
x3-12
x2+3在区间[-1,2]上的最大、最小值的情况是(
).
A.最大值为3,最小值为-29
B.最大值为3,最小值为-61
C.最大值为-29,最小值为-61
D.以上答案都不对
2.下列结论正确的是(
)
A.若x0是在[a,b]上的极大值点,则是在[a,b]上的最大值
B.若x0是在(a,b)上的极大值点,则是在[a,b]上的最小值
C.若x0是在[a,b]上唯一极大值点,则是在[a,b]上的最大值
D.若x0是在(a,b)上的极大值点,且在(a,b)上无极小值,则是在[a,b]上的最大值
3.已知函数y=―x2―2x+3在区间[a,2]上的最大值为,则a等于(
)
A.
B.
C.
D.或
二、填空题
4.函数y=xex的最小值为________.
5.若函数在x=1处取得极值,则a=________.
6.函数在区间[―3,3]上的最小值是________.
三、解答题
7.求函数,的最值.
8.a为常数,求函数的最大值.
【答案与解析】
1.
【答案】A
【解析】f′(x)=6
x2-24
x,令f′(x)=0得
x1=0,x2=4
x2=4[-1,2],舍去.
2.【答案】D
【解析】
若在(a,b)上只有一个极值且为极大值时,则在[a,b]上
为最大值.
3【答案】C
【解析】.令,得x=-1.
当a≤―1时,最大值为4,不合题意;
当―1<a<2时,在[a,2]上是减函数,最大,,,(舍).
4.
【答案】
【解析】
∵,
∴当x>―1时,y'>0,当x<―1时,y'<0.
∴x=-1时,.
5.
【答案】
3
【解析】
,
.
6.【答案】-16
【解析】
由,解得x=±2.
∵,
,
,
,
∴的最小值为―16.
7.
【解析】
,
令,得,又,
∴2x∈[-π,π].
∴,即.
∴函数在上的两个极值分别为
,.
又在区间端点的取值为,.
比较以上函数值可得,.
8.【解析】
.
若a≤0,则,x∈[0,1],函数单调递减.
∴当x=0时,有最大值,
若a>0,则令,解得.
∵x∈[0,1],则只考虑的情况.
当x变化时,,的变化情况如下表所示:
x
0
0
+
0
-
极大值
(1),即0<a<1,当时,有最大值.
(2),即a≥1,当x=1时,有最大值.
综上,当a≤0,x=0时,有最大值0;
当0<a<1,时,有最大值;
当a≥1,x=1时,有最大值3a―1.
1.函数的最值
函数的最大值与最小值定理
若函数在闭区间上连续,则在上必有最大值和最小值;在开区间
2.最值与极值的区别与联系
①函数的最大值和最小值是比较整个定义域上的函数值得出的(具有绝对性),是整个定义域上的整体性概念.
最大值是函数在整个定义域上所有函数值中的最大值;最小值是函数在整个定义域上所有函数值中的最小值.
函数的极大值与极小值是比较极值点附近两侧的函数值而得出的(具有相对性),是局部的概念;
②极值可以有多个,最大(小)值若存在只有一个;极值只能在区间内取得,不能在区间端点取得;最大(小)值可能是某个极大(小)值,也可能是区间端点处的函数值;
③有极值的函数不一定有最值,有最值的函数未必有极值,极值可能成为最值.
3.函数极值与最值的简单应用
①不等式恒成立,求参数范围问题
一些含参不等式,一般形如,
若能隔离参数,即可化为:的形式.若其恒成立,则可转化成,从而转化为求函数的最值问题.
若不能隔离参数,就是求含参函数
的最小值
,使.
所以仍为求函数的最值问题,只是再求最值时可能需要对参数进行分类讨论.
②证不等式问题
当所要证的不等式中只含一个未知数时,一般形式为,则可化为,一般设,然后求的最小值,证即可.
所以证不等式问题也可转化为求函数最小值问题.
③两曲线的交点个数问题(方程解的个数问题)
一般可转化为方程的问题,即的解的个数问题,
我们可以设,然后求出的极大值、极小值,根据解的个数讨论极大值、极小值与0的大小关系即可.
所以此类问题可转化为求函数的极值问题.
【典例展示】
例1.
求函数在区间[-1,2]上的最大值与最小值。
【解析】
,
-1
0
2
+
+
0
-
0
+
+
-2
1
1
又,,
结合上表可知,当x=-1时,f(x)取最小值-2;当x=0或2时,f(x)取最大值1.
∴
函数在区间[-1,2]上的最大值为1,最小值为-2.
【总结升华】解题格式要求:(1)对于分解因式,写出相应方程的根;(2)列表格,表格反映出随的变化情况,必须列出极值点,若求最值时,还要列出端点的函数值;(3)一般要注明x取何值时取得最大最小值.
例2:求函数,x∈[-3,2]
的最值.
【解析】,
由得x=―1,0,1.
∵f(-3)=-60,f(-1)=f(1)=4,f(0)=3,
f(2)=-5,
经比较可得:
当x=―3时,有最小值―60;
当x=―1时或1时,有最大值4.
例3:已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线为l:3x-y+1=0,若x=时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
【解析】(1)由f(x)=x3+ax2+bx+c,得=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b=0
,
①
当x=时,y=f(x)有极值,则=0,可得4a+3b+4=0
,②
由①②解得a=2,b=-4.
由于切点的横坐标为x=1,∴f(1)=4.?
∴1+a+b+c=4.
∴c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,∴=3x2+4x-4,
令=0,得x=-2,x=.
当x变化时,y,y′的取值及变化如下表:
x
-3
(-3,-2)
-2
1
y′
+
0
-
0
+
y
8
↗
极大值13
↘
极小值
↗
4
结合表格,可知:当时,有最大值为13;当时,有最小值为
例4:已知函数
(1)求函数在区间[1,]上的最大值、最小值;
(2)求证:在区间(1,)上,函数图象在函数图象的下方.
【解析】(1)=,令,得,
当[1,]时,,则在区间[1,]上是增函数,
∴
当时,有最小值;当时,有最大值.
(2)设=,则,
∵
,
,
∴
在区间(1,)上是减函数,
又∵
,
∴
,即,,
∴在区间(1,)上,函数图象在函数图象的下方.
例5:设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
【解析】
令g(x)=(x+1)ln(x+1)-ax,
对函数g(x)求导数:g′(x)=ln(x+1)+1-a
令g′(x)=0,解得x=ea-1-1,
(i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,
又g(0)=0,所以对x≥0,都有g(x)≥g(0),
即当a≤1时,对于所有x≥0,都有f(x)≥ax.
(ii)当a>1时,对于0<x<ea-1-1,g′(x)<0,所以g(x)在(0,ea-1-1)是减函数,
又g(0)=0,所以对0<x<ea-1-1,都有g(x)<g(0),
即当a>1时,对所有的x≥0,都有f(x)≥ax成立.
综上,a的取值范围是(-∞,1].
【思路总结与方法】
思路:解决本专题的依据是在闭区间上,函数的最值一定在极值点或端点处取得,故可通过比较函数在极值点和端点处的函数值得大小求得最值,若在其他区间类型上,则可结合函数的单调性求解.
解题步骤:
①求出导数,令,的.
②求出.和定义域区间端点函数值.
③比较和,最大的即为最大值,最小的即为最小值.
【巩固练习】
1.求函数y=x4―2x2+5在区间[―2,2]上的最大值与最小值。
【解析】
先求导数,得y'=4x3―4x。
令y'=0即4x3―4x=0,
解得x1=―1,x2=0,x3=1。
当x变化时,y',y的变化情况如下表:
x
-2
(―2,―1)
-1
(-1,0)
0
(0,1)
1
(1,2)
2
y'
-
0
+
0
-
0
+
y
13
4
5
4
13
从上表知,当x=±2时,函数有最大值13;当x=±1时,函数有最小值4。
2.求函数,x∈[0,2]的最值.
【解析】,令,
化简为x2+x―2=0,解得x1=―2(舍去),x2=1.
∵,又,,
∴为函数在[0,2]上的最小值,为函数在[0,2]上的最大值.
3.设函数。
(1)当a=1时,求的单调区间;
(2)若中(0,1]上的最大值为,求a的值.
【解析】
函数的定义域为(0,2),
,
(1)当a=1时,,所以的单调递增区间为,单调递减区间为;
(2)当a∈(0,1]时,,
即在(0,1]上单调递增,故在(0,1]上的最大值为,因此.
4.求证:当x>0时,.
【答案】
设,
,
,,则函数在上是单调增函数,
∴当x>0时,,
即x>0时,.
5.已知,是否存在实数使得方程在区间内有且只有两个不等的实数根?若存在,求出的取值范围;若不存在,说明理由。
【答案】
方程等价于方程
设则
当时,是减函数;
当时,是增函数.
方程在区间内分别有唯一实数根,
而在区间内没有实数根,
所以存在唯一的自然数使得方程在区间内有且只有两个不同的实数根.
6.已知函数。
(1)若图象有与x轴平行的切线,求b的取值范围;
(2)若在x=1处取得极值,且x∈[―1,2]时,恒成立,求c的取值范围。
【解析】(1),的图象上有与x轴平行的切线,则有实数解,
即方程3x2―x+b=0有实数解,∴Δ=1―2b≥0,解得。
(2)由题意知x=1是方程3x2―x+b=0的一个根,
设另一根为x0,则,∴,
∴,。
当,;
当时,;
当x∈(1,2)时,。
∴当时,有极大值。
又,。
∴当x∈[-1,2]时,的最大值为。
又∵当x∈[-1,2]时,恒成立,
∴c2>2+c,解得c<-1或c>2。
故c的取值范围是(-∞,-1)∪(2,+∞)。
【课后练习】
一、选择题
1.函数f(x)=2
x3-12
x2+3在区间[-1,2]上的最大、最小值的情况是(
).
A.最大值为3,最小值为-29
B.最大值为3,最小值为-61
C.最大值为-29,最小值为-61
D.以上答案都不对
2.下列结论正确的是(
)
A.若x0是在[a,b]上的极大值点,则是在[a,b]上的最大值
B.若x0是在(a,b)上的极大值点,则是在[a,b]上的最小值
C.若x0是在[a,b]上唯一极大值点,则是在[a,b]上的最大值
D.若x0是在(a,b)上的极大值点,且在(a,b)上无极小值,则是在[a,b]上的最大值
3.已知函数y=―x2―2x+3在区间[a,2]上的最大值为,则a等于(
)
A.
B.
C.
D.或
二、填空题
4.函数y=xex的最小值为________.
5.若函数在x=1处取得极值,则a=________.
6.函数在区间[―3,3]上的最小值是________.
三、解答题
7.求函数,的最值.
8.a为常数,求函数的最大值.
【答案与解析】
1.
【答案】A
【解析】f′(x)=6
x2-24
x,令f′(x)=0得
x1=0,x2=4
x2=4[-1,2],舍去.
2.【答案】D
【解析】
若在(a,b)上只有一个极值且为极大值时,则在[a,b]上
为最大值.
3【答案】C
【解析】.令,得x=-1.
当a≤―1时,最大值为4,不合题意;
当―1<a<2时,在[a,2]上是减函数,最大,,,(舍).
4.
【答案】
【解析】
∵,
∴当x>―1时,y'>0,当x<―1时,y'<0.
∴x=-1时,.
5.
【答案】
3
【解析】
,
.
6.【答案】-16
【解析】
由,解得x=±2.
∵,
,
,
,
∴的最小值为―16.
7.
【解析】
,
令,得,又,
∴2x∈[-π,π].
∴,即.
∴函数在上的两个极值分别为
,.
又在区间端点的取值为,.
比较以上函数值可得,.
8.【解析】
.
若a≤0,则,x∈[0,1],函数单调递减.
∴当x=0时,有最大值,
若a>0,则令,解得.
∵x∈[0,1],则只考虑的情况.
当x变化时,,的变化情况如下表所示:
x
0
0
+
0
-
极大值
(1),即0<a<1,当时,有最大值.
(2),即a≥1,当x=1时,有最大值.
综上,当a≤0,x=0时,有最大值0;
当0<a<1,时,有最大值;
当a≥1,x=1时,有最大值3a―1.
