6.4.1平面几何中的向量方法-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 6.4.1平面几何中的向量方法-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 204.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 15:31:42 | ||
图片预览




文档简介
平面几何中的向量方法练习
一、单选题
在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足OP=OA+12(AB+AC),则|AP|等于(? ? ?)
A. 2 B. 1 C. 12 D. 4
已知四边形ABCD的对角线AC与BD相交于点O,且AO=OC,DO=OB,则四边形ABCD一定为??? (????)
A. 正方形 B. 梯形 C. 平行四边形 D. 菱形
如图,扇形的半径为1,圆心角∠BAC=150?,点P在弧BC上运动,AP=λAB+μAC,则3λ?μ的最小值是(? ?)
A. 0 B. 3 C. 2 D. ?1
如下图,在△ABC中,点D在线段BC上,且BD=3DC,若AD=λAB+μAC,则λμ=(??? )
A. 12
B. 13
C. 2
D. 23
在△ABC中,向量AB与AC满足(AB|AB|+AC|AC|)·BC=0,且BA|BA|·BCBC=22,则△ABC为(??? )
A. 等边三角形 B. 直角三角形
C. 等腰非等边三角形 D. 等腰直角三角形
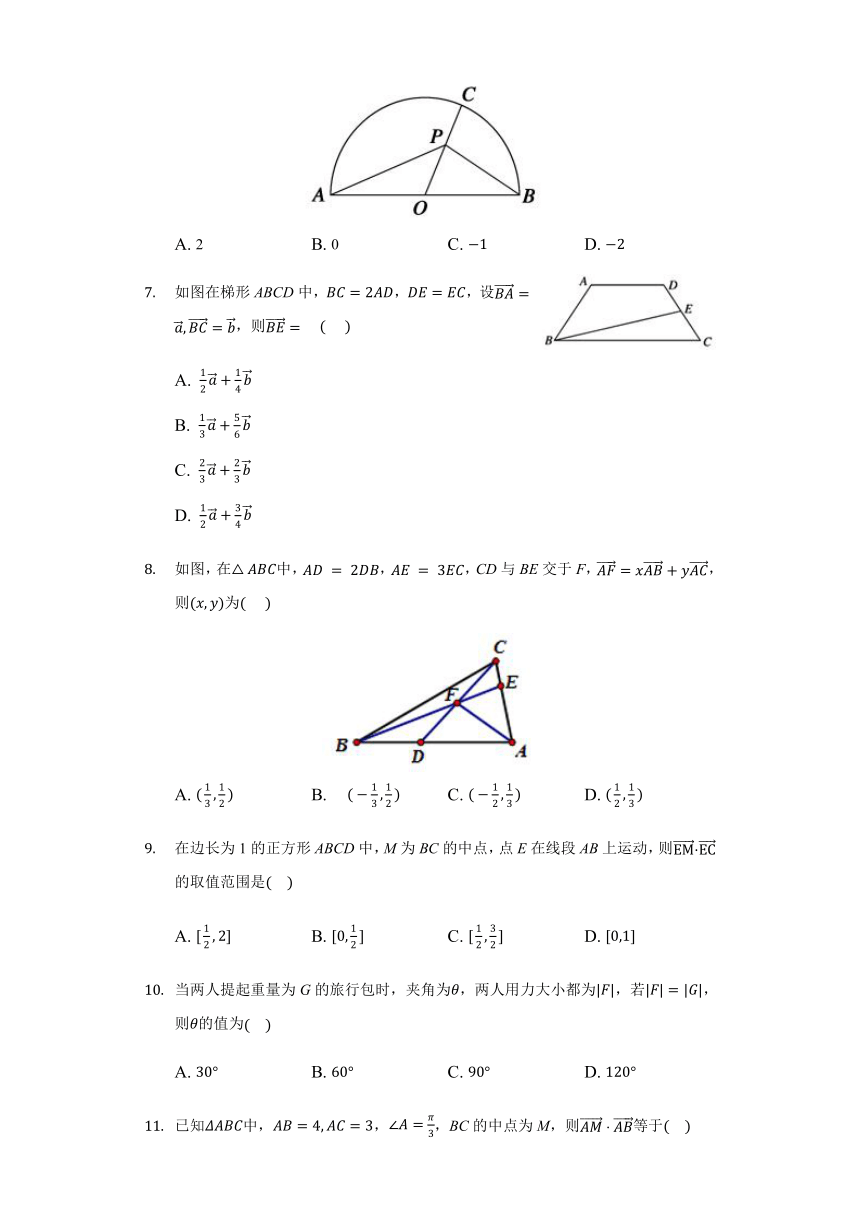
如图所示,半圆的直径AB=4,O为圆心,C是半圆上不同于A,B的任意一点,若P为半径OC上的动点,则PA+PB?PC的最小值是(????)
A. 2 B. 0 C. ?1 D. ?2
如图在梯形ABCD中,BC=2AD,DE=EC,设BA=a,BC=b,则BE=??? (??? )
A. 12a+14b
B. 13a+56b
C. 23a+23b
D. 12a+34b
如图,在△ABC中,AD?=?2DB,AE?=?3EC,CD与BE交于F,AF=xAB+yAC,则(x,y)为(??? )
A. (13,12) B. ? (?13,12) C. (?12,13) D. (12,13)
在边长为1的正方形ABCD中,M为BC的中点,点E在线段AB上运动,则EM·EC的取值范围是(? ?)
A. [12,2] B. [0,12] C. [12,32] D. [0,1]
当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若|F|=|G|,则θ的值为(????)
A. 30° B. 60° C. 90° D. 120°
已知ΔABC中,AB=4,AC=3,∠A=π3,BC的中点为M,则AM?AB等于(?? )
A. 152 B. 10 C. 11 D. 15
设O在△ABC的内部,且有OA+2OB+3OC=?0,则△ABC的面积和△AOC的面积之比为(? ? ? ? ?)
A. 3 B. 53 C. 2 D. 32
已知△ABC的外接圆的圆心为O,若AB+AC=2AO,且|OA|=|AC|=2,则向量BA在向量BC上的投影向量为(???????? ?)
A. 34BC B. 32BC C. 3BC D. 32BC
二、单空题
在四边形ABCD中,已知AB=(4,?2),AC=(7,4),AD=(3,6),则四边形ABCD的面积是________.
如图,在△ABC中,已知AB=10,AC=5,,点M是边AB的中点,点N在直线AC上,且AC=3AN,直线CM与BN相交于点P,则线段AP的长为??????????.
若点O是△ABC所在平面内的一点,且满足|OB?OC|=|OB+OC?2OA|,则△ABC的形状为________.
点M在△ABC内部,满足2MA+3MB+4MC=0,则S△MAC︰S△MAB=________.
在等腰梯形ABCD中,已知AB?//?DC,AB=2,BC=1,∠ABC=60°.点E和F分别在线段BC和DC上,且BE=23BC,DF=16DC,则AE·AF的值为________
在菱形ABCD中,∠DAB=60°,|AB|=1,则|BC+DC|=______.
三、解答题
如图平行四边形ABCD,点M是AB的中点,点N在BD上,且BN=13BD.求证:M,N,C三点共线.?????
如图,在平行四边形ABCD中,,垂足为P.
(1)若,求AP的长;
(2)设,,,,求的值.
在△ABC中,三边a,b,c的对角分别为A,B,C,已知a=3,.
(1)若c=23,求sinA;
(2)若AB边上的中线长为372,求△ABC的面积.
答案和解析
1.【答案】B
【解答】
解:由OP=OA+12(AB+AC)
可得OP?OA=12(AB+AC),
即AP=12(AB+AC),
可得点P是直角三角形斜边BC的中点,因为BC=2,
所以|AP|=1,
2.【答案】C
【解答】解:∵AB=AO+OB,DC=DO+OC,且AO=OC,DO=OB,
∴AB=DC,
∴AB//CD且AB=CD,
∴四边形ABCD一定为平行四边形.
3.【答案】D
【解答】
解:以AB为x轴,以A为原点,建立坐标系,如图,
设P(cosθ,sinθ),0°≤θ≤150°,
则A(0,0),B(1,0),C(?32,12),
∵AP=λAB+μAC,
∴(cosθ,sinθ)=λ(1,0)+μ(?32,12)
=(λ?32μ,μ2),
∴cosθ=λ?32μ,sinθ=μ2,
∴λ=cosθ+3sinθ,μ=2sinθ,
∴3λ?μ=3cosθ+3sinθ?2sinθ=3cosθ+sinθ=2sin(θ+60°),
∵0°≤θ≤150°,
∴60°≤θ+60°≤210°,
∴当θ=150°时,2sin(θ+60°)=?1,即3λ?μ的最小值为?1.
4.【答案】B
【解答】
解:?因为BD=3DC,
则AD=AB+BD=AB+34BC
=AB+34(AC?AB)
=14AB+34AC,
所以λ=14,μ=34,
则λμ=13.
5.【答案】D
【解答】
解:因为(ABAB+ACAC)·BC=0,
所以∠BAC的平分线与BC垂直,
所以三角形ABC是等腰三角形,且AB=AC.
又因为BABA·BCBC=22,
所以∠ABC=45°,
所以三角形ABC是等腰直角三角形.
6.【答案】D
【解答】
解:由平行四边形法则得PA+PB=2PO,
故(PA+PB)·PC=2PO·PC,又|PC|=2?|PO|
且PO·PC反向,设|PO|=t(0≤t≤2),
则(PA+PB)·PC=2PO·PC=?2t(2?t)
=2(t2?2t)=2[(t?1)2?1].
∵0≤t≤2,
∴当t=1时,(PA+PB)·PC的最小值为?2.
7.【答案】D
【解答】
解:取BC中点F,连接FA,
因为在梯形ABCD中,BC=2AD,所以四边形ADCF是平行四边形,
所以FA//CD,FA=CD,
则BE=BC+CE=BC+12CD=BC+12FA?
=BC+12(BA?BF)=BC+12(BA?12BC)?
=12BA+34BC=12a+34b.
8.【答案】A
【解答】
解:∵AD=2DB,AE=3EC,
设BF=λBE,CF=μCD,
∴AF=AB+BF=AB+λBE
=AB+λ(34AC?AB)=(1?λ)AB+34λAC,
且AF=AC+CF=AC+μCD
=AC+μ(23AB?AC)=23μAB+(1?μ)AC,
可得1?λ=23μ34λ=1?μ解得λ=23μ=12,
所以AF=13AB+12AC,
因为AF=xAB+yAC,
所以x=13,y=12,
则(x,y)为(13,12)?.
9.【答案】C
【解答】
解:(如图)以AB、AD分别为x、y轴建立坐标系,
进而可得C(1,1),M(1,12),设E(x,0)(0≤x≤1)
∴EC=(1?x,1),EM=(1?x,12),
∵0≤x≤1,
∴当x=1时,有最小值为12;
当x=0时,EM·EC有最大值为32,
由此可得的取值范围是[12,32]
10.【答案】D
【解答】
解:如图,|F|=|G|2cos?θ2.
又∵|F|=|G|,∴2cosθ2=1,∴θ=120?,
故选D.
11.【答案】C
【解答】
解:∵ΔABC中,AB=4,AC=3,∠A=π3,BC的中点为M,
∴AM?AB=12AB+AC?AB
=12AB?AB+12AC?AB
=8+3
=11,
12.【答案】A
【解答】
解:分别取AC、BC的中点D、E,
∵OA+2OB+3OC=0,
∴OA+OC=?2(?OB+OC),
即2OD=?4OE,
∴O是DE的一个三等分点,
∴S△AECS△AOC=DEDO=32,S△ABCS△AOC=31
13.【答案】A
【解答】
解:∵△ABC的外接圆的圆心为O,且AB+AC=2AO,∴O为BC的中点,即BC为外接圆的直径,∴∠BAC=90°.
∵|OA|=|AC|=2,
∴△AOC是边长为2的等边三角形,
∴∠ACB=60°,∠ABC=30°,
∴|BA|=BC?sin?60?=23,
∴向量BA在向量BC上的投影向量为.
14.【答案】30
【解答】
解:∵AB=(4,?2),AC=(7,4),AD=(3,6),
∴AB?AD=4×3?2×6=0,BC=AC?AB=(3,6)=AD,DC=AC?AD=(4,2)=AB,
∴AB⊥AD,BC//AD,AB//DC,
∴四边形ABCD为矩形,
∵|AB|=42+(?2)2=20,|AD|=32+62=45,
∴四边形ABCD的面积为20×45=30,
故答案为:30.
15.【答案】21
【解答】解:因为B,P,N三点共线,
所以存在实数x满足AP=xAB+(1?x)AN=xAB+1?x3AC,
因为C,P,M三点共线,
所以存在实数y满足AP=yAM+(1?y)AC=y2AB+(1?y)AC,
又AB,AC不共线,则x=y21?x3=1?y?x=25y=45,
所以AP=25AB+15AC,
所以AP2=125(4AB2+4AB·AC+AC2)
=125×(4×102+4×10×5×12+52)=21,
所以AP=21,
16.【答案】直角三角形
【解答】解:由|OB?OC|=|OB+OC?2OA|,得|CB|=|AB+AC|.
设D是BC的中点,则|CB|=2|AD|,即|AD|=12|CB|,
所以△ABC为直角三角形.
故答案为直角三角形.
17.【答案】3︰4
【解答】
解:如图,延长MA到E,使得ME=2MA,延长MB到F,使得MF=3MB,以ME、MF为临边作平行四边形MEDF,连接AD、EF,
由2MA+3MB+4MC=0,
即2MA+3MB=?4MC,
所以MD=?4MC,
∴M、C、D三点共线,且MD=4MC,
所以S△MAC=14·S△MAD=18S△MED=116S?MEDF,
S△MAB=16S△MEF=112S?MEDF,
所以S△MAC︰S△MAB=116:112=3:4,
故答案为3︰4.
18.【答案】2918
【解答】
解:以AB所在直线为x轴,A为原点建立如图所示的坐标系,
由于AB=2,BC=1,∠ABC=60°,所以CD=1,等腰梯形ABCD的高为32,
所以A(0,0),B(2,0),D12,32,C32,32,
所以BC=?12,32,DC=(1,0),
又因为BE=23BC,DF=16DC,
所以E53,33,F23,32,
因此AE·AF=53,33·23,32
=53×23+33×32=109+12=2918.
19.【答案】3
【解答】
解:如图,
|BC+DC|=AD+AB=|AC|,
在Rt△AOB中,AB=1,∠OAB=30°,
AC=2AO=2AB·cos?30°=3.
故答案为:3.
20.【答案】证明:由于M是AB的中点,且BN=13BD,
所以MN=MB+BN=12AB+13BD
=12AB+13BA+13AD=16AB+13AD,
MC=MB+BC=12AB+AD
=3(16AB+13AD)=3MN,
所以M,N,C三点共线.
21.【答案】解:,
解得.
,且B,P,O三点共线,
∴x+2y=1①,
又,,,
,
由可知,
展开化简得到,
联立①②解得,,故.
22.【答案】?解:(1)因为cosB+cosAcosCsinBcosC=3ab,
由正弦定理,得cosB+cosAcosCsinBcosC=3sinAsinB,
所以?cos(A+C)+cosAcosCsinBcosC=3sinAsinB.
所以sinAsinC=3sinAcosC.
又因为sinA≠0,
所以tanC=3.
因为C∈(0,π),
所以C=π3.
又因为asinA=csinC,
所以3sinA=2332,
所以sinA=34.
(2)设AB边上的中线为CD,则2CD=CA+CB,
所以4CD2=(CA+CB)2=b2+a2+2abcosC,
即37=b2+9+3b,b2+3b?28=0.
解得b=4或b=?7(舍去).
所以S△ABC=12absinC=12×4×3×32=33.
一、单选题
在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足OP=OA+12(AB+AC),则|AP|等于(? ? ?)
A. 2 B. 1 C. 12 D. 4
已知四边形ABCD的对角线AC与BD相交于点O,且AO=OC,DO=OB,则四边形ABCD一定为??? (????)
A. 正方形 B. 梯形 C. 平行四边形 D. 菱形
如图,扇形的半径为1,圆心角∠BAC=150?,点P在弧BC上运动,AP=λAB+μAC,则3λ?μ的最小值是(? ?)
A. 0 B. 3 C. 2 D. ?1
如下图,在△ABC中,点D在线段BC上,且BD=3DC,若AD=λAB+μAC,则λμ=(??? )
A. 12
B. 13
C. 2
D. 23
在△ABC中,向量AB与AC满足(AB|AB|+AC|AC|)·BC=0,且BA|BA|·BCBC=22,则△ABC为(??? )
A. 等边三角形 B. 直角三角形
C. 等腰非等边三角形 D. 等腰直角三角形
如图所示,半圆的直径AB=4,O为圆心,C是半圆上不同于A,B的任意一点,若P为半径OC上的动点,则PA+PB?PC的最小值是(????)
A. 2 B. 0 C. ?1 D. ?2
如图在梯形ABCD中,BC=2AD,DE=EC,设BA=a,BC=b,则BE=??? (??? )
A. 12a+14b
B. 13a+56b
C. 23a+23b
D. 12a+34b
如图,在△ABC中,AD?=?2DB,AE?=?3EC,CD与BE交于F,AF=xAB+yAC,则(x,y)为(??? )
A. (13,12) B. ? (?13,12) C. (?12,13) D. (12,13)
在边长为1的正方形ABCD中,M为BC的中点,点E在线段AB上运动,则EM·EC的取值范围是(? ?)
A. [12,2] B. [0,12] C. [12,32] D. [0,1]
当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若|F|=|G|,则θ的值为(????)
A. 30° B. 60° C. 90° D. 120°
已知ΔABC中,AB=4,AC=3,∠A=π3,BC的中点为M,则AM?AB等于(?? )
A. 152 B. 10 C. 11 D. 15
设O在△ABC的内部,且有OA+2OB+3OC=?0,则△ABC的面积和△AOC的面积之比为(? ? ? ? ?)
A. 3 B. 53 C. 2 D. 32
已知△ABC的外接圆的圆心为O,若AB+AC=2AO,且|OA|=|AC|=2,则向量BA在向量BC上的投影向量为(???????? ?)
A. 34BC B. 32BC C. 3BC D. 32BC
二、单空题
在四边形ABCD中,已知AB=(4,?2),AC=(7,4),AD=(3,6),则四边形ABCD的面积是________.
如图,在△ABC中,已知AB=10,AC=5,,点M是边AB的中点,点N在直线AC上,且AC=3AN,直线CM与BN相交于点P,则线段AP的长为??????????.
若点O是△ABC所在平面内的一点,且满足|OB?OC|=|OB+OC?2OA|,则△ABC的形状为________.
点M在△ABC内部,满足2MA+3MB+4MC=0,则S△MAC︰S△MAB=________.
在等腰梯形ABCD中,已知AB?//?DC,AB=2,BC=1,∠ABC=60°.点E和F分别在线段BC和DC上,且BE=23BC,DF=16DC,则AE·AF的值为________
在菱形ABCD中,∠DAB=60°,|AB|=1,则|BC+DC|=______.
三、解答题
如图平行四边形ABCD,点M是AB的中点,点N在BD上,且BN=13BD.求证:M,N,C三点共线.?????
如图,在平行四边形ABCD中,,垂足为P.
(1)若,求AP的长;
(2)设,,,,求的值.
在△ABC中,三边a,b,c的对角分别为A,B,C,已知a=3,.
(1)若c=23,求sinA;
(2)若AB边上的中线长为372,求△ABC的面积.
答案和解析
1.【答案】B
【解答】
解:由OP=OA+12(AB+AC)
可得OP?OA=12(AB+AC),
即AP=12(AB+AC),
可得点P是直角三角形斜边BC的中点,因为BC=2,
所以|AP|=1,
2.【答案】C
【解答】解:∵AB=AO+OB,DC=DO+OC,且AO=OC,DO=OB,
∴AB=DC,
∴AB//CD且AB=CD,
∴四边形ABCD一定为平行四边形.
3.【答案】D
【解答】
解:以AB为x轴,以A为原点,建立坐标系,如图,
设P(cosθ,sinθ),0°≤θ≤150°,
则A(0,0),B(1,0),C(?32,12),
∵AP=λAB+μAC,
∴(cosθ,sinθ)=λ(1,0)+μ(?32,12)
=(λ?32μ,μ2),
∴cosθ=λ?32μ,sinθ=μ2,
∴λ=cosθ+3sinθ,μ=2sinθ,
∴3λ?μ=3cosθ+3sinθ?2sinθ=3cosθ+sinθ=2sin(θ+60°),
∵0°≤θ≤150°,
∴60°≤θ+60°≤210°,
∴当θ=150°时,2sin(θ+60°)=?1,即3λ?μ的最小值为?1.
4.【答案】B
【解答】
解:?因为BD=3DC,
则AD=AB+BD=AB+34BC
=AB+34(AC?AB)
=14AB+34AC,
所以λ=14,μ=34,
则λμ=13.
5.【答案】D
【解答】
解:因为(ABAB+ACAC)·BC=0,
所以∠BAC的平分线与BC垂直,
所以三角形ABC是等腰三角形,且AB=AC.
又因为BABA·BCBC=22,
所以∠ABC=45°,
所以三角形ABC是等腰直角三角形.
6.【答案】D
【解答】
解:由平行四边形法则得PA+PB=2PO,
故(PA+PB)·PC=2PO·PC,又|PC|=2?|PO|
且PO·PC反向,设|PO|=t(0≤t≤2),
则(PA+PB)·PC=2PO·PC=?2t(2?t)
=2(t2?2t)=2[(t?1)2?1].
∵0≤t≤2,
∴当t=1时,(PA+PB)·PC的最小值为?2.
7.【答案】D
【解答】
解:取BC中点F,连接FA,
因为在梯形ABCD中,BC=2AD,所以四边形ADCF是平行四边形,
所以FA//CD,FA=CD,
则BE=BC+CE=BC+12CD=BC+12FA?
=BC+12(BA?BF)=BC+12(BA?12BC)?
=12BA+34BC=12a+34b.
8.【答案】A
【解答】
解:∵AD=2DB,AE=3EC,
设BF=λBE,CF=μCD,
∴AF=AB+BF=AB+λBE
=AB+λ(34AC?AB)=(1?λ)AB+34λAC,
且AF=AC+CF=AC+μCD
=AC+μ(23AB?AC)=23μAB+(1?μ)AC,
可得1?λ=23μ34λ=1?μ解得λ=23μ=12,
所以AF=13AB+12AC,
因为AF=xAB+yAC,
所以x=13,y=12,
则(x,y)为(13,12)?.
9.【答案】C
【解答】
解:(如图)以AB、AD分别为x、y轴建立坐标系,
进而可得C(1,1),M(1,12),设E(x,0)(0≤x≤1)
∴EC=(1?x,1),EM=(1?x,12),
∵0≤x≤1,
∴当x=1时,有最小值为12;
当x=0时,EM·EC有最大值为32,
由此可得的取值范围是[12,32]
10.【答案】D
【解答】
解:如图,|F|=|G|2cos?θ2.
又∵|F|=|G|,∴2cosθ2=1,∴θ=120?,
故选D.
11.【答案】C
【解答】
解:∵ΔABC中,AB=4,AC=3,∠A=π3,BC的中点为M,
∴AM?AB=12AB+AC?AB
=12AB?AB+12AC?AB
=8+3
=11,
12.【答案】A
【解答】
解:分别取AC、BC的中点D、E,
∵OA+2OB+3OC=0,
∴OA+OC=?2(?OB+OC),
即2OD=?4OE,
∴O是DE的一个三等分点,
∴S△AECS△AOC=DEDO=32,S△ABCS△AOC=31
13.【答案】A
【解答】
解:∵△ABC的外接圆的圆心为O,且AB+AC=2AO,∴O为BC的中点,即BC为外接圆的直径,∴∠BAC=90°.
∵|OA|=|AC|=2,
∴△AOC是边长为2的等边三角形,
∴∠ACB=60°,∠ABC=30°,
∴|BA|=BC?sin?60?=23,
∴向量BA在向量BC上的投影向量为.
14.【答案】30
【解答】
解:∵AB=(4,?2),AC=(7,4),AD=(3,6),
∴AB?AD=4×3?2×6=0,BC=AC?AB=(3,6)=AD,DC=AC?AD=(4,2)=AB,
∴AB⊥AD,BC//AD,AB//DC,
∴四边形ABCD为矩形,
∵|AB|=42+(?2)2=20,|AD|=32+62=45,
∴四边形ABCD的面积为20×45=30,
故答案为:30.
15.【答案】21
【解答】解:因为B,P,N三点共线,
所以存在实数x满足AP=xAB+(1?x)AN=xAB+1?x3AC,
因为C,P,M三点共线,
所以存在实数y满足AP=yAM+(1?y)AC=y2AB+(1?y)AC,
又AB,AC不共线,则x=y21?x3=1?y?x=25y=45,
所以AP=25AB+15AC,
所以AP2=125(4AB2+4AB·AC+AC2)
=125×(4×102+4×10×5×12+52)=21,
所以AP=21,
16.【答案】直角三角形
【解答】解:由|OB?OC|=|OB+OC?2OA|,得|CB|=|AB+AC|.
设D是BC的中点,则|CB|=2|AD|,即|AD|=12|CB|,
所以△ABC为直角三角形.
故答案为直角三角形.
17.【答案】3︰4
【解答】
解:如图,延长MA到E,使得ME=2MA,延长MB到F,使得MF=3MB,以ME、MF为临边作平行四边形MEDF,连接AD、EF,
由2MA+3MB+4MC=0,
即2MA+3MB=?4MC,
所以MD=?4MC,
∴M、C、D三点共线,且MD=4MC,
所以S△MAC=14·S△MAD=18S△MED=116S?MEDF,
S△MAB=16S△MEF=112S?MEDF,
所以S△MAC︰S△MAB=116:112=3:4,
故答案为3︰4.
18.【答案】2918
【解答】
解:以AB所在直线为x轴,A为原点建立如图所示的坐标系,
由于AB=2,BC=1,∠ABC=60°,所以CD=1,等腰梯形ABCD的高为32,
所以A(0,0),B(2,0),D12,32,C32,32,
所以BC=?12,32,DC=(1,0),
又因为BE=23BC,DF=16DC,
所以E53,33,F23,32,
因此AE·AF=53,33·23,32
=53×23+33×32=109+12=2918.
19.【答案】3
【解答】
解:如图,
|BC+DC|=AD+AB=|AC|,
在Rt△AOB中,AB=1,∠OAB=30°,
AC=2AO=2AB·cos?30°=3.
故答案为:3.
20.【答案】证明:由于M是AB的中点,且BN=13BD,
所以MN=MB+BN=12AB+13BD
=12AB+13BA+13AD=16AB+13AD,
MC=MB+BC=12AB+AD
=3(16AB+13AD)=3MN,
所以M,N,C三点共线.
21.【答案】解:,
解得.
,且B,P,O三点共线,
∴x+2y=1①,
又,,,
,
由可知,
展开化简得到,
联立①②解得,,故.
22.【答案】?解:(1)因为cosB+cosAcosCsinBcosC=3ab,
由正弦定理,得cosB+cosAcosCsinBcosC=3sinAsinB,
所以?cos(A+C)+cosAcosCsinBcosC=3sinAsinB.
所以sinAsinC=3sinAcosC.
又因为sinA≠0,
所以tanC=3.
因为C∈(0,π),
所以C=π3.
又因为asinA=csinC,
所以3sinA=2332,
所以sinA=34.
(2)设AB边上的中线为CD,则2CD=CA+CB,
所以4CD2=(CA+CB)2=b2+a2+2abcosC,
即37=b2+9+3b,b2+3b?28=0.
解得b=4或b=?7(舍去).
所以S△ABC=12absinC=12×4×3×32=33.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
