8.3.1 棱柱、棱锥、棱台的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 00:00:00 | ||
图片预览




文档简介
棱柱、棱锥、棱台的表面积和体积练习
一、单选题
若正方体八个顶点中有四个恰好是正四面体的顶点,则正方体的表面积与正四面体的表面积之比是(? ? ? ?)
A. 3 B. 2 C. 23 D. 32
正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,则棱台的侧面积为(????)
A. 4cm2 B. 8cm2 C. 43cm2 D. 83cm2
三棱台ABC—A1B1C1中,A1B1:AB=1:2,则三棱锥A1—ABC,A1—B1C1B,A1—C1BC的体积之比为(? ? ? )
A. 1:1:1 B. 2:1:1 C. 4:2:1 D. 4:1:2
将一个正方体截去四个角后得到一个正四面体,这个正四面体的体积是正方体体积的(? ? )
A. 12 B. 13 C. 16 D. 14
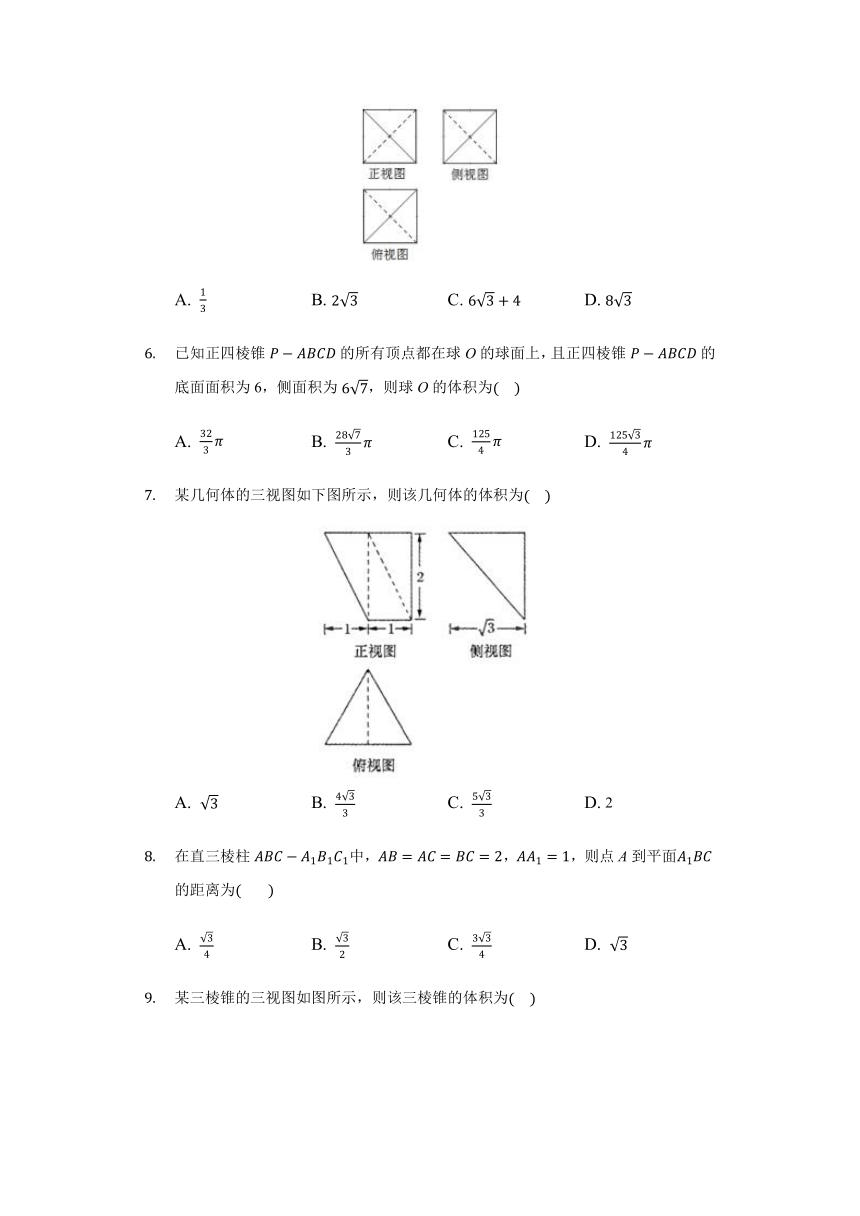
已知某空间几何体的三视图如图所示,每个小方格是边长为1的正方形,则该几何体的表面积为(????)
A. 13 B. 23 C. 63+4 D. 83
已知正四棱锥P?ABCD的所有顶点都在球O的球面上,且正四棱锥P?ABCD的底面面积为6,侧面积为67,则球O的体积为(????)
A. 323π B. 2873π C. 1254π D. 12534π
某几何体的三视图如下图所示,则该几何体的体积为(????)
A. 3 B. 433 C. 533 D. 2
在直三棱柱ABC?A1B1C1中,AB=AC=BC=2,AA1=1,则点A到平面A1BC的距离为(???? ?)
A. 34 B. 32 C. 334 D. 3
某三棱锥的三视图如图所示,则该三棱锥的体积为(????)
A. 60 B. 30 C. 20 D. 10
已知三棱锥P?ABC的四个顶点均在同一个确定的球面上,且BA=BC=6,∠ABC=π2,若三棱锥P?ABC体积的最大值为3,则其外接球的半径为(??? )
A. 2 B. 3 C. 4 D. 5
如图,在四棱锥P?ABCD中,PA=PB=PC=PD=2,底面ABCD是边长为2的正方形.点E是PC的中点,过点A,E作棱锥的截面,分别与侧棱PB,PD交于M,N两点,则四棱锥P?AMEN体积的最小值为(????)
A. 223 B. 233 C. 229 D. 239
二、单空题
已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
如图,在棱长为a的正方体ABCD?A1B1C1D1中,则点A到平面A1BD的距离d=________.
正六棱柱底面边长为10,高为15,则这个正六棱柱的体积是??????????.
已知正方体ABCD?A1B1C1D1的棱长为2,E,F,G,H分别是AB,BC,CD,DA的中点,则四棱锥A1?EFGH的体积为??????????.
在《九章算术》中,堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC?A1B1C1中,AC⊥BC,AA1=AB=2,则当阳马B?A1ACC1的体积最大时,堑堵ABC?A1B1C1的体积为??????????.
三、解答题
已知正三棱台的上、下底面边长分别为3cm和6cm,高为32cm,求此正三棱台的表面积.
如图,在正三棱柱ABC?A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
(Ⅰ)证明:平面AEF⊥平面ACC1A1;
(Ⅱ)若AB=EC=2,求三棱锥C?AEF的体积.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
(1)求证:PA?//平面BDE;
(2)求证:BD⊥平面PAC;
(3)若AB=2,PB=6,求三棱锥B?CDE的体积.
答案和解析
1.【答案】A
【解答】
解:设正方体的棱长为a,则正方体的表面积是6a2,
以正方体的顶点为顶点作正四面体,棱长为2a,
它的表面积是4×34×(2a)2=23a2,
则正方体的表面积与正四面体的表面积之比为3.
2.【答案】D
【解答】
解:正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,
所以棱台的斜高为:22?(3?12)2=3cm.
所以棱台的侧面积是:4×1+32×3=83cm2.
3.【答案】D
【解答】
解:设点A1到底面ABC的距离为h,
则三棱锥A1?ABC的体积V1=13×?×S△ABC,
三棱锥A1?B1C1B的体积V2=13×?×S△A1B1C1=13×?×14×S△ABC=14V1,
三棱锥A1?C1BC的体积V3=2V2=12V1,
所以三棱锥A1?ABC,A1?B1C1B,A1?C1BC的体积之比为4:1:2.
4.【答案】B
【解答】
解:将正方体ABCD?A′B′C′D′截去四个角后得到一个四面体BDA′C′,
设正方体边长为a,
则VB?B′A′C′=VA′?ABD=VD?A′C′D′=VC′?BCD=13×12×a×a×a=a36.
∴四面体BDA1C1的体积:
V=V正方体?4VB?B′A′C′=a3?2a33=a33.
∴这个四面体的体积是原正方体体积的13.
5.【答案】D
【解答】
解:根据三视图知该几何体是棱长为2的正方体去掉四个全等的三棱锥所余下的几何体,如图所示:
则该几何体是棱长为22的正四面体,
所以该正四面体的表面积为
S正四面体=4S正△ABC=4×12×(22)2×sin60°=83.
6.【答案】A
【解答】
解:设底面边长为a,侧棱长为b,
由底面面积为6得;a2=6,得a=6,
∵侧面积为67,
∴4×12×b2?622×6=67,得b=23,
连接AC,BD交于点O1,连接PO1,则易知PO1⊥平面ABCD,
故四棱锥P?ABCD的高PO1=12?3=3,且点O在直线PO1上,
连接OA,设球的半径为R,
∴R2=(3?R)2+(3)2,
∴R=2,
∴球O的体积为4π3?R3=32π3,
?7.【答案】A
【解答】
解:由已知中的三视图可得:该几何体是一个以正视图为底面的四棱锥,?
其底面面积S=12×(1+2)×2=3,高?=3,?
故体积V=13S?=13×3×3=3,?
8.【答案】B
【解答】
解:?设点A到平面A1BC的距离为h,
因AB=AC=BC=2,AA1=1,
则A1C=A1B=5,
取BC中点D,则AD=3,且AD⊥BC,A1D⊥BC,
故A1D=A1C2?CD2=2,
∴S△A1BC=12BC·A1D=12×2×2=2,
而S△ABC=12×2×3=3,
∵VA1?ABC=VA?A1BC,
∴13S△ABC·AA1=13S△A1BC·?,
∴13×3×1=13×2×?,
解得?=32.
9.【答案】D
【解答】
解:
由三视图可知:该几何体为三棱锥P?ABC,
该三棱锥的体积V=13×12×5×3×4=10.
10.【答案】A
【解答】
解:∵△ABC是等腰直角三角形,
∴AC为截面圆的直径,故外接球的球心O在截面ABC中的射影为AC的中点D,
∴当P,O,D共线且P,O位于截面同一侧时棱锥的体积最大,
棱锥的最大高度为PD,
∴13×12×6×6×PD=3,解得PD=3,
设外接球的半径为R,则OD=3?R,OC=R,
在△ODC中,CD=12AC=3,
由勾股定理得:(3?R)2+3=R2,解得R=2.
11.【答案】D
【解析】解:∵在四棱锥P?ABCD中,PA=PB=PC=PD=2,底面ABCD是边长为2的正方形.
点E是PC的中点,过点A,E作棱锥的截面,分别与侧棱PB,PD交于M,N两点,
∴VP?AMEN=VA?MNP+VE?MNP=13S△PMN?32=12S△PMN,
依题意当S△PMN最小时,四棱锥P?AMEN体积取最小值,
M,O,V三点共线,且PN=λPD,PM=μPB,
|PD||PN|=1λ,|PB||PM|=1μ,
PV=23PO=13(PD+PB)=13λPN+13μPM,
13λ+13μ=1,∴2|PN|+2|PM|=3,
∵3=2|PN|+2|PM|≥22|PN|?2|PM|,
∴|PN|?|PM|≥169,当且仅当2|PN|=2|PM|时,取“=”,
∴VP?AMNE=12S△PMN=12×12×|PN|×|PM|×sinπ3≥12×12×169×32=293.
∴四棱锥P?AMEN体积的最小值为239.
12.【答案】90;138
【解答】
解:该几何体的体积V=4×6×3+12×4×3×3=90,
表面积S=2(4×6+4×3+6×3)?3×3+12×4×3×2+32+42×3+3×4=138.
故答案为:90;138
13.【答案】33a
【解答】
解:在三棱锥A1?ABD中,AA1是三棱锥A1?ABD的高,
AB=AD=AA1=a,A1B=BD=A1D=2a,
∵V三棱锥A1?ABD=V三棱锥A?A1BD,
∴13×12a2×a=13×12×2a×32×2a×d,
∴d=33a,
∴点A到平面A1BD的距离为33a.
故答案为33a.
14.【答案】22503
【解答】
解:∵正六棱柱底面边长为10,
∴正六棱柱的底面积为S=6×12×10×10×sin60°=300×32=1503,
又正六棱柱的高为15,
∴这个正六棱柱的体积是1503×15=22503.
故答案为:22503.
15.【答案】43
【解答】
解:
∵正方体ABCD?A1B1C1D1的棱长为2,
E,F,G,H分别是四条棱AB,BC,CD,DA上的中点,
∴四边形EFGH是边长为2的正方形,
点A1到平面EFGH的距离d=AA1=2,
∴四棱锥A1?EFGH体积为:
VA1?EFGH=13×d×S正方形EFGH
=13×2×2×2
=43.
16.【答案】2
【解答】
解:设AC=m,则BC=4?m2,
VB?A1ACC1=13×2m×4?m2=23m4?m2,
∴当m4?m2最大时,?VB?A1ACC1体积最大,
m4?m2=m2(4?m2)≤m2+(4?m2)2=2,
当且仅当m=2时,取最大值,
∴当“阳马”即四棱锥B?A1ACC1体积最大时,AC=BC=2,
所以堑堵ABC?A1B1C1的体积为12×2×2×2=2.
17.【答案】解:如图所示,画出正三棱台ABC?A1B1C1,OO1为正三棱台的高,
DD1为侧面梯形BCC1B1的高,则四边形ODD1O1为直角梯形,
所以DD1=OO12+(OD?O1D1)2=(32)2+(3?32)2=3.
所以此正三棱台的表面积S表=S侧+S底=3×12×(3+6)×3+34×32+34×62=9943cm2.
18.【答案】(1)证明:取AC中点M,连接BM,
因为正三棱柱ABC?A1B1C1中,BC=AB,
所以BM⊥AC,
因为正三棱柱ABC?A1B1C1中平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,BM?平面ABC,
所以BM⊥平面ACC1A1.
取AE中点N,连接MN,FN,则MN//EC,且MN=12EC,
又因为BB1//CC1,EC=2FB,所以FB//EC且FB=12EC,
所以MN//FB且MN=FB,
所以四边形BMNF是平行四边形,
所以FN//BM,
所以FN⊥平面ACC1A1.
又FN?平面AEF,
所以平面AEF⊥平面ACC1A1.
(2)解:作AD⊥BC于D,垂足为D,
因为正三棱柱ABC?A1B1C1中AB=AC=2,
所以AD⊥BC,且AD=3,
又因为正三棱柱ABC?A1B1C1中,平面BB1C1C⊥平面ABC,平面BB1C1C∩平面ABC=AC,AD?平面ABC,
所以AD⊥平面BB1C1C,
所以VA?CEF=13×S△CEF×AD
=13×12×2×2×3=233.
故VC?AEF=VA?CEF=233.
19.【答案】(1)证明:连接AC,OE,
四边形ABCD为正方形,则O为AC中点,
在△PAC中,E、O分别为PC、AC中点,
∴?EO?//PA,
又PA?平面BED,EO?平面BED,
∴PA?//平面BED;
(2)证明:∵PO⊥平面ABCD,
BD?平面ABCD,∴PO⊥BD,
又四边形ABCD为正方形,
∴BD⊥AC,
又PO?平面PAC,AC?平面PAC,
PO∩AC=O,
∴BD⊥平面PAC;
(3)解:由题意知:OB=2,又PB=6,
∴PO=PB2?OB2=2,
S△BCD=12BC·CD=12×2×2=2,
点E到面BCD的距离为?=12PO=1,
∴VB?CDE=VE?BCD
=13S△BCD·?=13×2×1=23.
一、单选题
若正方体八个顶点中有四个恰好是正四面体的顶点,则正方体的表面积与正四面体的表面积之比是(? ? ? ?)
A. 3 B. 2 C. 23 D. 32
正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,则棱台的侧面积为(????)
A. 4cm2 B. 8cm2 C. 43cm2 D. 83cm2
三棱台ABC—A1B1C1中,A1B1:AB=1:2,则三棱锥A1—ABC,A1—B1C1B,A1—C1BC的体积之比为(? ? ? )
A. 1:1:1 B. 2:1:1 C. 4:2:1 D. 4:1:2
将一个正方体截去四个角后得到一个正四面体,这个正四面体的体积是正方体体积的(? ? )
A. 12 B. 13 C. 16 D. 14
已知某空间几何体的三视图如图所示,每个小方格是边长为1的正方形,则该几何体的表面积为(????)
A. 13 B. 23 C. 63+4 D. 83
已知正四棱锥P?ABCD的所有顶点都在球O的球面上,且正四棱锥P?ABCD的底面面积为6,侧面积为67,则球O的体积为(????)
A. 323π B. 2873π C. 1254π D. 12534π
某几何体的三视图如下图所示,则该几何体的体积为(????)
A. 3 B. 433 C. 533 D. 2
在直三棱柱ABC?A1B1C1中,AB=AC=BC=2,AA1=1,则点A到平面A1BC的距离为(???? ?)
A. 34 B. 32 C. 334 D. 3
某三棱锥的三视图如图所示,则该三棱锥的体积为(????)
A. 60 B. 30 C. 20 D. 10
已知三棱锥P?ABC的四个顶点均在同一个确定的球面上,且BA=BC=6,∠ABC=π2,若三棱锥P?ABC体积的最大值为3,则其外接球的半径为(??? )
A. 2 B. 3 C. 4 D. 5
如图,在四棱锥P?ABCD中,PA=PB=PC=PD=2,底面ABCD是边长为2的正方形.点E是PC的中点,过点A,E作棱锥的截面,分别与侧棱PB,PD交于M,N两点,则四棱锥P?AMEN体积的最小值为(????)
A. 223 B. 233 C. 229 D. 239
二、单空题
已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
如图,在棱长为a的正方体ABCD?A1B1C1D1中,则点A到平面A1BD的距离d=________.
正六棱柱底面边长为10,高为15,则这个正六棱柱的体积是??????????.
已知正方体ABCD?A1B1C1D1的棱长为2,E,F,G,H分别是AB,BC,CD,DA的中点,则四棱锥A1?EFGH的体积为??????????.
在《九章算术》中,堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC?A1B1C1中,AC⊥BC,AA1=AB=2,则当阳马B?A1ACC1的体积最大时,堑堵ABC?A1B1C1的体积为??????????.
三、解答题
已知正三棱台的上、下底面边长分别为3cm和6cm,高为32cm,求此正三棱台的表面积.
如图,在正三棱柱ABC?A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
(Ⅰ)证明:平面AEF⊥平面ACC1A1;
(Ⅱ)若AB=EC=2,求三棱锥C?AEF的体积.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
(1)求证:PA?//平面BDE;
(2)求证:BD⊥平面PAC;
(3)若AB=2,PB=6,求三棱锥B?CDE的体积.
答案和解析
1.【答案】A
【解答】
解:设正方体的棱长为a,则正方体的表面积是6a2,
以正方体的顶点为顶点作正四面体,棱长为2a,
它的表面积是4×34×(2a)2=23a2,
则正方体的表面积与正四面体的表面积之比为3.
2.【答案】D
【解答】
解:正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,
所以棱台的斜高为:22?(3?12)2=3cm.
所以棱台的侧面积是:4×1+32×3=83cm2.
3.【答案】D
【解答】
解:设点A1到底面ABC的距离为h,
则三棱锥A1?ABC的体积V1=13×?×S△ABC,
三棱锥A1?B1C1B的体积V2=13×?×S△A1B1C1=13×?×14×S△ABC=14V1,
三棱锥A1?C1BC的体积V3=2V2=12V1,
所以三棱锥A1?ABC,A1?B1C1B,A1?C1BC的体积之比为4:1:2.
4.【答案】B
【解答】
解:将正方体ABCD?A′B′C′D′截去四个角后得到一个四面体BDA′C′,
设正方体边长为a,
则VB?B′A′C′=VA′?ABD=VD?A′C′D′=VC′?BCD=13×12×a×a×a=a36.
∴四面体BDA1C1的体积:
V=V正方体?4VB?B′A′C′=a3?2a33=a33.
∴这个四面体的体积是原正方体体积的13.
5.【答案】D
【解答】
解:根据三视图知该几何体是棱长为2的正方体去掉四个全等的三棱锥所余下的几何体,如图所示:
则该几何体是棱长为22的正四面体,
所以该正四面体的表面积为
S正四面体=4S正△ABC=4×12×(22)2×sin60°=83.
6.【答案】A
【解答】
解:设底面边长为a,侧棱长为b,
由底面面积为6得;a2=6,得a=6,
∵侧面积为67,
∴4×12×b2?622×6=67,得b=23,
连接AC,BD交于点O1,连接PO1,则易知PO1⊥平面ABCD,
故四棱锥P?ABCD的高PO1=12?3=3,且点O在直线PO1上,
连接OA,设球的半径为R,
∴R2=(3?R)2+(3)2,
∴R=2,
∴球O的体积为4π3?R3=32π3,
?7.【答案】A
【解答】
解:由已知中的三视图可得:该几何体是一个以正视图为底面的四棱锥,?
其底面面积S=12×(1+2)×2=3,高?=3,?
故体积V=13S?=13×3×3=3,?
8.【答案】B
【解答】
解:?设点A到平面A1BC的距离为h,
因AB=AC=BC=2,AA1=1,
则A1C=A1B=5,
取BC中点D,则AD=3,且AD⊥BC,A1D⊥BC,
故A1D=A1C2?CD2=2,
∴S△A1BC=12BC·A1D=12×2×2=2,
而S△ABC=12×2×3=3,
∵VA1?ABC=VA?A1BC,
∴13S△ABC·AA1=13S△A1BC·?,
∴13×3×1=13×2×?,
解得?=32.
9.【答案】D
【解答】
解:
由三视图可知:该几何体为三棱锥P?ABC,
该三棱锥的体积V=13×12×5×3×4=10.
10.【答案】A
【解答】
解:∵△ABC是等腰直角三角形,
∴AC为截面圆的直径,故外接球的球心O在截面ABC中的射影为AC的中点D,
∴当P,O,D共线且P,O位于截面同一侧时棱锥的体积最大,
棱锥的最大高度为PD,
∴13×12×6×6×PD=3,解得PD=3,
设外接球的半径为R,则OD=3?R,OC=R,
在△ODC中,CD=12AC=3,
由勾股定理得:(3?R)2+3=R2,解得R=2.
11.【答案】D
【解析】解:∵在四棱锥P?ABCD中,PA=PB=PC=PD=2,底面ABCD是边长为2的正方形.
点E是PC的中点,过点A,E作棱锥的截面,分别与侧棱PB,PD交于M,N两点,
∴VP?AMEN=VA?MNP+VE?MNP=13S△PMN?32=12S△PMN,
依题意当S△PMN最小时,四棱锥P?AMEN体积取最小值,
M,O,V三点共线,且PN=λPD,PM=μPB,
|PD||PN|=1λ,|PB||PM|=1μ,
PV=23PO=13(PD+PB)=13λPN+13μPM,
13λ+13μ=1,∴2|PN|+2|PM|=3,
∵3=2|PN|+2|PM|≥22|PN|?2|PM|,
∴|PN|?|PM|≥169,当且仅当2|PN|=2|PM|时,取“=”,
∴VP?AMNE=12S△PMN=12×12×|PN|×|PM|×sinπ3≥12×12×169×32=293.
∴四棱锥P?AMEN体积的最小值为239.
12.【答案】90;138
【解答】
解:该几何体的体积V=4×6×3+12×4×3×3=90,
表面积S=2(4×6+4×3+6×3)?3×3+12×4×3×2+32+42×3+3×4=138.
故答案为:90;138
13.【答案】33a
【解答】
解:在三棱锥A1?ABD中,AA1是三棱锥A1?ABD的高,
AB=AD=AA1=a,A1B=BD=A1D=2a,
∵V三棱锥A1?ABD=V三棱锥A?A1BD,
∴13×12a2×a=13×12×2a×32×2a×d,
∴d=33a,
∴点A到平面A1BD的距离为33a.
故答案为33a.
14.【答案】22503
【解答】
解:∵正六棱柱底面边长为10,
∴正六棱柱的底面积为S=6×12×10×10×sin60°=300×32=1503,
又正六棱柱的高为15,
∴这个正六棱柱的体积是1503×15=22503.
故答案为:22503.
15.【答案】43
【解答】
解:
∵正方体ABCD?A1B1C1D1的棱长为2,
E,F,G,H分别是四条棱AB,BC,CD,DA上的中点,
∴四边形EFGH是边长为2的正方形,
点A1到平面EFGH的距离d=AA1=2,
∴四棱锥A1?EFGH体积为:
VA1?EFGH=13×d×S正方形EFGH
=13×2×2×2
=43.
16.【答案】2
【解答】
解:设AC=m,则BC=4?m2,
VB?A1ACC1=13×2m×4?m2=23m4?m2,
∴当m4?m2最大时,?VB?A1ACC1体积最大,
m4?m2=m2(4?m2)≤m2+(4?m2)2=2,
当且仅当m=2时,取最大值,
∴当“阳马”即四棱锥B?A1ACC1体积最大时,AC=BC=2,
所以堑堵ABC?A1B1C1的体积为12×2×2×2=2.
17.【答案】解:如图所示,画出正三棱台ABC?A1B1C1,OO1为正三棱台的高,
DD1为侧面梯形BCC1B1的高,则四边形ODD1O1为直角梯形,
所以DD1=OO12+(OD?O1D1)2=(32)2+(3?32)2=3.
所以此正三棱台的表面积S表=S侧+S底=3×12×(3+6)×3+34×32+34×62=9943cm2.
18.【答案】(1)证明:取AC中点M,连接BM,
因为正三棱柱ABC?A1B1C1中,BC=AB,
所以BM⊥AC,
因为正三棱柱ABC?A1B1C1中平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,BM?平面ABC,
所以BM⊥平面ACC1A1.
取AE中点N,连接MN,FN,则MN//EC,且MN=12EC,
又因为BB1//CC1,EC=2FB,所以FB//EC且FB=12EC,
所以MN//FB且MN=FB,
所以四边形BMNF是平行四边形,
所以FN//BM,
所以FN⊥平面ACC1A1.
又FN?平面AEF,
所以平面AEF⊥平面ACC1A1.
(2)解:作AD⊥BC于D,垂足为D,
因为正三棱柱ABC?A1B1C1中AB=AC=2,
所以AD⊥BC,且AD=3,
又因为正三棱柱ABC?A1B1C1中,平面BB1C1C⊥平面ABC,平面BB1C1C∩平面ABC=AC,AD?平面ABC,
所以AD⊥平面BB1C1C,
所以VA?CEF=13×S△CEF×AD
=13×12×2×2×3=233.
故VC?AEF=VA?CEF=233.
19.【答案】(1)证明:连接AC,OE,
四边形ABCD为正方形,则O为AC中点,
在△PAC中,E、O分别为PC、AC中点,
∴?EO?//PA,
又PA?平面BED,EO?平面BED,
∴PA?//平面BED;
(2)证明:∵PO⊥平面ABCD,
BD?平面ABCD,∴PO⊥BD,
又四边形ABCD为正方形,
∴BD⊥AC,
又PO?平面PAC,AC?平面PAC,
PO∩AC=O,
∴BD⊥平面PAC;
(3)解:由题意知:OB=2,又PB=6,
∴PO=PB2?OB2=2,
S△BCD=12BC·CD=12×2×2=2,
点E到面BCD的距离为?=12PO=1,
∴VB?CDE=VE?BCD
=13S△BCD·?=13×2×1=23.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
