5.3导数在研究函数中的应用-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第二册专题训练(Word含答案)
文档属性
| 名称 | 5.3导数在研究函数中的应用-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第二册专题训练(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 54.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 15:49:50 | ||
图片预览



文档简介
高一数学人教版(2019)选择性必修第二册
【5.3导数在研究函数中的应用专题训练】
【基础巩固】
1.已知函数 f(x)={ex?1?1,x≥1,lnx,0①存在 a,b∈R ,函数 g(x) 没有零点;②存在 a,b∈R ,函数 g(x) 恰有三个零点;③任意 b∈R ,存在 a>0 ,函数 g(x) 恰有一个零点;④任意 a>0 ,存在 b∈R ,函数 g(x) 恰有二个零点;
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.已知函数 f(x)=x3?12x,x∈[?3,3] ,则 f(x) 的最大值为(??? )
A.?-9?????????????????????????????????????????B.?-16?????????????????????????????????????????C.?16?????????????????????????????????????????D.?9
3.已知 f(x)=lnx+ax(a≠0) ,则( ??)
A.?当 a<0 时, f(x) 存在极小值 f(a)???????????????????B.?当 a<0 时, f(x) 存在极大值 f(a)
C.?当 a>0 时, f(x) 存在极小值 f(a)???????????????????D.?当 a>0 时, f(x) 存在极大值 f(a)
4.若函数 f(x)=?x3+mx2+1(m≠0) 在区间 (0,2) 上的极大值为最大值,则m的取值范围是(??? )
A.?(0,3)?????????????????????????????B.?(?3,0)?????????????????????????????C.?(?∞,?3)?????????????????????????????D.?(3,+∞)
5.若函数 f(x)=asinx+13sin3x 在 x=π3 处有最大(小)值,则a等于(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?233??????????????????????????????????????????D.?0
6.若函数 f(x)=12x2+(a?1)x?alnx 存在唯一的极值,且此极值不小于1,则 a 的取值范围为(? )
A.?[32,2)?????????????????????????B.?[32,+∞)?????????????????????????C.?[0,32)?????????????????????????D.?(?1,0)∪[32,+∞)
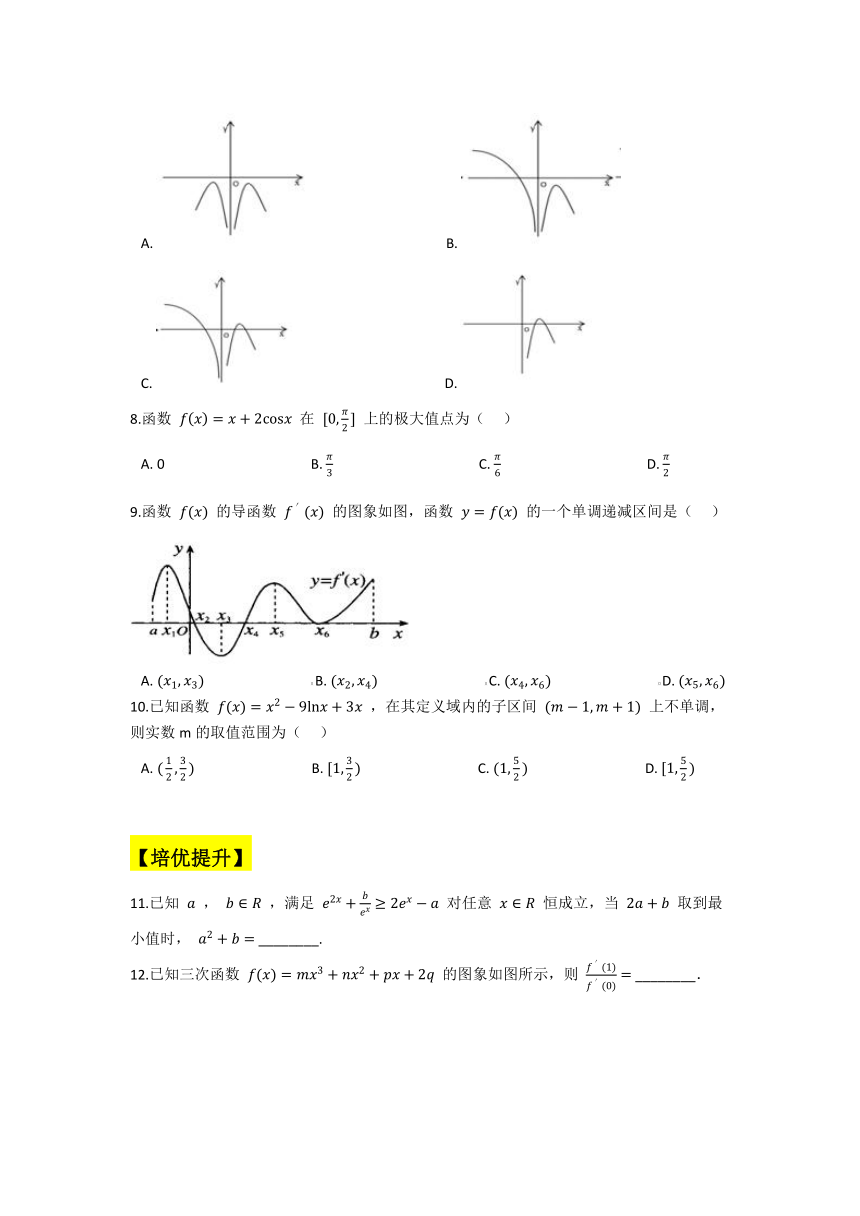
7.函数 f(x)=lnx2?x 的图象大致为(??? )
A.?????????????????????????????????????????B.?
C.????????????????????????????????????????????D.?
8.函数 fx=x+2cosx 在 [0,π2] 上的极大值点为(??? )
A.?0??????????????????????????????????????????B.?π3??????????????????????????????????????????C.?π6??????????????????????????????????????????D.?π2
9.函数 f(x) 的导函数 f′(x) 的图象如图,函数 y=f(x) 的一个单调递减区间是(??? )
A.?(x1,x3)???????????????????????????????B.?(x2,x4)???????????????????????????????C.?(x4,x6)???????????????????????????????D.?(x5,x6)
10.已知函数 f(x)=x2?9lnx+3x ,在其定义域内的子区间 (m?1,m+1) 上不单调,则实数m的取值范围为(??? )
A.?(12,32)??????????????????????????????????B.?[1,32)??????????????????????????????????C.?(1,52)??????????????????????????????????D.?[1,52)
【培优提升】
11.已知 a , b∈R ,满足 e2x+bex≥2ex?a 对任意 x∈R 恒成立,当 2a+b 取到最小值时, a2+b= ________.
12.已知三次函数 f(x)=mx3+nx2+px+2q 的图象如图所示,则 f′(1)f′(0)= ________.
13.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是________.
14.函数 f(x)=x3?3x2?9x?1 的图象与函数 g(x)=a 的图象有三个交点,则实数 a 的取值范围是________.
15.已知函数 f(x)=12x2?2ax+2alnx(a∈R) .
(1)若函数 f(x) 在 (0,+∞) 内是单调函数,求实数 a 的取值范围;
(2)已知 x1 、 x2 是函数 f(x) 的两个极值点,当 x2>ex1 时,均有 f(x1)?λ2x12>f(x2)?λ2x22 成立,求实数 λ 的取值范围( e 为自然对数的底数)
16.已知函数 f(x)=ex?ax?1 .
(1)讨论函数 f(x) 的单调性;
(2)若函数 f(x) 在 (0,+∞) 有零点 x0 ,求证:
(ⅰ) 2lnaa(ⅱ) f(ax0)>(a?1)3(a+1) .
17.已知函数 f(x)=ex , g(x)=lnx .
(Ⅰ)若函数 ?(x)=f(x)+ag(x) 存在极小值,求实数 a 的取值范围;
(Ⅱ)若 m>0 ,且 m2x2f(x?1)?(x+1)g(x)?mx≥0 对任意 x>0 恒成立,求实数 m 的取值范围.
(参考数据: ln2≈0.69 , e≈2.718 )
18.已知函数 f(x)=(m+1)lnx , g(x)=mx2+x , m∈R .
(1)当 m=0 时,曲线 ?(x)=f(x)+ag(x)?1?(a∈R) 在 x=2 处的切线与直线 x+2y?1=0 平行,求函数 y=?(x) 在 [e,?e2] 上的最大值( e 为自然对数的底数);
(2)当 m=1 时,已知 04ag(a)+g(b)?a?b .
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 C
4.【答案】 A
5.【答案】 A
6.【答案】 B
7.【答案】 B
8.【答案】 C
9.【答案】 B
10.【答案】 D
11.【答案】 24
12.【答案】 1
13.【答案】 (0,1)
14.【答案】 (-28,4)
15.【答案】 (1)解:函数 f(x)=12x2?2ax+2alnx 的定义域为 (0,+∞) ,且 f′(x)=x?2a+2ax=x2?2ax+2ax .
设 g(x)=x2?2ax+2a .
(i)若函数 f(x) 在 (0,+∞) 内单调递增,则对任意的 x∈(0,+∞) , g(x)≥0 .
二次函数 g(x) 的图象开口向上,对称轴为直线 x=a .
①若 a≤0 ,则函数 g(x) 在 (0,+∞) 上单调递增,所以 g(0)=2a≥0 ,解得 a≥0 ,此时 a=0 ;
②若 a>0 ,由题意可得 Δ=4a2?8a≤0 ,解得 0≤a≤2 ,此时, 0所以,当 0≤a≤2 时,函数 f(x) 在 (0,+∞) 上为增函数.
(ii)若函数 f(x) 在 (0,+∞) 内单调递减,则对任意的 x>0 , g(x)≤0 ,
若 Δ≤0 ,则对任意的 x>0 , g(x)≥0 ,不合乎题意;
若 Δ>0 ,解不等式 g(x)≤0 ,即 x2?2ax+2a≤0 ,解得 a?a2?2a≤x≤a+a2?2a ,不合乎题意.
综上所述,实数 a 的取值范围是 [0,2]
(2)解:由题意可知, x1 、 x2 是方程 x2?2ax+2a=0 的两个正根,则 {Δ=4a2?8a>0a>0g(0)=2a>0 ,解得 a>2 .
由韦达定理可得 x1+x2=x1x2=2a .
f(x2)?f(x1)=(12x22?2ax2+2alnx2)?(12x12?2ax1+2alnx1) =2alnx2x1+12(x22?x12)?2a(x2?x1)
=x1x2lnx2x1+12(x22?x12)?(x2+x1)(x2?x1)=x1x2lnx2x1?12(x22?x12) ,
由 f(x1)?λ2x12>f(x2)?λ2x22 ,可得 f(x2)?f(x1)?λ2(x22?x12)<0 ,
即 x1x2lnx2x1?λ+12(x22?x12)<0 ,即 lnx2x1?λ+12(x2x1?x1x2)<0 ,
即 λ+12(x2x1?x1x2)?lnx2x1>0 ,
令 t=x2x1>e ,可得 λ+12(t?1t)?lnt>0 ,可得 λ+12>lntt?1t=tlntt2?1 ,
令 ?(t)=tlntt2?1 ,其中 t>e , ?′(t)=(lnt+1)(t2?1)?2t2lnt(t2?1)2=(t2?1)?(t2+1)lnt(t2?1)2<0 ,
所以,函数 ?(t) 在区间 (e,+∞) 上单调递减,当 t>e 时, ?(t)所以, λ+12≥ee2?1 ,解得 λ≥2e+1?e2e2?1 .
综上所述,实数 λ 的取值范围是 [2e+1?e2e2?1,+∞)
16.【答案】 (1)解: f(x)=ex?ax?1?f′(x)=ex?a
①当 a≤0 时, f′(x)=ex?a>0 , f(x) 在R上单调递增;
②当 a>0 时, f′(x)=ex?a=0?x=lna ,
所以 f(x) 在 (?∞,lna) 上单调递减,在 (lna,+∞) 上单调递增
(2)解:(ⅰ)由题意可得 a=ex0?1x0 ,
要证明 x0<2lna ,只要证明 ex02设 g(x)=ex?xex2?1 , x>0
g′(x)=ex?ex2?x2ex2=ex2(ex2?1?x2)≥0 ,
所以 g(x)=ex?xex2?1 在 (0,+∞) 上递增,所以 g(x)>g(0)=0 ,得证.
要证明 x0>2lnaa ,只要证明 ex0?1>2lnex0?1x0 ,
设 ?(x)=ex?1?2lnex?1x , x>0
?′(x)=ex?2(xex?ex+1)x(ex?1)=e2x+ex?2xex?2x(ex?1) ,
φ(x)=ex?2x+1?2e?x , x>0
φ′(x)=ex?2+2e?x>0 ,
所以 φ(x)=ex?2x+1?2e?x>φ(0)=0 ,所以 ?′(x)≥0 ,
当 x→0+ 时, ?(x)→0 , ?(x)>0 ,得证.
(ⅱ)因为 2lnaa2lna>lna ,
又 f(x) 在 (lna,+∞) 上单调递增, f(ax0)>f(2lna)=a2?2alna?1 ,
设 k(x)=x2?2xlnx?1?(x?1)3(x+1)(x>1) ,
k′(x)=?2?2lnx+3x?1x ,且 k′(1)=0 ,
设 p(x)=?2?2lnx+3x?1x ,则
p′(x)=?2x+32x+12xx=3x?2x+12xx>0 , p(x) 递增,即 k′(x) 递增,
故 k(x)>k(1)=0 ,?
所以, f(ax0)>(a?1)3(a+1)
17.【答案】 解:(Ⅰ)由题得 ?(x)=ex+alnx , ?′(x)=ex+ax=xex+ax
又 φ(x)=xex 在 (0,+∞) 上为单调递增函数, φ(0)=0 ,
故当 a≥0 时, ?(x) 无极值.
当 a<0 时,存在 x0>0 , ?(x) 在 (0,x0) 上单调递增, (x0,+∞) 上单调递增,存在极小值故 a<0 .
(Ⅱ)由 m2x2f(x?1)?(x+1)g(x)?mx≥0 即 m2x2ex?1?(x+1)lnx?mx≥0
首先,令 x=1 ,得 m≥1 ;
下面证明当 m≥1 时符合要求:
令 t(m)=m2x2ex?1?(x+1)lnx?mx .
⑴若 x2x2ex?1=12xex?1≤1 ,即 xex?1≥12 时,
t(m)≥t(1)=x2ex?1?(x+1)lnx?x .
令 k(x)=x2ex?1?(x+1)lnx?x .
得 k′(x)=(x2+2x)ex?1?1x?lnx?2 .
k″(x)=(x2+4x+2)ex?1+1x2?1x≥(x4+4x+2)?12x+1x2?1x=x2+1x2+2 .
显然当 x>0 时, k′(0)>0 ,从而 k′(x) 递增,又 k′(1)=0
则 0x>1 时, k′(x)>0 , k(x) 在 (1,+∞) 上单调递增,
所以 kmin(x)=k(1)=0 得证;
⑵若 x2x2ex?1=12xex?1>1 ,即 xex?1<12 时,
t(m)≥t(12xex?1)=?4ex?1(x+1)lnx+14ex?1 .
下面,只要证 n(x)=4ex?1(x+1)lnx+1≤0 ,其中 xex?1<12 .
由 xex?1<12 ,且 y=xex?1 在 (0,+∞) 上单调递增,记 x0ex0?1=12 ,得 x∈(0,x0)
又 (1?ln2)e(1?ln2)?1<12 ,所以 x0>1?ln2
又 n(x)≤4ex?1(x+1)(x?1)+1=4x2ex?1?4ex?1+1<2x?4ex?1+1 .
令 p(x)=2x?4ex?1+1 ,则 p′(x)=2?4ex?1 .
所以当 x∈(0,x0) 时, p(x) 在 (0,1?ln2) 上单调递增, (1?ln2,x0) 上单调递减,
p(x)≤p(1?ln2)=1?2ln2<0 ,得证.
故所求实数 m 的取值范围为 m≥1 .
18.【答案】 (1)解:当 m=0 时, ?(x)=lnx+ax?1 ,因此 ?'(x)=1x?ax2 ,
而曲线 y=?(x) 在 x=2 处的切线与直线 x+2y?1=0 平行,
故 ?'(2)=12?a4=?12 ,解得 a=4 .
所以 ?(x)=lnx+4x?1 , ?'(x)=x?4x2 ,
故当 x∈[e,?4) 时, ?'(x)<0 ,即函数 y=?(x) 在 [e,?4) 上递减,
当 x∈(4,?e2] 时, ?'(x)>0 ,即函数 y=?(x) 在 (4,?e2] 上递增,
所以 [?(x)]max=max{?(e),??(e2)} ,而 ?(e)=4e , ?(e2)=4e2+1 ,
故 ?(e2)??(e)=(e?2)2e2>0 ,即 ?(e2)>?(e) ,
所以函数 y=?(x) 在 [e,?e2] 上的最大值为 4e2+1
(2)证明:当 m=1 时, f(x)=2lnx , g(x)=x2+x ,由于 0故要证明 f(a)?f(b)a?b>4ag(a)+g(b)?a?b 成立.
? 证明 lnb?lnab?a>2aa2+b2 成立 ? 证明 lnb?lna>2a(b?a)a2+b2 成立,
? 证明 lnba>2(ba?1)(ba)2+1 成立.令 x=ba ,因为 01 ,
即只需证明 lnx>2(x?1)x2+1?(x>1) 成立
? 证明 (x2+1)lnx?2x+2>0?(x>1) 即可,下面证明该不等式成立.
设 F(x)=(x2+1)lnx?2x+2?(x>1) ,求得 F'(x)=2xlnx+x+1x?2 ,
因为 x>1 ,所以 x+1x>2x?1x=2 ,
所以当 x>1 时, F'(x)>2xlnx+2?2=2xlnx>0 ,
因此函数 y=F(x) 是 (1,?+∞) 上的增函数,故 F(x)>F(1)=0 ,
这就证明了当 x>1 时, (x2+1)lnx?2x+2>0 恒成立,故原命题成立
【5.3导数在研究函数中的应用专题训练】
【基础巩固】
1.已知函数 f(x)={ex?1?1,x≥1,lnx,0
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.已知函数 f(x)=x3?12x,x∈[?3,3] ,则 f(x) 的最大值为(??? )
A.?-9?????????????????????????????????????????B.?-16?????????????????????????????????????????C.?16?????????????????????????????????????????D.?9
3.已知 f(x)=lnx+ax(a≠0) ,则( ??)
A.?当 a<0 时, f(x) 存在极小值 f(a)???????????????????B.?当 a<0 时, f(x) 存在极大值 f(a)
C.?当 a>0 时, f(x) 存在极小值 f(a)???????????????????D.?当 a>0 时, f(x) 存在极大值 f(a)
4.若函数 f(x)=?x3+mx2+1(m≠0) 在区间 (0,2) 上的极大值为最大值,则m的取值范围是(??? )
A.?(0,3)?????????????????????????????B.?(?3,0)?????????????????????????????C.?(?∞,?3)?????????????????????????????D.?(3,+∞)
5.若函数 f(x)=asinx+13sin3x 在 x=π3 处有最大(小)值,则a等于(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?233??????????????????????????????????????????D.?0
6.若函数 f(x)=12x2+(a?1)x?alnx 存在唯一的极值,且此极值不小于1,则 a 的取值范围为(? )
A.?[32,2)?????????????????????????B.?[32,+∞)?????????????????????????C.?[0,32)?????????????????????????D.?(?1,0)∪[32,+∞)
7.函数 f(x)=lnx2?x 的图象大致为(??? )
A.?????????????????????????????????????????B.?
C.????????????????????????????????????????????D.?
8.函数 fx=x+2cosx 在 [0,π2] 上的极大值点为(??? )
A.?0??????????????????????????????????????????B.?π3??????????????????????????????????????????C.?π6??????????????????????????????????????????D.?π2
9.函数 f(x) 的导函数 f′(x) 的图象如图,函数 y=f(x) 的一个单调递减区间是(??? )
A.?(x1,x3)???????????????????????????????B.?(x2,x4)???????????????????????????????C.?(x4,x6)???????????????????????????????D.?(x5,x6)
10.已知函数 f(x)=x2?9lnx+3x ,在其定义域内的子区间 (m?1,m+1) 上不单调,则实数m的取值范围为(??? )
A.?(12,32)??????????????????????????????????B.?[1,32)??????????????????????????????????C.?(1,52)??????????????????????????????????D.?[1,52)
【培优提升】
11.已知 a , b∈R ,满足 e2x+bex≥2ex?a 对任意 x∈R 恒成立,当 2a+b 取到最小值时, a2+b= ________.
12.已知三次函数 f(x)=mx3+nx2+px+2q 的图象如图所示,则 f′(1)f′(0)= ________.
13.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是________.
14.函数 f(x)=x3?3x2?9x?1 的图象与函数 g(x)=a 的图象有三个交点,则实数 a 的取值范围是________.
15.已知函数 f(x)=12x2?2ax+2alnx(a∈R) .
(1)若函数 f(x) 在 (0,+∞) 内是单调函数,求实数 a 的取值范围;
(2)已知 x1 、 x2 是函数 f(x) 的两个极值点,当 x2>ex1 时,均有 f(x1)?λ2x12>f(x2)?λ2x22 成立,求实数 λ 的取值范围( e 为自然对数的底数)
16.已知函数 f(x)=ex?ax?1 .
(1)讨论函数 f(x) 的单调性;
(2)若函数 f(x) 在 (0,+∞) 有零点 x0 ,求证:
(ⅰ) 2lnaa
17.已知函数 f(x)=ex , g(x)=lnx .
(Ⅰ)若函数 ?(x)=f(x)+ag(x) 存在极小值,求实数 a 的取值范围;
(Ⅱ)若 m>0 ,且 m2x2f(x?1)?(x+1)g(x)?mx≥0 对任意 x>0 恒成立,求实数 m 的取值范围.
(参考数据: ln2≈0.69 , e≈2.718 )
18.已知函数 f(x)=(m+1)lnx , g(x)=mx2+x , m∈R .
(1)当 m=0 时,曲线 ?(x)=f(x)+ag(x)?1?(a∈R) 在 x=2 处的切线与直线 x+2y?1=0 平行,求函数 y=?(x) 在 [e,?e2] 上的最大值( e 为自然对数的底数);
(2)当 m=1 时,已知 0
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 C
4.【答案】 A
5.【答案】 A
6.【答案】 B
7.【答案】 B
8.【答案】 C
9.【答案】 B
10.【答案】 D
11.【答案】 24
12.【答案】 1
13.【答案】 (0,1)
14.【答案】 (-28,4)
15.【答案】 (1)解:函数 f(x)=12x2?2ax+2alnx 的定义域为 (0,+∞) ,且 f′(x)=x?2a+2ax=x2?2ax+2ax .
设 g(x)=x2?2ax+2a .
(i)若函数 f(x) 在 (0,+∞) 内单调递增,则对任意的 x∈(0,+∞) , g(x)≥0 .
二次函数 g(x) 的图象开口向上,对称轴为直线 x=a .
①若 a≤0 ,则函数 g(x) 在 (0,+∞) 上单调递增,所以 g(0)=2a≥0 ,解得 a≥0 ,此时 a=0 ;
②若 a>0 ,由题意可得 Δ=4a2?8a≤0 ,解得 0≤a≤2 ,此时, 0
(ii)若函数 f(x) 在 (0,+∞) 内单调递减,则对任意的 x>0 , g(x)≤0 ,
若 Δ≤0 ,则对任意的 x>0 , g(x)≥0 ,不合乎题意;
若 Δ>0 ,解不等式 g(x)≤0 ,即 x2?2ax+2a≤0 ,解得 a?a2?2a≤x≤a+a2?2a ,不合乎题意.
综上所述,实数 a 的取值范围是 [0,2]
(2)解:由题意可知, x1 、 x2 是方程 x2?2ax+2a=0 的两个正根,则 {Δ=4a2?8a>0a>0g(0)=2a>0 ,解得 a>2 .
由韦达定理可得 x1+x2=x1x2=2a .
f(x2)?f(x1)=(12x22?2ax2+2alnx2)?(12x12?2ax1+2alnx1) =2alnx2x1+12(x22?x12)?2a(x2?x1)
=x1x2lnx2x1+12(x22?x12)?(x2+x1)(x2?x1)=x1x2lnx2x1?12(x22?x12) ,
由 f(x1)?λ2x12>f(x2)?λ2x22 ,可得 f(x2)?f(x1)?λ2(x22?x12)<0 ,
即 x1x2lnx2x1?λ+12(x22?x12)<0 ,即 lnx2x1?λ+12(x2x1?x1x2)<0 ,
即 λ+12(x2x1?x1x2)?lnx2x1>0 ,
令 t=x2x1>e ,可得 λ+12(t?1t)?lnt>0 ,可得 λ+12>lntt?1t=tlntt2?1 ,
令 ?(t)=tlntt2?1 ,其中 t>e , ?′(t)=(lnt+1)(t2?1)?2t2lnt(t2?1)2=(t2?1)?(t2+1)lnt(t2?1)2<0 ,
所以,函数 ?(t) 在区间 (e,+∞) 上单调递减,当 t>e 时, ?(t)所以, λ+12≥ee2?1 ,解得 λ≥2e+1?e2e2?1 .
综上所述,实数 λ 的取值范围是 [2e+1?e2e2?1,+∞)
16.【答案】 (1)解: f(x)=ex?ax?1?f′(x)=ex?a
①当 a≤0 时, f′(x)=ex?a>0 , f(x) 在R上单调递增;
②当 a>0 时, f′(x)=ex?a=0?x=lna ,
所以 f(x) 在 (?∞,lna) 上单调递减,在 (lna,+∞) 上单调递增
(2)解:(ⅰ)由题意可得 a=ex0?1x0 ,
要证明 x0<2lna ,只要证明 ex02
g′(x)=ex?ex2?x2ex2=ex2(ex2?1?x2)≥0 ,
所以 g(x)=ex?xex2?1 在 (0,+∞) 上递增,所以 g(x)>g(0)=0 ,得证.
要证明 x0>2lnaa ,只要证明 ex0?1>2lnex0?1x0 ,
设 ?(x)=ex?1?2lnex?1x , x>0
?′(x)=ex?2(xex?ex+1)x(ex?1)=e2x+ex?2xex?2x(ex?1) ,
φ(x)=ex?2x+1?2e?x , x>0
φ′(x)=ex?2+2e?x>0 ,
所以 φ(x)=ex?2x+1?2e?x>φ(0)=0 ,所以 ?′(x)≥0 ,
当 x→0+ 时, ?(x)→0 , ?(x)>0 ,得证.
(ⅱ)因为 2lnaa
又 f(x) 在 (lna,+∞) 上单调递增, f(ax0)>f(2lna)=a2?2alna?1 ,
设 k(x)=x2?2xlnx?1?(x?1)3(x+1)(x>1) ,
k′(x)=?2?2lnx+3x?1x ,且 k′(1)=0 ,
设 p(x)=?2?2lnx+3x?1x ,则
p′(x)=?2x+32x+12xx=3x?2x+12xx>0 , p(x) 递增,即 k′(x) 递增,
故 k(x)>k(1)=0 ,?
所以, f(ax0)>(a?1)3(a+1)
17.【答案】 解:(Ⅰ)由题得 ?(x)=ex+alnx , ?′(x)=ex+ax=xex+ax
又 φ(x)=xex 在 (0,+∞) 上为单调递增函数, φ(0)=0 ,
故当 a≥0 时, ?(x) 无极值.
当 a<0 时,存在 x0>0 , ?(x) 在 (0,x0) 上单调递增, (x0,+∞) 上单调递增,存在极小值故 a<0 .
(Ⅱ)由 m2x2f(x?1)?(x+1)g(x)?mx≥0 即 m2x2ex?1?(x+1)lnx?mx≥0
首先,令 x=1 ,得 m≥1 ;
下面证明当 m≥1 时符合要求:
令 t(m)=m2x2ex?1?(x+1)lnx?mx .
⑴若 x2x2ex?1=12xex?1≤1 ,即 xex?1≥12 时,
t(m)≥t(1)=x2ex?1?(x+1)lnx?x .
令 k(x)=x2ex?1?(x+1)lnx?x .
得 k′(x)=(x2+2x)ex?1?1x?lnx?2 .
k″(x)=(x2+4x+2)ex?1+1x2?1x≥(x4+4x+2)?12x+1x2?1x=x2+1x2+2 .
显然当 x>0 时, k′(0)>0 ,从而 k′(x) 递增,又 k′(1)=0
则 0
所以 kmin(x)=k(1)=0 得证;
⑵若 x2x2ex?1=12xex?1>1 ,即 xex?1<12 时,
t(m)≥t(12xex?1)=?4ex?1(x+1)lnx+14ex?1 .
下面,只要证 n(x)=4ex?1(x+1)lnx+1≤0 ,其中 xex?1<12 .
由 xex?1<12 ,且 y=xex?1 在 (0,+∞) 上单调递增,记 x0ex0?1=12 ,得 x∈(0,x0)
又 (1?ln2)e(1?ln2)?1<12 ,所以 x0>1?ln2
又 n(x)≤4ex?1(x+1)(x?1)+1=4x2ex?1?4ex?1+1<2x?4ex?1+1 .
令 p(x)=2x?4ex?1+1 ,则 p′(x)=2?4ex?1 .
所以当 x∈(0,x0) 时, p(x) 在 (0,1?ln2) 上单调递增, (1?ln2,x0) 上单调递减,
p(x)≤p(1?ln2)=1?2ln2<0 ,得证.
故所求实数 m 的取值范围为 m≥1 .
18.【答案】 (1)解:当 m=0 时, ?(x)=lnx+ax?1 ,因此 ?'(x)=1x?ax2 ,
而曲线 y=?(x) 在 x=2 处的切线与直线 x+2y?1=0 平行,
故 ?'(2)=12?a4=?12 ,解得 a=4 .
所以 ?(x)=lnx+4x?1 , ?'(x)=x?4x2 ,
故当 x∈[e,?4) 时, ?'(x)<0 ,即函数 y=?(x) 在 [e,?4) 上递减,
当 x∈(4,?e2] 时, ?'(x)>0 ,即函数 y=?(x) 在 (4,?e2] 上递增,
所以 [?(x)]max=max{?(e),??(e2)} ,而 ?(e)=4e , ?(e2)=4e2+1 ,
故 ?(e2)??(e)=(e?2)2e2>0 ,即 ?(e2)>?(e) ,
所以函数 y=?(x) 在 [e,?e2] 上的最大值为 4e2+1
(2)证明:当 m=1 时, f(x)=2lnx , g(x)=x2+x ,由于 0
? 证明 lnb?lnab?a>2aa2+b2 成立 ? 证明 lnb?lna>2a(b?a)a2+b2 成立,
? 证明 lnba>2(ba?1)(ba)2+1 成立.令 x=ba ,因为 0
即只需证明 lnx>2(x?1)x2+1?(x>1) 成立
? 证明 (x2+1)lnx?2x+2>0?(x>1) 即可,下面证明该不等式成立.
设 F(x)=(x2+1)lnx?2x+2?(x>1) ,求得 F'(x)=2xlnx+x+1x?2 ,
因为 x>1 ,所以 x+1x>2x?1x=2 ,
所以当 x>1 时, F'(x)>2xlnx+2?2=2xlnx>0 ,
因此函数 y=F(x) 是 (1,?+∞) 上的增函数,故 F(x)>F(1)=0 ,
这就证明了当 x>1 时, (x2+1)lnx?2x+2>0 恒成立,故原命题成立
