5.2 运动的合成与分解同步练习 —2020-2021学年【新教材】人教版(2019)高中物理必修二(word版含答案)
文档属性
| 名称 | 5.2 运动的合成与分解同步练习 —2020-2021学年【新教材】人教版(2019)高中物理必修二(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 365.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-15 20:50:13 | ||
图片预览



文档简介
运动的合成与分解练习
一、单选题
对于两个分运动及其合运动,下列说法正确的是(????)
A. 合运动的速度一定比两个分运动的速度都大
B. 合运动的速度至少比其中一个分运动的速度大
C. 合运动的速度方向就是物体实际运动的方向
D. 合运动的时间一定比分运动的时间长
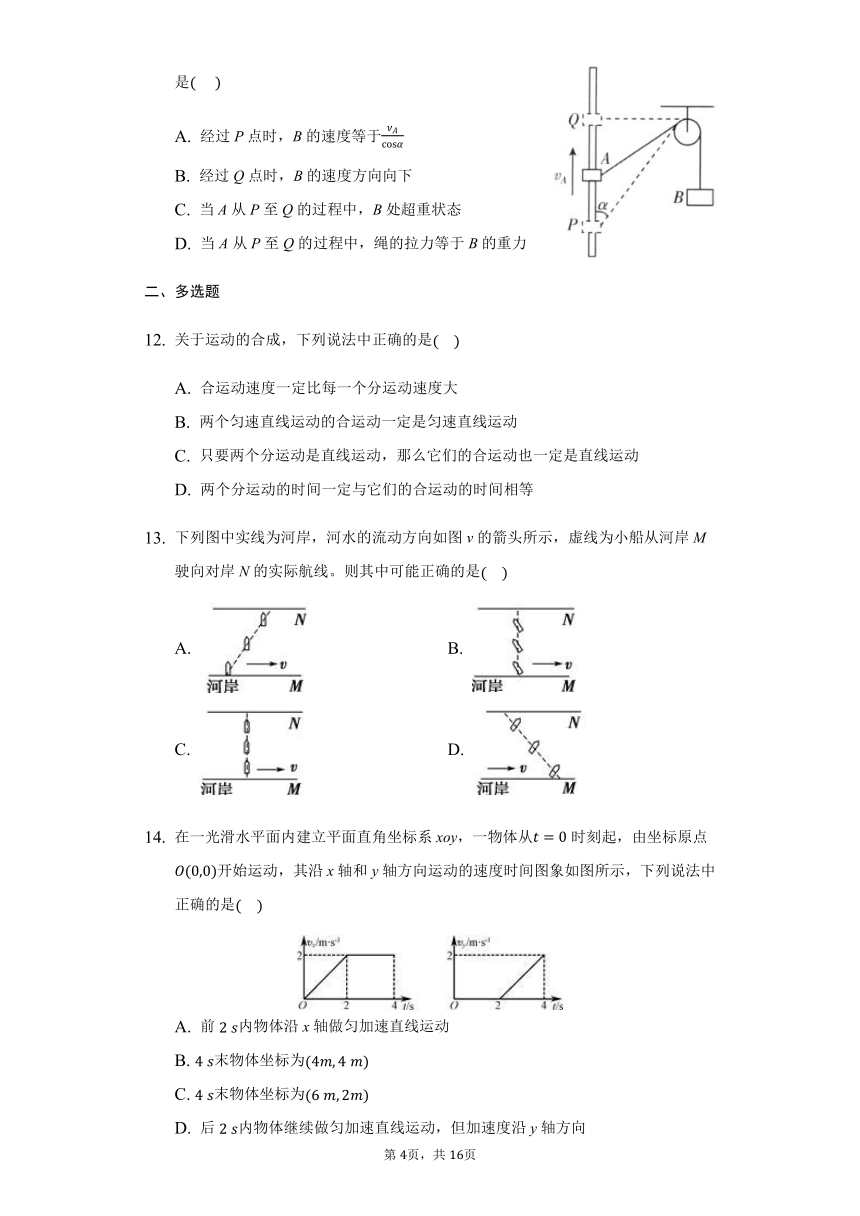
如图所示,一条小船位于200?m宽的河中央A点处,离A点距离为1003m的下游处有一危险的急流区,当时水流速度为4?m/s,为使小船避开危险区沿直线到达对岸,小船在静止水中的速度至少为(????)
A. 433m/s B. 833m/s C. 2?m/s D. 4?m/s
如下图所示,有人在河面上方20m的岸上用跨过定滑轮的长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率ν=3m/s拉绳使小船靠岸,那么(??? )
A. 5s时绳与水面的夹角为60° B. 5s时小船前进了15m
C. 5s时小船的速率为5m/s D. 5s时小船到岸边距离为10m
甲、乙两船在同一河流中同时开始渡河,河水流速为v0。两船在静水中的速率均为,甲、乙两船船头均与河岸夹角为,如图所示,已知甲船恰好能垂直到达河正对岸的点,乙船到达河对岸的点,A,B之间的距离为。则下列判断错误的是(??? )
A. 甲、乙两船同时到达对岸
B. 若仅是河水流速v0增大,则两船的渡河时间都不变
C. 不论河水流速v0如何改变,只要适当改变角,甲船总能到达正对岸的点
D. 若仅是河水流速v0增大,则两船到达对岸时,两船之间的距离仍然为
质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动当小车与滑轮间的细绳和水平方向成夹角θ2时(如图),下列判断正确的是(? ? ? ?).
A. P的速率为v B. P的速率为vcosθ2
C. 绳的拉力等于mgsinθ1 D. 绳的拉力小于mgsinθ1
物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图象如图所示,则对该物体运动过程的描述正确的是(????)
A. 物体在0~3?s做匀变速直线运动 B. 物体在0~3?s做匀变速曲线运动
C. 物体在3~4?s做变加速直线运动 D. 物体在3~4?s做匀变速曲线运动
有一条两岸平直、河水均匀流动、流速恒为v的大河。小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直。去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为(????)
A. v1?k2 B. kvk2?1 C. kv1?k2 D. vk2?1
直角坐标系xOy在水平面内,一物体的运动规律是x=3t2m;y=4t2m(t的单位为s),则下列说法中正确的是(??? )
①物体在x和y方向上都是做初速度为零的匀加速运动
②物体的合运动是初速度为零、加速度为5m/s2的匀加速直线运动
③物体的合运动是初速度为零、加速度为10m/s2的匀加速直线运动
④物体的合运动是加速度为5m/s2的曲线运动
A. ①② B. ①③ C. ②③ D. ②④
在第十一届珠海国际航展上,歼?20战机是此次航展最大的“明星”.如图所示,歼?20战机在降落过程中水平方向的初速度为60m/s,竖直方向的初速度为6m/s,已知歼?20战机在水平方向做加速度大小为2m/s2的匀减速直线运动,在竖直方向做加速度大小为0.2m/s2的匀减速直线运动,则歼?20战机在降落过程中,下列说法正确的是(??? )
A. 歼?20战机的运动轨迹为曲线
B. 经20s,歼?20战机水平方向的分速度与竖直方向的分速度大小相等
C. 在前20s内,歼?20战机在水平方向的分位移与竖直方向的分位移大小相等
D. 歼?20战机在前20s内,水平方向的平均速度为40m/s
如图所示,在一次救灾工作中,一架离水面高为H、沿水平直线飞行的直升机A,用悬索(重力可忽略不计)救护困在湖水中的伤员B,在直升机A和伤员B以相同的水平速率匀速运动的同时,悬索将伤员吊起.设经t时间后,A,B之间的距离为l,且l=H?t2,则在这段时间内伤员B的受力情况和运动轨迹是哪个图(??? )
A. B. C. D.
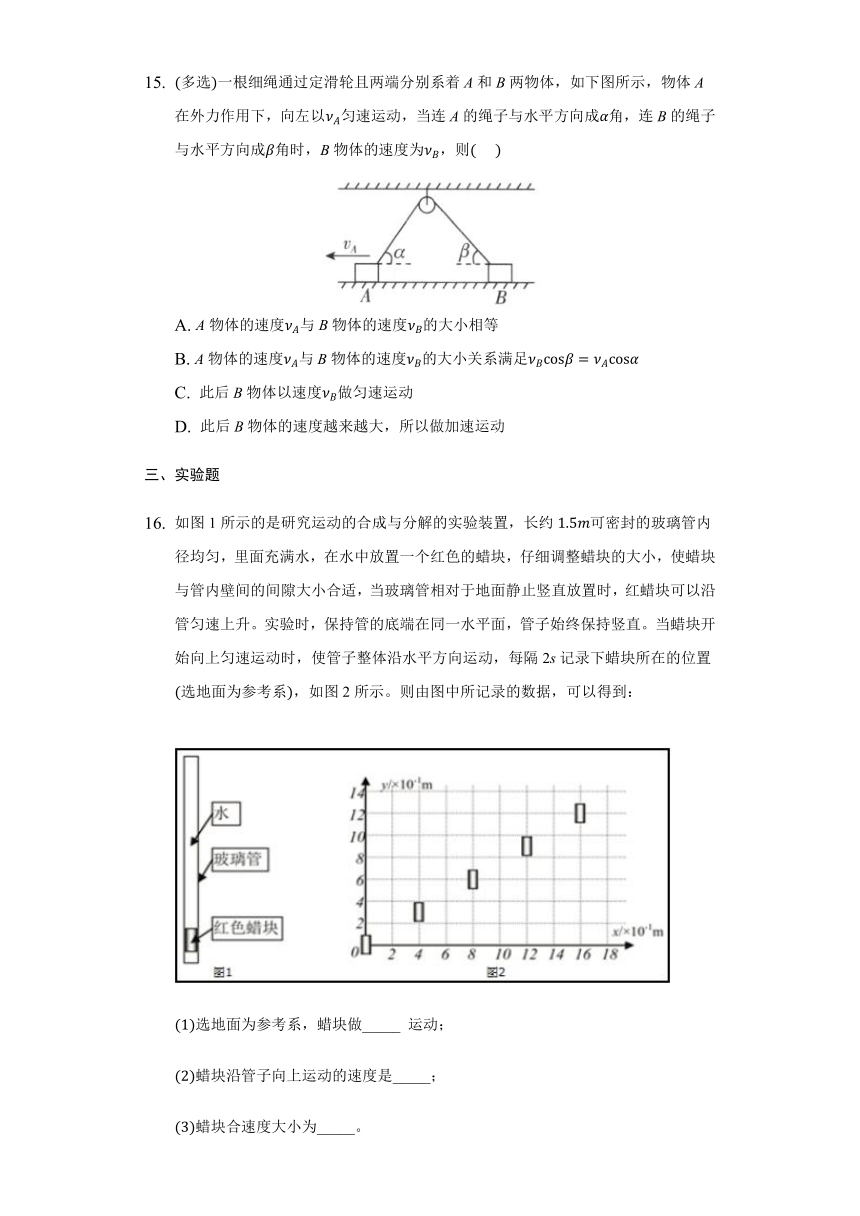
如下图所示,套在竖直固定细杆上的环A由跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度νA匀速上升经过P、Q两点,经过P点时绳与竖直杆间的夹角为α,经过Q点时A与定滑轮的连线处于水平方向,则下列说法正确的是(??? )
A. 经过P点时,B的速度等于νAcosα
B. 经过Q点时,B的速度方向向下
C. 当A从P至Q的过程中,B处超重状态
D. 当A从P至Q的过程中,绳的拉力等于B的重力
二、多选题
关于运动的合成,下列说法中正确的是(????)
A. 合运动速度一定比每一个分运动速度大
B. 两个匀速直线运动的合运动一定是匀速直线运动
C. 只要两个分运动是直线运动,那么它们的合运动也一定是直线运动
D. 两个分运动的时间一定与它们的合运动的时间相等
下列图中实线为河岸,河水的流动方向如图v的箭头所示,虚线为小船从河岸M驶向对岸N的实际航线。则其中可能正确的是(????)
A. B.
C. D.
在一光滑水平面内建立平面直角坐标系xoy,一物体从t=0时刻起,由坐标原点O(0,0)开始运动,其沿x轴和y轴方向运动的速度时间图象如图所示,下列说法中正确的是(????)
A. 前2?s内物体沿x轴做匀加速直线运动
B. 4?s末物体坐标为(4m,4?m)
C. 4?s末物体坐标为(6?m,2m)
D. 后2?s内物体继续做匀加速直线运动,但加速度沿y轴方向
(多选)一根细绳通过定滑轮且两端分别系着A和B两物体,如下图所示,物体A在外力作用下,向左以νA匀速运动,当连A的绳子与水平方向成α角,连B的绳子与水平方向成β角时,B物体的速度为νB,则(??? )
A. A物体的速度νA与B物体的速度νB的大小相等
B. A物体的速度νA与B物体的速度νB的大小关系满足νBcosβ=νAcosα
C. 此后B物体以速度νB做匀速运动
D. 此后B物体的速度越来越大,所以做加速运动
三、实验题
如图1所示的是研究运动的合成与分解的实验装置,长约1.5m可密封的玻璃管内径均匀,里面充满水,在水中放置一个红色的蜡块,仔细调整蜡块的大小,使蜡块与管内壁间的间隙大小合适,当玻璃管相对于地面静止竖直放置时,红蜡块可以沿管匀速上升。实验时,保持管的底端在同一水平面,管子始终保持竖直。当蜡块开始向上匀速运动时,使管子整体沿水平方向运动,每隔2s记录下蜡块所在的位置(选地面为参考系),如图2所示。则由图中所记录的数据,可以得到:
(1)选地面为参考系,蜡块做_____ 运动;
(2)蜡块沿管子向上运动的速度是_____;
(3)蜡块合速度大小为_____。
如图甲所示,实验小组在竖直放置的两端封闭的玻璃管中注满清水,内有一个圆柱形的红蜡块能从坐标圆点O在水中匀速上浮。现进行如下操作:
??? 操作一:当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平向右匀速运动,测得红蜡块运动到顶端所需时间为t1。
??? 操作二:当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管从静止水平向右做匀加速直线运动,测得红蜡块从下端运动到顶端所需时间为t2。
根据以上信息,回答下列问题:
(1)t1________t2(选填“大于”、“小于”或“等于”);
(2)在图乙中,能正确反映操作一中红蜡块上升过程中运动轨迹的示意图是________;能正确反映操作二中红蜡块上升过程中运动轨迹的示意图是________。
四、计算题
一辆车通过一根跨过光滑轻质定滑轮的轻绳提升一个质量为m的重物,开始车在滑轮的正下方,绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速直线运动,经过时间t绳子与水平方向的夹角为θ,如图所示.试求:
?
(1)车向左运动的加速度的大小;
(2)重物m在t时刻速度的大小.
小船在200m宽的河中航行,水流速度为2m/s,船在静水中的速度为4m/s.已知cos53°=35.
(1)若小船在河中垂直于河岸航行,小船将在何时、何处到达对岸?
(2)小船怎样过河用时最短?过河的最短时间为多少?
(3)要使小船到达正对岸,应如何航行?历时多久?
(4)若水流速度是5m/s,船在静水中的速度是3m/s,则怎样过河才能使船沿河岸方向航行的距离最小?该最小距离是多少?
如下图所示,甲图表示某物体在x轴上分速度的νx?t图像,乙图表示该物体在y轴方向上分速度的νy?t图像.求:
? ? ? ? ? ?
? ? ? ? ?甲? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?乙
(1)在t=0时刻物体的速度大小;
(2)在t=8s时刻物体的速度大小;
(3)在0~4s内物体的位移大小.
答案和解析
1.【答案】C
【解答】
AB.合运动的速度(合速度)与分运动的速度(分速度)之间的关系遵循平行四边形定则,其中合速度为平行四边形的对角线,而两个分速度为平行四边形的两个邻边,由几何知识可知,AB错误;
C.合运动指的就是物体的实际运动,.合运动的速度方向就是物体实际运动的方向,故C正确;
D.合运动和分运动具有等时性,故D错误。
故选C。
2.【答案】C
【解答】
小船刚好避开危险区域时,小船合运动方向与水流方向的夹角设为θ,如图所示:
则tan?θ=1001003=33,则θ=30°,当船头垂直合运动方向渡河时,小船在静水中的速度最小,在静水中的最小速度vmin=v水sin?30°=2?m/s,故C正确,ABD错误。
故选C。
3.【答案】C
【解答】
AD、如图
由几何关系可知,开始时河面上的绳长为?sin30?=40m;此时船离岸的距离x1=203m;5s后,绳子向左移动了vt=15m,则河面上绳长为40m?15m=25m;则此时,小船离河边的距离为:x2=252?202m=15m,5s时绳与水面的夹角为α,则有:tanα=2015,解得:α=53°,故AD错误;
B、5s时刻小船前进的距离为:x=203m?15m=19.6m,故B错误;
C、船的速度为合速度,由绳收缩的速度及绳摆动的速度合成得出,则由几何关系可知,cosα=35,则船速v船=vcosα=5m/s,故C正确;
故选:C。
4.【答案】C
【解析】解:A、将小船的运动分解为平行于河岸和垂直于河岸两个方向,抓住分运动和合运动具有等时性,知甲乙两船到达对岸的时间相等.
即渡河的时间t=dvsinθ,故A正确;
B、若仅是河水流速v0增大,渡河的时间t=dvsinθ,则两船的渡河时间都不变,故B正确;
C、只有甲船速度大于水流速度时,不论水流速v0如何改变,甲船都可能到达河的正对岸A点,故C错误;
D、若仅是河水流速v0增大,则两船到达对岸时间不变,根据速度的分解,船在水平方向的分速度的差值仍然不变,则两船之间的距离仍然为l.故D正确.
5.【答案】B
【解答】
AB.根据速度的分解可以求出绳子上的速率为:v1=vcosθ2,所以P的速率等于绳子的速率,故B正确;A错误。
CD.由于v不变,在小车向右匀速运动的过程中,θ2减小,过v1在增大,故P做加速运动,对P进行受力分析得出,绳子上的拉力大于mgsinθ1,故CD错误。
故选B
6.【答案】B
【解答】
AB.物体在0~3s内,x轴方向做匀速直线运动,y轴方向做匀加速直线运动,所以合初速度与加速度不共线,物体的轨迹为曲线,且加速度恒定,所以是匀变速曲线运动,故A错误;B正确;
CD.物体在3~4s内两个方向的分运动都是匀减速运动,在3s末,合速度v与水平方向夹角为37°,ax=?4m/s2,ay=?3m/s2,合加速度方向与水平方向成37°角且与速度方向相反,则做匀减速直线运动,故CD错误。
故选B。
7.【答案】A
【解答】
设小船在静水中的速度为vc;
当船头指向始终与河岸垂直,则有:t去=dvc;
当回程时行驶路线与河岸垂直,则有:t回=dv合
而回头时的船的合速度为:v合=vc2?v2;
由于去程与回程所用时间的比值为k,所以小船在静水中的速度大小为:vc=v21?k2=v1?k2,故A正确,BCD错误。
故选A。?
8.【答案】B
【解析】解:在x方向上有:x=3t2=12axt2,知ax=6m/s2,做初速度为零的匀加速直线运动。在y方向上,有:y=4t2=12ayt2,知ay=8m/s2,做初速度为零的匀加速直线运动。故①正确。
根据平行四边形定则知,a=ax2+ay2=10m/s2,合初速度为零,知合运动做初速度为零,加速度为10m/s2的匀加速直线运动。故③正确。
9.【答案】D
【解答】
飞机的速度的方向:tanα=?vyvx??=?6?60?=?1?10,飞机的加速度的方向:tanβ=?ay?ax?=?0.22??=?1?10,可知飞机的速度的方向与加速度的方向是相同的,飞机做匀变速直线运动。
A.飞机的速度的方向与加速度的方向是相同的,飞机做匀变速直线运动。故A错误;
B.飞机做匀变速直线运动,水平方向的分初速度与竖直方向的分初速度不相等,20s时水平方向的分速度与竖直方向的分速度大小不可能相等。故B错误;
C.飞机做匀变速直线运动,水平方向的分初速度与竖直方向的分初速度不相等,所以在前20s内飞机在水平方向的分位移与竖直方向的分位移大小不可能相等。故C错误;
D.在水平方向上,飞机在20s时的水平速度vx=vx0?at=60m/s?2×20m/s=20m/s,平均速度
vx?=?12?(v0x+vx)=12?(60+20)m/s=40m/s,故D正确。
故选D。
10.【答案】A
【解答】
根据在某段时间内A、B之间距离以l=H?t2的规律变化可以知道H?l=t2,说明伤员在竖直方向上匀加速上升,拉力大于重力,在水平方向上匀速运动,在水平方向一定不受力,合力向上,轨迹弯向所受合力的一侧,故A正确,BCD错误。
11.【答案】C
【解答】
AB.对于A,它的速度如图中标出的vA,这个速度看成是A的合速度,其分速度分别是vavb,其中va就是B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=vAcosθ;
当A环上升至与定滑轮的连线处于水平位置时,va=0,所以B的速度vB=0,故AB错误;
CD.因A匀速上升时,由公式vB=vAcosθ,当A上升时,夹角θ增大,因此B向下做减速运动,由牛顿第二定律,可知绳对B的拉力大于B的重力,B处于超重状态,故C正确,D错误。
故选C。
12.【答案】BD
【解答】
A.根据平行四边形定则,知合速度可能比分速度大,可能比分速度小,可能与分速度相等,故A错误;
B.两个匀速直线运动的合运动一定是匀速直线运动,故 B正确;
C.两个分运动是直线运动,那么合运动也不一定是直线运动,比如平抛运动.故C错误;
D.分运动与合运动具有等时性,故D正确;
故选BD。
13.【答案】AB
【解答】
A.静水速度垂直于河岸,合速度的方向偏向下游,且过河时间最短,A正确;
B.根据平行四边形定则知,合速度的方向正好垂直河岸,过河的位移最小,B正确;
C.由于流水速度,船的合速度会存在偏向下游的分量,因此当船头始终垂直于河岸时,船的航线不可能垂直于河岸,C错误;
D.根据平行四边形定则知,静水速度的方向与流水速度的合速度的方向会偏向下游,船不可能向上游航行,D错误。
故选AB。
14.【答案】AC
【解答】
A.前2s内物体在y轴方向速度为0,由题图知,只沿x方向做匀加速直线运动,故A正确;
D.后2s内物体在x方向做匀速运动,在y方向做初速度为0的匀加速直线运动,加速度沿y轴方向,合运动是曲线运动,故 D错误;
BC.4s内物体在x方向的位移是:x=(12×2×2+2×2)m=6m,在y方向的位移是:y=12×2×2m=2m,所以4s末物体的坐标为(6m,2m),故B错误,C正确。
故选AC。
15.【答案】BD
【解答】
对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vAcosα=vBcosβ,因此vB=cosαcosβvA,α角越来越小,β角越来越大,所以此后B物体的速度越来越大,所以做加速运动,故AC错误,BD正确。
故选BD。
16.【答案】匀速直线? 0.15m/s? 0.25m/s
【解答】
(1)选地面为参考系,红蜡块可以沿管匀速上升,由数据可知,各点的时间间隔相等,那么蜡块的水平方向也是匀速直线运动,依据运动的合成与分解,则蜡块做匀速直线运动;
(2)依据运动学公式,那么蜡块沿玻璃管向上运动的速度大小为:
vy=3×10?12?m/s=0.15?m/s;
(3)依据矢量的合成法则,则蜡块的合速度大小为:
v=vx2+vy2=(4×10?12)2+0.152m/s=0.25m/s。
故答案为:(1)匀速直线;(2)0.15?m/s;(3)0.25?m/s。
17.【答案】(1)等于;(2)A;C
【解答】
(1)由于竖直方向上,操作一和操作二都是匀速运动,且速度相等,竖直方向上运动时间相等,根据合运动和分运动的等时性,两个操作运动时间相等,所以t1等于t2;
(2)操作一中,将速度水平竖直分解,水平方向和竖直方向都是匀速运动,两个方向的分运动的比值始终是定值,所以运动轨迹是一条直线,故选A;
操作二中,红蜡块在水平方向做匀加速直线运动,所以会受到水平向右的恒力,因此运动轨迹会向右偏转,故选C。
故答案为:(1)等于;(2)A;C。
18.【答案】解:(1)小车做匀加速直线运动,由匀变速直线运动的位移公式得:
Htanθ=12at2
解得:a=2Ht2tanθ;
(2)图示时刻小车速度为:v=at=2Ht·tanθ,
将小车B位置的速度沿着平行绳子和垂直绳子方向正交分解,如图所示
根据平行四边形定则,有:v1=vcosθ=2Hcosθt?tanθ,
重物速度:v重=v1=2Hcosθt?tanθ;
19.【答案】?解:(1)小船的实际运动是小船在静水中的运动与船随水漂流运动的合运动,
由于分运动与合运动具有等时性,因此小船渡河时间等于垂直河岸方向分运动的时间,
即
小船沿水流方向的位移s1=v水t1=2×50m=100m
故小船将在50s后到达河对岸下游100m处.
(2)考虑一般情况,设船头与河岸成任意角θ′,如下图所示.
船的过河时间取决于垂直于河岸方向的分速度v⊥,v⊥=v船sinθ′,
故小船过河时间为,当θ′=90°,t2最小,
即船头与河岸垂直时,过河时间最短,最短时间为t2min=50s.
(3)要使小船到达正对岸,船的合速度v应垂直于河岸,
如下图所示,则,故θ=60°.
即船的航向与河岸成60°角,偏向河流上游.
过河时间t=dv=2004sin?60?s=10033s.
(4)因为v′船如下图所示,设船头与河岸成β角,合速度v′与河岸成α角,可以看出α角越大,船沿河岸方向航行的距离x′越小,
那么,在什么条件下α角最大呢?以v′水的矢量末端为圆心,以v′船的大小为半径画圆弧,当合速度v′与圆相切时,α角最大.
cosβ=v′船v′水=35,船头与河岸的夹角β=53°.又x′d=v′v′船=v水′2?v船′2v′船,代入数据解得x′=267m.
即船头与河岸成53°角,偏向上游时,沿河岸方向航行的距离最小,为267 m,
答案:(1)小船在50s后到达对岸下游100 m处.
(2)船头与河岸垂直时,过河时间最短,最短时间为50s.
(3)船头与河岸上游成60°角,历时10033s.
(4)船头与河岸上游成53°角,最小距离是267 m.
20.【答案】解:根据图象可知,物体在x轴方向上以3m/s的速度做匀速直线运动,在y方向上做初速度为零,加速度为0.5m/s2的匀加速直线运动,合运动是曲线运动.
(1)由图看出,t=0时x轴方向分速度为vx=3m/s,y轴方向分速度为vy=,故t=0时物体的速度为v0=vx=3m/s;
(2)在t=8s时刻,vx=3m/s,vy=4m/s,所以物体的速度v=vx2+vy2=5m/s;
(3)根据v?t图象中图象与时间轴围成的面积表示位移,则知在4s的时间内,x轴方向的分位移为x=3×4m=12m,y=12×2×4m=4m,
所以4s内物体发生的位移为s=x2+y2=410m。
一、单选题
对于两个分运动及其合运动,下列说法正确的是(????)
A. 合运动的速度一定比两个分运动的速度都大
B. 合运动的速度至少比其中一个分运动的速度大
C. 合运动的速度方向就是物体实际运动的方向
D. 合运动的时间一定比分运动的时间长
如图所示,一条小船位于200?m宽的河中央A点处,离A点距离为1003m的下游处有一危险的急流区,当时水流速度为4?m/s,为使小船避开危险区沿直线到达对岸,小船在静止水中的速度至少为(????)
A. 433m/s B. 833m/s C. 2?m/s D. 4?m/s
如下图所示,有人在河面上方20m的岸上用跨过定滑轮的长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率ν=3m/s拉绳使小船靠岸,那么(??? )
A. 5s时绳与水面的夹角为60° B. 5s时小船前进了15m
C. 5s时小船的速率为5m/s D. 5s时小船到岸边距离为10m
甲、乙两船在同一河流中同时开始渡河,河水流速为v0。两船在静水中的速率均为,甲、乙两船船头均与河岸夹角为,如图所示,已知甲船恰好能垂直到达河正对岸的点,乙船到达河对岸的点,A,B之间的距离为。则下列判断错误的是(??? )
A. 甲、乙两船同时到达对岸
B. 若仅是河水流速v0增大,则两船的渡河时间都不变
C. 不论河水流速v0如何改变,只要适当改变角,甲船总能到达正对岸的点
D. 若仅是河水流速v0增大,则两船到达对岸时,两船之间的距离仍然为
质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动当小车与滑轮间的细绳和水平方向成夹角θ2时(如图),下列判断正确的是(? ? ? ?).
A. P的速率为v B. P的速率为vcosθ2
C. 绳的拉力等于mgsinθ1 D. 绳的拉力小于mgsinθ1
物体在直角坐标系xOy所在平面内由O点开始运动,其沿坐标轴方向的两个分速度随时间变化的图象如图所示,则对该物体运动过程的描述正确的是(????)
A. 物体在0~3?s做匀变速直线运动 B. 物体在0~3?s做匀变速曲线运动
C. 物体在3~4?s做变加速直线运动 D. 物体在3~4?s做匀变速曲线运动
有一条两岸平直、河水均匀流动、流速恒为v的大河。小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直。去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为(????)
A. v1?k2 B. kvk2?1 C. kv1?k2 D. vk2?1
直角坐标系xOy在水平面内,一物体的运动规律是x=3t2m;y=4t2m(t的单位为s),则下列说法中正确的是(??? )
①物体在x和y方向上都是做初速度为零的匀加速运动
②物体的合运动是初速度为零、加速度为5m/s2的匀加速直线运动
③物体的合运动是初速度为零、加速度为10m/s2的匀加速直线运动
④物体的合运动是加速度为5m/s2的曲线运动
A. ①② B. ①③ C. ②③ D. ②④
在第十一届珠海国际航展上,歼?20战机是此次航展最大的“明星”.如图所示,歼?20战机在降落过程中水平方向的初速度为60m/s,竖直方向的初速度为6m/s,已知歼?20战机在水平方向做加速度大小为2m/s2的匀减速直线运动,在竖直方向做加速度大小为0.2m/s2的匀减速直线运动,则歼?20战机在降落过程中,下列说法正确的是(??? )
A. 歼?20战机的运动轨迹为曲线
B. 经20s,歼?20战机水平方向的分速度与竖直方向的分速度大小相等
C. 在前20s内,歼?20战机在水平方向的分位移与竖直方向的分位移大小相等
D. 歼?20战机在前20s内,水平方向的平均速度为40m/s
如图所示,在一次救灾工作中,一架离水面高为H、沿水平直线飞行的直升机A,用悬索(重力可忽略不计)救护困在湖水中的伤员B,在直升机A和伤员B以相同的水平速率匀速运动的同时,悬索将伤员吊起.设经t时间后,A,B之间的距离为l,且l=H?t2,则在这段时间内伤员B的受力情况和运动轨迹是哪个图(??? )
A. B. C. D.
如下图所示,套在竖直固定细杆上的环A由跨过定滑轮且不可伸长的轻绳与B相连,在外力作用下A沿杆以速度νA匀速上升经过P、Q两点,经过P点时绳与竖直杆间的夹角为α,经过Q点时A与定滑轮的连线处于水平方向,则下列说法正确的是(??? )
A. 经过P点时,B的速度等于νAcosα
B. 经过Q点时,B的速度方向向下
C. 当A从P至Q的过程中,B处超重状态
D. 当A从P至Q的过程中,绳的拉力等于B的重力
二、多选题
关于运动的合成,下列说法中正确的是(????)
A. 合运动速度一定比每一个分运动速度大
B. 两个匀速直线运动的合运动一定是匀速直线运动
C. 只要两个分运动是直线运动,那么它们的合运动也一定是直线运动
D. 两个分运动的时间一定与它们的合运动的时间相等
下列图中实线为河岸,河水的流动方向如图v的箭头所示,虚线为小船从河岸M驶向对岸N的实际航线。则其中可能正确的是(????)
A. B.
C. D.
在一光滑水平面内建立平面直角坐标系xoy,一物体从t=0时刻起,由坐标原点O(0,0)开始运动,其沿x轴和y轴方向运动的速度时间图象如图所示,下列说法中正确的是(????)
A. 前2?s内物体沿x轴做匀加速直线运动
B. 4?s末物体坐标为(4m,4?m)
C. 4?s末物体坐标为(6?m,2m)
D. 后2?s内物体继续做匀加速直线运动,但加速度沿y轴方向
(多选)一根细绳通过定滑轮且两端分别系着A和B两物体,如下图所示,物体A在外力作用下,向左以νA匀速运动,当连A的绳子与水平方向成α角,连B的绳子与水平方向成β角时,B物体的速度为νB,则(??? )
A. A物体的速度νA与B物体的速度νB的大小相等
B. A物体的速度νA与B物体的速度νB的大小关系满足νBcosβ=νAcosα
C. 此后B物体以速度νB做匀速运动
D. 此后B物体的速度越来越大,所以做加速运动
三、实验题
如图1所示的是研究运动的合成与分解的实验装置,长约1.5m可密封的玻璃管内径均匀,里面充满水,在水中放置一个红色的蜡块,仔细调整蜡块的大小,使蜡块与管内壁间的间隙大小合适,当玻璃管相对于地面静止竖直放置时,红蜡块可以沿管匀速上升。实验时,保持管的底端在同一水平面,管子始终保持竖直。当蜡块开始向上匀速运动时,使管子整体沿水平方向运动,每隔2s记录下蜡块所在的位置(选地面为参考系),如图2所示。则由图中所记录的数据,可以得到:
(1)选地面为参考系,蜡块做_____ 运动;
(2)蜡块沿管子向上运动的速度是_____;
(3)蜡块合速度大小为_____。
如图甲所示,实验小组在竖直放置的两端封闭的玻璃管中注满清水,内有一个圆柱形的红蜡块能从坐标圆点O在水中匀速上浮。现进行如下操作:
??? 操作一:当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平向右匀速运动,测得红蜡块运动到顶端所需时间为t1。
??? 操作二:当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管从静止水平向右做匀加速直线运动,测得红蜡块从下端运动到顶端所需时间为t2。
根据以上信息,回答下列问题:
(1)t1________t2(选填“大于”、“小于”或“等于”);
(2)在图乙中,能正确反映操作一中红蜡块上升过程中运动轨迹的示意图是________;能正确反映操作二中红蜡块上升过程中运动轨迹的示意图是________。
四、计算题
一辆车通过一根跨过光滑轻质定滑轮的轻绳提升一个质量为m的重物,开始车在滑轮的正下方,绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速直线运动,经过时间t绳子与水平方向的夹角为θ,如图所示.试求:
?
(1)车向左运动的加速度的大小;
(2)重物m在t时刻速度的大小.
小船在200m宽的河中航行,水流速度为2m/s,船在静水中的速度为4m/s.已知cos53°=35.
(1)若小船在河中垂直于河岸航行,小船将在何时、何处到达对岸?
(2)小船怎样过河用时最短?过河的最短时间为多少?
(3)要使小船到达正对岸,应如何航行?历时多久?
(4)若水流速度是5m/s,船在静水中的速度是3m/s,则怎样过河才能使船沿河岸方向航行的距离最小?该最小距离是多少?
如下图所示,甲图表示某物体在x轴上分速度的νx?t图像,乙图表示该物体在y轴方向上分速度的νy?t图像.求:
? ? ? ? ? ?
? ? ? ? ?甲? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?乙
(1)在t=0时刻物体的速度大小;
(2)在t=8s时刻物体的速度大小;
(3)在0~4s内物体的位移大小.
答案和解析
1.【答案】C
【解答】
AB.合运动的速度(合速度)与分运动的速度(分速度)之间的关系遵循平行四边形定则,其中合速度为平行四边形的对角线,而两个分速度为平行四边形的两个邻边,由几何知识可知,AB错误;
C.合运动指的就是物体的实际运动,.合运动的速度方向就是物体实际运动的方向,故C正确;
D.合运动和分运动具有等时性,故D错误。
故选C。
2.【答案】C
【解答】
小船刚好避开危险区域时,小船合运动方向与水流方向的夹角设为θ,如图所示:
则tan?θ=1001003=33,则θ=30°,当船头垂直合运动方向渡河时,小船在静水中的速度最小,在静水中的最小速度vmin=v水sin?30°=2?m/s,故C正确,ABD错误。
故选C。
3.【答案】C
【解答】
AD、如图
由几何关系可知,开始时河面上的绳长为?sin30?=40m;此时船离岸的距离x1=203m;5s后,绳子向左移动了vt=15m,则河面上绳长为40m?15m=25m;则此时,小船离河边的距离为:x2=252?202m=15m,5s时绳与水面的夹角为α,则有:tanα=2015,解得:α=53°,故AD错误;
B、5s时刻小船前进的距离为:x=203m?15m=19.6m,故B错误;
C、船的速度为合速度,由绳收缩的速度及绳摆动的速度合成得出,则由几何关系可知,cosα=35,则船速v船=vcosα=5m/s,故C正确;
故选:C。
4.【答案】C
【解析】解:A、将小船的运动分解为平行于河岸和垂直于河岸两个方向,抓住分运动和合运动具有等时性,知甲乙两船到达对岸的时间相等.
即渡河的时间t=dvsinθ,故A正确;
B、若仅是河水流速v0增大,渡河的时间t=dvsinθ,则两船的渡河时间都不变,故B正确;
C、只有甲船速度大于水流速度时,不论水流速v0如何改变,甲船都可能到达河的正对岸A点,故C错误;
D、若仅是河水流速v0增大,则两船到达对岸时间不变,根据速度的分解,船在水平方向的分速度的差值仍然不变,则两船之间的距离仍然为l.故D正确.
5.【答案】B
【解答】
AB.根据速度的分解可以求出绳子上的速率为:v1=vcosθ2,所以P的速率等于绳子的速率,故B正确;A错误。
CD.由于v不变,在小车向右匀速运动的过程中,θ2减小,过v1在增大,故P做加速运动,对P进行受力分析得出,绳子上的拉力大于mgsinθ1,故CD错误。
故选B
6.【答案】B
【解答】
AB.物体在0~3s内,x轴方向做匀速直线运动,y轴方向做匀加速直线运动,所以合初速度与加速度不共线,物体的轨迹为曲线,且加速度恒定,所以是匀变速曲线运动,故A错误;B正确;
CD.物体在3~4s内两个方向的分运动都是匀减速运动,在3s末,合速度v与水平方向夹角为37°,ax=?4m/s2,ay=?3m/s2,合加速度方向与水平方向成37°角且与速度方向相反,则做匀减速直线运动,故CD错误。
故选B。
7.【答案】A
【解答】
设小船在静水中的速度为vc;
当船头指向始终与河岸垂直,则有:t去=dvc;
当回程时行驶路线与河岸垂直,则有:t回=dv合
而回头时的船的合速度为:v合=vc2?v2;
由于去程与回程所用时间的比值为k,所以小船在静水中的速度大小为:vc=v21?k2=v1?k2,故A正确,BCD错误。
故选A。?
8.【答案】B
【解析】解:在x方向上有:x=3t2=12axt2,知ax=6m/s2,做初速度为零的匀加速直线运动。在y方向上,有:y=4t2=12ayt2,知ay=8m/s2,做初速度为零的匀加速直线运动。故①正确。
根据平行四边形定则知,a=ax2+ay2=10m/s2,合初速度为零,知合运动做初速度为零,加速度为10m/s2的匀加速直线运动。故③正确。
9.【答案】D
【解答】
飞机的速度的方向:tanα=?vyvx??=?6?60?=?1?10,飞机的加速度的方向:tanβ=?ay?ax?=?0.22??=?1?10,可知飞机的速度的方向与加速度的方向是相同的,飞机做匀变速直线运动。
A.飞机的速度的方向与加速度的方向是相同的,飞机做匀变速直线运动。故A错误;
B.飞机做匀变速直线运动,水平方向的分初速度与竖直方向的分初速度不相等,20s时水平方向的分速度与竖直方向的分速度大小不可能相等。故B错误;
C.飞机做匀变速直线运动,水平方向的分初速度与竖直方向的分初速度不相等,所以在前20s内飞机在水平方向的分位移与竖直方向的分位移大小不可能相等。故C错误;
D.在水平方向上,飞机在20s时的水平速度vx=vx0?at=60m/s?2×20m/s=20m/s,平均速度
vx?=?12?(v0x+vx)=12?(60+20)m/s=40m/s,故D正确。
故选D。
10.【答案】A
【解答】
根据在某段时间内A、B之间距离以l=H?t2的规律变化可以知道H?l=t2,说明伤员在竖直方向上匀加速上升,拉力大于重力,在水平方向上匀速运动,在水平方向一定不受力,合力向上,轨迹弯向所受合力的一侧,故A正确,BCD错误。
11.【答案】C
【解答】
AB.对于A,它的速度如图中标出的vA,这个速度看成是A的合速度,其分速度分别是vavb,其中va就是B的速度vB(同一根绳子,大小相同),刚开始时B的速度为vB=vAcosθ;
当A环上升至与定滑轮的连线处于水平位置时,va=0,所以B的速度vB=0,故AB错误;
CD.因A匀速上升时,由公式vB=vAcosθ,当A上升时,夹角θ增大,因此B向下做减速运动,由牛顿第二定律,可知绳对B的拉力大于B的重力,B处于超重状态,故C正确,D错误。
故选C。
12.【答案】BD
【解答】
A.根据平行四边形定则,知合速度可能比分速度大,可能比分速度小,可能与分速度相等,故A错误;
B.两个匀速直线运动的合运动一定是匀速直线运动,故 B正确;
C.两个分运动是直线运动,那么合运动也不一定是直线运动,比如平抛运动.故C错误;
D.分运动与合运动具有等时性,故D正确;
故选BD。
13.【答案】AB
【解答】
A.静水速度垂直于河岸,合速度的方向偏向下游,且过河时间最短,A正确;
B.根据平行四边形定则知,合速度的方向正好垂直河岸,过河的位移最小,B正确;
C.由于流水速度,船的合速度会存在偏向下游的分量,因此当船头始终垂直于河岸时,船的航线不可能垂直于河岸,C错误;
D.根据平行四边形定则知,静水速度的方向与流水速度的合速度的方向会偏向下游,船不可能向上游航行,D错误。
故选AB。
14.【答案】AC
【解答】
A.前2s内物体在y轴方向速度为0,由题图知,只沿x方向做匀加速直线运动,故A正确;
D.后2s内物体在x方向做匀速运动,在y方向做初速度为0的匀加速直线运动,加速度沿y轴方向,合运动是曲线运动,故 D错误;
BC.4s内物体在x方向的位移是:x=(12×2×2+2×2)m=6m,在y方向的位移是:y=12×2×2m=2m,所以4s末物体的坐标为(6m,2m),故B错误,C正确。
故选AC。
15.【答案】BD
【解答】
对A物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vAcosα;对B物体的速度沿着绳子方向与垂直绳子方向进行分解,则有沿着绳子方向的速度大小为vBcosβ,由于沿着绳子方向速度大小相等,所以则有vAcosα=vBcosβ,因此vB=cosαcosβvA,α角越来越小,β角越来越大,所以此后B物体的速度越来越大,所以做加速运动,故AC错误,BD正确。
故选BD。
16.【答案】匀速直线? 0.15m/s? 0.25m/s
【解答】
(1)选地面为参考系,红蜡块可以沿管匀速上升,由数据可知,各点的时间间隔相等,那么蜡块的水平方向也是匀速直线运动,依据运动的合成与分解,则蜡块做匀速直线运动;
(2)依据运动学公式,那么蜡块沿玻璃管向上运动的速度大小为:
vy=3×10?12?m/s=0.15?m/s;
(3)依据矢量的合成法则,则蜡块的合速度大小为:
v=vx2+vy2=(4×10?12)2+0.152m/s=0.25m/s。
故答案为:(1)匀速直线;(2)0.15?m/s;(3)0.25?m/s。
17.【答案】(1)等于;(2)A;C
【解答】
(1)由于竖直方向上,操作一和操作二都是匀速运动,且速度相等,竖直方向上运动时间相等,根据合运动和分运动的等时性,两个操作运动时间相等,所以t1等于t2;
(2)操作一中,将速度水平竖直分解,水平方向和竖直方向都是匀速运动,两个方向的分运动的比值始终是定值,所以运动轨迹是一条直线,故选A;
操作二中,红蜡块在水平方向做匀加速直线运动,所以会受到水平向右的恒力,因此运动轨迹会向右偏转,故选C。
故答案为:(1)等于;(2)A;C。
18.【答案】解:(1)小车做匀加速直线运动,由匀变速直线运动的位移公式得:
Htanθ=12at2
解得:a=2Ht2tanθ;
(2)图示时刻小车速度为:v=at=2Ht·tanθ,
将小车B位置的速度沿着平行绳子和垂直绳子方向正交分解,如图所示
根据平行四边形定则,有:v1=vcosθ=2Hcosθt?tanθ,
重物速度:v重=v1=2Hcosθt?tanθ;
19.【答案】?解:(1)小船的实际运动是小船在静水中的运动与船随水漂流运动的合运动,
由于分运动与合运动具有等时性,因此小船渡河时间等于垂直河岸方向分运动的时间,
即
小船沿水流方向的位移s1=v水t1=2×50m=100m
故小船将在50s后到达河对岸下游100m处.
(2)考虑一般情况,设船头与河岸成任意角θ′,如下图所示.
船的过河时间取决于垂直于河岸方向的分速度v⊥,v⊥=v船sinθ′,
故小船过河时间为,当θ′=90°,t2最小,
即船头与河岸垂直时,过河时间最短,最短时间为t2min=50s.
(3)要使小船到达正对岸,船的合速度v应垂直于河岸,
如下图所示,则,故θ=60°.
即船的航向与河岸成60°角,偏向河流上游.
过河时间t=dv=2004sin?60?s=10033s.
(4)因为v′船
那么,在什么条件下α角最大呢?以v′水的矢量末端为圆心,以v′船的大小为半径画圆弧,当合速度v′与圆相切时,α角最大.
cosβ=v′船v′水=35,船头与河岸的夹角β=53°.又x′d=v′v′船=v水′2?v船′2v′船,代入数据解得x′=267m.
即船头与河岸成53°角,偏向上游时,沿河岸方向航行的距离最小,为267 m,
答案:(1)小船在50s后到达对岸下游100 m处.
(2)船头与河岸垂直时,过河时间最短,最短时间为50s.
(3)船头与河岸上游成60°角,历时10033s.
(4)船头与河岸上游成53°角,最小距离是267 m.
20.【答案】解:根据图象可知,物体在x轴方向上以3m/s的速度做匀速直线运动,在y方向上做初速度为零,加速度为0.5m/s2的匀加速直线运动,合运动是曲线运动.
(1)由图看出,t=0时x轴方向分速度为vx=3m/s,y轴方向分速度为vy=,故t=0时物体的速度为v0=vx=3m/s;
(2)在t=8s时刻,vx=3m/s,vy=4m/s,所以物体的速度v=vx2+vy2=5m/s;
(3)根据v?t图象中图象与时间轴围成的面积表示位移,则知在4s的时间内,x轴方向的分位移为x=3×4m=12m,y=12×2×4m=4m,
所以4s内物体发生的位移为s=x2+y2=410m。
