人教版八年级数学:第十八章《平行四边形》相关计算与证明解答题提升专练(word版,无答案)
文档属性
| 名称 | 人教版八年级数学:第十八章《平行四边形》相关计算与证明解答题提升专练(word版,无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览


文档简介
八年级数学四边形的相关计算与证明解答题提升专练
题型一:判定图形的形状
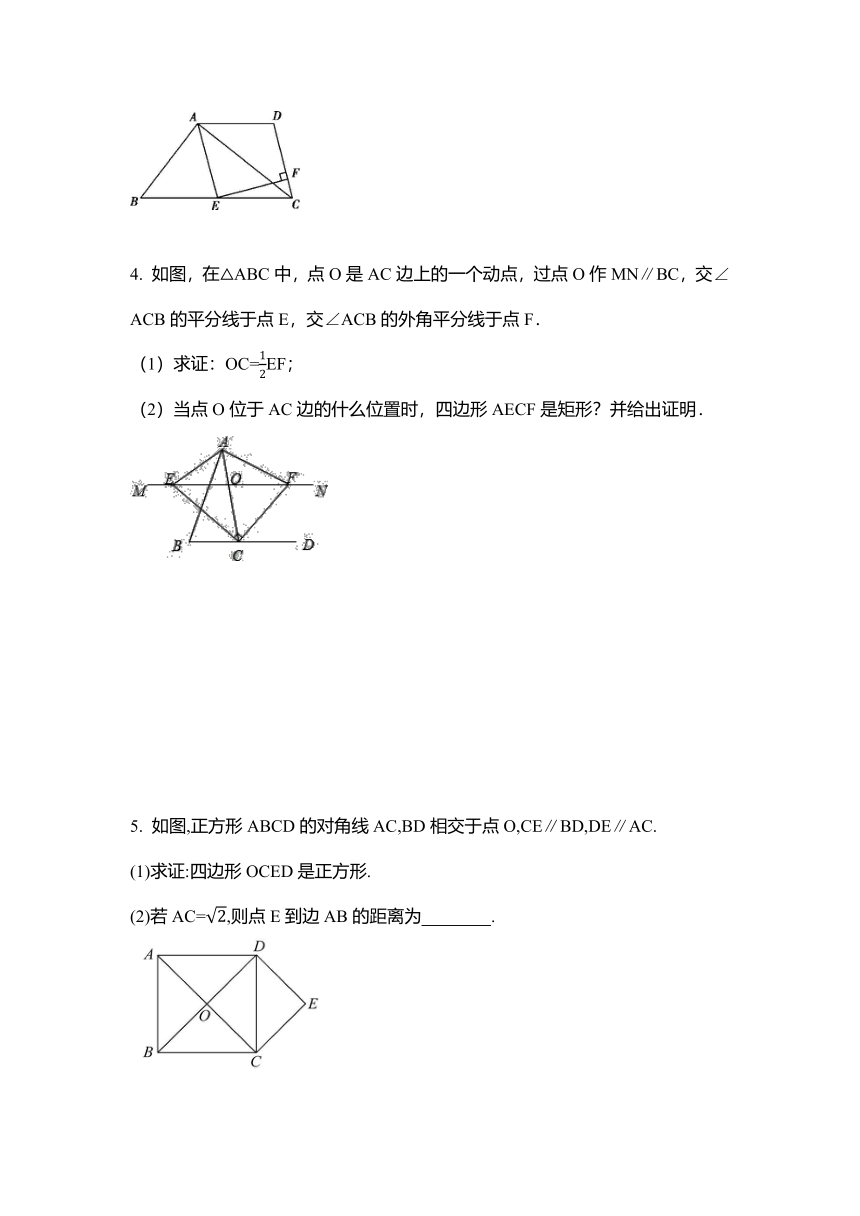
1.如图,四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE.求证:四边形AEFD是平行四边形.
2. 如图,∠B=∠E=90°,点B、C、F、E在一条直线上,AC=DF,BF=EC.求证:四边形ACDF是平行四边形.
3. 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥
CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.
4. 如图,在△ABC中,点O是AC边上的一个动点,过点O作MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OC=12EF;
(2)当点O位于AC边的什么位置时,四边形AECF是矩形?并给出证明.
5. 如图,正方形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED是正方形.
(2)若AC=2,则点E到边AB的距离为 .?
题型二:长度、面积相关的计算或证明
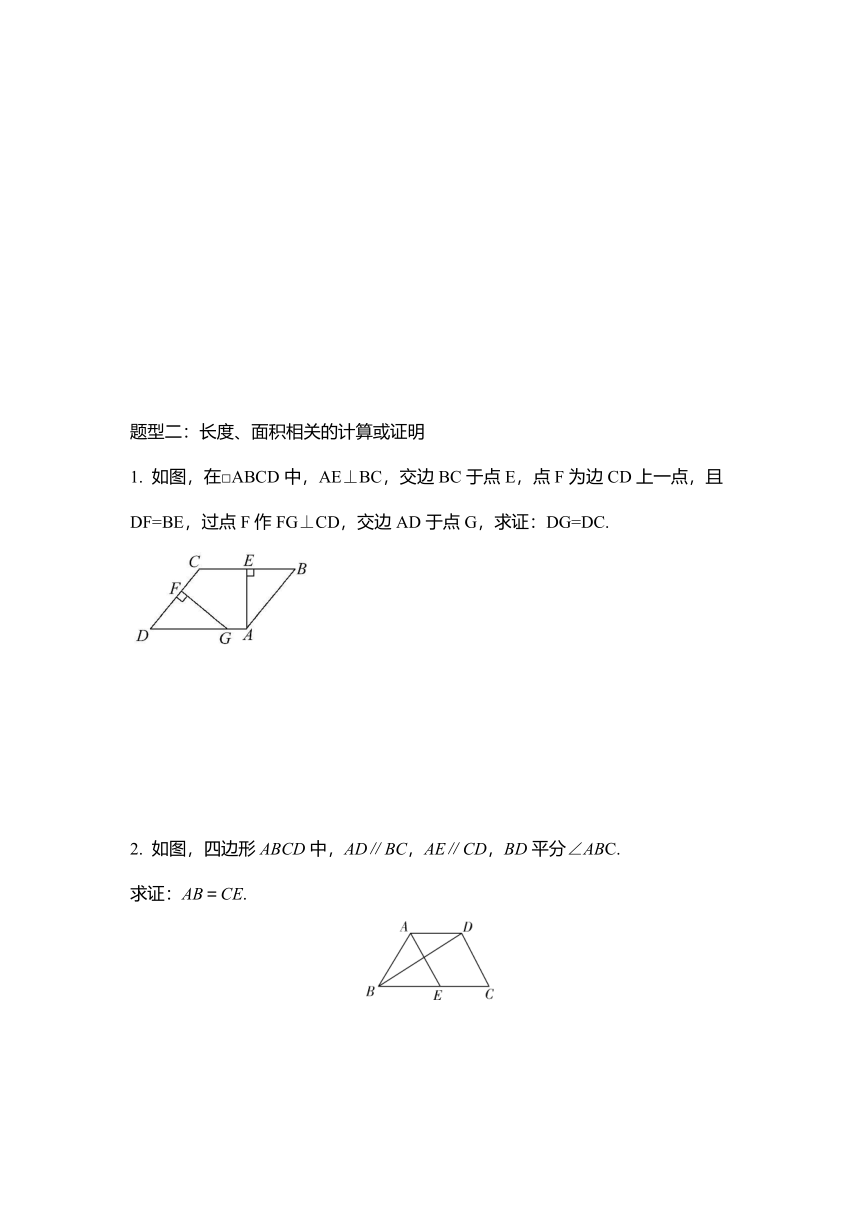
1. 如图,在□ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE,过点F作FG⊥CD,交边AD于点G,求证:DG=DC.
2. 如图,四边形ABCD中,AD∥BC,AE∥CD,BD平分∠ABC.
求证:AB=CE.
3. 如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD、BE,∠ABD=90°.求证:BC=CD.
4. 如图,在平行四边形ABCD中,点O是对角线AC的中点,点E在AD的延长线上,连接EO,并延长交CB的延长线于点F.
求证:DE=BF.
5. 如图,平行四边形 ABCD中,BE⊥AD,BF⊥CD,∠EBF=60°,AE=3,DF=2.求EC、EF的长.
题型三:角度相关的计算或证明
1. 如图,在菱形ABCD中,点E为对角线AC上一点,连接DE并延长交AB延长线于点F,连接BE.求证:∠AFD=∠EBC.
2. 如图,四边形ABCD是矩形,过点D作DE∥AC,交BA的延长线于点E.
求证:∠BDA=∠EDA.
3. 如图,已知在四边形ABCD中,BC=AD,点E、F分别是BC、AD边上的中点,且AE=CF.
求证:AB∥CD.
4.如图,正方形ABCD中,点E、F分别在AD、CD上,且DE=CF,AF、BE相交于点G.求证:BE⊥AF.
题型四:四边形的综合应用
1. 如图,正方形ABCD的边长为6,E、F是对角线BD上的两个动点,且EF=2,连接AE、AF,求AE+AF的最小值.
2. 如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
3.如图,在平行四边形ABCD中,点E是CD的中点,连接AE,F为AE上一点,且∠BFE=∠C.求证:AB2=2AE·AF.
4. 综合与实践
问题情境:
如图①,点为正方形内一点,,将Rt△ABE绕点按顺时针方向旋转,得到△(点的对应点为点.延长交于点,连接.
猜想证明:
(1)试判断四边形的形状,并说明理由;
(2)如图②,若,请猜想线段与的数量关系并加以证明;
解决问题:
(3)如图①,若,,请直接写出的长.
题型一:判定图形的形状
1.如图,四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE.求证:四边形AEFD是平行四边形.
2. 如图,∠B=∠E=90°,点B、C、F、E在一条直线上,AC=DF,BF=EC.求证:四边形ACDF是平行四边形.
3. 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥
CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.
4. 如图,在△ABC中,点O是AC边上的一个动点,过点O作MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OC=12EF;
(2)当点O位于AC边的什么位置时,四边形AECF是矩形?并给出证明.
5. 如图,正方形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED是正方形.
(2)若AC=2,则点E到边AB的距离为 .?
题型二:长度、面积相关的计算或证明
1. 如图,在□ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE,过点F作FG⊥CD,交边AD于点G,求证:DG=DC.
2. 如图,四边形ABCD中,AD∥BC,AE∥CD,BD平分∠ABC.
求证:AB=CE.
3. 如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD、BE,∠ABD=90°.求证:BC=CD.
4. 如图,在平行四边形ABCD中,点O是对角线AC的中点,点E在AD的延长线上,连接EO,并延长交CB的延长线于点F.
求证:DE=BF.
5. 如图,平行四边形 ABCD中,BE⊥AD,BF⊥CD,∠EBF=60°,AE=3,DF=2.求EC、EF的长.
题型三:角度相关的计算或证明
1. 如图,在菱形ABCD中,点E为对角线AC上一点,连接DE并延长交AB延长线于点F,连接BE.求证:∠AFD=∠EBC.
2. 如图,四边形ABCD是矩形,过点D作DE∥AC,交BA的延长线于点E.
求证:∠BDA=∠EDA.
3. 如图,已知在四边形ABCD中,BC=AD,点E、F分别是BC、AD边上的中点,且AE=CF.
求证:AB∥CD.
4.如图,正方形ABCD中,点E、F分别在AD、CD上,且DE=CF,AF、BE相交于点G.求证:BE⊥AF.
题型四:四边形的综合应用
1. 如图,正方形ABCD的边长为6,E、F是对角线BD上的两个动点,且EF=2,连接AE、AF,求AE+AF的最小值.
2. 如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
3.如图,在平行四边形ABCD中,点E是CD的中点,连接AE,F为AE上一点,且∠BFE=∠C.求证:AB2=2AE·AF.
4. 综合与实践
问题情境:
如图①,点为正方形内一点,,将Rt△ABE绕点按顺时针方向旋转,得到△(点的对应点为点.延长交于点,连接.
猜想证明:
(1)试判断四边形的形状,并说明理由;
(2)如图②,若,请猜想线段与的数量关系并加以证明;
解决问题:
(3)如图①,若,,请直接写出的长.
