6.3 向心加速度同步练习(word版含答案)
文档属性
| 名称 | 6.3 向心加速度同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 242.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-15 22:43:03 | ||
图片预览




文档简介
向心加速度练习
一、单选题
A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4:3,运动方向改变的角度之比是3:2,则它们的(????)
A. 线速度大小之比为4:3 B. 角速度之比为3:4
C. 圆周运动半径之比为2:1 D. 向心加速度大小之比为1:2
关于向心加速度,下列说法正确的是(????)
A. 由an=ν2r知,匀速圆周运动的向心加速度恒定
B. 做圆周运动的物体,加速度时刻指向圆心
C. 向心加速度越大,物体速率变化越快
D. 匀速圆周运动不属于匀速运动
甲、乙两个物体都做匀速圆周运动,转动半径之比为9:4,转动的周期之比为3:4,则它们所受的向心加速度之比为(????)
A. 1:4 B. 4:1 C. 4:9 D. 9:4
如下图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB∶RC=3∶2.A轮的半径与C轮相同,它与B轮紧靠在一起.当A轮绕其中心的竖直轴转动时,由于摩擦作用,B轮也会随之无滑动地转动.a、b、c分别为三个转轮A、B、C边缘上的三个点,在运动过程中,a、b、c三点的(??? )
A. 线速度大小之比为3∶2∶2 B. 角速度大小之比为3∶3∶2
C. 转速之比为2∶3∶2 D. 向心加速度大小之比为9∶6∶4
如下图所示,半径为R的圆环竖直放置,一轻弹簧一端固定在环的最高点A,另一端系一带有小孔穿在环上的小球,弹簧原长为23R将小球从静止开始释放,释放时弹簧恰无形变,小球运动到环的最低点时速率为ν,这时小球向心加速度的大小为(??? )
A. ν2R
B. ν22R
C. 3ν22R
D. 3ν24R
如图所示,A、B为啮合传动的两齿轮,RA=2RB,则A、B两轮边缘上两点的(????)
A. 角速度之比为2∶1 B. 向心加速度之比为1∶2
C. 周期之比为1∶2 D. 转速之比为2∶1
如图所示是自行车的轮盘与车轴上的飞轮之间的链条传动装置.P是轮盘的一个齿,Q是飞轮上的一个齿.下列说法中正确的是(????)
A. P、Q两点角速度大小相等
B. P、Q两点线速度大小相等
C. P、Q两点向心加速度大小相等
D. P点向心加速度大于Q点向心加速度
假设宇宙中有两颗相距无限远的行星A和B,半径分别为RA和RB两颗行星周围卫星的轨道半径的三次方(r3)与运行周期的平方(T2)的关系如图所示,T0为卫星环绕行星表面运行的周期。则(??? )
A. 行星A的质量小于行星B的质量
B. 行星A的密度小于行星B的密度
C. 行星A的第一宇宙速度等于行星B的第一宇宙速度
D. 当两行星的卫星轨道半径相同时,行星A的卫星向心加速度大于行星B的卫星向心加速度
如下图所示,公园的“魔法旋转圆盘”绕过圆心的竖直轴在水平面内匀速转动,一小孩站在圆盘上某处的P点(非圆心)相对圆盘静止.下列说法正确的是(????)
A. 小孩在P点相对圆盘静止,因此他不受摩擦力作用
B. 若使圆盘以较小的转速(不为零)转动,则小孩在P点受到的摩擦力为零
C. 若小孩随圆盘一起做变速圆周运动,则其所受摩擦力方向不指向圆心
D. 若小孩在距离圆心更近的另一点相对圆盘静止且圆盘转速不变,则小孩受到的摩擦力增大
如图所示,两个质量相同的小球用长度不等的不可伸长的细线拴在同一点,并在同一水平面内做同方向的匀速圆周运动,则它们的(????)
A. 向心力大小相同
B. 运动周期不同
C. 运动线速度大小相同
D. 运动角速度相同
如图所示,一小物块以大小为4?m/s2的向心加速度做匀速圆周运动,半径R=1?m,则下列说法正确的是(??? )
A. 小物块做圆周运动的周期为1?s
B. 小物块运动的角速度为2?rad/s
C. 小物块在π?s内通过的路程为零
D. 小物块在t=π4s内通过的位移大小为π20m
如图所示,一个传动装置中有三个紧挨着的摩擦轮A、B和C,B为主动轮,A和C均为从动轮,它们的半径分别为:rA=8cm,rB=6cm,rC=4cm,则两个从动轮在主动轮的带动下不打滑转动时,A、C两个从动轮边缘上的质点(????)
A. 线速度之比vA:vC=2:1
B. 角速度之比为ωA:ωC=2:1
C. 周期之比为TA:TC=2:1
D. 向心加速度之比为aA:aC=2:1
二、多选题
(多选)某实验楼大厅里科普器材中有如下图所示的传动装置:在大齿轮盘内嵌有三个等大的小齿轮.若齿轮的齿很小,大齿轮半径(内径)是小齿轮半径的3倍,则当大齿轮顺时针匀速转动时,下列说法正确的是(????)
A. 小齿轮逆时针匀速转动
B. 小齿轮的每个齿的线速度均相同
C. 小齿轮的角速度是大齿轮角速度的3倍
D. 小齿轮每个齿的向心加速度是大齿轮每个齿的向心加速度的3倍
如图所示,A、B、C三个物体放在旋转平台上随平台一起做匀速圆周运动,动摩擦因数均为μ,已知A的质量为3m,B、C的质量均为m,A、B离轴距离均为R,C距离轴为2R,则以下说法正确的是(????)
A. aA=aC>aB B. aA=aBfC>fB? D. fA>fB>fC
如图所示,长为L的细绳一端固定在O点,另一端拴住一个小球,在O点的正下方与O点相距L2的地方有一枚与竖直平面垂直的钉子,把球拉起使细绳在水平方向伸直,由静止开始释放,当细绳碰到钉子的瞬间,下列说法正确的是(????)
A. 小球的角速度突然增大 B. 小球的线速度突然增大
C. 小球的向心加速度突然增大 D. 小球的向心加速度不变
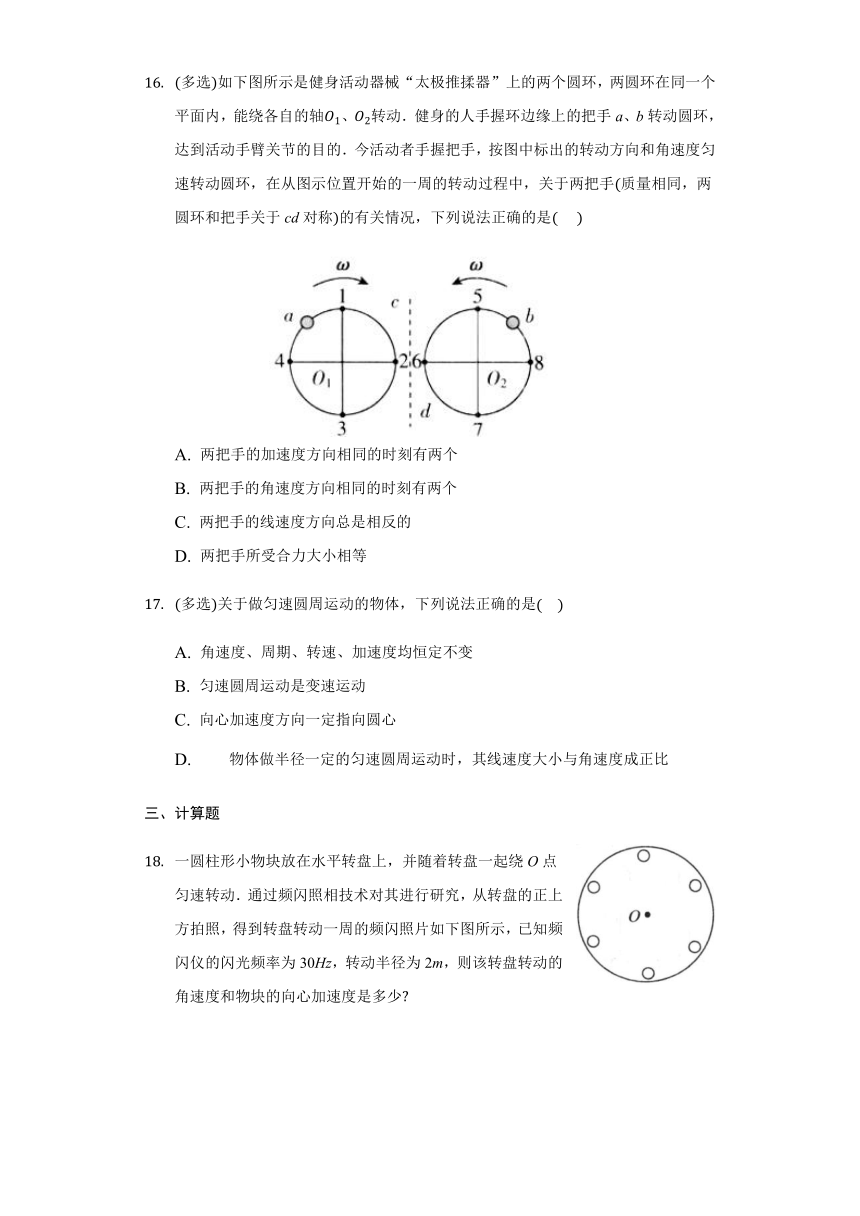
(多选)如下图所示是健身活动器械“太极推揉器”上的两个圆环,两圆环在同一个平面内,能绕各自的轴O1、O2转动.健身的人手握环边缘上的把手a、b转动圆环,达到活动手臂关节的目的.今活动者手握把手,按图中标出的转动方向和角速度匀速转动圆环,在从图示位置开始的一周的转动过程中,关于两把手(质量相同,两圆环和把手关于cd对称)的有关情况,下列说法正确的是(??? )
A. 两把手的加速度方向相同的时刻有两个
B. 两把手的角速度方向相同的时刻有两个
C. 两把手的线速度方向总是相反的
D. 两把手所受合力大小相等
(多选)关于做匀速圆周运动的物体,下列说法正确的是(????)
A. 角速度、周期、转速、加速度均恒定不变
B. 匀速圆周运动是变速运动
C. 向心加速度方向一定指向圆心
D. 物体做半径一定的匀速圆周运动时,其线速度大小与角速度成正比
三、计算题
一圆柱形小物块放在水平转盘上,并随着转盘一起绕O点匀速转动.通过频闪照相技术对其进行研究,从转盘的正上方拍照,得到转盘转动一周的频闪照片如下图所示,已知频闪仪的闪光频率为30Hz,转动半径为2m,则该转盘转动的角速度和物块的向心加速度是多少?
如下图所示,某滑板运动员恰好从B点进入半径为2m的14圆弧轨道,该圆弧轨道在C点与水平轨道相接,运动员滑到C点时的速度大小为10m/s,求他到达C点前、后的瞬时加速度(不计各种阻力).
在长0.2m的细绳的一端系一小球,绳的另一端固定在水平桌面上,使小球以大小为0.6m/s的线速度在桌面上做匀速圆周运动,则小球运动的角速度和向心加速度分别多大?
走时准确的时钟(指针看作匀速圆周运动),分针与时针长度之比是1.2:1.
(1)分针与时针角速度之比路多少?
(2)分针与时针转速之比是多少?
(3)分针针尖与时针针尖的线速度之比是多少?
(4)分针和时针转动的向心加速度之比是多少?
答案和解析
1.【答案】A
【解答】
A.时间相同,路程之比即线速度大小之比,故A项正确;
B.运动方向改变的角度之比即对应扫过的圆心角之比,由于时间相同,角速度大小之比也为3∶2,B项错误;
C.路程比除以角度比得半径比为8∶9,C项错误;
D.由向心加速度a=v2r知线速度平方比除以半径比即向心加速度大小之比为2∶1,D项错误。
故选A.
2.【答案】D
【解答】
A.做匀速圆周运动的物体要受到指向圆心的向心力的作用,向心力大小不变,方向时刻变化,所以向心加速度的方向始终指向圆心,在不同的时刻方向是不同的,而大小不变,故A错误;
B.只有做匀速圆周运动的物体,加速度一定指向圆心,故B错误;
C.向心加速度是描述速度的方向变化快慢的物理量,向心加速度越大,物体速度方向变化越快,故C错误;
D.匀速圆周运动速度的方向不断变化,不属于匀速运动,故D正确
故选D。
3.【答案】B
【解析】解:根据公式a=ω2r和ω=2πT,有:a=4π2rT2
甲、乙两个物体都做匀速圆周运动,转动半径之比为9:4,转动的周期之比为3:4,故它们的向心加速度之比为:
a甲a乙=r甲r乙?(T乙T甲)2=94×(43)2=4:1
4.【答案】D
【解答】
①轮A、轮B靠摩擦传动,边缘点线速度相等,故:
va:vb=1:1
根据公式v=rω,有:
ωa:ωb=3:2
根据ω=2πn,有:
na:nb=3:2
根据a=vω,有:
aa:ab=3:2
②轮B、轮C是共轴传动,角速度相等,故:
ωb:ωc=1:1
根据公式v=rω,有:
vb:vc=3:2
根据ω=2πn,有:
nb:nc=1:1
根据a=vω,有:
ab:ac=3:2
综合得到:
va:vb:vc=3:3:2
ωa:ωb:ωc=3:2:2
na:nb:nc=3:2:2
aa:ab:ac=9:6:4
故选D。
5.【答案】A
【解析】解:小球沿圆环运动,其运动轨迹就是圆环所在的圆,轨迹的圆心就是圆环的圆心,运动轨迹的半径就是圆环的半径,小球运动到环的最低点时,其向心加速度的大小为ν2R,加速度方向竖直向上,故A正确,B、C、D错误.
6.【答案】B
【解答】
根据题意有两轮边缘上的线速度大小相等,即有vA=vB
A.根据角速度ω和线速度v的关系v=rω得角速度与半径成反比:即ωAωB=RBRA=12,故A错误;
B.根据向心加速度a与线速度v的关系a=v2R得,因为vA=vB所以:aAaB=RBRA=12,故B正确;
C.根据同期T和线速度v的关系T=2πRv得,因为vA=vB所以:TATB=RARB=21,故C错误。
D.根据转速n和线速度v的关系v=2πnR得:因为vA=vB所以:nAnB=RBRA=12,故D错误。
故选B。
7.【答案】B
【解析】解:A.P、Q两点是传送带传动的两轮子边缘上两点,则vP=vQ,而rP>rQ,v=rω,所以P、Q两点角速度大小不相等,故A错误;
B、P、Q是传送带两轮子边缘上的两点,故其线速度大小相等,所以B正确;
CD、因为vP=vQ,而rP>rQ,向心加速度a=v2r知,Q点向心加速度大于P向心加速度,故CD均错误。
8.【答案】D
【解答】
A.根据万有引力提供向心力得出:GMmr2=m4π2rT2得:M=4π2r3GT2,根据图象可知,A的r3T2比B的大,所以行星A的质量大于行星B的质量,故A错误;
B.根据图象可知,在两颗行星表面做匀速圆周运动的周期相同,密度ρ=MV=3πGT02,所以行星A的密度等于行星B的密度,故B错误;
C.第一宇宙速度v=2πRT0,A的半径大于B的半径,卫星环绕行星表面运行的周期相同,则A的第一宇宙速度大于行星B的第一宇宙速度,故C错误;
D.根据GMmr2=ma得:a=GMr2,当两行星的卫星轨道半径相同时,A的质量大于B的质量,则行星A的卫星向心加速度大于行星B的卫星向心加速,故D正确。
故选D。
9.【答案】C
【解析】解:A、小孩相对圆盘静止,一起和圆盘做圆周运动,由静摩擦力提供向心力,故A错误;
B、设P点到圆心的距离为r,圆盘的转速为n,则角速度为ω=2πn,小孩随圆盘一起做圆周运动,由静摩擦力提供向心力,根据牛顿第二定律可得小孩所受静摩擦力的大小为f=mrω2=4mrπ2n2,故B错误;
C、若小孩随圆盘一起做变速圆周运动,小孩所受重力和支持力是一对平衡力,其中摩擦力沿半径方向的分力提供向心加速度使小孩做圆周运动,沿切线方向的分力提供切向加速度使小孩的速度大小变化,所以摩擦力的方向不指向圆心,故C正确;
D、若小孩在距离圆心更近的另一点相对圆盘静止,则小孩做圆周运动的半径减小,根据f=mrω2可知,小孩受到的摩擦力减小,故D错误。
10.【答案】D
【解答】
A.对其中一个小球受力分析,如图所示,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;将重力与拉力合成,合力指向圆心,由几何关系得合力:F=mgtan?θ,①? ? θ不同,则F大小不同,故A错误;
D.由向心力公式得:F=mω2r,②? ?设绳子与悬挂点间的高度差为h,由几何关系,得:r=?tan?θ,③? ? 由①②③得,ω=g?,可知角速度与绳子的长度和转动半径无关,两球角速度相同,故D正确;
B.又由T=2πω可知两球运动周期相同,故B错误;
C.由v=ωr可知,两球转动半径不等,线速度大小不同,故C错误。
故选D。
11.【答案】B
【解答】
B、依据a=ω2R,物块运动的角速度:ω=aR=2rad/s,故B正确;
A、周期T=2πω=πs,故A错误;
C、根据v=ωr,知v=2m/s,小球在πs内通过的路程为l=vt=2πm,故C错误;
D、质点运动的周期为πs,即在π4s内物块转过14圆,通过的位移大小为:x=2R=2m,故D错误。
故选B。
12.【答案】C
【解析】解:摩擦轮A和C通过中介轮B进行传动,三个轮子边缘上的点线速度大小相等。根据ω=vr,A、C两轮边缘上的点半径之比为2:1,则角速度之比为1:2.根据a=v2r知,A、C两轮半径之比为2:1,则向心加速度之比为1:2,根据ω=2πT知,A、C两轮角速度之比为1:2,则周期之比为2:1,故C正确,ABD错误。
故选:C。
摩擦轮A和C通过中介轮B进行传动,抓住线速度大小相等,根据ω=vr,a=v2r、ω=2πT求出角速度、向心加速度和周期之比。
解决本题的关键抓住线速度大小相等,根据线速度与角速度、向心加速度的关系进行分析。
13.【答案】CD
【解析】
【分析】
解决本题的关键知道线速度、角速度、向心加速度与半径的关系,知道大齿轮和小齿轮的线速度大小相等,难度适中。
大齿轮和小齿轮的线速度大小相等,小齿轮的运动方向和大齿轮的运动方向相同,根据v=ωr判断角速度的关系,根据a=v2r判断向心加速度的关系。
【解答】
A.小齿轮的运动方向和大齿轮的运动方向相同,所以小齿轮是顺时针匀速转动,故A错误;
B.大齿轮和小齿轮的线速度大小相等,小齿轮的每个齿的线速度方向不同,故B错误;
C.根据v=ωr可知,线速度相等,大齿轮半径(内径)是小齿轮半径的3倍时,小齿轮的角速度是大齿轮角速度的3倍,故C正确;
D.根据a=v2r,大齿轮半径(内径)是小齿轮半径的3倍.可知小齿轮每个齿的向心加速度是大齿轮每个齿的向心加速度的3倍,故D正确。
故选CD。
14.【答案】BC
【解析】解:AB、因为A、B离轴距离均为R,C距离轴为2R,A、B、C三个物体的角速度相等,根据公式a=ω2R知aA=aBCD、因为A、B、C三个物体的角速度相等根据摩擦力提供向心力,对A:fA=3mω2R,对B:fB=mω2R,对C:fC=mω2?2R,可得:fA>fC>fB,故C正确,D错误。
故选:BC。
物体做圆周运动靠静摩擦力提供向心力,三个物体和圆盘一起做圆周运动,角速度相等,根据a=ω2R比较向心加速度的大小,根据牛顿第二定律比较摩擦力的大小。
本题可从三个物体中选择任意一个物体,建立物理模型后分析比较,而不需要对三个物体分别分析,难度适中,注意本题由于是静摩擦,故不能用μFN求解摩擦力。
15.【答案】AC
【解析】解:A、球在竖直平面内做圆周运动,根据ω=vr,碰到钉子的瞬间线速度v不变,半径变小,故角速度ω变大,故A正确;
B、细绳碰到钉子,半径减半,圆周运动的圆心变为P点,由于只是细绳碰到钉子,小球并未受到水平力作用可改变速度大小,即小球的线速度大小不变,故B错误;
CD、根据a=v2r,线速度v不变,半径变小,故向心加速度a增大,故C正确,D错误;
16.【答案】ABD
【解答】
A.两把手的加速度方向相同的时刻有两个,a转到1位置与b转到5位置和α转到3位置与b转到7位置,故A正确;
B.两把手的角速度方向相同的时刻有两个,a转到2位置与b转到6位置和a转到4位置与b转到8位置,故B正确;
C.题中两把手均做匀速圆周运动,线速度沿切线方向,有方向相同的时刻,故C错误;
D.两个把手做匀速圆周运动,所受合力提供向心力,线速度转动半径和质量都相等,根据公式Fn=mν2r知向心力大小相等,故D正确.
17.【答案】BCD
【解答】
A.做匀速圆周运动的物体的加速度大小不变,方向不断变化,选项A错误;
B.匀速圆周运动的速度方向不断变化,是变速运动,选项B正确;
C.向心加速度方向一定指向圆心,选项C正确;
D.根据ν=ωr可知,物体做半径一定的匀速圆周运动时,其线速度大小与角速度成正比,选项D正确。
18.【答案】解:已知频闪仪的闪光频率为30Hz,
由题意可知,转动周期T=6×130s=0.2s
周期T=2πω
解得:ω=2πT=10πrad/s;
向心加速度为:
19.【答案】解:运动员经圆弧轨道滑到C点前做圆周运动.因为不计各种阻力,故经过C点之前的瞬间运动员所受合力方向竖直向上,由an=ν2r得运动员到达C点前的瞬时加速度a1=1022?m/s?2=50m/s,方向竖直向上.运动员滑过C点后,进入水平轨道做匀速直线运动,故加速度a2=0.
答案:50m/s2,方向竖直向上? 0
20.【答案】解:小球做匀速圆周运动
根据v=ωr
得ω=vr=0.60.2=3rad/s
向心加速度公式a=ω2r=1.8m/s2
21.【答案】解:(1)在一个小时的时间内,分针每转过的角度为360度,而时针转过的角度为30度,
所以角速度之比为:ω1:ω2=360:30=12:1;
(2)根据ω=2πn可知,n=ω2π,故n1:n2=12:1;
(3)由v=rω可得,线速度之比为v1:v2=1.2×12:1×1=14.4:1;
(4)根据a=vω知,向心加速度之比为a1:a2=172.8:1。
答:(1)分针与时针的角速度之比是12:1;
(2)分针与时针转速之比是12:1
(3)分针针尖与时针针尖的线速度之比是14.4:1;
(4)分针和时针转动的向心加速度之比是172.8:1.
一、单选题
A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4:3,运动方向改变的角度之比是3:2,则它们的(????)
A. 线速度大小之比为4:3 B. 角速度之比为3:4
C. 圆周运动半径之比为2:1 D. 向心加速度大小之比为1:2
关于向心加速度,下列说法正确的是(????)
A. 由an=ν2r知,匀速圆周运动的向心加速度恒定
B. 做圆周运动的物体,加速度时刻指向圆心
C. 向心加速度越大,物体速率变化越快
D. 匀速圆周运动不属于匀速运动
甲、乙两个物体都做匀速圆周运动,转动半径之比为9:4,转动的周期之比为3:4,则它们所受的向心加速度之比为(????)
A. 1:4 B. 4:1 C. 4:9 D. 9:4
如下图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB∶RC=3∶2.A轮的半径与C轮相同,它与B轮紧靠在一起.当A轮绕其中心的竖直轴转动时,由于摩擦作用,B轮也会随之无滑动地转动.a、b、c分别为三个转轮A、B、C边缘上的三个点,在运动过程中,a、b、c三点的(??? )
A. 线速度大小之比为3∶2∶2 B. 角速度大小之比为3∶3∶2
C. 转速之比为2∶3∶2 D. 向心加速度大小之比为9∶6∶4
如下图所示,半径为R的圆环竖直放置,一轻弹簧一端固定在环的最高点A,另一端系一带有小孔穿在环上的小球,弹簧原长为23R将小球从静止开始释放,释放时弹簧恰无形变,小球运动到环的最低点时速率为ν,这时小球向心加速度的大小为(??? )
A. ν2R
B. ν22R
C. 3ν22R
D. 3ν24R
如图所示,A、B为啮合传动的两齿轮,RA=2RB,则A、B两轮边缘上两点的(????)
A. 角速度之比为2∶1 B. 向心加速度之比为1∶2
C. 周期之比为1∶2 D. 转速之比为2∶1
如图所示是自行车的轮盘与车轴上的飞轮之间的链条传动装置.P是轮盘的一个齿,Q是飞轮上的一个齿.下列说法中正确的是(????)
A. P、Q两点角速度大小相等
B. P、Q两点线速度大小相等
C. P、Q两点向心加速度大小相等
D. P点向心加速度大于Q点向心加速度
假设宇宙中有两颗相距无限远的行星A和B,半径分别为RA和RB两颗行星周围卫星的轨道半径的三次方(r3)与运行周期的平方(T2)的关系如图所示,T0为卫星环绕行星表面运行的周期。则(??? )
A. 行星A的质量小于行星B的质量
B. 行星A的密度小于行星B的密度
C. 行星A的第一宇宙速度等于行星B的第一宇宙速度
D. 当两行星的卫星轨道半径相同时,行星A的卫星向心加速度大于行星B的卫星向心加速度
如下图所示,公园的“魔法旋转圆盘”绕过圆心的竖直轴在水平面内匀速转动,一小孩站在圆盘上某处的P点(非圆心)相对圆盘静止.下列说法正确的是(????)
A. 小孩在P点相对圆盘静止,因此他不受摩擦力作用
B. 若使圆盘以较小的转速(不为零)转动,则小孩在P点受到的摩擦力为零
C. 若小孩随圆盘一起做变速圆周运动,则其所受摩擦力方向不指向圆心
D. 若小孩在距离圆心更近的另一点相对圆盘静止且圆盘转速不变,则小孩受到的摩擦力增大
如图所示,两个质量相同的小球用长度不等的不可伸长的细线拴在同一点,并在同一水平面内做同方向的匀速圆周运动,则它们的(????)
A. 向心力大小相同
B. 运动周期不同
C. 运动线速度大小相同
D. 运动角速度相同
如图所示,一小物块以大小为4?m/s2的向心加速度做匀速圆周运动,半径R=1?m,则下列说法正确的是(??? )
A. 小物块做圆周运动的周期为1?s
B. 小物块运动的角速度为2?rad/s
C. 小物块在π?s内通过的路程为零
D. 小物块在t=π4s内通过的位移大小为π20m
如图所示,一个传动装置中有三个紧挨着的摩擦轮A、B和C,B为主动轮,A和C均为从动轮,它们的半径分别为:rA=8cm,rB=6cm,rC=4cm,则两个从动轮在主动轮的带动下不打滑转动时,A、C两个从动轮边缘上的质点(????)
A. 线速度之比vA:vC=2:1
B. 角速度之比为ωA:ωC=2:1
C. 周期之比为TA:TC=2:1
D. 向心加速度之比为aA:aC=2:1
二、多选题
(多选)某实验楼大厅里科普器材中有如下图所示的传动装置:在大齿轮盘内嵌有三个等大的小齿轮.若齿轮的齿很小,大齿轮半径(内径)是小齿轮半径的3倍,则当大齿轮顺时针匀速转动时,下列说法正确的是(????)
A. 小齿轮逆时针匀速转动
B. 小齿轮的每个齿的线速度均相同
C. 小齿轮的角速度是大齿轮角速度的3倍
D. 小齿轮每个齿的向心加速度是大齿轮每个齿的向心加速度的3倍
如图所示,A、B、C三个物体放在旋转平台上随平台一起做匀速圆周运动,动摩擦因数均为μ,已知A的质量为3m,B、C的质量均为m,A、B离轴距离均为R,C距离轴为2R,则以下说法正确的是(????)
A. aA=aC>aB B. aA=aB
如图所示,长为L的细绳一端固定在O点,另一端拴住一个小球,在O点的正下方与O点相距L2的地方有一枚与竖直平面垂直的钉子,把球拉起使细绳在水平方向伸直,由静止开始释放,当细绳碰到钉子的瞬间,下列说法正确的是(????)
A. 小球的角速度突然增大 B. 小球的线速度突然增大
C. 小球的向心加速度突然增大 D. 小球的向心加速度不变
(多选)如下图所示是健身活动器械“太极推揉器”上的两个圆环,两圆环在同一个平面内,能绕各自的轴O1、O2转动.健身的人手握环边缘上的把手a、b转动圆环,达到活动手臂关节的目的.今活动者手握把手,按图中标出的转动方向和角速度匀速转动圆环,在从图示位置开始的一周的转动过程中,关于两把手(质量相同,两圆环和把手关于cd对称)的有关情况,下列说法正确的是(??? )
A. 两把手的加速度方向相同的时刻有两个
B. 两把手的角速度方向相同的时刻有两个
C. 两把手的线速度方向总是相反的
D. 两把手所受合力大小相等
(多选)关于做匀速圆周运动的物体,下列说法正确的是(????)
A. 角速度、周期、转速、加速度均恒定不变
B. 匀速圆周运动是变速运动
C. 向心加速度方向一定指向圆心
D. 物体做半径一定的匀速圆周运动时,其线速度大小与角速度成正比
三、计算题
一圆柱形小物块放在水平转盘上,并随着转盘一起绕O点匀速转动.通过频闪照相技术对其进行研究,从转盘的正上方拍照,得到转盘转动一周的频闪照片如下图所示,已知频闪仪的闪光频率为30Hz,转动半径为2m,则该转盘转动的角速度和物块的向心加速度是多少?
如下图所示,某滑板运动员恰好从B点进入半径为2m的14圆弧轨道,该圆弧轨道在C点与水平轨道相接,运动员滑到C点时的速度大小为10m/s,求他到达C点前、后的瞬时加速度(不计各种阻力).
在长0.2m的细绳的一端系一小球,绳的另一端固定在水平桌面上,使小球以大小为0.6m/s的线速度在桌面上做匀速圆周运动,则小球运动的角速度和向心加速度分别多大?
走时准确的时钟(指针看作匀速圆周运动),分针与时针长度之比是1.2:1.
(1)分针与时针角速度之比路多少?
(2)分针与时针转速之比是多少?
(3)分针针尖与时针针尖的线速度之比是多少?
(4)分针和时针转动的向心加速度之比是多少?
答案和解析
1.【答案】A
【解答】
A.时间相同,路程之比即线速度大小之比,故A项正确;
B.运动方向改变的角度之比即对应扫过的圆心角之比,由于时间相同,角速度大小之比也为3∶2,B项错误;
C.路程比除以角度比得半径比为8∶9,C项错误;
D.由向心加速度a=v2r知线速度平方比除以半径比即向心加速度大小之比为2∶1,D项错误。
故选A.
2.【答案】D
【解答】
A.做匀速圆周运动的物体要受到指向圆心的向心力的作用,向心力大小不变,方向时刻变化,所以向心加速度的方向始终指向圆心,在不同的时刻方向是不同的,而大小不变,故A错误;
B.只有做匀速圆周运动的物体,加速度一定指向圆心,故B错误;
C.向心加速度是描述速度的方向变化快慢的物理量,向心加速度越大,物体速度方向变化越快,故C错误;
D.匀速圆周运动速度的方向不断变化,不属于匀速运动,故D正确
故选D。
3.【答案】B
【解析】解:根据公式a=ω2r和ω=2πT,有:a=4π2rT2
甲、乙两个物体都做匀速圆周运动,转动半径之比为9:4,转动的周期之比为3:4,故它们的向心加速度之比为:
a甲a乙=r甲r乙?(T乙T甲)2=94×(43)2=4:1
4.【答案】D
【解答】
①轮A、轮B靠摩擦传动,边缘点线速度相等,故:
va:vb=1:1
根据公式v=rω,有:
ωa:ωb=3:2
根据ω=2πn,有:
na:nb=3:2
根据a=vω,有:
aa:ab=3:2
②轮B、轮C是共轴传动,角速度相等,故:
ωb:ωc=1:1
根据公式v=rω,有:
vb:vc=3:2
根据ω=2πn,有:
nb:nc=1:1
根据a=vω,有:
ab:ac=3:2
综合得到:
va:vb:vc=3:3:2
ωa:ωb:ωc=3:2:2
na:nb:nc=3:2:2
aa:ab:ac=9:6:4
故选D。
5.【答案】A
【解析】解:小球沿圆环运动,其运动轨迹就是圆环所在的圆,轨迹的圆心就是圆环的圆心,运动轨迹的半径就是圆环的半径,小球运动到环的最低点时,其向心加速度的大小为ν2R,加速度方向竖直向上,故A正确,B、C、D错误.
6.【答案】B
【解答】
根据题意有两轮边缘上的线速度大小相等,即有vA=vB
A.根据角速度ω和线速度v的关系v=rω得角速度与半径成反比:即ωAωB=RBRA=12,故A错误;
B.根据向心加速度a与线速度v的关系a=v2R得,因为vA=vB所以:aAaB=RBRA=12,故B正确;
C.根据同期T和线速度v的关系T=2πRv得,因为vA=vB所以:TATB=RARB=21,故C错误。
D.根据转速n和线速度v的关系v=2πnR得:因为vA=vB所以:nAnB=RBRA=12,故D错误。
故选B。
7.【答案】B
【解析】解:A.P、Q两点是传送带传动的两轮子边缘上两点,则vP=vQ,而rP>rQ,v=rω,所以P、Q两点角速度大小不相等,故A错误;
B、P、Q是传送带两轮子边缘上的两点,故其线速度大小相等,所以B正确;
CD、因为vP=vQ,而rP>rQ,向心加速度a=v2r知,Q点向心加速度大于P向心加速度,故CD均错误。
8.【答案】D
【解答】
A.根据万有引力提供向心力得出:GMmr2=m4π2rT2得:M=4π2r3GT2,根据图象可知,A的r3T2比B的大,所以行星A的质量大于行星B的质量,故A错误;
B.根据图象可知,在两颗行星表面做匀速圆周运动的周期相同,密度ρ=MV=3πGT02,所以行星A的密度等于行星B的密度,故B错误;
C.第一宇宙速度v=2πRT0,A的半径大于B的半径,卫星环绕行星表面运行的周期相同,则A的第一宇宙速度大于行星B的第一宇宙速度,故C错误;
D.根据GMmr2=ma得:a=GMr2,当两行星的卫星轨道半径相同时,A的质量大于B的质量,则行星A的卫星向心加速度大于行星B的卫星向心加速,故D正确。
故选D。
9.【答案】C
【解析】解:A、小孩相对圆盘静止,一起和圆盘做圆周运动,由静摩擦力提供向心力,故A错误;
B、设P点到圆心的距离为r,圆盘的转速为n,则角速度为ω=2πn,小孩随圆盘一起做圆周运动,由静摩擦力提供向心力,根据牛顿第二定律可得小孩所受静摩擦力的大小为f=mrω2=4mrπ2n2,故B错误;
C、若小孩随圆盘一起做变速圆周运动,小孩所受重力和支持力是一对平衡力,其中摩擦力沿半径方向的分力提供向心加速度使小孩做圆周运动,沿切线方向的分力提供切向加速度使小孩的速度大小变化,所以摩擦力的方向不指向圆心,故C正确;
D、若小孩在距离圆心更近的另一点相对圆盘静止,则小孩做圆周运动的半径减小,根据f=mrω2可知,小孩受到的摩擦力减小,故D错误。
10.【答案】D
【解答】
A.对其中一个小球受力分析,如图所示,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;将重力与拉力合成,合力指向圆心,由几何关系得合力:F=mgtan?θ,①? ? θ不同,则F大小不同,故A错误;
D.由向心力公式得:F=mω2r,②? ?设绳子与悬挂点间的高度差为h,由几何关系,得:r=?tan?θ,③? ? 由①②③得,ω=g?,可知角速度与绳子的长度和转动半径无关,两球角速度相同,故D正确;
B.又由T=2πω可知两球运动周期相同,故B错误;
C.由v=ωr可知,两球转动半径不等,线速度大小不同,故C错误。
故选D。
11.【答案】B
【解答】
B、依据a=ω2R,物块运动的角速度:ω=aR=2rad/s,故B正确;
A、周期T=2πω=πs,故A错误;
C、根据v=ωr,知v=2m/s,小球在πs内通过的路程为l=vt=2πm,故C错误;
D、质点运动的周期为πs,即在π4s内物块转过14圆,通过的位移大小为:x=2R=2m,故D错误。
故选B。
12.【答案】C
【解析】解:摩擦轮A和C通过中介轮B进行传动,三个轮子边缘上的点线速度大小相等。根据ω=vr,A、C两轮边缘上的点半径之比为2:1,则角速度之比为1:2.根据a=v2r知,A、C两轮半径之比为2:1,则向心加速度之比为1:2,根据ω=2πT知,A、C两轮角速度之比为1:2,则周期之比为2:1,故C正确,ABD错误。
故选:C。
摩擦轮A和C通过中介轮B进行传动,抓住线速度大小相等,根据ω=vr,a=v2r、ω=2πT求出角速度、向心加速度和周期之比。
解决本题的关键抓住线速度大小相等,根据线速度与角速度、向心加速度的关系进行分析。
13.【答案】CD
【解析】
【分析】
解决本题的关键知道线速度、角速度、向心加速度与半径的关系,知道大齿轮和小齿轮的线速度大小相等,难度适中。
大齿轮和小齿轮的线速度大小相等,小齿轮的运动方向和大齿轮的运动方向相同,根据v=ωr判断角速度的关系,根据a=v2r判断向心加速度的关系。
【解答】
A.小齿轮的运动方向和大齿轮的运动方向相同,所以小齿轮是顺时针匀速转动,故A错误;
B.大齿轮和小齿轮的线速度大小相等,小齿轮的每个齿的线速度方向不同,故B错误;
C.根据v=ωr可知,线速度相等,大齿轮半径(内径)是小齿轮半径的3倍时,小齿轮的角速度是大齿轮角速度的3倍,故C正确;
D.根据a=v2r,大齿轮半径(内径)是小齿轮半径的3倍.可知小齿轮每个齿的向心加速度是大齿轮每个齿的向心加速度的3倍,故D正确。
故选CD。
14.【答案】BC
【解析】解:AB、因为A、B离轴距离均为R,C距离轴为2R,A、B、C三个物体的角速度相等,根据公式a=ω2R知aA=aB
故选:BC。
物体做圆周运动靠静摩擦力提供向心力,三个物体和圆盘一起做圆周运动,角速度相等,根据a=ω2R比较向心加速度的大小,根据牛顿第二定律比较摩擦力的大小。
本题可从三个物体中选择任意一个物体,建立物理模型后分析比较,而不需要对三个物体分别分析,难度适中,注意本题由于是静摩擦,故不能用μFN求解摩擦力。
15.【答案】AC
【解析】解:A、球在竖直平面内做圆周运动,根据ω=vr,碰到钉子的瞬间线速度v不变,半径变小,故角速度ω变大,故A正确;
B、细绳碰到钉子,半径减半,圆周运动的圆心变为P点,由于只是细绳碰到钉子,小球并未受到水平力作用可改变速度大小,即小球的线速度大小不变,故B错误;
CD、根据a=v2r,线速度v不变,半径变小,故向心加速度a增大,故C正确,D错误;
16.【答案】ABD
【解答】
A.两把手的加速度方向相同的时刻有两个,a转到1位置与b转到5位置和α转到3位置与b转到7位置,故A正确;
B.两把手的角速度方向相同的时刻有两个,a转到2位置与b转到6位置和a转到4位置与b转到8位置,故B正确;
C.题中两把手均做匀速圆周运动,线速度沿切线方向,有方向相同的时刻,故C错误;
D.两个把手做匀速圆周运动,所受合力提供向心力,线速度转动半径和质量都相等,根据公式Fn=mν2r知向心力大小相等,故D正确.
17.【答案】BCD
【解答】
A.做匀速圆周运动的物体的加速度大小不变,方向不断变化,选项A错误;
B.匀速圆周运动的速度方向不断变化,是变速运动,选项B正确;
C.向心加速度方向一定指向圆心,选项C正确;
D.根据ν=ωr可知,物体做半径一定的匀速圆周运动时,其线速度大小与角速度成正比,选项D正确。
18.【答案】解:已知频闪仪的闪光频率为30Hz,
由题意可知,转动周期T=6×130s=0.2s
周期T=2πω
解得:ω=2πT=10πrad/s;
向心加速度为:
19.【答案】解:运动员经圆弧轨道滑到C点前做圆周运动.因为不计各种阻力,故经过C点之前的瞬间运动员所受合力方向竖直向上,由an=ν2r得运动员到达C点前的瞬时加速度a1=1022?m/s?2=50m/s,方向竖直向上.运动员滑过C点后,进入水平轨道做匀速直线运动,故加速度a2=0.
答案:50m/s2,方向竖直向上? 0
20.【答案】解:小球做匀速圆周运动
根据v=ωr
得ω=vr=0.60.2=3rad/s
向心加速度公式a=ω2r=1.8m/s2
21.【答案】解:(1)在一个小时的时间内,分针每转过的角度为360度,而时针转过的角度为30度,
所以角速度之比为:ω1:ω2=360:30=12:1;
(2)根据ω=2πn可知,n=ω2π,故n1:n2=12:1;
(3)由v=rω可得,线速度之比为v1:v2=1.2×12:1×1=14.4:1;
(4)根据a=vω知,向心加速度之比为a1:a2=172.8:1。
答:(1)分针与时针的角速度之比是12:1;
(2)分针与时针转速之比是12:1
(3)分针针尖与时针针尖的线速度之比是14.4:1;
(4)分针和时针转动的向心加速度之比是172.8:1.
