5.3平行线的判定及性质-2020-2021学年人教版七年级数学下册专题复习提升训练(含答案)
文档属性
| 名称 | 5.3平行线的判定及性质-2020-2021学年人教版七年级数学下册专题复习提升训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 609.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 10:52:58 | ||
图片预览




文档简介
专题复习提升训练卷5.3平行线的判定及性质-20-21人教版七年级数学下册
一、选择题
1、如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
(2) (3) (4)
2、如图,∠1=120°,要使a∥b,则∠2的大小是 ( )
A.60° B.80° C.100° D.120°
3、如图,在下列给出的条件中,不能判定AB∥CD的是 ( )
A.∠BAD+∠ADC=180° B.∠ABD=∠BDC C.∠ADB=∠DBC D.∠ABE=∠DCE
4、如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
5、如图,下列条件中,不能判定直线a∥b的是 ( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠2=∠3
(6) (7) (8)
6、如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为 ( )
A.135° B.90° C.60° D.45°
7、如图,,则下列结论错误的是( )
A. B. C. D.
8、小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
9、如图,在下列给出的条件中,能判定的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
(10) (11)
10、如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
11、如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有 .
12、如图,下列条件:中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
13、如图,如果∠BAC=∠ ,那么根据 ,?可得AB∥CD;
如果∠BAD+∠ =180°或∠D+∠ =180°,那么根据 ,可得AD∥BC.?
(14) (15)
14、如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4= .
15、如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转________度.
16、如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD= °.
(17) (18)
17、如图?b,M、N分别在、上,为两平行线间一点,那么
A.180 B.270 C.360 D.540
18、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有 .(只填序号)
19、如图,,于点,若,则的度数是______.
(19) (20)
20、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
三、解答题
21、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22、如图,∠1=60°,∠2=60°,∠3=120°.试说明:(1)DE∥BC;(2)DF∥AB.
23、填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(________________)
即=∠______________
∵∠3=∠4,(已知)
∴∠3=∠______(_______________)
∴∠3=∠______
∴(____________________)
24、在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.
求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ),
∵DE∥BC(已证),
∴ ,( )
又∵∠1=∠2(已知),
∴ ,( )
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
25、如图,已知∠1+∠2=180°,∠A=∠C,证明:AF∥CE.
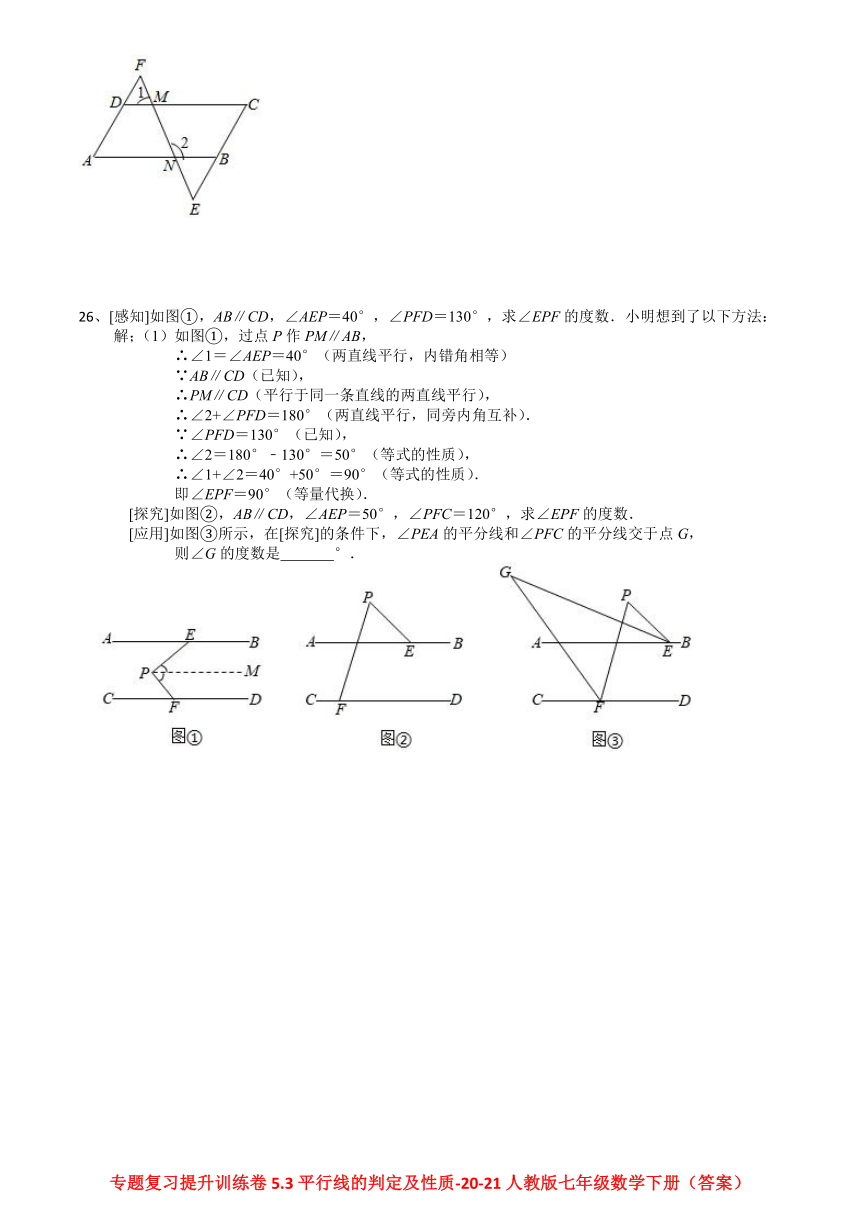
26、[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,
则∠G的度数是 °.
专题复习提升训练卷5.3平行线的判定及性质-20-21人教版七年级数学下册(答案)
一、选择题
1、如图,下列推理错误的是( D )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
2、如图,∠1=120°,要使a∥b,则∠2的大小是 ( D )
A.60° B.80° C.100° D.120°
3、如图,在下列给出的条件中,不能判定AB∥CD的是 ( C )
A.∠BAD+∠ADC=180° B.∠ABD=∠BDC C.∠ADB=∠DBC D.∠ABE=∠DCE
4、如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( C )
A.80° B.90° C.100° D.110°
5、如图,下列条件中,不能判定直线a∥b的是 ( D )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠2=∠3
6、如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为 ( D )
A.135° B.90° C.60° D.45°
7、如图,,则下列结论错误的是( )
A. B. C. D.
【答案】由∠1=∠2=65°,可得内错角相等,两直线平行,故A选项正确,
∠3和∠BFE互为对顶角,∴∠BFE=35°,∠1为△BEF的外角,
∴∠1=∠BFE+∠B,可得∠B=30°,故B选项正确.
∠EFC为△CFG的外角,∴∠EFC=∠C+∠CGF,故C选项错误.
因为在△CGF中,∠CFG>∠C,∴CG>FG,故D选项正确,
所以本题答案为C
8、小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( A. )
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
9、如图,在下列给出的条件中,能判定的是( C )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
10、如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,其中正确的有( D )
A.1个 B.2个 C.3个 D.4个
11、如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有 ②③④ .
12、如图,下列条件:中能判断直线的有( B)
A.5个 B.4个 C.3个 D.2个
二、填空题
13、如图,如果∠BAC=∠ ,那么根据 ,?可得AB∥CD;
如果∠BAD+∠ =180°或∠D+∠ =180°,那么根据 ,可得AD∥BC.?
【答案】ACD 内错角相等,两直线平行
B DCB 同旁内角互补,两直线平行
14、如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4= 70° .
15、如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转___15 ______度.
16、如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD= 65 °.
17、如图?b,、分别在、上,为两平行线间一点,那么 C
A.180 B.270 C.360 D.540
18、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有 ①②④ .(只填序号)
19、如图,,于点,若,则的度数是__130______.
20、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
解:∵AB∥CD,∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,∴∠1+∠3=45°,
∵∠5=∠2+∠3,∴∠5=∠1+∠3=45°,即∠BFD=45°,
故答案为:45°.
三、解答题
21、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
解:∵EF∥AD,AD∥BC,∴EF∥BC,∴∠ACB+∠DAC=180°,
∵∠DAC=120°,∴∠ACB=60°,
又∵∠ACF=20°,∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,∴∠BCE=20°,
∵EF∥BC,∴∠FEC=∠ECB,∴∠FEC=20°.
22、如图,∠1=60°,∠2=60°,∠3=120°.试说明:(1)DE∥BC;(2)DF∥AB.
解:(1)∵∠1=60°,∠2=60°,∴∠1=∠2,
∴DE∥BC(同位角相等,两直线平行).
(2)如图,∵∠1=60°,∴∠4=∠1=60°.
∵∠3=120°,∴∠3+∠4=180°,
∴DF∥AB(同旁内角互补,两直线平行).
23、填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(________________)
即=∠______________
∵∠3=∠4,(已知)
∴∠3=∠______(_______________)
∴∠3=∠______
∴(____________________)
解:∵∠1=∠2(已知)
∴(__等式的性质______________)
即=∠___CAD___________
∵∠3=∠4,(已知)
∴∠3=∠__BAE____(___等量代换____________)
∴∠3=∠__CAD____
∴(_____内错角相等,两直线平行_______________)
24、在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.
求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ),
∵DE∥BC(已证),
∴ ,( )
又∵∠1=∠2(已知),
∴ ,( )
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
【解析】证明:∵∠ADE=∠B(已知),
∴DE∥BC(同位角相等,两直线平行),
∵DE∥BC(已证),
∴∠1=∠DCB,(两直线平行,内错角相等)
又∵∠1=∠2(已知),
∴∠DCB=∠2,(等量代换)
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;∠1=∠DCB;两直线平行,内错角相等;
∠DCB=∠2;等量代换.
25、如图,已知∠1+∠2=180°,∠A=∠C,证明:AF∥CE.
解:∵∠1=∠CMN(对顶角相等),
又∵∠1+∠2=180°(已知),
∴∠2+∠CMN=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠A=∠FDC(两直线平行,同位角相等),
∵∠A=∠C(已知),
∴∠FDC=∠C(等量代换),
∴AF∥CE(内错角相等,两直线平行).
26、[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,
则∠G的度数是 °.
【解答】[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知), ∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣MPE=120°50°=70°(等式的性质).
答:∠EPF的度数为70°;
[应用]如图③所示,∵EG是∠PEA的平分线,PG是∠PFC的平分线,
∴∠AEGAEP=25°,∠GCFPFC=60°,
过点G作GM∥AB,∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣MGE=60°﹣25°=35°.
答:∠G的度数是35°. 故答案为:35.
一、选择题
1、如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
(2) (3) (4)
2、如图,∠1=120°,要使a∥b,则∠2的大小是 ( )
A.60° B.80° C.100° D.120°
3、如图,在下列给出的条件中,不能判定AB∥CD的是 ( )
A.∠BAD+∠ADC=180° B.∠ABD=∠BDC C.∠ADB=∠DBC D.∠ABE=∠DCE
4、如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
5、如图,下列条件中,不能判定直线a∥b的是 ( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠2=∠3
(6) (7) (8)
6、如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为 ( )
A.135° B.90° C.60° D.45°
7、如图,,则下列结论错误的是( )
A. B. C. D.
8、小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
9、如图,在下列给出的条件中,能判定的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
(10) (11)
10、如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
11、如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有 .
12、如图,下列条件:中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
13、如图,如果∠BAC=∠ ,那么根据 ,?可得AB∥CD;
如果∠BAD+∠ =180°或∠D+∠ =180°,那么根据 ,可得AD∥BC.?
(14) (15)
14、如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4= .
15、如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转________度.
16、如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD= °.
(17) (18)
17、如图?b,M、N分别在、上,为两平行线间一点,那么
A.180 B.270 C.360 D.540
18、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有 .(只填序号)
19、如图,,于点,若,则的度数是______.
(19) (20)
20、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
三、解答题
21、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22、如图,∠1=60°,∠2=60°,∠3=120°.试说明:(1)DE∥BC;(2)DF∥AB.
23、填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(________________)
即=∠______________
∵∠3=∠4,(已知)
∴∠3=∠______(_______________)
∴∠3=∠______
∴(____________________)
24、在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.
求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ),
∵DE∥BC(已证),
∴ ,( )
又∵∠1=∠2(已知),
∴ ,( )
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
25、如图,已知∠1+∠2=180°,∠A=∠C,证明:AF∥CE.
26、[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,
则∠G的度数是 °.
专题复习提升训练卷5.3平行线的判定及性质-20-21人教版七年级数学下册(答案)
一、选择题
1、如图,下列推理错误的是( D )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
2、如图,∠1=120°,要使a∥b,则∠2的大小是 ( D )
A.60° B.80° C.100° D.120°
3、如图,在下列给出的条件中,不能判定AB∥CD的是 ( C )
A.∠BAD+∠ADC=180° B.∠ABD=∠BDC C.∠ADB=∠DBC D.∠ABE=∠DCE
4、如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( C )
A.80° B.90° C.100° D.110°
5、如图,下列条件中,不能判定直线a∥b的是 ( D )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠2=∠3
6、如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为 ( D )
A.135° B.90° C.60° D.45°
7、如图,,则下列结论错误的是( )
A. B. C. D.
【答案】由∠1=∠2=65°,可得内错角相等,两直线平行,故A选项正确,
∠3和∠BFE互为对顶角,∴∠BFE=35°,∠1为△BEF的外角,
∴∠1=∠BFE+∠B,可得∠B=30°,故B选项正确.
∠EFC为△CFG的外角,∴∠EFC=∠C+∠CGF,故C选项错误.
因为在△CGF中,∠CFG>∠C,∴CG>FG,故D选项正确,
所以本题答案为C
8、小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( A. )
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
9、如图,在下列给出的条件中,能判定的是( C )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
10、如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,其中正确的有( D )
A.1个 B.2个 C.3个 D.4个
11、如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有 ②③④ .
12、如图,下列条件:中能判断直线的有( B)
A.5个 B.4个 C.3个 D.2个
二、填空题
13、如图,如果∠BAC=∠ ,那么根据 ,?可得AB∥CD;
如果∠BAD+∠ =180°或∠D+∠ =180°,那么根据 ,可得AD∥BC.?
【答案】ACD 内错角相等,两直线平行
B DCB 同旁内角互补,两直线平行
14、如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4= 70° .
15、如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转___15 ______度.
16、如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD= 65 °.
17、如图?b,、分别在、上,为两平行线间一点,那么 C
A.180 B.270 C.360 D.540
18、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有 ①②④ .(只填序号)
19、如图,,于点,若,则的度数是__130______.
20、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
解:∵AB∥CD,∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,∴∠1+∠3=45°,
∵∠5=∠2+∠3,∴∠5=∠1+∠3=45°,即∠BFD=45°,
故答案为:45°.
三、解答题
21、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
解:∵EF∥AD,AD∥BC,∴EF∥BC,∴∠ACB+∠DAC=180°,
∵∠DAC=120°,∴∠ACB=60°,
又∵∠ACF=20°,∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,∴∠BCE=20°,
∵EF∥BC,∴∠FEC=∠ECB,∴∠FEC=20°.
22、如图,∠1=60°,∠2=60°,∠3=120°.试说明:(1)DE∥BC;(2)DF∥AB.
解:(1)∵∠1=60°,∠2=60°,∴∠1=∠2,
∴DE∥BC(同位角相等,两直线平行).
(2)如图,∵∠1=60°,∴∠4=∠1=60°.
∵∠3=120°,∴∠3+∠4=180°,
∴DF∥AB(同旁内角互补,两直线平行).
23、填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(________________)
即=∠______________
∵∠3=∠4,(已知)
∴∠3=∠______(_______________)
∴∠3=∠______
∴(____________________)
解:∵∠1=∠2(已知)
∴(__等式的性质______________)
即=∠___CAD___________
∵∠3=∠4,(已知)
∴∠3=∠__BAE____(___等量代换____________)
∴∠3=∠__CAD____
∴(_____内错角相等,两直线平行_______________)
24、在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.
求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ),
∵DE∥BC(已证),
∴ ,( )
又∵∠1=∠2(已知),
∴ ,( )
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
【解析】证明:∵∠ADE=∠B(已知),
∴DE∥BC(同位角相等,两直线平行),
∵DE∥BC(已证),
∴∠1=∠DCB,(两直线平行,内错角相等)
又∵∠1=∠2(已知),
∴∠DCB=∠2,(等量代换)
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;∠1=∠DCB;两直线平行,内错角相等;
∠DCB=∠2;等量代换.
25、如图,已知∠1+∠2=180°,∠A=∠C,证明:AF∥CE.
解:∵∠1=∠CMN(对顶角相等),
又∵∠1+∠2=180°(已知),
∴∠2+∠CMN=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠A=∠FDC(两直线平行,同位角相等),
∵∠A=∠C(已知),
∴∠FDC=∠C(等量代换),
∴AF∥CE(内错角相等,两直线平行).
26、[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,
则∠G的度数是 °.
【解答】[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知), ∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣MPE=120°50°=70°(等式的性质).
答:∠EPF的度数为70°;
[应用]如图③所示,∵EG是∠PEA的平分线,PG是∠PFC的平分线,
∴∠AEGAEP=25°,∠GCFPFC=60°,
过点G作GM∥AB,∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣MGE=60°﹣25°=35°.
答:∠G的度数是35°. 故答案为:35.
