高中数学——定积分的概念常考试题解析讲解

(共17张PPT)
高中数学—定积分的概念
1.5.1　曲边梯形的面积常考试题解析
1.5.2　汽车行驶的路程常考试题解析
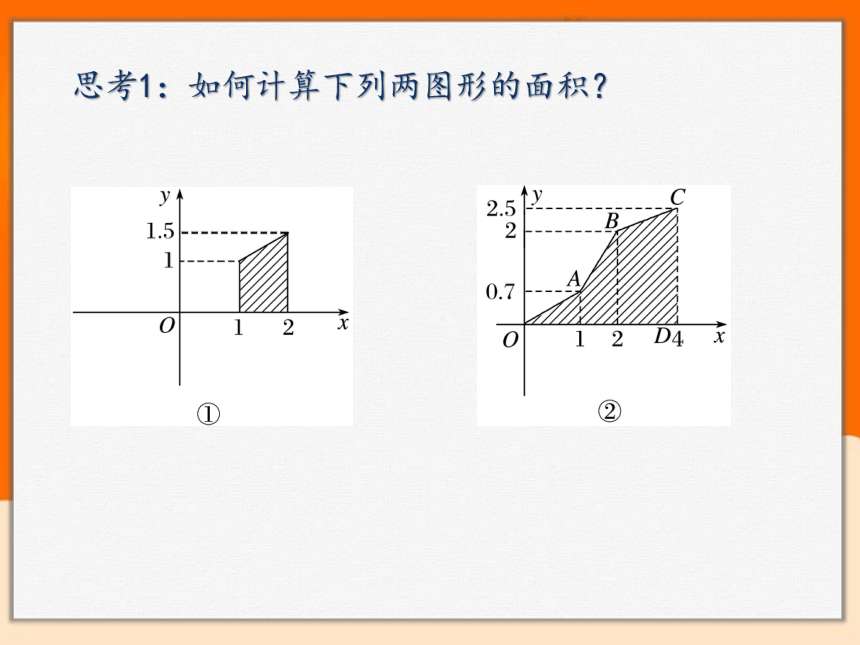
思考1：如何计算下列两图形的面积？
思考2：如图，为求由抛物线与直线，所围成的平面图形的面积，图形与我们熟悉的“直边图形”有什么区别？
曲边梯形，曲边梯形的一条边为曲线段，而“直边图形”的所有边都是直线段.
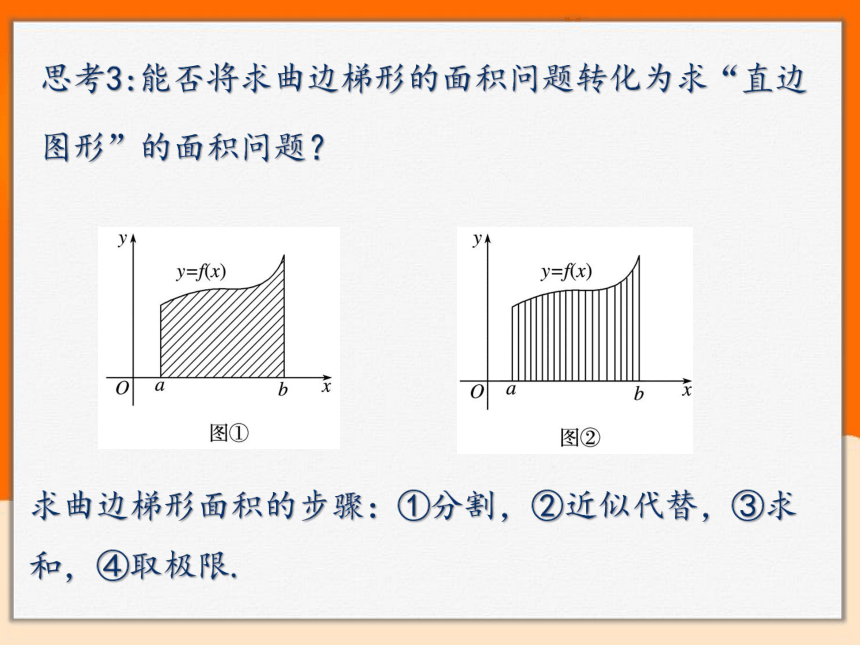
思考3:能否将求曲边梯形的面积问题转化为求“直边图形”的面积问题？
求曲边梯形面积的步骤：①分割，②近似代替，③求和，④取极限.
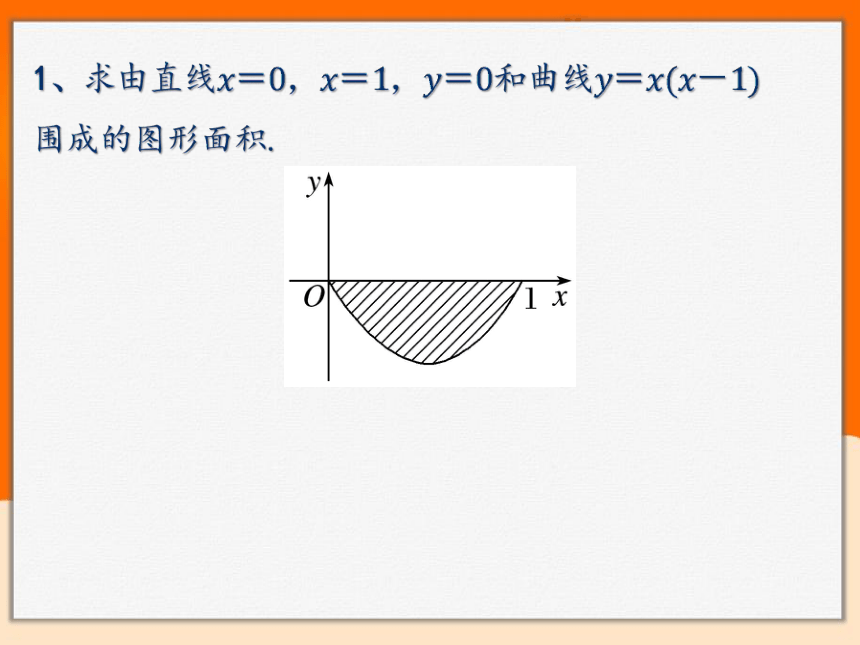
1、求由直线，，和曲线围成的图形面积.
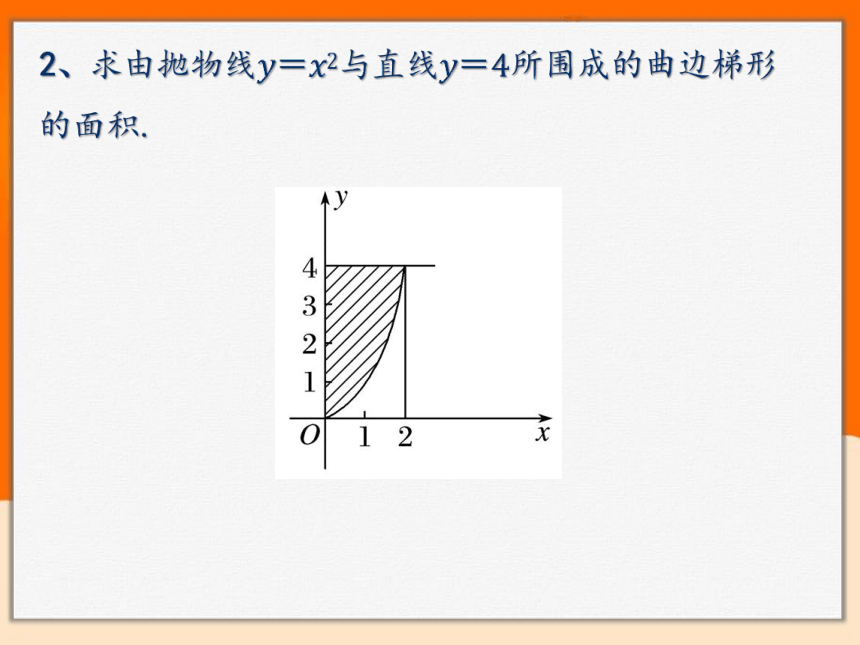
2、求由抛物线与直线所围成的曲边梯形的面积.
求变速直线运动的(位移)路程
如果物体做变速直线运动，速度函数为，那么也可以采用分割、近似代替、求和、取极限的方法，求出它在内所作的位移.
1.有一辆汽车在笔直的公路上变速行驶，在时刻t的速度为(单位：)，那么该汽车在(单位：)这段时间内行驶的路程(单位：)是多少？
2.一辆汽车在笔直的公路上变速行驶，设汽车在时刻的速度为(的单位：，的单位：)，试计算这辆汽车在这段时间内汽车行驶的路程(单位：).
求曲边梯形面积和汽车行驶的路程的步骤：
(1)分割：n等分区间[a，b]；
(2)近似代替：取点ξi∈[xi－1，xi]；
(4)取极限：
“近似代替”也可以用较大的矩形来代替曲边梯形，为了计算方便，可以取区间上的一些特殊点，如区间的端点(或中点).
一般地，设函数在区间上连续，用分点将区间等分成个小区间，在每个小区间上任取一点，作和式,，当时，上述和式无限接近某个常数，这个常数叫做函数在区间上的定积分，记作，即，这里，与分别叫做积分下限与积分上限，区间叫做积分区间，函数叫做被积函数，叫做积分变量，叫做被积式.
(1)当函数时，定积分表示由直线，，及曲线所围成的曲边梯形的面积.
(2)当函数时,曲边梯形位于轴的下方,此时等于曲边梯形面积的相反数,即.
(3)当在区间上有正有负时，定积分表示介于轴、函数的图象及直线，之间各部分面积的代数和(在轴上方的取正，在轴下方的取负).
从几何上看，如果在区间上函数连续且恒有，那么定积分表示由直线，，和曲线所围成的曲边梯形的面积.这就是定积分的几何意义.
直线把一个大的曲边梯形分成了两个小曲边梯形，因此大曲边梯形的面积是两个小曲边梯形的面积，之和，即.
(1)(为常数)
(2)
(3)
1.定积分的大小(　　)
A.与和积分区间有关，与的取法无关
B.与有关，与区间及的取法无关
C.与及的取法有关，与区间无关
D.与、积分区间和的取法都有关
2.用定积分的定义计算.
3.用定义计算.
4.如图所示，在区间上，则阴影部分的面积为(　　)
A.
B.
C.
D.
5.利用定积分的几何意义计算
6.计算的值.
7.已知，，，求：
(1)；(2)
(3)