3.4 高中物理受力分析-力的合成与分解 29张PPT
文档属性
| 名称 | 3.4 高中物理受力分析-力的合成与分解 29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 774.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-16 08:05:24 | ||
图片预览








文档简介
(共29张PPT)
受力分析
力的合成与分解
一、受力分析
概念:把研究对象在指定的物理环境中受到的所有力都分析出来,并画出物体所受的力的
,这个过程就是受力分析。
受力分析的重要依据:
1、寻找对它的施力物体;
2、寻找产生的原因;
3、寻找是否改变物体的运动状态(即是否产生加速度)或改变物体的形状
示意图
受力分析的一般顺序:
一般先分析场力(重力、电场力、磁场力);
然后分析弹力,环绕物体一周,找出跟研究对象接触的物体,并逐个分析这些物体对研究对象是否有弹力作用;
最后分析摩擦力,对凡有弹力作用的地方逐一进行分析。
二、力的合成
1.合力与分力
(1)、定义:当一个物体受到几个力的共同作用时,
我们常常可以求出这样一个力,这个力产生的效
果跟原来几个力的共同效果相同,这个力就叫做
那几个力的
,原来的几个力叫做
.
(2)、逻辑关系:合力和分力是一种
关系.
2、共点力:作用在物体的
,或作用线的
交于一点的力.
3、力的合成:求几个力的
的过程.
合力
分力
等效替代
同一点
延长
线
合力
4.力的运算法则:
(1)平行四边形定则:求两个互成角度的
的合力,可以用表示这两个力的线段为邻边作
,这两个邻边之间的对角线就表示合
力的
和
.
(2)三角形定则:把两个矢量
从而求出
合矢量的方法(如图1所示).
共点力
平
行四边形
方向
首尾相接
大小
图1
1、合力不一定大于分力
2、合力与它的分力是力的效果上的一种等效替代
关系
三、力的分解
1、概念:求一个力的
的过程.
2、遵循原则:
定则或
定则.
3、分解的方法:
(1)按力产生的
进行分解.
(2)
分解.
分力
平等四边形
三角形
正交
效果
受力分析常用的方法及步骤
1、整体法与隔离法
整体法
隔离法
概念
将加速度相同的几个
物体作为一个整体来
分析的方法
将研究对象与周
围物体分隔开分
析的方法
选用
原则
研究系统外的物体对
系统整体的作用力或
系统整体的加速度
研究系统内物体
之间的相互作用
力
注意
问题
受力分析时不要再考
虑系统内物体间的相
互作用力
一般隔离受力较
少的物体
2、假设法:
在受力分析时,若不能确定某力是否存在,可先对其作出存在或不存在的情况假设,然后再就该力存在与否对物体运动状态影响的不同来判断该力是否存在。
整体法、隔离法在受力分析时要灵活选用:
1、当所涉及的物理问题是整体与外界作用时,应用整体分析法,可使问题简单明了,而不必考虑内力的作用。
2、当涉及的物理问题是物体间的作用时,要应用隔离分析法,这时系统中物体间相互作用的内力就会变为各个独立物体的外力。
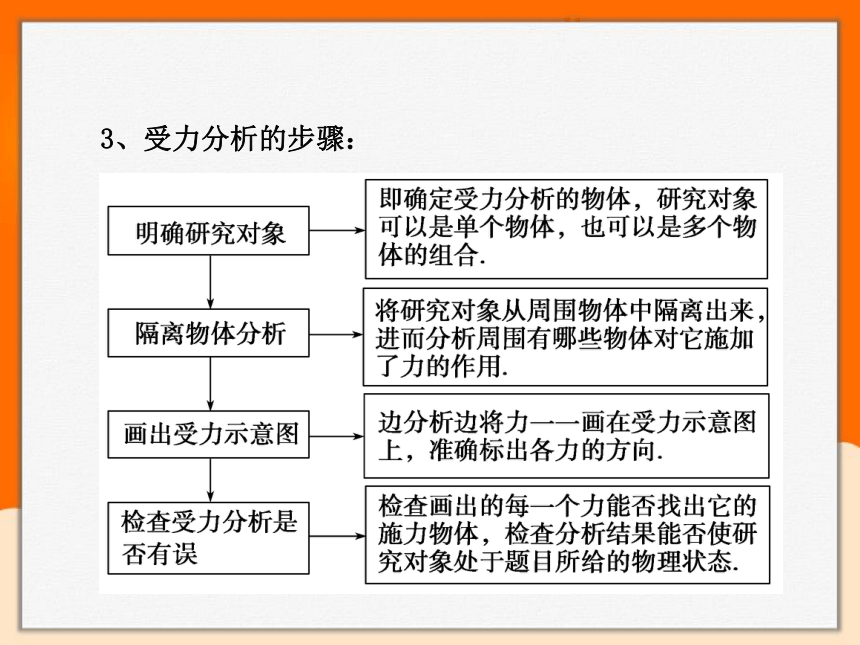
3、受力分析的步骤:
共点力合成的方法及合力范围的确定
1、共点力合成的常用方法
(1)作图法:
从力的作用点沿两个分力的作用方向按同一标度作出两个分力F1、F2,以这两个力为邻边作一个平行四边形,这两个力所夹对角线表示这两个力的合力.通常可分别用刻度尺和量角器直接量出合力的大小和方向。
(2)解析法
根据力的平行四边形定则作出力的合成的图示,
如图所示:
它与F2的夹角为θ.
以下是合力计算的几种特殊情况:
1、相互垂直的两个力的合成,如图所示.
由几何知识可知合力大小为
方向
2、夹角为θ的大小相同的两个力的合成,如图所示:
由几何知识,作出的平行四边形为菱形,其对角线相互垂直且平分,则合力大小
方向与
F1夹角为
3、夹角为120°的两等大的力的合成,如图所示:
由几何知识得出对角线将画出的平行四边形分为两个等边三角形,故合力的大小与分力相等。
2、合力范围的确定
(1)两个共点力的合成:
|F1-F2|≤F合≤F1+F2
即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小,为|F1-F2|,当两力同向时,合力最大,为F1+F2
(2)三个共点力的合成:
①三个力共线且同向时,其合力最大,为F1+F2+F3
②任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力的最小值为零,如果第三个力不在这个范围内,则合力的最小值为最大的一个力减去另外两个较小的力的和的绝对值。
1、合成力时,要注意正确理解合力与分力的关系:
(1)效果关系:合力的作用效果与各分力共同的作
用效果相同,它们具有等效替代性。
(2)大小关系:合力与分力谁大要视情况而定,不能
形成合力总大于分力的定势思维。
2、三个共点力合成时,其合力的最小值不一定等于
两个较小力的和减去第三个较大的力。
力的分解的两种方法
1、按力的效果分解:
(1)根据力的实际作用效果确定两个实际分力的方向;
(2)再根据两个实际分力方向画出平行四边形;
(3)最后由平行四边形知识求出两分力的大小,如图所示,物体的重力G按产生的效果分解为两个分力,F1使物体下滑,F2使物体压向斜面。
2、正交分解法:
(1)定义:把一个力分解为相互垂直的分力的方法。
(2)优点:把物体所受的不同方向的各个力都分解到相互垂直的两个方向上去,然后再求每个方向上的分力的代数和,这样就把复杂的矢量运算转化成了简单的代数运算,最后再求两个互成90°角的力的合力就简便多了。
(3)运用正交分解法解题的步骤:
①正确选择直角坐标系,通常选择共点力的作用点为坐标原点,直角坐标x、y的选择可按下列原则去确定:
(a)尽可能使更多的力落在坐标轴上.
(b)沿物体运动方向或加速度方向设置一个坐标轴。
(c)若各种设置效果一样,则沿水平方向、竖直方向
设置两坐标轴。
②正交分解各力,即分别将各力投影到坐标轴上,
分别求x轴和y轴上各力投影的合力Fx和Fy,其中
Fx=F1x+F2x+F3x+…;Fy=F1y+F2y+F3y+…
③求Fx与Fy的合力即为共点力的合力(如图所示)
合力大小:
合力的方向与x轴夹角:θ=arctan
受力分析的基本思路
如图所示,物体A靠在倾斜的墙面上,在与墙面和B垂直的力F作用下,A、B保持静止,试分析A、B两物
体受力的个数。
解析:先取B为研究对象,把A看作墙的一部分,受
力如下图所示:
若只受GB和F,B物体不能静止,因此A对B有沿接触面向上的静摩擦力f1,受f1则一定有A对B的弹力N,B受4个力作用。
取AB整体为研究对象,同理可得墙对A有沿墙面向上的静摩擦力f2和墙的弹力NA
由牛顿第三定律知A还受B的斜向下的静摩擦力f1′和垂直接触面向上的弹力N′,还有自身的重力GA,共5个力。
答案:A受5个力,B受4个力
按力的作用效果分解
如图10所示,α=30°,装置的重力和摩擦力均不计,若用F=100
N的水平推力使滑块B保持静止,则工件上受到的向上的弹力多大?
根据力的实际效果分解力的思维路线:
解析:对B受力分析如图甲得:F2sin
α=F
又F2与F2′为作用力与反作用力,故F2′=F2可得:
由牛顿第三定律得:
工件受到的向上的弹力为100
N.
对装置上部分受力分析如图乙,其中N为工件对
装置的压力.得:N=F2′cos
α
力的合成法在平衡问题中的应用
如图12所示是骨折病人的牵引装置示意图,绳的一端固定,
绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内。
为了使脚所受的拉力增大,可采取的方法是
(
)
A、只增加绳的长度
B、只增加重物的质量
C、只将病人的脚向右移动
D、只将两定滑轮的间距增大
解析:取动滑轮为研究对象,受力分
析如右图所示,F1、F2为绳子的拉力,
F为帆布带的拉力.动滑轮静止时,所
受合外力为零,即F1与F2合力与F等大反向。
只要F1、F2的合力增大,F就增大。当绳的长度增加时,绳的拉力及绳间的夹角不变,合力不变,A错;
当增加重物质量时,绳拉力增大,夹角不变,合力增大,B对;
病人的脚右移时,绳间的夹角增大,合力减小,C错;
定滑轮间距增大时,夹角增大,合力减小,D错。
答案:B
如图所示,
在轻质细线的下端悬挂一个质量为m的物体,若用力F拉物体,使细线偏离竖直方向的夹角为α,且始终保持α角不变,求拉力F的最小值?
当F垂直于力T时,F有最小值,Fmin=F′sinα,因
F′=mg,故Fmin=mgsin
α.
答案:mgsin
α
解析:以物体为研究对象,始终保持α角不变,说明:
处于静止状态.物体受到的细线的张力T与拉力F的合力F′与物体的重力等大反向。
由于细线的张力T和合力F′的方向均不变,
根据各力的特点可组成矢量三角形如右图
所示,由图解可以看出:
总结
受力分析
力的合成与分解
一、受力分析
概念:把研究对象在指定的物理环境中受到的所有力都分析出来,并画出物体所受的力的
,这个过程就是受力分析。
受力分析的重要依据:
1、寻找对它的施力物体;
2、寻找产生的原因;
3、寻找是否改变物体的运动状态(即是否产生加速度)或改变物体的形状
示意图
受力分析的一般顺序:
一般先分析场力(重力、电场力、磁场力);
然后分析弹力,环绕物体一周,找出跟研究对象接触的物体,并逐个分析这些物体对研究对象是否有弹力作用;
最后分析摩擦力,对凡有弹力作用的地方逐一进行分析。
二、力的合成
1.合力与分力
(1)、定义:当一个物体受到几个力的共同作用时,
我们常常可以求出这样一个力,这个力产生的效
果跟原来几个力的共同效果相同,这个力就叫做
那几个力的
,原来的几个力叫做
.
(2)、逻辑关系:合力和分力是一种
关系.
2、共点力:作用在物体的
,或作用线的
交于一点的力.
3、力的合成:求几个力的
的过程.
合力
分力
等效替代
同一点
延长
线
合力
4.力的运算法则:
(1)平行四边形定则:求两个互成角度的
的合力,可以用表示这两个力的线段为邻边作
,这两个邻边之间的对角线就表示合
力的
和
.
(2)三角形定则:把两个矢量
从而求出
合矢量的方法(如图1所示).
共点力
平
行四边形
方向
首尾相接
大小
图1
1、合力不一定大于分力
2、合力与它的分力是力的效果上的一种等效替代
关系
三、力的分解
1、概念:求一个力的
的过程.
2、遵循原则:
定则或
定则.
3、分解的方法:
(1)按力产生的
进行分解.
(2)
分解.
分力
平等四边形
三角形
正交
效果
受力分析常用的方法及步骤
1、整体法与隔离法
整体法
隔离法
概念
将加速度相同的几个
物体作为一个整体来
分析的方法
将研究对象与周
围物体分隔开分
析的方法
选用
原则
研究系统外的物体对
系统整体的作用力或
系统整体的加速度
研究系统内物体
之间的相互作用
力
注意
问题
受力分析时不要再考
虑系统内物体间的相
互作用力
一般隔离受力较
少的物体
2、假设法:
在受力分析时,若不能确定某力是否存在,可先对其作出存在或不存在的情况假设,然后再就该力存在与否对物体运动状态影响的不同来判断该力是否存在。
整体法、隔离法在受力分析时要灵活选用:
1、当所涉及的物理问题是整体与外界作用时,应用整体分析法,可使问题简单明了,而不必考虑内力的作用。
2、当涉及的物理问题是物体间的作用时,要应用隔离分析法,这时系统中物体间相互作用的内力就会变为各个独立物体的外力。
3、受力分析的步骤:
共点力合成的方法及合力范围的确定
1、共点力合成的常用方法
(1)作图法:
从力的作用点沿两个分力的作用方向按同一标度作出两个分力F1、F2,以这两个力为邻边作一个平行四边形,这两个力所夹对角线表示这两个力的合力.通常可分别用刻度尺和量角器直接量出合力的大小和方向。
(2)解析法
根据力的平行四边形定则作出力的合成的图示,
如图所示:
它与F2的夹角为θ.
以下是合力计算的几种特殊情况:
1、相互垂直的两个力的合成,如图所示.
由几何知识可知合力大小为
方向
2、夹角为θ的大小相同的两个力的合成,如图所示:
由几何知识,作出的平行四边形为菱形,其对角线相互垂直且平分,则合力大小
方向与
F1夹角为
3、夹角为120°的两等大的力的合成,如图所示:
由几何知识得出对角线将画出的平行四边形分为两个等边三角形,故合力的大小与分力相等。
2、合力范围的确定
(1)两个共点力的合成:
|F1-F2|≤F合≤F1+F2
即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小,为|F1-F2|,当两力同向时,合力最大,为F1+F2
(2)三个共点力的合成:
①三个力共线且同向时,其合力最大,为F1+F2+F3
②任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力的最小值为零,如果第三个力不在这个范围内,则合力的最小值为最大的一个力减去另外两个较小的力的和的绝对值。
1、合成力时,要注意正确理解合力与分力的关系:
(1)效果关系:合力的作用效果与各分力共同的作
用效果相同,它们具有等效替代性。
(2)大小关系:合力与分力谁大要视情况而定,不能
形成合力总大于分力的定势思维。
2、三个共点力合成时,其合力的最小值不一定等于
两个较小力的和减去第三个较大的力。
力的分解的两种方法
1、按力的效果分解:
(1)根据力的实际作用效果确定两个实际分力的方向;
(2)再根据两个实际分力方向画出平行四边形;
(3)最后由平行四边形知识求出两分力的大小,如图所示,物体的重力G按产生的效果分解为两个分力,F1使物体下滑,F2使物体压向斜面。
2、正交分解法:
(1)定义:把一个力分解为相互垂直的分力的方法。
(2)优点:把物体所受的不同方向的各个力都分解到相互垂直的两个方向上去,然后再求每个方向上的分力的代数和,这样就把复杂的矢量运算转化成了简单的代数运算,最后再求两个互成90°角的力的合力就简便多了。
(3)运用正交分解法解题的步骤:
①正确选择直角坐标系,通常选择共点力的作用点为坐标原点,直角坐标x、y的选择可按下列原则去确定:
(a)尽可能使更多的力落在坐标轴上.
(b)沿物体运动方向或加速度方向设置一个坐标轴。
(c)若各种设置效果一样,则沿水平方向、竖直方向
设置两坐标轴。
②正交分解各力,即分别将各力投影到坐标轴上,
分别求x轴和y轴上各力投影的合力Fx和Fy,其中
Fx=F1x+F2x+F3x+…;Fy=F1y+F2y+F3y+…
③求Fx与Fy的合力即为共点力的合力(如图所示)
合力大小:
合力的方向与x轴夹角:θ=arctan
受力分析的基本思路
如图所示,物体A靠在倾斜的墙面上,在与墙面和B垂直的力F作用下,A、B保持静止,试分析A、B两物
体受力的个数。
解析:先取B为研究对象,把A看作墙的一部分,受
力如下图所示:
若只受GB和F,B物体不能静止,因此A对B有沿接触面向上的静摩擦力f1,受f1则一定有A对B的弹力N,B受4个力作用。
取AB整体为研究对象,同理可得墙对A有沿墙面向上的静摩擦力f2和墙的弹力NA
由牛顿第三定律知A还受B的斜向下的静摩擦力f1′和垂直接触面向上的弹力N′,还有自身的重力GA,共5个力。
答案:A受5个力,B受4个力
按力的作用效果分解
如图10所示,α=30°,装置的重力和摩擦力均不计,若用F=100
N的水平推力使滑块B保持静止,则工件上受到的向上的弹力多大?
根据力的实际效果分解力的思维路线:
解析:对B受力分析如图甲得:F2sin
α=F
又F2与F2′为作用力与反作用力,故F2′=F2可得:
由牛顿第三定律得:
工件受到的向上的弹力为100
N.
对装置上部分受力分析如图乙,其中N为工件对
装置的压力.得:N=F2′cos
α
力的合成法在平衡问题中的应用
如图12所示是骨折病人的牵引装置示意图,绳的一端固定,
绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内。
为了使脚所受的拉力增大,可采取的方法是
(
)
A、只增加绳的长度
B、只增加重物的质量
C、只将病人的脚向右移动
D、只将两定滑轮的间距增大
解析:取动滑轮为研究对象,受力分
析如右图所示,F1、F2为绳子的拉力,
F为帆布带的拉力.动滑轮静止时,所
受合外力为零,即F1与F2合力与F等大反向。
只要F1、F2的合力增大,F就增大。当绳的长度增加时,绳的拉力及绳间的夹角不变,合力不变,A错;
当增加重物质量时,绳拉力增大,夹角不变,合力增大,B对;
病人的脚右移时,绳间的夹角增大,合力减小,C错;
定滑轮间距增大时,夹角增大,合力减小,D错。
答案:B
如图所示,
在轻质细线的下端悬挂一个质量为m的物体,若用力F拉物体,使细线偏离竖直方向的夹角为α,且始终保持α角不变,求拉力F的最小值?
当F垂直于力T时,F有最小值,Fmin=F′sinα,因
F′=mg,故Fmin=mgsin
α.
答案:mgsin
α
解析:以物体为研究对象,始终保持α角不变,说明:
处于静止状态.物体受到的细线的张力T与拉力F的合力F′与物体的重力等大反向。
由于细线的张力T和合力F′的方向均不变,
根据各力的特点可组成矢量三角形如右图
所示,由图解可以看出:
总结
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
