2020-2021学年高二下学期数学人教A版选择性必修第三册8.1.2样本相关系数课件(共21张PPT)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版选择性必修第三册8.1.2样本相关系数课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览







文档简介
8.1.2 样本相关系数
复习回顾
在散点图中,点散布在从左下角到右上角的区域,我们将它称为正相关.
点散布在从左上角到右下角的区域,我们将它称为负相关.
1、两个变量相关关系与散点图中的点散布区域的关系
2.线性相关
3.非线性相关
一般地, 如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关。
两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关。
一般情形下, 表明成对样本数据正相关;
表明成对样本数据负相关.
复习回顾
复习回顾
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
重点:通过样本相关系数判断或比较成对数据的相关性强弱
难点:做出成对数据的散点图,求样本相关系数,理解样本相关系数的统计含义
学习目标
思考:当|r|=1时,成对样本数据之间具有怎样的关系呢?
思考:当|r|=1时,成对样本数据之间具有怎样的关系呢?
当|r|越接近1时,成对样本数据的相关程度越强;
当|r|越接近0时,成对样本数据的相关程度越弱.
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
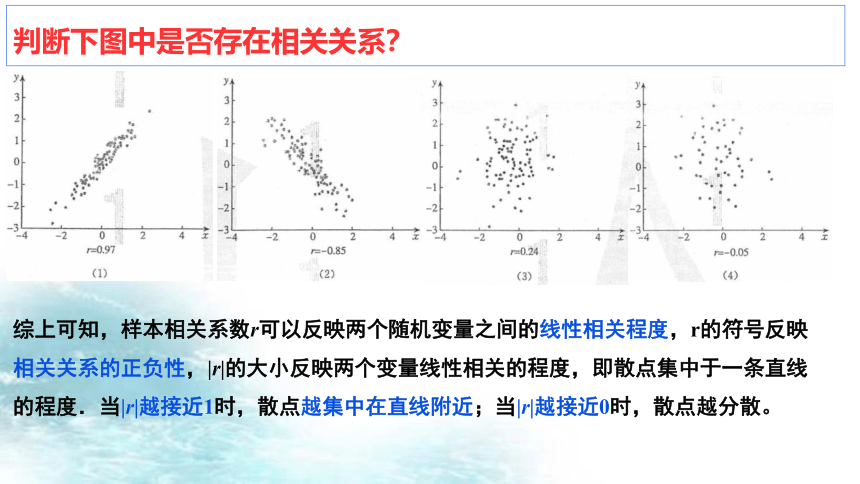
判断下图中是否存在相关关系?
综上可知,样本相关系数r可以反映两个随机变量之间的线性相关程度,r的符号反映相关关系的正负性,|r|的大小反映两个变量线性相关的程度,即散点集中于一条直线的程度.当|r|越接近1时,散点越集中在直线附近;当|r|越接近0时,散点越分散。
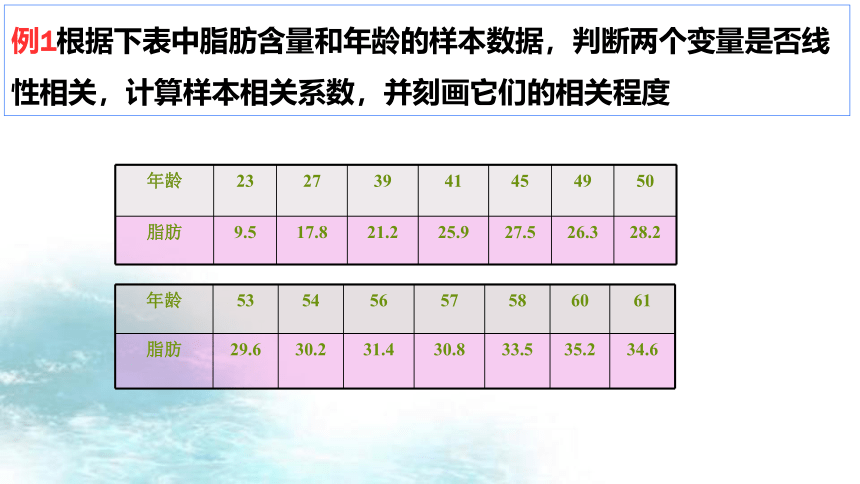
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
解:先画出散点图,如下图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}第n年
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系。
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
利用计算工具可得:
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
利用计算工具可得:
由样本数据计算得样本相关系数 ,由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强。
【例】对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )
A.r2 C.r4A
习题应用
习题应用
计算下面问题的样本相关系数:
课堂小结
样本相关系数性质:
r的符号反映相关关系的正负性,
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
课堂小结
样本相关系数性质:
当|r|=1时,两个变量之间满足一种线性关系.
当|r|越接近1时,成对样本数据的相关程度越强,散点越集中在一条直线附近;
当|r|越接近0时,成对样本数据的相关程度越弱.散点越杂乱无章,越分散。
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
课下作业
1、学案卷(样本相关系数应用)
2、课本103页练习T2、T3、T4
复习回顾
在散点图中,点散布在从左下角到右上角的区域,我们将它称为正相关.
点散布在从左上角到右下角的区域,我们将它称为负相关.
1、两个变量相关关系与散点图中的点散布区域的关系
2.线性相关
3.非线性相关
一般地, 如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关。
两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关。
一般情形下, 表明成对样本数据正相关;
表明成对样本数据负相关.
复习回顾
复习回顾
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
重点:通过样本相关系数判断或比较成对数据的相关性强弱
难点:做出成对数据的散点图,求样本相关系数,理解样本相关系数的统计含义
学习目标
思考:当|r|=1时,成对样本数据之间具有怎样的关系呢?
思考:当|r|=1时,成对样本数据之间具有怎样的关系呢?
当|r|越接近1时,成对样本数据的相关程度越强;
当|r|越接近0时,成对样本数据的相关程度越弱.
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
判断下图中是否存在相关关系?
综上可知,样本相关系数r可以反映两个随机变量之间的线性相关程度,r的符号反映相关关系的正负性,|r|的大小反映两个变量线性相关的程度,即散点集中于一条直线的程度.当|r|越接近1时,散点越集中在直线附近;当|r|越接近0时,散点越分散。
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
解:先画出散点图,如下图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
例1根据下表中脂肪含量和年龄的样本数据,判断两个变量是否线性相关,计算样本相关系数,并刻画它们的相关程度
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}第n年
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系。
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
利用计算工具可得:
例2有人收集了某城市居民年收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示
利用计算工具可得:
由样本数据计算得样本相关系数 ,由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强。
【例】对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是( )
A.r2
习题应用
习题应用
计算下面问题的样本相关系数:
课堂小结
样本相关系数性质:
r的符号反映相关关系的正负性,
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
课堂小结
样本相关系数性质:
当|r|=1时,两个变量之间满足一种线性关系.
当|r|越接近1时,成对样本数据的相关程度越强,散点越集中在一条直线附近;
当|r|越接近0时,成对样本数据的相关程度越弱.散点越杂乱无章,越分散。
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
课下作业
1、学案卷(样本相关系数应用)
2、课本103页练习T2、T3、T4
