1.3线段的垂直平分线-2020-2021学年北师大版八年级数学下册同步提升训练(Word版含解析)
文档属性
| 名称 | 1.3线段的垂直平分线-2020-2021学年北师大版八年级数学下册同步提升训练(Word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览



文档简介
2020-2021年度北师大版八年级数学下册《1.3线段的垂直平分线》同步提升训练(附答案)
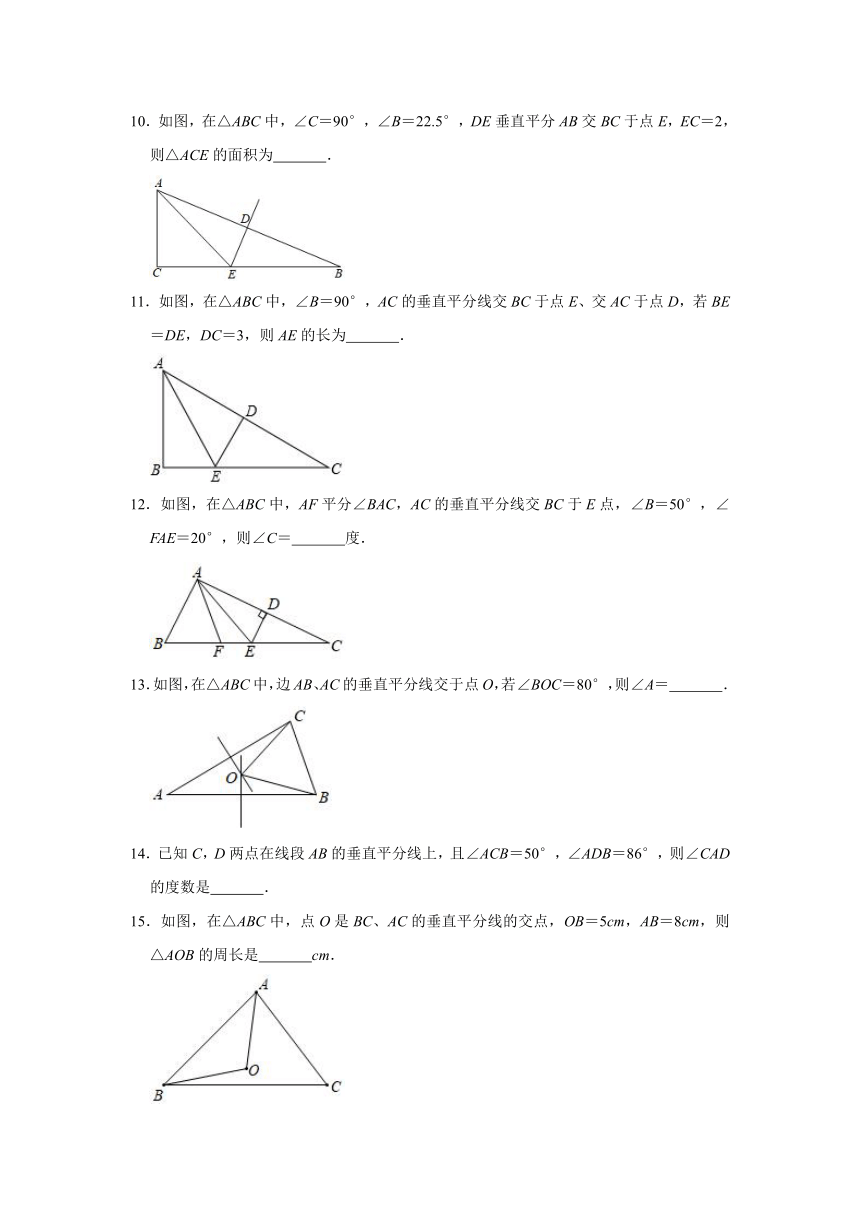
1.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在( )
A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点
D.AB的垂直平分线上
2.如图,在△ABC中,AI平分∠BAC,BI平分∠ABC,点O是AC、BC的垂直平分线的交点,连接AO、BO,若∠AIB=α,则∠AOB的大小为( )
A.α
B.4α﹣360°
C.α+90°
D.180°﹣α
3.如图,在△ABC中,BC=8,AB垂直平分线交AB于点M,交AC于点D,△BDC的周长为18,则AC为( )
A.10
B.16
C.18
D.26
4.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=4cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
5.如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为( )
A.40°
B.50°
C.80°
D.100°
6.A、B、C三个小区在一个三角形的三个顶点的位置上,要求在它们中间建造一座公园,为使三个小区到公园距离相等,则公园最适当的建造位置是在△ABC的( )
A.三条中线的交点
B.三条垂直平分线的交点
C.三条角平分线的交点
D.三边上高的交点
7.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为
.
8.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=
°.
9.如图,点O是△ABC内的一点,且点O到顶点A、B、C的距离相等,连接OB,OC,若∠A=78°,则∠BOC的度数为
.
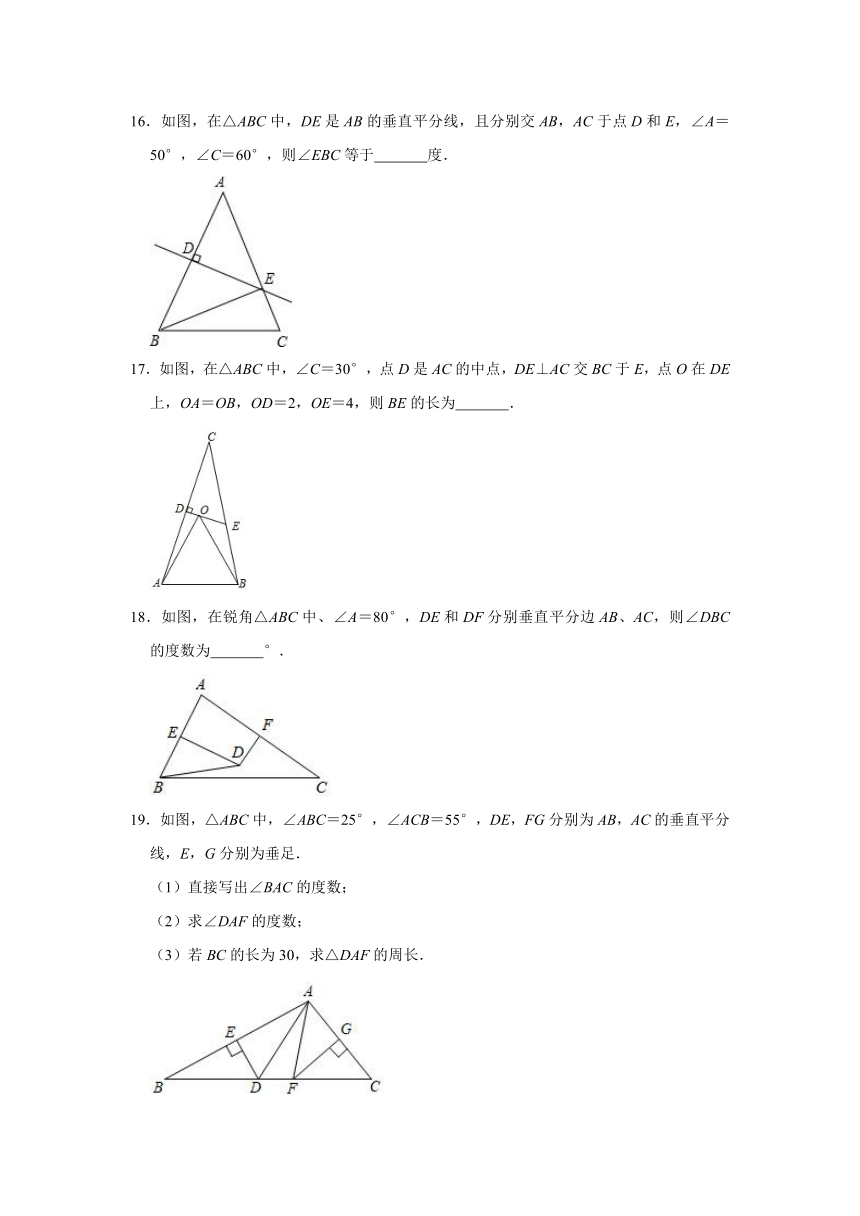
10.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为
.
11.如图,在△ABC中,∠B=90°,AC的垂直平分线交BC于点E、交AC于点D,若BE=DE,DC=3,则AE的长为
.
12.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C=
度.
13.如图,在△ABC中,边AB、AC的垂直平分线交于点O,若∠BOC=80°,则∠A=
.
14.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是
.
15.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是
cm.
16.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D和E,∠A=50°,∠C=60°,则∠EBC等于
度.
17.如图,在△ABC中,∠C=30°,点D是AC的中点,DE⊥AC交BC于E,点O在DE上,OA=OB,OD=2,OE=4,则BE的长为
.
18.如图,在锐角△ABC中、∠A=80°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为
°.
19.如图,△ABC中,∠ABC=25°,∠ACB=55°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数;
(3)若BC的长为30,求△DAF的周长.
20.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
21.如图,在四边形ABCD中,点E是边BC的中点,点F是边CD的中点,且AE⊥BC,AF⊥CD.
(1)求证:AB=AD;
(2)若∠BCD=114°,求∠BAD的度数.
22.如图,AD为△ABC的角平分线,DE⊥AB于点
E,DF⊥AC于点F,连接EF交AD于点O.
(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,写出DO与AD之间的数量关系,不需证明.
23.如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
24.如图,线段AB、AC的垂直平分线相交于D,连接BD、CD,若∠EDG=40°,求∠BDC的度数.
25.已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥∥BC,BM是线段CF的垂直平分线,垂足为M,N是线段BM上的一点,且NC=EF.
(1)若∠BNC=150°,EF=4,求FM的值.
(2)若BN=BE,求证:∠MNC=3∠MBC.
26.如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
参考答案
1.解:∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,
故选:A.
2.解:连接CO并延长至D,
∵∠AIB=α,
∴∠IAB+∠IBA=180°﹣α,
∵AI平分∠BAC,BI平分∠ABC,
∴∠IAB=∠CAB,∠IBA=∠CBA,
∴∠CAB+∠CBA=2(∠IAB+∠IBA)=360°﹣2α,
∴∠ACB=180°﹣(∠CAB+∠CBA)=2α﹣180°,
∵点O是AC、BC的垂直平分线的交点,
∴OA=OC,OB=OC,
∴∠OCA=∠OAC,∠OCB=∠OBC,
∵∠AOD是△AOC的一个外角,
∴∠AOD=∠OCA+∠OAC=2∠OCA,
同理,∠BOD=2∠OCB,
∴∠AOB=∠AOD+∠BOD=2∠OCA+2∠OCB=4α﹣360°,
故选:B.
3.解:∵MN是AB的垂直平分线,
∴DA=DB,
∵△BDC的周长为18,
∴BC+CD+BD=BC+CD+AD=BC+AC=18,
∵BC=8,
∴AC=10,
故选:A.
4.解:∵DE是AB的垂直平分线,
∴DB=DA,AB=2AE=8(cm),
∵△ADC的周长为9cm,
∴AC+CD+DA=AC+CD+DB=AC+BC=9(cm),
∴△ABC的周长=AC+BC+AB=17(cm),
故选:D.
5.解:∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=40°,
∴∠BEC=∠EBA+∠A=80°,
故选:C.
6.解:∵线段的垂直平分线上的点到线段的两个端点的距离相等,
∴三个小区到公园距离相等,公园最适当的建造位置是在△ABC三边垂直平分线上,
故选:B.
7.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=11,
故答案为:11.
8.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
9.解:连接OA,
∵∠BCA=78°,
∴∠ABC+∠ACB=180°﹣78°=102°,
∵OA=OB,
∴∠OBA=∠OAB,
同理,∠OCA=∠OAC,
∴∠OBA+∠OCA=∠OAB+∠OAC=78°,
∴∠OBC+∠OCB=102°﹣78°=24°,
∴∠BOC=180°﹣24°=156°,
故答案为:156°.
10.解:∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=22.5°,
∴∠AEC=∠EAB+∠B=45°,
∴AC=EC=2,
∴△ACE的面积=×AC×EC=×2×2=2,
故答案为:2.
11.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵BE=DE,∠B=90°,ED⊥AC,
∴∠EAC=∠BAE,
∴∠EAC=∠C=∠BAE=30°,
在Rt△CED中,EC==2,
∴AE=2,
故答案为:2.
12.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°,
故答案为:30.
13.解:连接OA,
∵∠BOC=80°,
∴∠OBC+∠OCB=100°,
∴∠OAB+∠OBA+∠OAC+∠OCA=80°,
∵AB、AC的垂直平分线交于点O,
∴AO=BO,AO=CO,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠A=∠OAB+∠OAC=40°,
故答案为:40°.
14.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
15.解:∵点O是BC、AC的垂直平分线的交点,
∴OA=OB=5cm,
∴△AOB的周长=OA+OB+AB=18(cm),
故答案为:18.
16.解:∵A=50°,∠C=60°,
∴∠ABC=180°﹣50°﹣60°=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=50°,
∴∠EBC=∠ABC﹣∠EBA=70°﹣50°=20°,
故答案为:20.
17.解:连接OC,作OF⊥BC于点F,
由题意得,DE=OD+OE=6,
在Rt△CDE中,∠DCE=30°,
∴CE=2DE=12,∠OEF=60°,
∵AD=DC,ED⊥AC,
∴OA=OC,
∵OA=OB,
∴OB=OC,
∵OF⊥BC,
∴CF=FB,
在Rt△OFE中,∠OEF=60°,
∴∠EOF=30°,
∴EF=OE=2,
∴CF=CE﹣EF=10,
∴BC=20,
∴BE=20﹣12=8,
故答案为:8.
18.解:连接DA、DC,
∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵DE和DF分别垂直平分边AB、AC,
∴DA=DB,DA=DC,
∴DB=DC,∠DBA=∠DAB,∠DAC=∠DCA,
∴∠DBA+∠DCA=∠DAB+∠DAC=80°,
∴∠DBC=∠DBC=×(100°﹣80°)=10°,
故答案为:10.
19.解:(1)∵∠ABC=25°,∠ACB=55°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=100°;
(2)∵DE,FG分别为AB,AC的垂直平分线,
∴DA=DB,FA=FC,
∴∠DAB=∠ABC=25°,∠FAC=∠ACB=55°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=20°;
(3)△DAF的周长=DA+DF+FA=DB+DF+FC=BC=30.
20.(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为14cm,
∴AB+BC+AC=14(cm),
∵AC=6cm,
∴AB+BC=8(cm),
∵AB=EC,BD=DE,
∴DC=DE+EC=(AB+BC)=4(cm).
21.解:(1)连接AC,
∵点E是边BC的中点,AE⊥BC,
∴AB=AC(垂直平分线的性质)
同理AD=AC,
∴AB=AD;
(2)∵AB=AC,AD=AC,
∴∠B=∠1,∠D=∠2,
∴∠B+∠D=∠1+∠2,
即∠B+∠D=∠BCD,
∵∠BAD+(∠B+∠D)+∠BCD=(4﹣2)?180°=360°,∠BCD=114°,
∴∠BAD=360°﹣114°﹣114°=132°.
22.(1)证明:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A、D都在EF的垂直平分线上,
∴AD垂直平分EF;
(2),
证明:∵AD为△ABC的角平分线,∠BAC=60°,
∴∠EAD=30°,
∴DE=AD,
∵∠EAD=30°,DE⊥AB,
∴∠DEO=30°,
∴OD=DE,
∴DO=AD.
23.解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC﹣∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
在△ECD和△FCB中,
,
∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,
∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
24.解:经过点D作射线AH,
∵∠EDG=40°,
∴∠EDF=180°﹣40°=140°,
∵DF⊥AB,DE⊥AC,
∴∠BAC=180°﹣∠EDF=40°,
∵线段AB、AC的垂直平分线相交于D,
∴DA=DB,DA=DC,
∴∠DAB=∠DBA,∠DAC=∠DCA,
∴∠BDC=∠BDH+∠CDH=2∠DAB+2∠DAC=80°.
25.(1)解:如图1中,
∵∠BNC=150°,
∴∠CNM=30°,
∵BM垂直平分线段FC,
∴∠NMC=90°,FM=CM,
∵CN=EF=4,
∴CM=FM=CN=2.
(2)证明:如图2中,连接FN,BF.
∵BM垂直平分线段CF,
∴BF=BC,NC=NF,
∴∠CBN=∠FBN,
∵EF=NC,
∴EF=FN,∵BE=BN,BF=BF,
∴△BFE≌△BFN(SSS),
∴∠EFB=∠∠NFB,
∵EF∥BC,
∴∠EFB=∠FBC=2∠CBN,
∴∠BFN=2∠CBN,
∵∠CNM=∠MNF=∠NBF+∠BFN,
∴∠CNM=3∠MBC.
26.解:∠CAF=∠B.
理由如下:∵EF垂直平分AD
∴FA=FD,
∴∠FAD=∠FDA,
∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∴∠CAF=∠B.
1.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在( )
A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点
D.AB的垂直平分线上
2.如图,在△ABC中,AI平分∠BAC,BI平分∠ABC,点O是AC、BC的垂直平分线的交点,连接AO、BO,若∠AIB=α,则∠AOB的大小为( )
A.α
B.4α﹣360°
C.α+90°
D.180°﹣α
3.如图,在△ABC中,BC=8,AB垂直平分线交AB于点M,交AC于点D,△BDC的周长为18,则AC为( )
A.10
B.16
C.18
D.26
4.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=4cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
5.如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为( )
A.40°
B.50°
C.80°
D.100°
6.A、B、C三个小区在一个三角形的三个顶点的位置上,要求在它们中间建造一座公园,为使三个小区到公园距离相等,则公园最适当的建造位置是在△ABC的( )
A.三条中线的交点
B.三条垂直平分线的交点
C.三条角平分线的交点
D.三边上高的交点
7.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为
.
8.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=
°.
9.如图,点O是△ABC内的一点,且点O到顶点A、B、C的距离相等,连接OB,OC,若∠A=78°,则∠BOC的度数为
.
10.如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于点E,EC=2,则△ACE的面积为
.
11.如图,在△ABC中,∠B=90°,AC的垂直平分线交BC于点E、交AC于点D,若BE=DE,DC=3,则AE的长为
.
12.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C=
度.
13.如图,在△ABC中,边AB、AC的垂直平分线交于点O,若∠BOC=80°,则∠A=
.
14.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是
.
15.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是
cm.
16.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D和E,∠A=50°,∠C=60°,则∠EBC等于
度.
17.如图,在△ABC中,∠C=30°,点D是AC的中点,DE⊥AC交BC于E,点O在DE上,OA=OB,OD=2,OE=4,则BE的长为
.
18.如图,在锐角△ABC中、∠A=80°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为
°.
19.如图,△ABC中,∠ABC=25°,∠ACB=55°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数;
(3)若BC的长为30,求△DAF的周长.
20.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
21.如图,在四边形ABCD中,点E是边BC的中点,点F是边CD的中点,且AE⊥BC,AF⊥CD.
(1)求证:AB=AD;
(2)若∠BCD=114°,求∠BAD的度数.
22.如图,AD为△ABC的角平分线,DE⊥AB于点
E,DF⊥AC于点F,连接EF交AD于点O.
(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,写出DO与AD之间的数量关系,不需证明.
23.如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
24.如图,线段AB、AC的垂直平分线相交于D,连接BD、CD,若∠EDG=40°,求∠BDC的度数.
25.已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥∥BC,BM是线段CF的垂直平分线,垂足为M,N是线段BM上的一点,且NC=EF.
(1)若∠BNC=150°,EF=4,求FM的值.
(2)若BN=BE,求证:∠MNC=3∠MBC.
26.如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
参考答案
1.解:∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,
故选:A.
2.解:连接CO并延长至D,
∵∠AIB=α,
∴∠IAB+∠IBA=180°﹣α,
∵AI平分∠BAC,BI平分∠ABC,
∴∠IAB=∠CAB,∠IBA=∠CBA,
∴∠CAB+∠CBA=2(∠IAB+∠IBA)=360°﹣2α,
∴∠ACB=180°﹣(∠CAB+∠CBA)=2α﹣180°,
∵点O是AC、BC的垂直平分线的交点,
∴OA=OC,OB=OC,
∴∠OCA=∠OAC,∠OCB=∠OBC,
∵∠AOD是△AOC的一个外角,
∴∠AOD=∠OCA+∠OAC=2∠OCA,
同理,∠BOD=2∠OCB,
∴∠AOB=∠AOD+∠BOD=2∠OCA+2∠OCB=4α﹣360°,
故选:B.
3.解:∵MN是AB的垂直平分线,
∴DA=DB,
∵△BDC的周长为18,
∴BC+CD+BD=BC+CD+AD=BC+AC=18,
∵BC=8,
∴AC=10,
故选:A.
4.解:∵DE是AB的垂直平分线,
∴DB=DA,AB=2AE=8(cm),
∵△ADC的周长为9cm,
∴AC+CD+DA=AC+CD+DB=AC+BC=9(cm),
∴△ABC的周长=AC+BC+AB=17(cm),
故选:D.
5.解:∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=40°,
∴∠BEC=∠EBA+∠A=80°,
故选:C.
6.解:∵线段的垂直平分线上的点到线段的两个端点的距离相等,
∴三个小区到公园距离相等,公园最适当的建造位置是在△ABC三边垂直平分线上,
故选:B.
7.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=11,
故答案为:11.
8.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
9.解:连接OA,
∵∠BCA=78°,
∴∠ABC+∠ACB=180°﹣78°=102°,
∵OA=OB,
∴∠OBA=∠OAB,
同理,∠OCA=∠OAC,
∴∠OBA+∠OCA=∠OAB+∠OAC=78°,
∴∠OBC+∠OCB=102°﹣78°=24°,
∴∠BOC=180°﹣24°=156°,
故答案为:156°.
10.解:∵DE垂直平分AB,
∴EA=EB,
∴∠EAB=∠B=22.5°,
∴∠AEC=∠EAB+∠B=45°,
∴AC=EC=2,
∴△ACE的面积=×AC×EC=×2×2=2,
故答案为:2.
11.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵BE=DE,∠B=90°,ED⊥AC,
∴∠EAC=∠BAE,
∴∠EAC=∠C=∠BAE=30°,
在Rt△CED中,EC==2,
∴AE=2,
故答案为:2.
12.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°,
故答案为:30.
13.解:连接OA,
∵∠BOC=80°,
∴∠OBC+∠OCB=100°,
∴∠OAB+∠OBA+∠OAC+∠OCA=80°,
∵AB、AC的垂直平分线交于点O,
∴AO=BO,AO=CO,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠A=∠OAB+∠OAC=40°,
故答案为:40°.
14.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
15.解:∵点O是BC、AC的垂直平分线的交点,
∴OA=OB=5cm,
∴△AOB的周长=OA+OB+AB=18(cm),
故答案为:18.
16.解:∵A=50°,∠C=60°,
∴∠ABC=180°﹣50°﹣60°=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=50°,
∴∠EBC=∠ABC﹣∠EBA=70°﹣50°=20°,
故答案为:20.
17.解:连接OC,作OF⊥BC于点F,
由题意得,DE=OD+OE=6,
在Rt△CDE中,∠DCE=30°,
∴CE=2DE=12,∠OEF=60°,
∵AD=DC,ED⊥AC,
∴OA=OC,
∵OA=OB,
∴OB=OC,
∵OF⊥BC,
∴CF=FB,
在Rt△OFE中,∠OEF=60°,
∴∠EOF=30°,
∴EF=OE=2,
∴CF=CE﹣EF=10,
∴BC=20,
∴BE=20﹣12=8,
故答案为:8.
18.解:连接DA、DC,
∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵DE和DF分别垂直平分边AB、AC,
∴DA=DB,DA=DC,
∴DB=DC,∠DBA=∠DAB,∠DAC=∠DCA,
∴∠DBA+∠DCA=∠DAB+∠DAC=80°,
∴∠DBC=∠DBC=×(100°﹣80°)=10°,
故答案为:10.
19.解:(1)∵∠ABC=25°,∠ACB=55°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=100°;
(2)∵DE,FG分别为AB,AC的垂直平分线,
∴DA=DB,FA=FC,
∴∠DAB=∠ABC=25°,∠FAC=∠ACB=55°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=20°;
(3)△DAF的周长=DA+DF+FA=DB+DF+FC=BC=30.
20.(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为14cm,
∴AB+BC+AC=14(cm),
∵AC=6cm,
∴AB+BC=8(cm),
∵AB=EC,BD=DE,
∴DC=DE+EC=(AB+BC)=4(cm).
21.解:(1)连接AC,
∵点E是边BC的中点,AE⊥BC,
∴AB=AC(垂直平分线的性质)
同理AD=AC,
∴AB=AD;
(2)∵AB=AC,AD=AC,
∴∠B=∠1,∠D=∠2,
∴∠B+∠D=∠1+∠2,
即∠B+∠D=∠BCD,
∵∠BAD+(∠B+∠D)+∠BCD=(4﹣2)?180°=360°,∠BCD=114°,
∴∠BAD=360°﹣114°﹣114°=132°.
22.(1)证明:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A、D都在EF的垂直平分线上,
∴AD垂直平分EF;
(2),
证明:∵AD为△ABC的角平分线,∠BAC=60°,
∴∠EAD=30°,
∴DE=AD,
∵∠EAD=30°,DE⊥AB,
∴∠DEO=30°,
∴OD=DE,
∴DO=AD.
23.解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC﹣∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
在△ECD和△FCB中,
,
∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,
∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
24.解:经过点D作射线AH,
∵∠EDG=40°,
∴∠EDF=180°﹣40°=140°,
∵DF⊥AB,DE⊥AC,
∴∠BAC=180°﹣∠EDF=40°,
∵线段AB、AC的垂直平分线相交于D,
∴DA=DB,DA=DC,
∴∠DAB=∠DBA,∠DAC=∠DCA,
∴∠BDC=∠BDH+∠CDH=2∠DAB+2∠DAC=80°.
25.(1)解:如图1中,
∵∠BNC=150°,
∴∠CNM=30°,
∵BM垂直平分线段FC,
∴∠NMC=90°,FM=CM,
∵CN=EF=4,
∴CM=FM=CN=2.
(2)证明:如图2中,连接FN,BF.
∵BM垂直平分线段CF,
∴BF=BC,NC=NF,
∴∠CBN=∠FBN,
∵EF=NC,
∴EF=FN,∵BE=BN,BF=BF,
∴△BFE≌△BFN(SSS),
∴∠EFB=∠∠NFB,
∵EF∥BC,
∴∠EFB=∠FBC=2∠CBN,
∴∠BFN=2∠CBN,
∵∠CNM=∠MNF=∠NBF+∠BFN,
∴∠CNM=3∠MBC.
26.解:∠CAF=∠B.
理由如下:∵EF垂直平分AD
∴FA=FD,
∴∠FAD=∠FDA,
∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∴∠CAF=∠B.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
