3.4等式的基本性质课件

(共49张PPT)
音乐能激发或抚慰情怀，
绘画使人赏心悦目，
诗歌能动人心弦，
哲学使人获得智慧，
科学可改善物质生活，
但数学能给予以上的一切，
数学是人类最完美的语言。
数学的魅力
等式的性质
初一（一）班
能否用估算法求出下列方程的解
(2) 2x +5= 21
(1) x+2=12
算一算试试

试一试
(3) 23x=230
(4) 2500+900x = 15000
方程是含有未知数的等式，为了讨论解方程，我们先来看看等式有什么性质．
请问，什么是等式？
方程(1)(3)的解可以观察得到,但是仅靠观察来解比较复杂的方程(2)(4)就比较困难.因此,我们还要讨论怎样解方程．
像这样用等号“=”表示相等关系的式子叫等式．
　在等式中，等号左（右）边的式子叫做这个等式的左（右）边．
知识
准备
什么是等式？
举个例子？
⑦ 1+2=3, ⑧ ab, ⑨ S= ab,
⑩ 2x-3y
①4+x=7， ② 2x<5, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2　 ⑥ L=2πr
2
3
1
2
上述这组式子中，( 　　 )是等式， 　(　　　　　　 ) 不是等式，为什么？
①④⑥⑦⑨
②③⑤⑧⑩
随
练一练
那么刚刚我们估算的那些方程如何解的？
是否正确？
下面就让我们一起来讨论等式的性质吧！
a
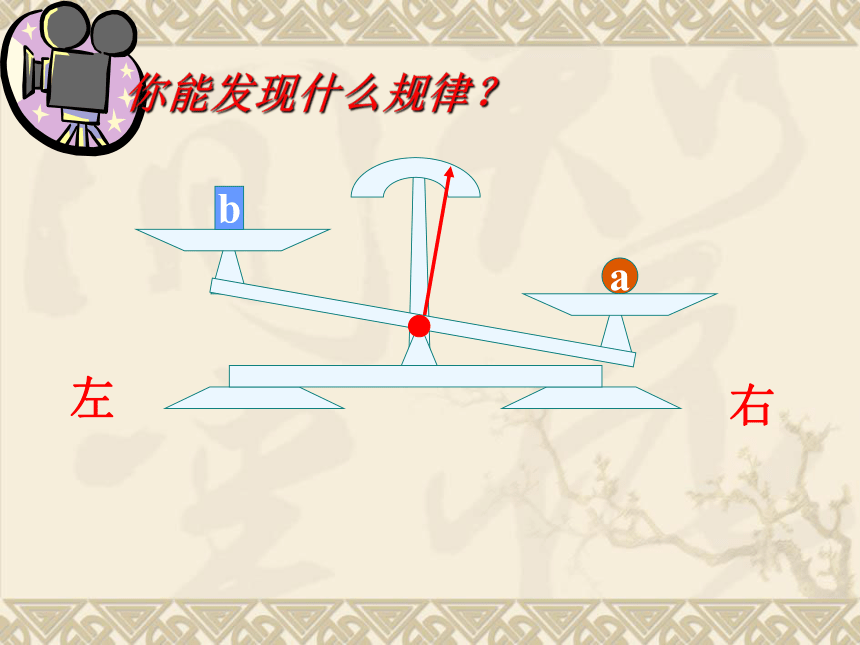
你能发现什么规律？
右
左
a
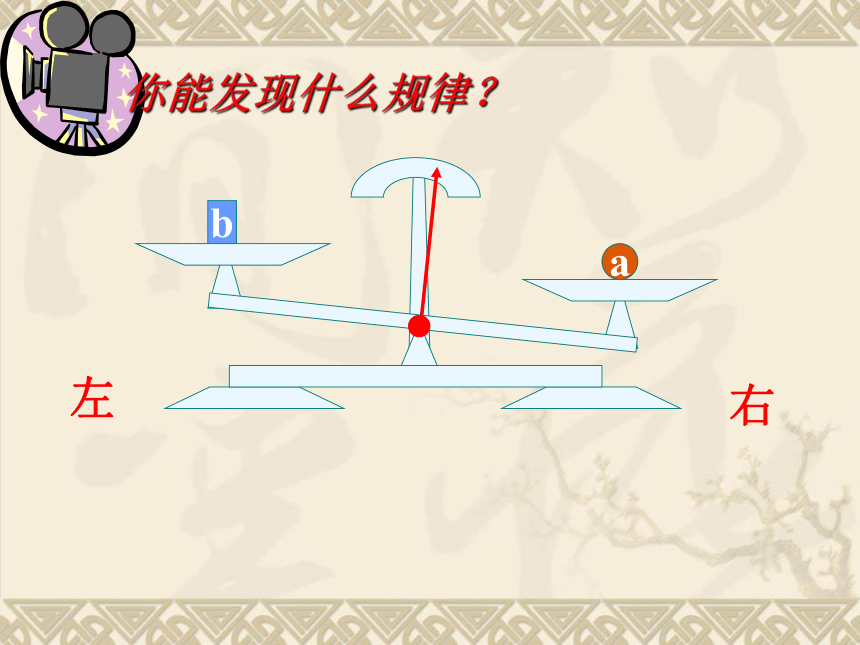
你能发现什么规律？
右
左
a
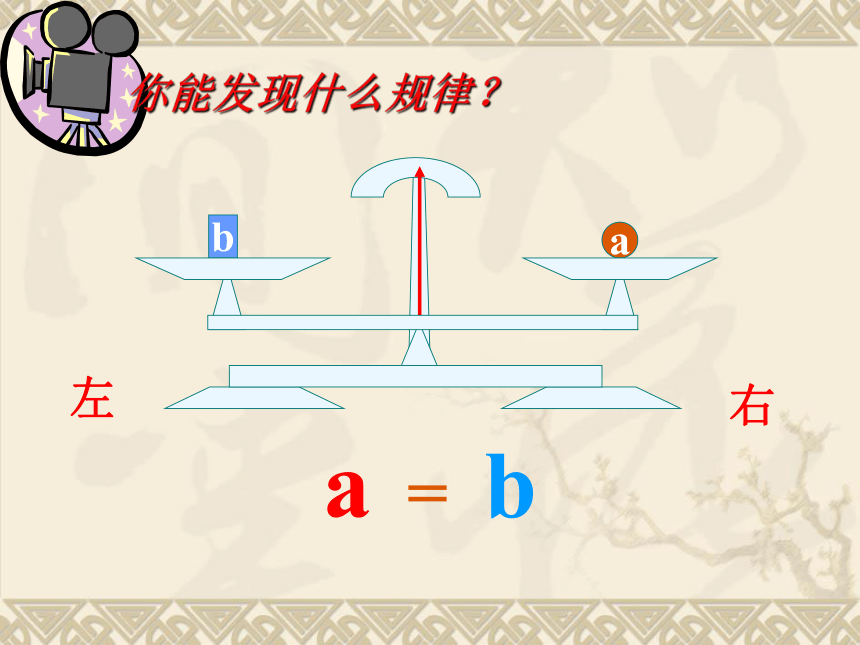
你能发现什么规律？
右
左
a
b
你能发现什么规律？
右
左
b
a
你能发现什么规律？
右
左
b
a
你能发现什么规律？
a = b
右
左
b
a
你能发现什么规律？
a = b
c
右
左
c
b
a
你能发现什么规律？
a = b
右
左
a
c
b
你能发现什么规律？
a = b
右
左
c
b
c
a
你能发现什么规律？
a = b
右
左
c
b
c
a
你能发现什么规律？
a = b
a+c b+c
=
右
左
c
c
你能发现什么规律？
a = b
a
b
右
左
c
你能发现什么规律？
a = b
a
b
右
左
c
你能发现什么规律？
a = b
a
b
右
左
你能发现什么规律？
a = b
b
a
右
左
你能发现什么规律？
a = b
a-c b-c
=
b
a
右
左
等式的性质１：等式的两边加（或减）同一个数（或式子），结果仍相等．
性质１用式子可表示为：如果a=b ， 那么　　　　　　　a±c=b±c
在下面的括号内填上适当的数或者式子：
（1）因为：
所以：
（2）因为：
所以：
想一想、练一练
b
a
你能发现什么规律？
a = b
右
左
b
a
你能发现什么规律？
a = b
右
左
a
b
2a = 2b
b
a
你能发现什么规律？
a = b
右
左
b
b
a
a
3a = 3b
b
a
你能发现什么规律？
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
b
a
你能发现什么规律？
a = b
右
左
等式的性质２：等式的两边乘同一个数，或除以同一个不为０的数，结果仍相等．
性质２用式子可表示为：
如果a=b， 那么　ac=bc
如果a=b ，那么
等式的性质
性质1: 等式两边加(或减)同一个数(或式子), 结果仍相等.
性质2: 等式两边乘同一个数, 或除以同一个不为０的数, 结果仍相等.
注意：（１）等式两边都要参加运算，且是同一种运算．
（２）等式两边加或减，乘或除以的数一定是同一个数或同一个式子．
（３）等式两边不能都除以０，即０不能作除数或分母．
×
√
×
×
√
(1)如果x=y,那么 （ ）
(2)如果x=y,那么 （ ）
(3)如果x=y,那么 （ ）
(4)如果x=y,那么 （ ）
(5)如果x=y,那么 （ ）
判断对错，对的说明根据等式的哪一条性质；错的说出为什么。
3
2
y
3
2
x
+
=
-
a
5
y
a
5
x
-
+
=
-
+
a
5
y
a
5
x
-
=
-
y
5
x
5
=
-
3
1
y
2
3
1
x
2
-
=
-
用适当的数或整式填空，使得结果仍是等式，并说明依据是什么。
利用等式的性质解下列方程
解：两边减7，得
于是
解：两边除以-5，得
于是
分析：所谓“解方程”就是要求出方程的解“x＝？”因此我们需要把方程转化为“x＝a（a为常数）”的形式．
解：两边加5，得
化简，得
两边同乘-3，得
检验：
将
代入方程
，得：
左边
右边
所以
是方程
的解。
解：两边加5，得
化简，得
两边同乘-3，得
解：两边同乘-3，得
化简，得
两边同减15，得
解法一：
解法二：
随
练一练
两边同时除以5，得
两边同时减2，得
两边同时乘2，得
两边同除以0.3，得
(1)解：
8
=
x
两边同时减4，得
(2)解：
(3)解：
记得检验！
经过对原方程的一系列变形(两边同加减、乘除)，最终把方程化为最简的等式：
x = a(常数）
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
1.下列说法错误的是（ ）.
C
随
练一练
2.下列各式变形正确的是（ ）.
A
随
练一练
3.等式 的下列变形，利用等式性质2进行变形的是（ ）.
D
随
练一练
－、填空
(1)如果x-3=6，那么x = 　　 ，
依据　　　　　　　　　；
(2)如果2x=x－1，那么x = ，
依据　　　　　　　　 ；
(3)如果-5x=20 ，那么x＝　　，
依据　　　　　　　　 。
(4)如果－　 ｘ＝８，那么ｘ＝　　 ，
依据　　　　　　　 ；
快乐练习
９
等式的性质１　
等式的性质１　
－１
－10
－4
等式的性质２　
等式的性质２　
变形为
变形为
变形为
变形为
二、选择填空
下列各式的变形中，正确的是（　）
快乐练习
A.
C.
D.
B.
D
太棒了!
(2)如果 ，那么下列等式中不一定成立
的是（ ）
快乐练习
A.
C.
D.
B.
好极了!
D
能力提升
若 请根据等式性质编出三个等式，并说出你编写的依据。
×
( )
（1）
(2)
(3)
( )
( )
√
√
√
判断下列说法是否成立，并说明理由
（　　）
（　　）
（　　）
.
（因为x可能等于0）
（等量代换）
（等式的性质）
等式的性质
1: 等式两边加(或减)同一个数(或式子)，结果仍相等。
如果 a=b
那么a + c=b + c
掌握关键:<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
解方程的目标: 变形 x = a (常数)
检验的方程
(代 入)
原方程
2: 等式两边乘同一个数或除以同一个不为0的数,结果仍相等。
如果 a=b 那么 ac = bc
如果 a=b 那么
解下列方程：
⑴　x+2=-6
⑵　-3x=3-4x
⑶
⑷　-6x=2
练一练
判断以下计算过程是否正确：
把等式x2=2x变形
解：由等式性质2，两边同除以x，得
　　　　　　＝
于是 x=2　
x2
x
x
2x
作业：