苏教版六年级下册数学反比例的意义同步练习(含答案)
文档属性
| 名称 | 苏教版六年级下册数学反比例的意义同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 145.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览

文档简介
例3反比例的意义
知识回顾:
1.
2. x×y=k(一定) x和y成反比例
[基础巩固]
一、填空。
1.如果=(和不为0),那么和成( );
如果=(和不为0)那么和成( );
如果=3(和不为0)那么和成( )。
2.用36元购买土豆,购买的单价和数量的情况如下表。
(1)购买土豆的数量随着单价的变化而变化,土豆的单价越高,购买的数量就越( ),土豆的单价越低,购买土豆的数量就越( )。
(2) 可以用式子( )表示总价、单价、数量之间的关系。土豆的单价和购买的数量成( )比例关系。土豆的单价和购买的数量 是成( )的量。
(3)如果土豆的单价是2.5元,那么可以买( )千克。
3.
当和成正比例时,是( );
当和成反比例时,是( )。
二、判断下面各题中的两种量成什么比例。
1.图上距离一定,实际距离和比例尺。( )
2.圆锥的高一定,它的体积和底面积。( )
3.每台电脑价格一定,购买的台数和总价。( )
4.长方形的周长一定,它的长与宽。( )
5.三角形的面积一定,它的底与高。( )
6.分子一定,分母和分数值。( )
7.圆的直径一定,周长和圆周率。( )
8.小明的体重和年龄。( )
[拓展提高]
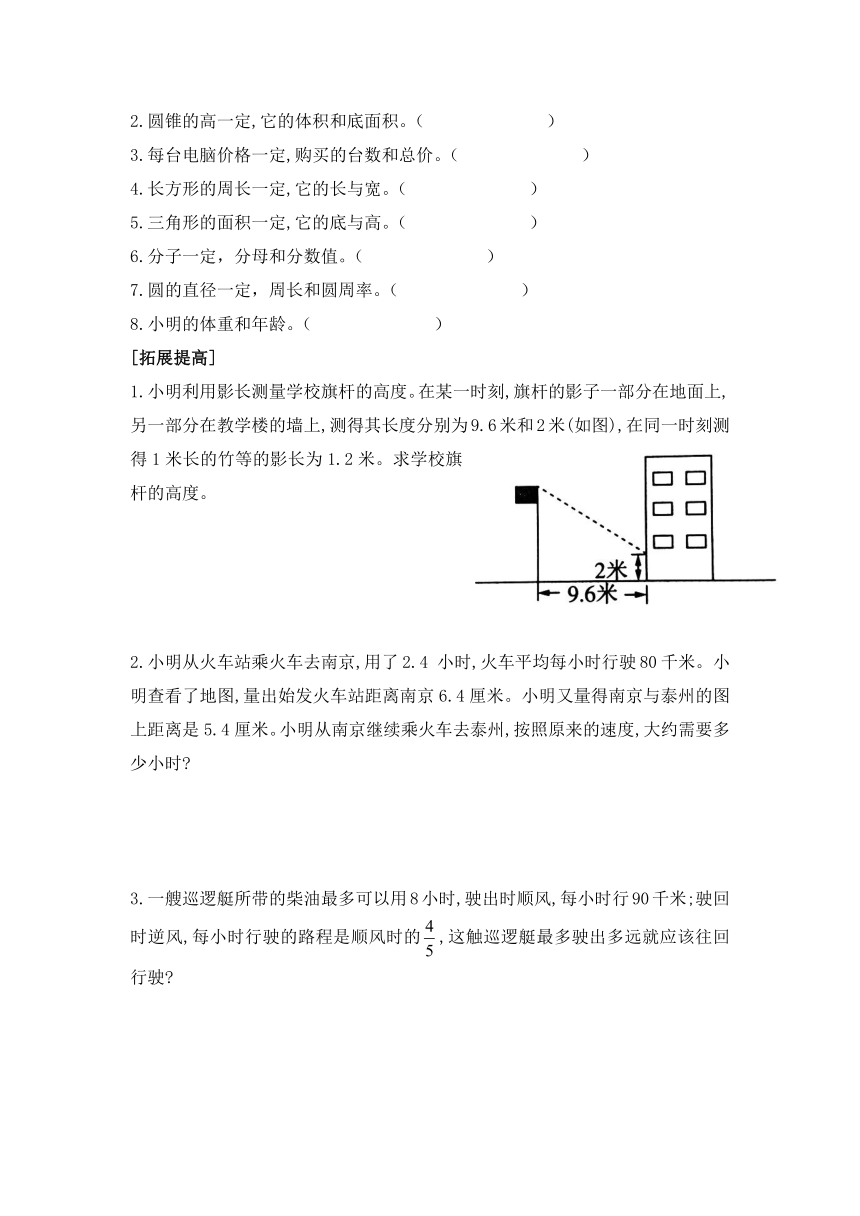
1.小明利用影长测量学校旗杆的高度。在某一时刻,旗杆的影子一部分在地面上,另一部分在教学楼的墙上,测得其长度分别为9.6米和2米(如图),在同一时刻测得1米长的竹等的影长为1.2米。求学校旗杆的高度。
2.小明从火车站乘火车去南京,用了2.4 小时,火车平均每小时行驶80千米。 小明查看了地图,量出始发火车站距离南京6.4厘米。小明又量得南京与泰州的图上距离是5.4厘米。小明从南京继续乘火车去泰州,按照原来的速度,大约需要多少小时?
3.一艘巡逻艇所带的柴油最多可以用8小时,驶出时顺风,每小时行90千米;驶回时逆风,每小时行驶的路程是顺风时的,这触巡逻艇最多驶出多远就应该往回行驶?
4.小明家新买了一辆家用小轿车,其油箱可装油40升,小轿车行驶后,油箱中剩余油量与 行驶时间的关系如图。
(1)一箱油够连续行驶( )小时。
(2)耗油量与行驶时间成正比例吗?为什么?
5.如图,在三角形ABC中,AD垂直于BC,BE垂直于AC,AD=4厘米,BE=5厘米,AC+BC=10.8厘米。求三角形ABC的面积。
6.图书馆买回一批新书,分别放在甲、乙两个书架上,甲书架放了这批书的55%,如果从 甲书架拿出150本书放到乙书架,那么甲、乙两书架所放新书的比是2:3。这批新书共有多少本?
答案
一、填空。
1. 成比例 正比例 反比例
2. (1) 少 多
(2)单价×数量=总价 反 反比例
(3)14.4
3. 100 25
二、判断下面各题中的两种量成什么比例。
1. 反比例
2. 正比例
3. 正比例
4. 不成比例
5. 反比例
6. 反比例
7. 不成比例
8. 不成比例
[拓展提高]
1. 10米
2. 2.025
3.
4. (1)8
(2)成正比例,因为耗油量÷行驶时间=每小时耗油量(一定)
5. 12平方厘米
6. 1000
知识回顾:
1.
2. x×y=k(一定) x和y成反比例
[基础巩固]
一、填空。
1.如果=(和不为0),那么和成( );
如果=(和不为0)那么和成( );
如果=3(和不为0)那么和成( )。
2.用36元购买土豆,购买的单价和数量的情况如下表。
(1)购买土豆的数量随着单价的变化而变化,土豆的单价越高,购买的数量就越( ),土豆的单价越低,购买土豆的数量就越( )。
(2) 可以用式子( )表示总价、单价、数量之间的关系。土豆的单价和购买的数量成( )比例关系。土豆的单价和购买的数量 是成( )的量。
(3)如果土豆的单价是2.5元,那么可以买( )千克。
3.
当和成正比例时,是( );
当和成反比例时,是( )。
二、判断下面各题中的两种量成什么比例。
1.图上距离一定,实际距离和比例尺。( )
2.圆锥的高一定,它的体积和底面积。( )
3.每台电脑价格一定,购买的台数和总价。( )
4.长方形的周长一定,它的长与宽。( )
5.三角形的面积一定,它的底与高。( )
6.分子一定,分母和分数值。( )
7.圆的直径一定,周长和圆周率。( )
8.小明的体重和年龄。( )
[拓展提高]
1.小明利用影长测量学校旗杆的高度。在某一时刻,旗杆的影子一部分在地面上,另一部分在教学楼的墙上,测得其长度分别为9.6米和2米(如图),在同一时刻测得1米长的竹等的影长为1.2米。求学校旗杆的高度。
2.小明从火车站乘火车去南京,用了2.4 小时,火车平均每小时行驶80千米。 小明查看了地图,量出始发火车站距离南京6.4厘米。小明又量得南京与泰州的图上距离是5.4厘米。小明从南京继续乘火车去泰州,按照原来的速度,大约需要多少小时?
3.一艘巡逻艇所带的柴油最多可以用8小时,驶出时顺风,每小时行90千米;驶回时逆风,每小时行驶的路程是顺风时的,这触巡逻艇最多驶出多远就应该往回行驶?
4.小明家新买了一辆家用小轿车,其油箱可装油40升,小轿车行驶后,油箱中剩余油量与 行驶时间的关系如图。
(1)一箱油够连续行驶( )小时。
(2)耗油量与行驶时间成正比例吗?为什么?
5.如图,在三角形ABC中,AD垂直于BC,BE垂直于AC,AD=4厘米,BE=5厘米,AC+BC=10.8厘米。求三角形ABC的面积。
6.图书馆买回一批新书,分别放在甲、乙两个书架上,甲书架放了这批书的55%,如果从 甲书架拿出150本书放到乙书架,那么甲、乙两书架所放新书的比是2:3。这批新书共有多少本?
答案
一、填空。
1. 成比例 正比例 反比例
2. (1) 少 多
(2)单价×数量=总价 反 反比例
(3)14.4
3. 100 25
二、判断下面各题中的两种量成什么比例。
1. 反比例
2. 正比例
3. 正比例
4. 不成比例
5. 反比例
6. 反比例
7. 不成比例
8. 不成比例
[拓展提高]
1. 10米
2. 2.025
3.
4. (1)8
(2)成正比例,因为耗油量÷行驶时间=每小时耗油量(一定)
5. 12平方厘米
6. 1000
