2020-2021学年 北师大版八年级数学下册第三章 图形的平移与旋转 章末测试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年 北师大版八年级数学下册第三章 图形的平移与旋转 章末测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 372.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 14:12:46 | ||
图片预览

文档简介
第三章
图形的平移与旋转
一、选择题(每小题3分,共30分)
1.如图所示的图案中,为中心对称图形的是(??)
A.①② ??B.②③
C.②④ ??D.③④
2.下列四个图案中,不能由1号图形平移得到2号图形的是( )
3.观察图中的三个图形,照此规律,可知第四个图形是( )
4.如图,小聪坐在秋千上旋转了80°,其位置从P点运动到了P'点,则∠OPP'的度数为( )
A.40° ??B.50°
C.70° ??D.80°
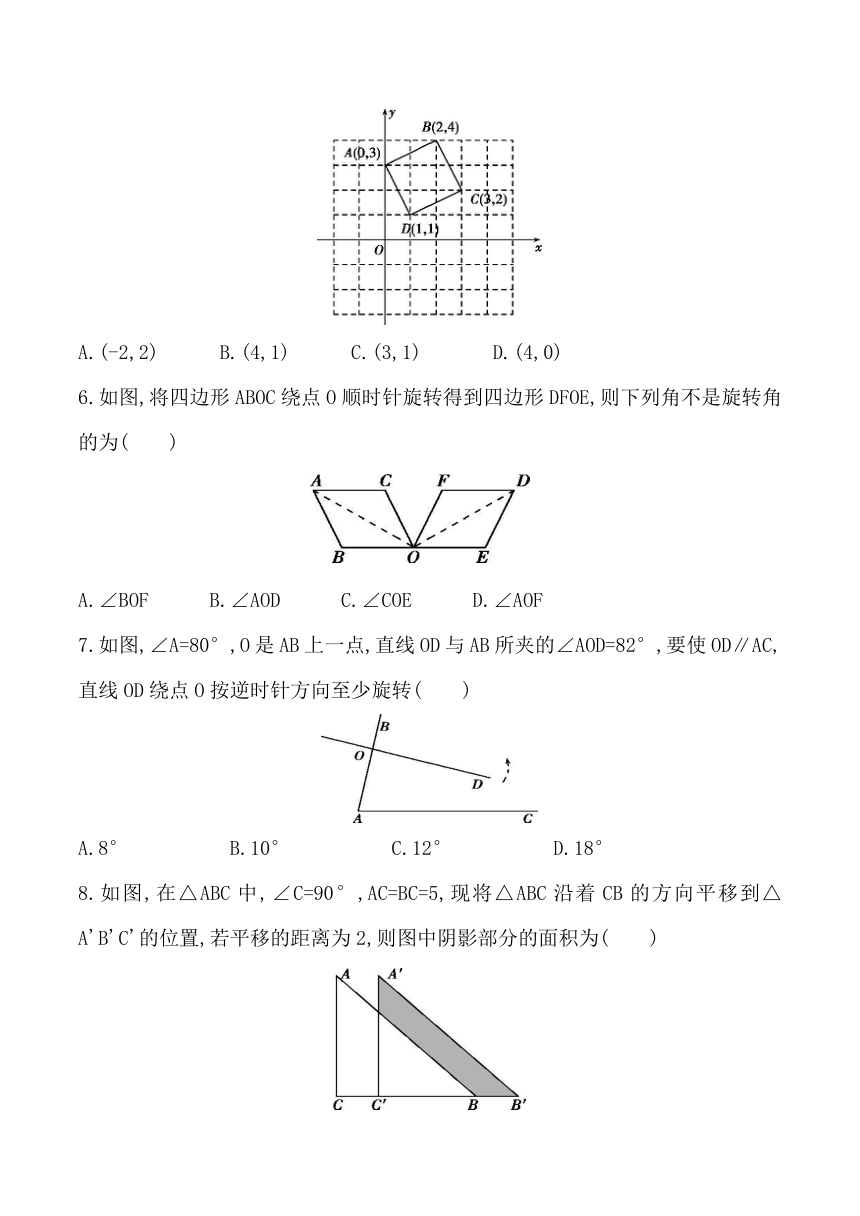
5.如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为(??)
A.(-2,2) ??B.(4,1)
C.(3,1)
??D.(4,0)
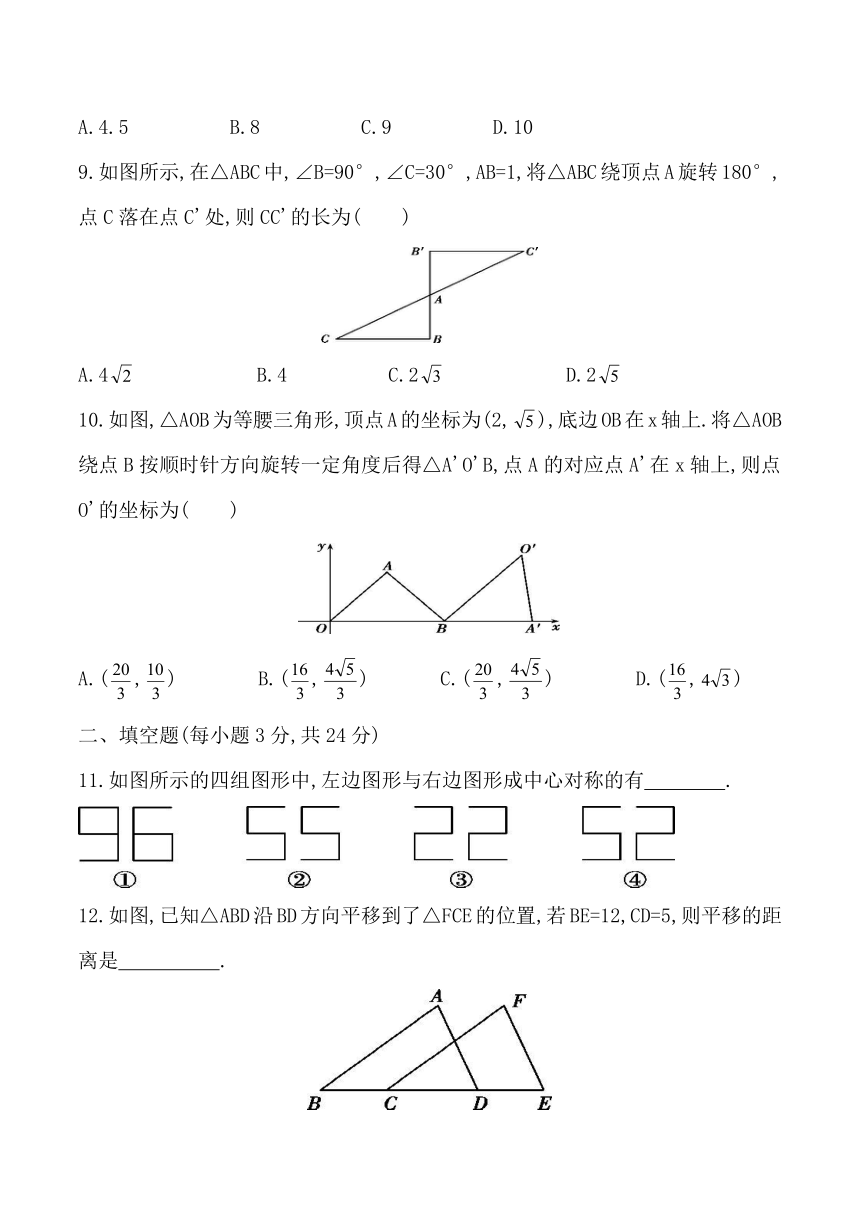
6.如图,将四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角不是旋转角的为( )
?
A.∠BOF ??B.∠AOD
C.∠COE ??D.∠AOF
7.如图,∠A=80°,O是AB上一点,直线OD与AB所夹的∠AOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )
A.8° ????B.10° ????C.12° ????D.18°
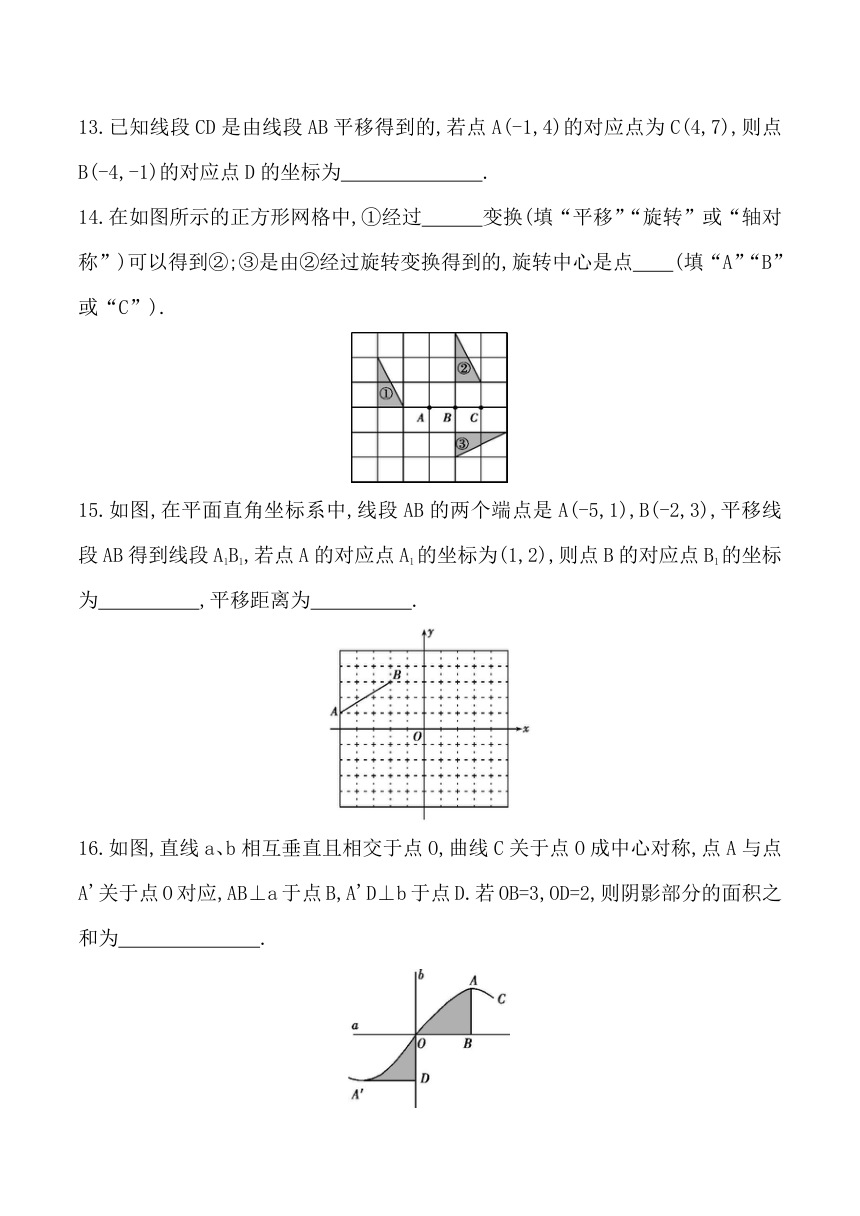
8.如图,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A'B'C'的位置,若平移的距离为2,则图中阴影部分的面积为( )
A.4.5 ????B.8 ????C.9 ????D.10
9.如图所示,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C'处,则CC'的长为( )
A.4? ????B.4 ????C.2? ????D.2?
10.如图,△AOB为等腰三角形,顶点A的坐标为(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
A.(,)? ??B.(,)?
C.(,)? ??D.(,)?
二、填空题(每小题3分,共24分)
11.如图所示的四组图形中,左边图形与右边图形成中心对称的有????.
12.如图,已知△ABD沿BD方向平移到了△FCE的位置,若BE=12,CD=5,则平移的距离是 ??.
13.已知线段CD是由线段AB平移得到的,若点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 ????.
14.在如图所示的正方形网格中,①经过 变换(填“平移”“旋转”或“轴对称”)可以得到②;③是由②经过旋转变换得到的,旋转中心是点 (填“A”“B”或“C”).
15.如图,在平面直角坐标系中,线段AB的两个端点是A(-5,1),B(-2,3),平移线段AB得到线段A1B1,若点A的对应点A1的坐标为(1,2),则点B的对应点B1的坐标为 ??,平移距离为 ??.
16.如图,直线a、b相互垂直且相交于点O,曲线C关于点O成中心对称,点A与点A'关于点O对应,AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 ????.
17.如图,在Rt△ABC中,∠ACB=90°,AC=5
cm,BC=12
cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F,则△ACF和△BDF的周长之和为 ??cm.
18.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②BE+DC=DE;③BE2+DC2=DE2,其中正确的是 ????.(填序号)
三、解答题(共46分)
19.(10分)如图,在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△AB1C1,使点C1落在直线BC上(点C1与点C不重合),求证:AB1∥CB.
20.(10分)如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°后得到△A1B1C,画出△A1B1C;
(2)平移△ABC至△A2B2C2的位置,若点A的对应点A2的坐标为(-5,-2),画出△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
21.(12分)如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图①中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系(不要求证明);
(2)当△DEF沿直线m向左平移到图②所示的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△ACE能否通过旋转重合.请证明你的猜想.
22.(14分)将两块大小相同的含30°角的直角三角板(∠BAC=∠B'A'C'=30°)按图①所示的方式放置,固定三角板A'B'C',然后将三角板ABC绕直角顶点C按顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A'C交于点E,AC与A'B'交于点F,AB与A'B'交于点O.
(1)求证:△BCE≌△B'CF;
(2)当旋转角等于30°时,AB与A'B'垂直吗?请说明理由.
答案
1.D
2.D
3.D
4.B
5.D
6.D
7.D
8.B
9.B
10.C
11.①②③
12.
13.(1,2)
14.平移;A
15.(4,4);
16.
6
17.
42
18.①③
19.
证明 ∵AB=BC,∴∠BAC=∠C.
由旋转的性质得,AC=AC1,∠BAC=∠B1AC1,
∴∠C=∠AC1C,
∴∠B1AC1=∠AC1C,∴AB1∥BC.
20.
(1)△A1B1C如图所示.
(2)△A2B2C2如图所示.
(3)旋转中心的坐标为(-1,0).
21.
(1)AB=AE,AB⊥AE.
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.
证明:∵AC⊥BC,DF⊥FE,
∴∠ACB=∠ACE=∠DFE=90°,
又∵AC=BC,DF=EF,∴∠DEF=∠D=45°.
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠GEC=45°,∴CG=CE.
在△BCG和△ACE中,?
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合.
22.
(1)证明:∵∠BCA=∠B'CA'=90°,
∴∠BCA-∠A'CA=∠B'CA'-∠A'CA,
即∠BCE=∠B'CF,
∵∠B=∠B',BC=B'C,
∴△BCE≌△B'CF.
(2)AB与A'B'垂直,理由如下:
旋转角等于30°,即∠ECF=30°,
又∵∠A=30°,
∴∠AEC=180°-∠A-∠ECF=120°.
由已知得∠B=∠B'=60°,
∵四边形OECB'的内角和为360°,
∴∠EOB'=360°-90°-120°-60°=90°,
∴AB与A'B'垂直.
图形的平移与旋转
一、选择题(每小题3分,共30分)
1.如图所示的图案中,为中心对称图形的是(??)
A.①② ??B.②③
C.②④ ??D.③④
2.下列四个图案中,不能由1号图形平移得到2号图形的是( )
3.观察图中的三个图形,照此规律,可知第四个图形是( )
4.如图,小聪坐在秋千上旋转了80°,其位置从P点运动到了P'点,则∠OPP'的度数为( )
A.40° ??B.50°
C.70° ??D.80°
5.如图,将正方形ABCD绕点D顺时针旋转90°后,点B的坐标变为(??)
A.(-2,2) ??B.(4,1)
C.(3,1)
??D.(4,0)
6.如图,将四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角不是旋转角的为( )
?
A.∠BOF ??B.∠AOD
C.∠COE ??D.∠AOF
7.如图,∠A=80°,O是AB上一点,直线OD与AB所夹的∠AOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )
A.8° ????B.10° ????C.12° ????D.18°
8.如图,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A'B'C'的位置,若平移的距离为2,则图中阴影部分的面积为( )
A.4.5 ????B.8 ????C.9 ????D.10
9.如图所示,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在点C'处,则CC'的长为( )
A.4? ????B.4 ????C.2? ????D.2?
10.如图,△AOB为等腰三角形,顶点A的坐标为(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
A.(,)? ??B.(,)?
C.(,)? ??D.(,)?
二、填空题(每小题3分,共24分)
11.如图所示的四组图形中,左边图形与右边图形成中心对称的有????.
12.如图,已知△ABD沿BD方向平移到了△FCE的位置,若BE=12,CD=5,则平移的距离是 ??.
13.已知线段CD是由线段AB平移得到的,若点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 ????.
14.在如图所示的正方形网格中,①经过 变换(填“平移”“旋转”或“轴对称”)可以得到②;③是由②经过旋转变换得到的,旋转中心是点 (填“A”“B”或“C”).
15.如图,在平面直角坐标系中,线段AB的两个端点是A(-5,1),B(-2,3),平移线段AB得到线段A1B1,若点A的对应点A1的坐标为(1,2),则点B的对应点B1的坐标为 ??,平移距离为 ??.
16.如图,直线a、b相互垂直且相交于点O,曲线C关于点O成中心对称,点A与点A'关于点O对应,AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 ????.
17.如图,在Rt△ABC中,∠ACB=90°,AC=5
cm,BC=12
cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F,则△ACF和△BDF的周长之和为 ??cm.
18.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②BE+DC=DE;③BE2+DC2=DE2,其中正确的是 ????.(填序号)
三、解答题(共46分)
19.(10分)如图,在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△AB1C1,使点C1落在直线BC上(点C1与点C不重合),求证:AB1∥CB.
20.(10分)如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°后得到△A1B1C,画出△A1B1C;
(2)平移△ABC至△A2B2C2的位置,若点A的对应点A2的坐标为(-5,-2),画出△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
21.(12分)如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图①中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系(不要求证明);
(2)当△DEF沿直线m向左平移到图②所示的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△ACE能否通过旋转重合.请证明你的猜想.
22.(14分)将两块大小相同的含30°角的直角三角板(∠BAC=∠B'A'C'=30°)按图①所示的方式放置,固定三角板A'B'C',然后将三角板ABC绕直角顶点C按顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A'C交于点E,AC与A'B'交于点F,AB与A'B'交于点O.
(1)求证:△BCE≌△B'CF;
(2)当旋转角等于30°时,AB与A'B'垂直吗?请说明理由.
答案
1.D
2.D
3.D
4.B
5.D
6.D
7.D
8.B
9.B
10.C
11.①②③
12.
13.(1,2)
14.平移;A
15.(4,4);
16.
6
17.
42
18.①③
19.
证明 ∵AB=BC,∴∠BAC=∠C.
由旋转的性质得,AC=AC1,∠BAC=∠B1AC1,
∴∠C=∠AC1C,
∴∠B1AC1=∠AC1C,∴AB1∥BC.
20.
(1)△A1B1C如图所示.
(2)△A2B2C2如图所示.
(3)旋转中心的坐标为(-1,0).
21.
(1)AB=AE,AB⊥AE.
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.
证明:∵AC⊥BC,DF⊥FE,
∴∠ACB=∠ACE=∠DFE=90°,
又∵AC=BC,DF=EF,∴∠DEF=∠D=45°.
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠GEC=45°,∴CG=CE.
在△BCG和△ACE中,?
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合.
22.
(1)证明:∵∠BCA=∠B'CA'=90°,
∴∠BCA-∠A'CA=∠B'CA'-∠A'CA,
即∠BCE=∠B'CF,
∵∠B=∠B',BC=B'C,
∴△BCE≌△B'CF.
(2)AB与A'B'垂直,理由如下:
旋转角等于30°,即∠ECF=30°,
又∵∠A=30°,
∴∠AEC=180°-∠A-∠ECF=120°.
由已知得∠B=∠B'=60°,
∵四边形OECB'的内角和为360°,
∴∠EOB'=360°-90°-120°-60°=90°,
∴AB与A'B'垂直.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
