2020-2021学年八年级数学人教版下册第十八章平行四边形单元练习试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第十八章平行四边形单元练习试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 536.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 00:00:00 | ||
图片预览



文档简介
人教版八年级数学下册第十八章《平行四边形》
单元练习题(含答案)
一、单选题
1.如图,在中,,,D是AB的中点,点E在AC上,点F在BC上,且,给出以下四个结论:(1);(2)是等腰直角三角形;(3)四边形CEDF面积;(4)的最小值为2.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
2.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A、B,把正方形沿箭头方向推,使点D落在y轴的正半轴上的点处,则点C的对应点的坐标为( )
A. B. C. D.
3.如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为( )
A.8 B.7
C.6 D.5
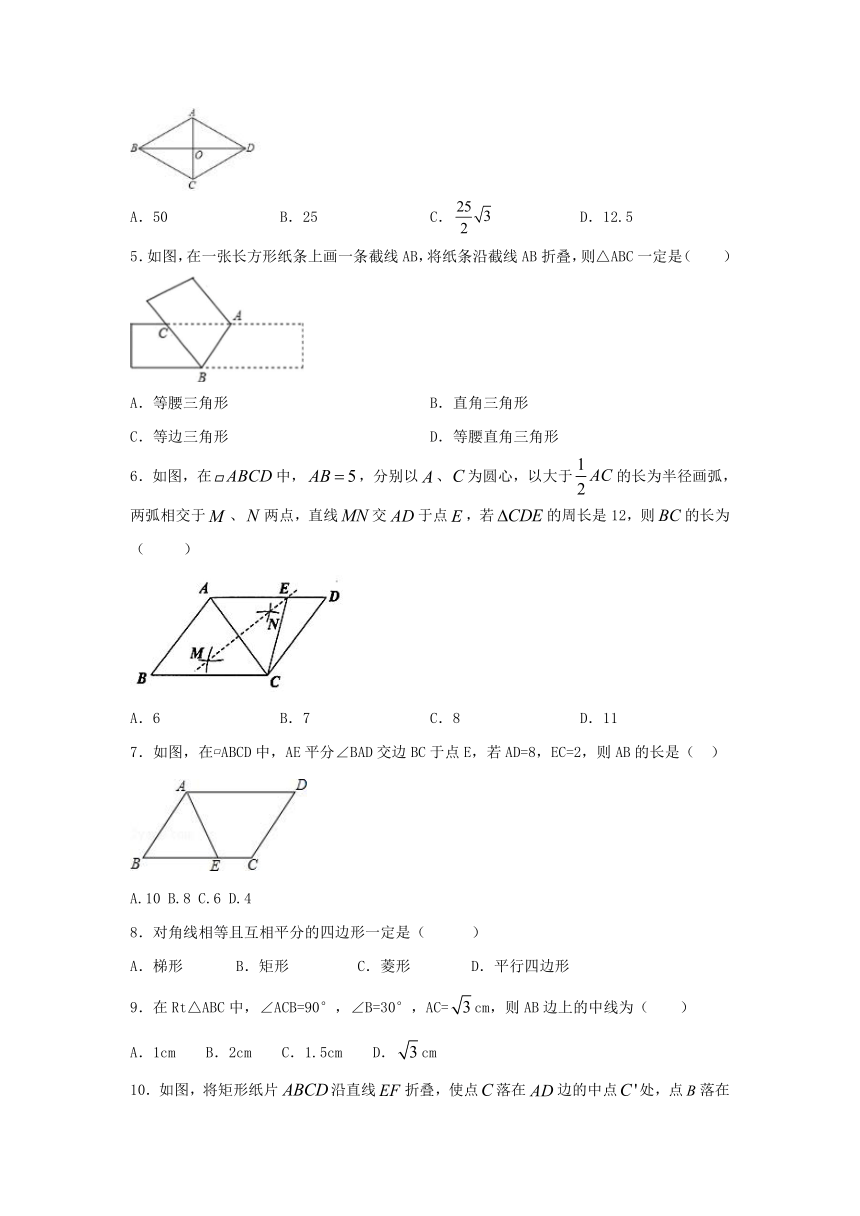
4.如图,菱形的对角线,,则该菱形的面积为( )
A.50 B.25 C. D.12.5
5.如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
6.如图,在中,,分别以、为圆心,以大于的长为半径画弧,两弧相交于、两点,直线交于点,若的周长是12,则的长为( )
A.6 B.7 C.8 D.11
7.如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )
A.10 B.8 C.6 D.4
8.对角线相等且互相平分的四边形一定是( )
A.梯形 B.矩形 C.菱形 D.平行四边形
9.在Rt△ABC中,∠ACB=90°,∠B=30°,AC=cm,则AB边上的中线为( )
A.1cm B.2cm C.1.5cm D.cm
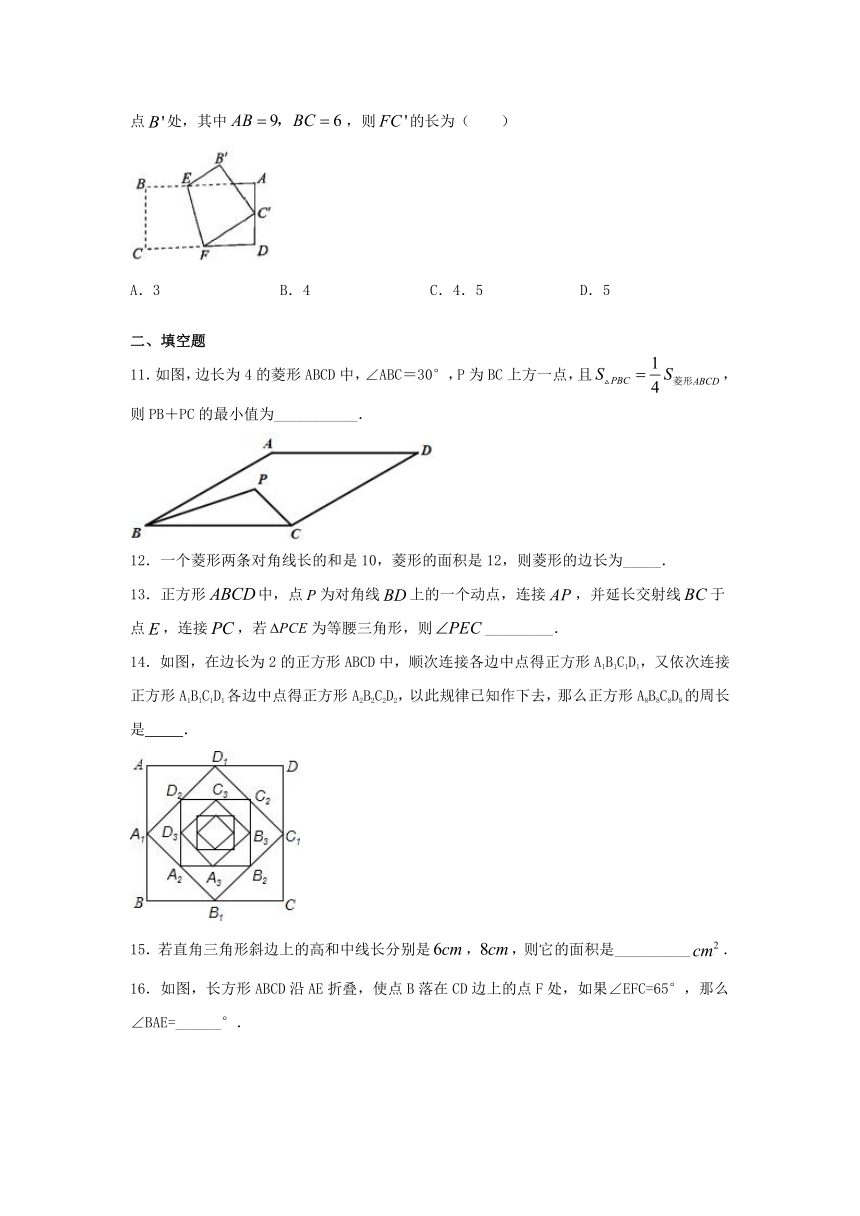
10.如图,将矩形纸片沿直线折叠,使点落在边的中点处,点落在点处,其中,则的长为( )
A.3 B.4 C.4.5 D.5
二、填空题
11.如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且,则PB+PC的最小值为___________.
12.一个菱形两条对角线长的和是10,菱形的面积是12,则菱形的边长为_____.
13.正方形中,点为对角线上的一个动点,连接,并延长交射线于点,连接,若为等腰三角形,则_________.
14.如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是 .
15.若直角三角形斜边上的高和中线长分别是,,则它的面积是__________.
16.如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=65°,那么∠BAE=______°.
17.如图所示,在□ABCD中,,,平分,,则_____.
18.如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则点B的坐标是__________.
三、解答题
19.在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1.
(1)请你在图1中画一个格点图形,且该图形是边长为的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出该格点正方形.
20.已知在四边形ABCD中,AD=BC,∠D=∠DCE,求证:四边形ABCD是平行四边形.
21.如图1,矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且,.
(1)在图2、图3中,点E、F分别在BC、CD边上,图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
(2)图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少;
(3)图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少.
22.已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.
23. 如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
24.如图,在长方形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处.
(1)求对角线的长;
(2)求的面积;
(3)求的长.
25.图1、图2分别是的网格,网格中的每个小正方形的边长均为1.请按要求画出下列图形,所画图形的各个项点均在所给小正方形的顶点上.
(1)在图1中画一个周长为的菱形.(非正方形)
(2)在图2中画出周长为18,面积为16的平行四边形.
26.下面是小林设计的“利用直角三角形作矩形”的尺规作图过程.
已知:在中,.
求作:矩形ABCD.
作法:如图②,
①分别以点A、C为圆心,大于长为半径作弧,两弧相交于点E、F;
②作直线EF,直线EF交AC于点O;
③作射线BO,在BO上截取OD,使得;
④连接AD,CD.
所以四边形ABCD就是所求的矩形.
根据小林设计的尺规作图过程.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:________,,
∴四边形ABCD为平行四边形(________________)(填推理依据).
又∵,
∴四边形ABCD为矩形(________________)(填推理依据).
27.阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙四边形”.
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABDC就称为“美妙四边形”.
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形,其中是“美妙四边形”的有 个;
(2)四边形ABCD是“美妙四边形”,AB=∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
参考答案
1.A2.A3.D4.B5.A6.B7.C8.B.9.D10.B
11.
12.
13.或
14.
15.48
16.12.5
17.1.5.
18.(5,0)
19.(1)如图1所示:四边形即为菱形;
(2)如图2,3所示:即为所求答案.
20.∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
21.(1)如下图;(2)定值是;(3)不是定值,分别是16、12
22.(1)20;
(2)如图所示(虚线可以不画),
23.证明:∵BE=DF,
∴BE﹣EF=DF﹣EF,即DE=BF.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.∴∠ADE=∠CBF.
∵在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS),
∴AE=CF.
24.(1);(2)30;(3)
25.
(1)如图1所示;
(2)如图2所示.
26.(1)补全图形,如图所示;
(2)证明:,,
∴四边形ABCD为平行四边形(对角线互相平分的四边形为平行四边形).
又∵,
∴四边形ABCD为矩形(有一个内角为90°的平行四边形为矩形).
故答案为:OC;对角线互相平分的四边形为平行四边形;有一个内角为90°的平行四边形为矩形.
27.(1)2 ;(2)或.
单元练习题(含答案)
一、单选题
1.如图,在中,,,D是AB的中点,点E在AC上,点F在BC上,且,给出以下四个结论:(1);(2)是等腰直角三角形;(3)四边形CEDF面积;(4)的最小值为2.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
2.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A、B,把正方形沿箭头方向推,使点D落在y轴的正半轴上的点处,则点C的对应点的坐标为( )
A. B. C. D.
3.如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为( )
A.8 B.7
C.6 D.5
4.如图,菱形的对角线,,则该菱形的面积为( )
A.50 B.25 C. D.12.5
5.如图,在一张长方形纸条上画一条截线AB,将纸条沿截线AB折叠,则△ABC一定是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
6.如图,在中,,分别以、为圆心,以大于的长为半径画弧,两弧相交于、两点,直线交于点,若的周长是12,则的长为( )
A.6 B.7 C.8 D.11
7.如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )
A.10 B.8 C.6 D.4
8.对角线相等且互相平分的四边形一定是( )
A.梯形 B.矩形 C.菱形 D.平行四边形
9.在Rt△ABC中,∠ACB=90°,∠B=30°,AC=cm,则AB边上的中线为( )
A.1cm B.2cm C.1.5cm D.cm
10.如图,将矩形纸片沿直线折叠,使点落在边的中点处,点落在点处,其中,则的长为( )
A.3 B.4 C.4.5 D.5
二、填空题
11.如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且,则PB+PC的最小值为___________.
12.一个菱形两条对角线长的和是10,菱形的面积是12,则菱形的边长为_____.
13.正方形中,点为对角线上的一个动点,连接,并延长交射线于点,连接,若为等腰三角形,则_________.
14.如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是 .
15.若直角三角形斜边上的高和中线长分别是,,则它的面积是__________.
16.如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=65°,那么∠BAE=______°.
17.如图所示,在□ABCD中,,,平分,,则_____.
18.如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则点B的坐标是__________.
三、解答题
19.在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1.
(1)请你在图1中画一个格点图形,且该图形是边长为的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出该格点正方形.
20.已知在四边形ABCD中,AD=BC,∠D=∠DCE,求证:四边形ABCD是平行四边形.
21.如图1,矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且,.
(1)在图2、图3中,点E、F分别在BC、CD边上,图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
(2)图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少;
(3)图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少.
22.已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.
23. 如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
24.如图,在长方形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处.
(1)求对角线的长;
(2)求的面积;
(3)求的长.
25.图1、图2分别是的网格,网格中的每个小正方形的边长均为1.请按要求画出下列图形,所画图形的各个项点均在所给小正方形的顶点上.
(1)在图1中画一个周长为的菱形.(非正方形)
(2)在图2中画出周长为18,面积为16的平行四边形.
26.下面是小林设计的“利用直角三角形作矩形”的尺规作图过程.
已知:在中,.
求作:矩形ABCD.
作法:如图②,
①分别以点A、C为圆心,大于长为半径作弧,两弧相交于点E、F;
②作直线EF,直线EF交AC于点O;
③作射线BO,在BO上截取OD,使得;
④连接AD,CD.
所以四边形ABCD就是所求的矩形.
根据小林设计的尺规作图过程.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:________,,
∴四边形ABCD为平行四边形(________________)(填推理依据).
又∵,
∴四边形ABCD为矩形(________________)(填推理依据).
27.阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙四边形”.
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABDC就称为“美妙四边形”.
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形,其中是“美妙四边形”的有 个;
(2)四边形ABCD是“美妙四边形”,AB=∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
参考答案
1.A2.A3.D4.B5.A6.B7.C8.B.9.D10.B
11.
12.
13.或
14.
15.48
16.12.5
17.1.5.
18.(5,0)
19.(1)如图1所示:四边形即为菱形;
(2)如图2,3所示:即为所求答案.
20.∵∠D=∠DCE,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.
21.(1)如下图;(2)定值是;(3)不是定值,分别是16、12
22.(1)20;
(2)如图所示(虚线可以不画),
23.证明:∵BE=DF,
∴BE﹣EF=DF﹣EF,即DE=BF.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.∴∠ADE=∠CBF.
∵在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS),
∴AE=CF.
24.(1);(2)30;(3)
25.
(1)如图1所示;
(2)如图2所示.
26.(1)补全图形,如图所示;
(2)证明:,,
∴四边形ABCD为平行四边形(对角线互相平分的四边形为平行四边形).
又∵,
∴四边形ABCD为矩形(有一个内角为90°的平行四边形为矩形).
故答案为:OC;对角线互相平分的四边形为平行四边形;有一个内角为90°的平行四边形为矩形.
27.(1)2 ;(2)或.
