2020-2021高三下学期第一次月考数学理科试题Word含答案
文档属性
| 名称 | 2020-2021高三下学期第一次月考数学理科试题Word含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 22:45:13 | ||
图片预览


文档简介
×××学校
2020-2021学年度下学期高三第一次月考试题
数学(理)
满分100分,考试时间为120分钟。
一、本题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.设集合,,则下列关系中正确的( )
A. B.
C. D.
2.复数的虚部为 ( )
A. B. C.― D.―
3.根据下列三视图(如下图所示),则它的体积是 ( )
A. B. C. D.
4.函数的图象如图所示,为了得到的图像,可以将的图像 ( )
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
5.已知x,y满足不等式组的最小值为 ( )
A. B.2 C.3 D.
6.右图是一个算法的程序框图,该算法所输出的结果是 ( )
A. B. C. D.
7.设圆锥曲线C的两个焦点分别为F1,F2,若曲线r上存在点P满足=4:3:2,则曲线C的离心率等于 ( )
A. B.或2
C.2 D.
8.已知抛物线的一条过焦点F的弦PQ,点R在直线
PQ上,且满足,R在抛物线准线上的射影为,设是中的两个锐角,则下列四个式子中不一定正确的是( )
A. B.
C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分
(9-----13为必做题,14、15选一个作答,如果都选,按14题计分)
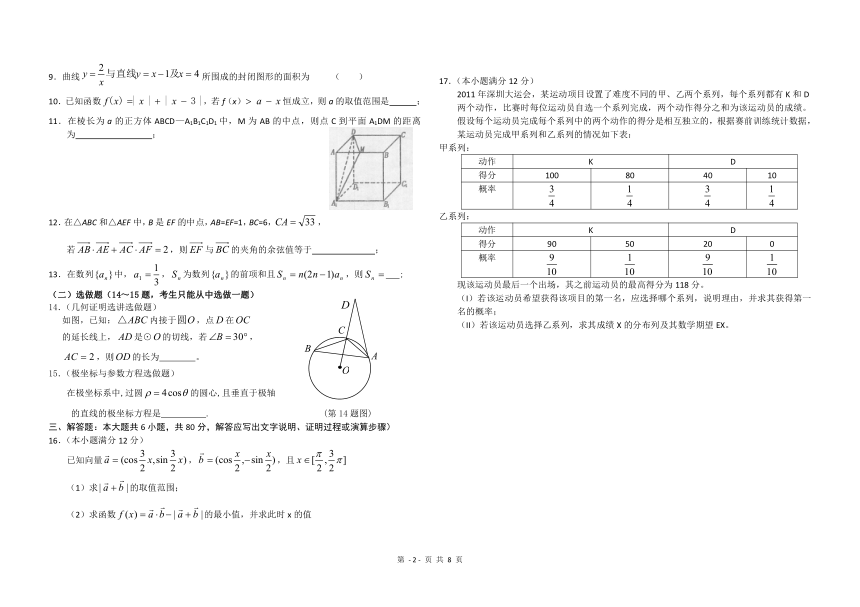
9.曲线所围成的封闭图形的面积为 ( )
10.已知函数,若f(x)恒成立,则a的取值范围是 ;
11.在棱长为a的正方体ABCD—A1B1C1D1中,M为AB的中点,则点C到平面A1DM的距离为 ;
12.在△ABC和△AEF中,B是EF的中点,AB=EF=1,BC=6,,若,则与的夹角的余弦值等于 ;
13.在数列中,,为数列的前项和且,则 ;
(二)选做题(14~15题,考生只能从中选做一题)
14.(几何证明选讲选做题)
如图,已知:内接于,点在
的延长线上,是⊙的切线,若,
,则的长为 。
15.(极坐标与参数方程选做题)
在极坐标系中,过圆的圆心,且垂直于极轴
的直线的极坐标方程是 . (第14题图)
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)
已知向量,,且
(1)求的取值范围;
(2)求函数的最小值,并求此时x的值
17.(本小题满分12分)
2011年深圳大运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
动作 K D
得分 100 80 40 10
概率
乙系列:
动作 K D
得分 90 50 20 0
概率
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
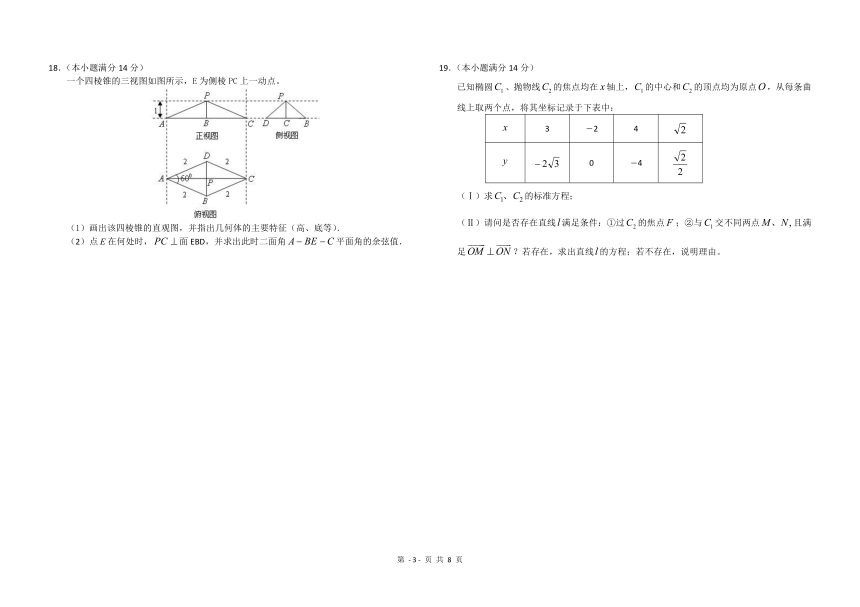
18.(本小题满分14分)
一个四棱锥的三视图如图所示,E为侧棱PC上一动点。
(1)画出该四棱锥的直观图,并指出几何体的主要特征(高、底等).
(2)点在何处时,面EBD,并求出此时二面角平面角的余弦值.
19.(本小题满分14分)
已知椭圆、抛物线的焦点均在轴上,的中心和的顶点均为原点,从每条曲线上取两个点,将其坐标记录于下表中:
3 2 4
0 4
(Ⅰ)求的标准方程;
(Ⅱ)请问是否存在直线满足条件:①过的焦点;②与交不同两点且满足?若存在,求出直线的方程;若不存在,说明理由。
20.(本小题满分14分) 已知函数,且函数是上的增函数。
(1)求的取值范围;
(2)若对任意的,都有(e是自然对数的底),求满足条件的最大整数的值。
21、已知等比数列的首项,公比,数列前n项和记为,前n
项积记为.
(Ⅰ)求数列的最大项和最小项;
(Ⅱ)判断与的大小, 并求为何值时,取得最大值;
(Ⅲ)证明中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为,证明:数列为等比数列。(参考数据)
×××学校
2020-2021学年度下学期高三第一次月考试题
数学(理)参考答案
一.选择题 B B. D;.B.D. C.A ;D;
题号 1 2 3 4 5 6 7 8
答案 B B D B D C A D
二.填空题
9、 10.(-∞,3); 11.; 12.;
13. 选作 14. 4 15.
三.解答题
16.解析:(1)∵ ∴
∴ 0≤≤2 4分
(2)∵ ∴ ;…………6分
∵
………………10分
∴ 当,即或时,取最小值-。
……………………12分
17.解析:(I)若该运动员希望获得该项目的第一名,应选择甲系列.……1分
理由如下:选择甲系列最高得分为100+40=140>118,可能获得第一名;而选择乙系列最高得分为90+20=110<118,不可能获得第一名. ……2分
记“该运动员完成K动作得100分”为事件A,“该运动员完成D动作得40分”为事件B,则P (A)=,P (B)=. …………4分
记“该运动员获得第一名”为事件C,依题意得
P (C)=P (AB)+==.
该运动员获得第一名的概率为.…………6分
(II)若该运动员选择乙系列,X的可能取值是50,70,90,110, …………7分
则P (X=50)==,
P (X=70)==,P (X=90)==,
P (X=110)==. …………9分
X的分布列为:
X 50 70 90 110
P
∴=50×+70×+90×+110×=104. ……12分
18.解析:
(1)直观图如下:………………3分
该四棱锥底面为菱形,边长为2,其中角A为60度,顶点A在底面内的射影为底面菱形的中心,四棱锥高为1。………………5分
(2)如图所示建立空间直角坐标系:
显然A、B、P.
令,得:、.
显然,
当.
所以当时,面BDE。………………9分
分别令和为平面PBC和平面ABE的法向量,
由,得
由,得
可得:,
显然二面角平面角为钝角,得其余弦值为。…………14分
19.解析:(Ⅰ)设抛物线,则有,据此验证个点知(3,)、(4,4)在抛物线上,易求 ………………3分
设:,把点(2,0)(,)代入得:
解得
∴方程为 ………………………………………………………………6分
(Ⅱ)法一:
假设存在这样的直线过抛物线焦点,设直线的方程为两交点坐标为,
由消去,得…………………………9分
∴ ①
② ………………………10分
由,即,得
将①②代入(*)式,得, 解得 …………………13分
所以假设成立,即存在直线满足条件,且的方程为:或…………………………………………………………………………………14分
法二:容易验证直线的斜率不存在时,不满足题意;……………………………7分
当直线斜率存在时,假设存在直线过抛物线焦点,设其方程为,与的交点坐标为
由消掉,得 , …………9分
于是 , ①
即 ② ………………………………11分
由,即,得
将①、②代入(*)式,得 ,解得;……13分
所以存在直线满足条件,且的方程为:或.………14分
20.解析:(1)设,所以,得到.所以的取值范围为………2分
(2)令,因为是上的增函数,且,所以是上的增函数。…………………………4分
由条件得到(两边取自然对数),猜测最大整数,现在证明对任意恒成立。…………6分
等价于,………………8分
设,
当时,,当时,,
所以对任意的都有,即对任意恒成立,
所以整数的最大值为2.……………………………………………………14分
21解:(Ⅰ)
当n是奇数时,, 单调递减,,
当n是偶数时,, 单调递增,;
综上,当n=1时,; 当n=2时,. ………………………4分
(Ⅱ),
,
,
则当时,;当时,,……7分
又,
的最大值是中的较大者.
,,
因此当n=12时,最大. ………………………9分
(Ⅲ)随n增大而减小,数列的奇数项均正数且递减,偶数项均负数且递增.
①当n是奇数时,调整为.则
,,
成等差数列; ………………………11分
②当n是偶数时,调整为;则
,,
成等差数列;
综上可知,数列中的任意相邻三项按从小到大排列,总可以使其成等差数列.……12分
①n是奇数时,公差;
②n是偶数时,公差.
无论n是奇数还是偶数,都有,则,
因此,数列是首项为,公比为的等比数列. ………………………14分
第 - 6 - 页 共 8 页
2020-2021学年度下学期高三第一次月考试题
数学(理)
满分100分,考试时间为120分钟。
一、本题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.设集合,,则下列关系中正确的( )
A. B.
C. D.
2.复数的虚部为 ( )
A. B. C.― D.―
3.根据下列三视图(如下图所示),则它的体积是 ( )
A. B. C. D.
4.函数的图象如图所示,为了得到的图像,可以将的图像 ( )
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
5.已知x,y满足不等式组的最小值为 ( )
A. B.2 C.3 D.
6.右图是一个算法的程序框图,该算法所输出的结果是 ( )
A. B. C. D.
7.设圆锥曲线C的两个焦点分别为F1,F2,若曲线r上存在点P满足=4:3:2,则曲线C的离心率等于 ( )
A. B.或2
C.2 D.
8.已知抛物线的一条过焦点F的弦PQ,点R在直线
PQ上,且满足,R在抛物线准线上的射影为,设是中的两个锐角,则下列四个式子中不一定正确的是( )
A. B.
C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分
(9-----13为必做题,14、15选一个作答,如果都选,按14题计分)
9.曲线所围成的封闭图形的面积为 ( )
10.已知函数,若f(x)恒成立,则a的取值范围是 ;
11.在棱长为a的正方体ABCD—A1B1C1D1中,M为AB的中点,则点C到平面A1DM的距离为 ;
12.在△ABC和△AEF中,B是EF的中点,AB=EF=1,BC=6,,若,则与的夹角的余弦值等于 ;
13.在数列中,,为数列的前项和且,则 ;
(二)选做题(14~15题,考生只能从中选做一题)
14.(几何证明选讲选做题)
如图,已知:内接于,点在
的延长线上,是⊙的切线,若,
,则的长为 。
15.(极坐标与参数方程选做题)
在极坐标系中,过圆的圆心,且垂直于极轴
的直线的极坐标方程是 . (第14题图)
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)
已知向量,,且
(1)求的取值范围;
(2)求函数的最小值,并求此时x的值
17.(本小题满分12分)
2011年深圳大运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
动作 K D
得分 100 80 40 10
概率
乙系列:
动作 K D
得分 90 50 20 0
概率
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
18.(本小题满分14分)
一个四棱锥的三视图如图所示,E为侧棱PC上一动点。
(1)画出该四棱锥的直观图,并指出几何体的主要特征(高、底等).
(2)点在何处时,面EBD,并求出此时二面角平面角的余弦值.
19.(本小题满分14分)
已知椭圆、抛物线的焦点均在轴上,的中心和的顶点均为原点,从每条曲线上取两个点,将其坐标记录于下表中:
3 2 4
0 4
(Ⅰ)求的标准方程;
(Ⅱ)请问是否存在直线满足条件:①过的焦点;②与交不同两点且满足?若存在,求出直线的方程;若不存在,说明理由。
20.(本小题满分14分) 已知函数,且函数是上的增函数。
(1)求的取值范围;
(2)若对任意的,都有(e是自然对数的底),求满足条件的最大整数的值。
21、已知等比数列的首项,公比,数列前n项和记为,前n
项积记为.
(Ⅰ)求数列的最大项和最小项;
(Ⅱ)判断与的大小, 并求为何值时,取得最大值;
(Ⅲ)证明中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为,证明:数列为等比数列。(参考数据)
×××学校
2020-2021学年度下学期高三第一次月考试题
数学(理)参考答案
一.选择题 B B. D;.B.D. C.A ;D;
题号 1 2 3 4 5 6 7 8
答案 B B D B D C A D
二.填空题
9、 10.(-∞,3); 11.; 12.;
13. 选作 14. 4 15.
三.解答题
16.解析:(1)∵ ∴
∴ 0≤≤2 4分
(2)∵ ∴ ;…………6分
∵
………………10分
∴ 当,即或时,取最小值-。
……………………12分
17.解析:(I)若该运动员希望获得该项目的第一名,应选择甲系列.……1分
理由如下:选择甲系列最高得分为100+40=140>118,可能获得第一名;而选择乙系列最高得分为90+20=110<118,不可能获得第一名. ……2分
记“该运动员完成K动作得100分”为事件A,“该运动员完成D动作得40分”为事件B,则P (A)=,P (B)=. …………4分
记“该运动员获得第一名”为事件C,依题意得
P (C)=P (AB)+==.
该运动员获得第一名的概率为.…………6分
(II)若该运动员选择乙系列,X的可能取值是50,70,90,110, …………7分
则P (X=50)==,
P (X=70)==,P (X=90)==,
P (X=110)==. …………9分
X的分布列为:
X 50 70 90 110
P
∴=50×+70×+90×+110×=104. ……12分
18.解析:
(1)直观图如下:………………3分
该四棱锥底面为菱形,边长为2,其中角A为60度,顶点A在底面内的射影为底面菱形的中心,四棱锥高为1。………………5分
(2)如图所示建立空间直角坐标系:
显然A、B、P.
令,得:、.
显然,
当.
所以当时,面BDE。………………9分
分别令和为平面PBC和平面ABE的法向量,
由,得
由,得
可得:,
显然二面角平面角为钝角,得其余弦值为。…………14分
19.解析:(Ⅰ)设抛物线,则有,据此验证个点知(3,)、(4,4)在抛物线上,易求 ………………3分
设:,把点(2,0)(,)代入得:
解得
∴方程为 ………………………………………………………………6分
(Ⅱ)法一:
假设存在这样的直线过抛物线焦点,设直线的方程为两交点坐标为,
由消去,得…………………………9分
∴ ①
② ………………………10分
由,即,得
将①②代入(*)式,得, 解得 …………………13分
所以假设成立,即存在直线满足条件,且的方程为:或…………………………………………………………………………………14分
法二:容易验证直线的斜率不存在时,不满足题意;……………………………7分
当直线斜率存在时,假设存在直线过抛物线焦点,设其方程为,与的交点坐标为
由消掉,得 , …………9分
于是 , ①
即 ② ………………………………11分
由,即,得
将①、②代入(*)式,得 ,解得;……13分
所以存在直线满足条件,且的方程为:或.………14分
20.解析:(1)设,所以,得到.所以的取值范围为………2分
(2)令,因为是上的增函数,且,所以是上的增函数。…………………………4分
由条件得到(两边取自然对数),猜测最大整数,现在证明对任意恒成立。…………6分
等价于,………………8分
设,
当时,,当时,,
所以对任意的都有,即对任意恒成立,
所以整数的最大值为2.……………………………………………………14分
21解:(Ⅰ)
当n是奇数时,, 单调递减,,
当n是偶数时,, 单调递增,;
综上,当n=1时,; 当n=2时,. ………………………4分
(Ⅱ),
,
,
则当时,;当时,,……7分
又,
的最大值是中的较大者.
,,
因此当n=12时,最大. ………………………9分
(Ⅲ)随n增大而减小,数列的奇数项均正数且递减,偶数项均负数且递增.
①当n是奇数时,调整为.则
,,
成等差数列; ………………………11分
②当n是偶数时,调整为;则
,,
成等差数列;
综上可知,数列中的任意相邻三项按从小到大排列,总可以使其成等差数列.……12分
①n是奇数时,公差;
②n是偶数时,公差.
无论n是奇数还是偶数,都有,则,
因此,数列是首项为,公比为的等比数列. ………………………14分
第 - 6 - 页 共 8 页
同课章节目录
