2020-2021学年八年级下册第19章一次函数章末复习课件(23张)
文档属性
| 名称 | 2020-2021学年八年级下册第19章一次函数章末复习课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 400.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 21:59:06 | ||
图片预览







文档简介
(共23张PPT)
八年级下册
一次函数
章末复习
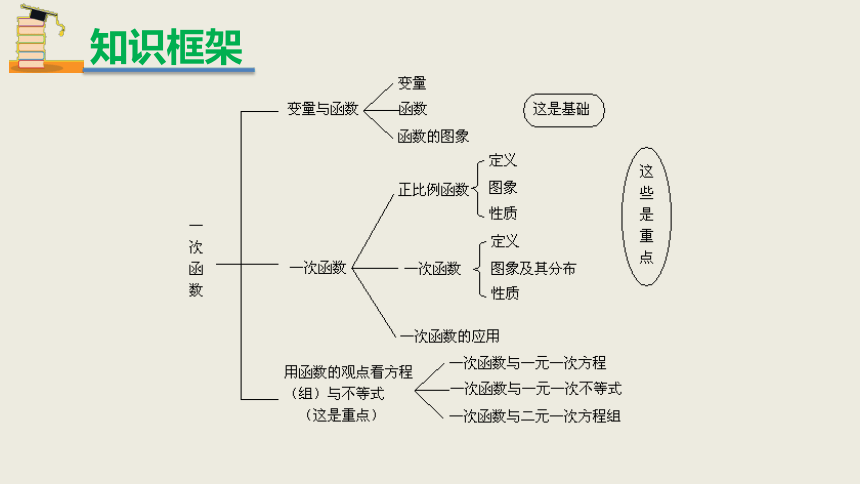
知识框架
知识回顾
1.
变量与函数
变量:在一个变化过程中可以取不同数值的量.
常量:在一个变化过程中只能取同一数值的量.
函数:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,
y是x的函数.
函数的三种表示方法:列表法、图象法、解析法.
确定函数自变量取值范围的方法:
(1)关系式为整式时,函数定义域为全体实数;
(2)关系式含有分式时,分式的分母不等于零;
(3)关系式含有二次根式时,被开方数大于等于零;
(4)关系式中含有指数为零的式子时,底数不等于零;
(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义.
考点对接
确定自变量的取值范围
1.下列函数中,自变量的取值范围选取错误的是(
)
A.y=2x?,x取全体实数
B.y=
中,x取x≠-1的实数
C.y=
中,x取x≥2的实数
D.y=
中,x取x≥-3的实数
变量之间的关系是否函数关系
2.下列变量之间的关系不是函数关系的是(
)
A.长方形的宽一定,其长与面积
B.正方形的周长和面积
C.等腰三角形的底边长和面积
D.某人的年龄与身高
3.已知函数
,当
时,y的取值范围是
(
)
A.
B.
C.
D.
D
C
C
知识回顾
2.
一次函数
⑵一次函数
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
图象:过(0,b)和(-
,0)是一条直线.
当k>0,图像经过一、三象限;y随x的增大而增大;k<0,图像经过二、四象限,y随x增大而减小.
当b>0时,直线与y轴交于正半轴上,图像经过一、二象限;
当b<0时,直线与y轴交于负半轴上;图像经过三、四象限.
当b=0时,直线经过原点,是正比例函数.
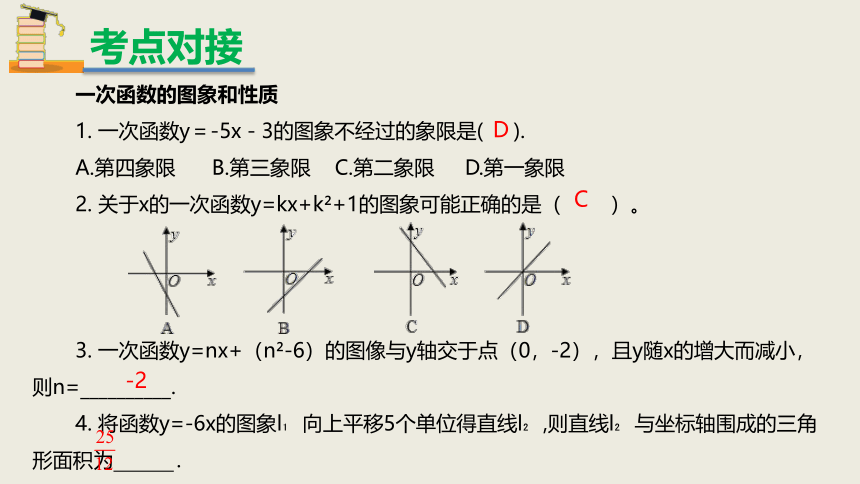
一次函数的图象和性质
1.
一次函数y=-5x-3的图象不经过的象限是(
).
A.第四象限
B.第三象限
C.第二象限
D.第一象限
2.
关于x的一次函数y=kx+k?+1的图象可能正确的是(
)。
3.
一次函数y=nx+(n?-6)的图像与y轴交于点(0,-2),且y随x的增大而减小,则n=__________.
4.
将函数y=-6x的图象l?向上平移5个单位得直线l?,则直线l?与坐标轴围成的三角形面积为
.
考点对接
D
C
-2
知识回顾
3.一次函数的确定
一般步骤(一设二代三解四还原):
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
考点对接
1.如图,过A点的一次函数的图象与正比例函数y=2x的图
象相交于点B,则这个一次函数的解析式是(
)
A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
2.
甲、乙两工程队同时修筑水水渠且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图像的一部分.请根据图中信息,解答下列问题:
(1)直接写出甲队在0≤x≤5的时间段内,
y关于x的函数解析式为
.
(2)直接写出乙队在2≤x≤5的时间段内,
y关于x的函数解析式为
.
D
y=10x
y=20x-30
3.
已知点P(x,y)是第一象限内一次函数y=-x+6图象上的一点(点P不在坐标轴上),点A的坐标是(4,0),
?PAO的面积为S.
(1)求S与x的函数关系;
(2)求自变量x的取值范围.
解:(1)
∵点P(x,y)是第一象限内一次函数y=-x+6图象上的一点
(点P不在坐标轴上),点A的坐标是(4,0),
∴?PAO的面积为
S=
×4×(-x+6)=-2x+12,
(2)
∵点P在第一象限内,
∴0<x<6.
知识回顾
4.一次函数的应用
一次函数与一元一次方程、一元一次不等式、二元一次方程(组)的关系
一次函数的实际应用.
考点对接
D
1.
小亮从家步行到公交车站台,等公交车去学校。图中的折线表示小亮的行程S(km)与所花时间t(min)之间的函数关系。下列说法错误的是(
)。
A.
他离家共用了30min
B.
他等公交车时间为6min
C.
他步行的速度是100m/min
D.
公交车的速度是350/min
2.
“五一节”期间,申老师一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(时)之间的函数图象。
(1)求他们出发半小时时,离家多少千米。
(2)求出AB段图象的函数表达式。
(3)他们出发2小时时,离目的地还有多少千米。
(1)设OA段图象的函数表达式为y=k?x,将点(1.5,90)代入得
k?==
5=60,
∴OA段图象函数表达式为y=60x(0≤x≤1.5)
出发半小时,离家的距离y=60x×0.5=30(千米)。
(2)设AB段图象的函数表达式为y=k?x+b,将点A(1.5,90)与B(2.5,170)代入得
1.5k?+b=90
①,2.5k?+b=170,
解得:k?=80,b=-30,
则AB段图象的函数表达式为y=80x-30(1.5≤x≤2.5).
(3)当x=2时,代入AB段函数表达式得y=80x-30=80×2-30=130(千米),
离目的地还有170-130=40(千米)。
3.
手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式。方式A:以每分钟0.1元的价格按上网时间计费;方式B:除收月基费20元外,再以每分钟0.06元的价格按上网时间计费。假设某客户月手机上网的时间为x分钟,上网费用为y元。
(1)分别写出该客户按A、B两种方式的上网费y(元)与每月上网时间x(分钟)的函数关系式,并在图中的坐标系中画出这两个函数的图象。
(2)如何选择计费方式能使该客户上网费用更合算?
(1)由题意得:方式A:yA=0.1x,
方式B:yB=0.06x+20,
函数图象如图所示。
(2)如何选择计费方式能使该客户上网费用更合算?
(2)当yA=yB,即0.1x=0.06x+20时,解得:x=500;
当yA<yB,即0.1x<0.06x+20时,解得:x<500;
yA<yB,即0.1x<0.06x+20时,解得:x>500.
所以当月手机上网时间小于500分钟时,选择方式A上网更合算;当月手机上网时间等于500分钟时,选择方式A和方式B上网一样合算;当月手机上网时间大于500分钟时,选择方式B上网更合算。
随堂检测
1.若b>0,则一次函数y=-x+b的图象大致是(
)
2.下列函数中,对于任意实数x1,x2,当x1>x2时,满足y1<y2的是(
)
A.y=-3x+2
B.y=2x+1
C.y=2x2+1
D.y=-1/x
C
A
3.如图,直线l是一次函数y=kx+b的图象,如果点A(3,m)在直线l上,则m的值为(
)
A.-5
B.3/2
C.5/2
D.7
4.对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,-1}=-1,若关于x的函数y=min{2x-1,-x+3},则该函数的最大值为(
)
A.2/3
B.1
C.4/3
D.5/3
C
D
5.将直线y=
x向上平移2个单位长度,平移后直线的解析式为
.
6.如图,直线y=kx+b交x轴于点A,交y轴于点B,
则不等式x(kx+b)<0的解集为
.
7.设点(-1,m)和点(1/2,n)是直线y=(k2-1)x+b
(0<k<1)上的两个点,则m,n的大小关系为
.
8.
如图,一次函数的图象与x轴、y轴分别相交于点A,B,将△AOB沿直线AB翻折得△ACB
.若C(
),则该
一次函数的解析式为
.
y=x+2
-3<x<0
m>n
y=-
x+
9.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
解
:(1)设一次函数的解析式为y=kx+b,
则-3=-2k+b
①,3=k+b
②,
由①、②得k=2,b=1,
∴函数的解析式为y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0时,y=1,当y=0时,x=-12,
此函数与x轴、y轴围成的三角形的面积为?×1×|-?|=?.
10.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地。设先发车辆行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系。根据图象解决以下问题。
(1)慢车的速度为
km/h,快车的速度为
km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300
km.
解:(2)慢车走完全程需要480÷80=6h,快车走完全程需要480÷120=4h,而慢车仅比快车早出发0.5h,故快车先到达乙地。图中点D的实际意义为快车到达了乙地,此时慢车已经行驶了4+0,5=4.5h,此时两车的距离为(80+120)×(4.5-2.7)=360km。
两车相距360km,点D的坐标为(4.5,360)。
80
120
10.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地。设先发车辆行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系。根据图象解决以下问题。
(1)慢车的速度为
km/h,快车的速度为
km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300
km.
解:(3)由题意可知两车有两次距离为300。
相遇前:(80+120)(x-0.5)=440-300,解得x=1.2;
相遇后:(80+120)(x-2.7)=300,解得x=4.2。
综上所述,当x=1.2或x=4.2时,两车之间的距离为300km。
80
120
1.三个概念:函数、正比例函数、一次函数;
2.一个性质:一次函数的性质;
3.一个应用:一次函数的应用;
课堂小结
再见
八年级下册
一次函数
章末复习
知识框架
知识回顾
1.
变量与函数
变量:在一个变化过程中可以取不同数值的量.
常量:在一个变化过程中只能取同一数值的量.
函数:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,
y是x的函数.
函数的三种表示方法:列表法、图象法、解析法.
确定函数自变量取值范围的方法:
(1)关系式为整式时,函数定义域为全体实数;
(2)关系式含有分式时,分式的分母不等于零;
(3)关系式含有二次根式时,被开方数大于等于零;
(4)关系式中含有指数为零的式子时,底数不等于零;
(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义.
考点对接
确定自变量的取值范围
1.下列函数中,自变量的取值范围选取错误的是(
)
A.y=2x?,x取全体实数
B.y=
中,x取x≠-1的实数
C.y=
中,x取x≥2的实数
D.y=
中,x取x≥-3的实数
变量之间的关系是否函数关系
2.下列变量之间的关系不是函数关系的是(
)
A.长方形的宽一定,其长与面积
B.正方形的周长和面积
C.等腰三角形的底边长和面积
D.某人的年龄与身高
3.已知函数
,当
时,y的取值范围是
(
)
A.
B.
C.
D.
D
C
C
知识回顾
2.
一次函数
⑵一次函数
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
图象:过(0,b)和(-
,0)是一条直线.
当k>0,图像经过一、三象限;y随x的增大而增大;k<0,图像经过二、四象限,y随x增大而减小.
当b>0时,直线与y轴交于正半轴上,图像经过一、二象限;
当b<0时,直线与y轴交于负半轴上;图像经过三、四象限.
当b=0时,直线经过原点,是正比例函数.
一次函数的图象和性质
1.
一次函数y=-5x-3的图象不经过的象限是(
).
A.第四象限
B.第三象限
C.第二象限
D.第一象限
2.
关于x的一次函数y=kx+k?+1的图象可能正确的是(
)。
3.
一次函数y=nx+(n?-6)的图像与y轴交于点(0,-2),且y随x的增大而减小,则n=__________.
4.
将函数y=-6x的图象l?向上平移5个单位得直线l?,则直线l?与坐标轴围成的三角形面积为
.
考点对接
D
C
-2
知识回顾
3.一次函数的确定
一般步骤(一设二代三解四还原):
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
考点对接
1.如图,过A点的一次函数的图象与正比例函数y=2x的图
象相交于点B,则这个一次函数的解析式是(
)
A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
2.
甲、乙两工程队同时修筑水水渠且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图像的一部分.请根据图中信息,解答下列问题:
(1)直接写出甲队在0≤x≤5的时间段内,
y关于x的函数解析式为
.
(2)直接写出乙队在2≤x≤5的时间段内,
y关于x的函数解析式为
.
D
y=10x
y=20x-30
3.
已知点P(x,y)是第一象限内一次函数y=-x+6图象上的一点(点P不在坐标轴上),点A的坐标是(4,0),
?PAO的面积为S.
(1)求S与x的函数关系;
(2)求自变量x的取值范围.
解:(1)
∵点P(x,y)是第一象限内一次函数y=-x+6图象上的一点
(点P不在坐标轴上),点A的坐标是(4,0),
∴?PAO的面积为
S=
×4×(-x+6)=-2x+12,
(2)
∵点P在第一象限内,
∴0<x<6.
知识回顾
4.一次函数的应用
一次函数与一元一次方程、一元一次不等式、二元一次方程(组)的关系
一次函数的实际应用.
考点对接
D
1.
小亮从家步行到公交车站台,等公交车去学校。图中的折线表示小亮的行程S(km)与所花时间t(min)之间的函数关系。下列说法错误的是(
)。
A.
他离家共用了30min
B.
他等公交车时间为6min
C.
他步行的速度是100m/min
D.
公交车的速度是350/min
2.
“五一节”期间,申老师一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(时)之间的函数图象。
(1)求他们出发半小时时,离家多少千米。
(2)求出AB段图象的函数表达式。
(3)他们出发2小时时,离目的地还有多少千米。
(1)设OA段图象的函数表达式为y=k?x,将点(1.5,90)代入得
k?==
5=60,
∴OA段图象函数表达式为y=60x(0≤x≤1.5)
出发半小时,离家的距离y=60x×0.5=30(千米)。
(2)设AB段图象的函数表达式为y=k?x+b,将点A(1.5,90)与B(2.5,170)代入得
1.5k?+b=90
①,2.5k?+b=170,
解得:k?=80,b=-30,
则AB段图象的函数表达式为y=80x-30(1.5≤x≤2.5).
(3)当x=2时,代入AB段函数表达式得y=80x-30=80×2-30=130(千米),
离目的地还有170-130=40(千米)。
3.
手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式。方式A:以每分钟0.1元的价格按上网时间计费;方式B:除收月基费20元外,再以每分钟0.06元的价格按上网时间计费。假设某客户月手机上网的时间为x分钟,上网费用为y元。
(1)分别写出该客户按A、B两种方式的上网费y(元)与每月上网时间x(分钟)的函数关系式,并在图中的坐标系中画出这两个函数的图象。
(2)如何选择计费方式能使该客户上网费用更合算?
(1)由题意得:方式A:yA=0.1x,
方式B:yB=0.06x+20,
函数图象如图所示。
(2)如何选择计费方式能使该客户上网费用更合算?
(2)当yA=yB,即0.1x=0.06x+20时,解得:x=500;
当yA<yB,即0.1x<0.06x+20时,解得:x<500;
yA<yB,即0.1x<0.06x+20时,解得:x>500.
所以当月手机上网时间小于500分钟时,选择方式A上网更合算;当月手机上网时间等于500分钟时,选择方式A和方式B上网一样合算;当月手机上网时间大于500分钟时,选择方式B上网更合算。
随堂检测
1.若b>0,则一次函数y=-x+b的图象大致是(
)
2.下列函数中,对于任意实数x1,x2,当x1>x2时,满足y1<y2的是(
)
A.y=-3x+2
B.y=2x+1
C.y=2x2+1
D.y=-1/x
C
A
3.如图,直线l是一次函数y=kx+b的图象,如果点A(3,m)在直线l上,则m的值为(
)
A.-5
B.3/2
C.5/2
D.7
4.对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.例如:min={2,-1}=-1,若关于x的函数y=min{2x-1,-x+3},则该函数的最大值为(
)
A.2/3
B.1
C.4/3
D.5/3
C
D
5.将直线y=
x向上平移2个单位长度,平移后直线的解析式为
.
6.如图,直线y=kx+b交x轴于点A,交y轴于点B,
则不等式x(kx+b)<0的解集为
.
7.设点(-1,m)和点(1/2,n)是直线y=(k2-1)x+b
(0<k<1)上的两个点,则m,n的大小关系为
.
8.
如图,一次函数的图象与x轴、y轴分别相交于点A,B,将△AOB沿直线AB翻折得△ACB
.若C(
),则该
一次函数的解析式为
.
y=x+2
-3<x<0
m>n
y=-
x+
9.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
解
:(1)设一次函数的解析式为y=kx+b,
则-3=-2k+b
①,3=k+b
②,
由①、②得k=2,b=1,
∴函数的解析式为y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0时,y=1,当y=0时,x=-12,
此函数与x轴、y轴围成的三角形的面积为?×1×|-?|=?.
10.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地。设先发车辆行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系。根据图象解决以下问题。
(1)慢车的速度为
km/h,快车的速度为
km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300
km.
解:(2)慢车走完全程需要480÷80=6h,快车走完全程需要480÷120=4h,而慢车仅比快车早出发0.5h,故快车先到达乙地。图中点D的实际意义为快车到达了乙地,此时慢车已经行驶了4+0,5=4.5h,此时两车的距离为(80+120)×(4.5-2.7)=360km。
两车相距360km,点D的坐标为(4.5,360)。
80
120
10.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地。设先发车辆行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系。根据图象解决以下问题。
(1)慢车的速度为
km/h,快车的速度为
km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300
km.
解:(3)由题意可知两车有两次距离为300。
相遇前:(80+120)(x-0.5)=440-300,解得x=1.2;
相遇后:(80+120)(x-2.7)=300,解得x=4.2。
综上所述,当x=1.2或x=4.2时,两车之间的距离为300km。
80
120
1.三个概念:函数、正比例函数、一次函数;
2.一个性质:一次函数的性质;
3.一个应用:一次函数的应用;
课堂小结
再见
