2020-2021学年北师大版八年级数学下册:第三章《图形的平移与旋转》单元综合测试卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册:第三章《图形的平移与旋转》单元综合测试卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 467.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 17:32:13 | ||
图片预览



文档简介
北师版八年级数学下册
第3章 图形的平移与旋转
单元综合测试卷
(时间90分钟,满分120分)
一、选择题(共10小题,3
10=30)
1.在以下生活现象中,属于旋转变换的是( )
A.钟表的指针和钟摆的运动
B.站在电梯上的人的运动
C.坐在火车上睡觉的旅客
D.地下水位线逐年下降
2.在下列四个新能源汽车车标的设计图中,属于中心对称图形的是( )
3.在下列实例中,属于平移过程的个数有( )
①时针运行过程;②电梯上升过程;
③火车直线行驶过程;④地球自转过程;
⑤生产过程中传送带上的电视机的移动过程.
A、1个 B、2个 C、3个 D、4个
4.如图,在正方形ABCD中,AB=4,点O在AB上,且OB=1,点P是BC上一动点,连接OP,将线段OP绕点Q逆时针旋转90°得到线段OQ.要使点Q恰好落在AD上,则BP的长是( )
A.1
B.2
C.3
D.4
5.如图,将一个含30°角的Rt△ABC绕点A旋转,使得点B,A,C′在同一条直线上,则△ABC旋转的角度是( )
A.60°
B.90°
C.120°
D.150°
6.
如图,在Rt△ABC和Rt△ABD中,∠ADB=∠ACB=90°,∠BAC=30°,AB=4,AD=2,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是( )
A.2≤DC≤4
B.2≤DC≤4
C.2-2≤DC≤2
D.2-2≤DC≤2+2
7.如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42
B.96
C.84
D.48
8.如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M
B.点N
C.点P
D.点Q
9.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点B与其对应点B′之间的距离为( )
A.
B.3
C.4
D.5
10.如图,△DEC是由△ABC经过了如下的几何变换而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转90°得△A′B′C′,再以A′C′所在直线为对称轴作轴对称;③将△ABC向下向左各平移1个单位长度,再以AC的中点为中心作中心对称,其中正确的变换有( )
A.①②
B.①③
C.②③
D.①②③
二.填空题(共8小题,3
8=24)
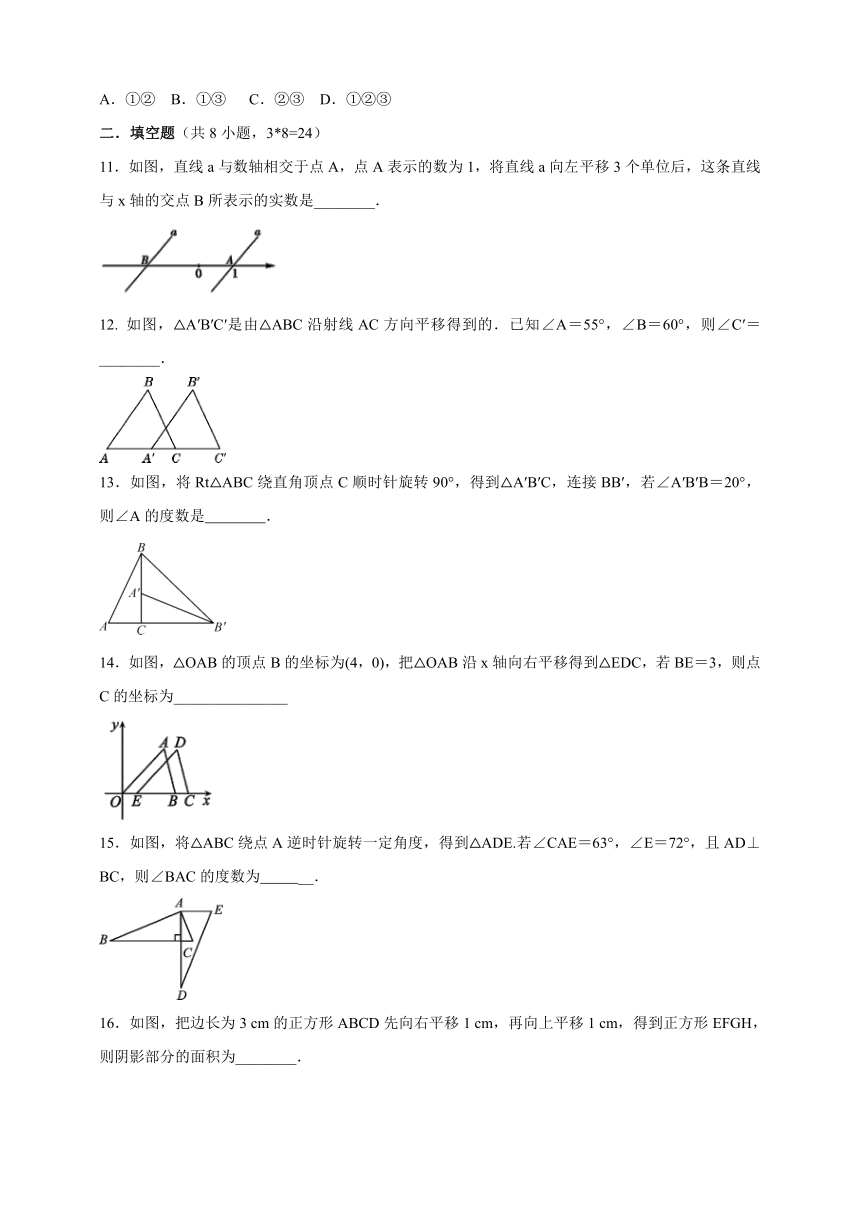
11.如图,直线a与数轴相交于点A,点A表示的数为1,将直线a向左平移3个单位后,这条直线与x轴的交点B所表示的实数是________.
12.
如图,△A′B′C′是由△ABC沿射线AC方向平移得到的.已知∠A=55°,∠B=60°,则∠C′=________.
13.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接BB′,若∠A′B′B=20°,则∠A的度数是
.
14.如图,△OAB的顶点B的坐标为(4,0),把△OAB沿x轴向右平移得到△EDC,若BE=3,则点C的坐标为_______________
15.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=63°,∠E=72°,且AD⊥BC,则∠BAC的度数为
__.
16.如图,把边长为3
cm的正方形ABCD先向右平移1
cm,再向上平移1
cm,得到正方形EFGH,则阴影部分的面积为________.
17.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为________.
18.如图,直线y=-x+4与x轴、y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是__________.
三.解答题(7小题,共66分)
19.(8分)
在如图1的方格纸中,每个小方格都是边长为1个单位长度的正方形,①②③均为顶点都在格点上的三角形(每个小方格的顶点叫格点).
(1)在图1中,①经过一次________变换(填“平移”“旋转”或“轴对称”)可以得到②;
(2)在图1中,③是可以由②经过一次旋转变换得到的,其旋转中心是点________;(填“A”“B”或“C”)
(3)在图2中画出①绕点A顺时针旋转90°后的④.
20.(8分)
如图,在△ABC中,∠ABC=90°,AB=4,AC=5,BC=3,将△ABC沿AD方向平移得到△DEF,已知AF=9.
(1)求△ABC平移的距离AD的长;
(2)求四边形AFEB的周长.
21.(8分)
如图,在直角坐标系xOy中,边长为2的等边三角形AOC的顶点A,O都在x轴上,顶点C在第二象限内,△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是2__个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴,△AOC绕原点O顺时针方向旋转得到△DOB,则旋转角度可以是120°;
(2)连接AD,交OC于点E,求∠AEO的度数.
22.(10分)
(1)在平面直角坐标系中找出点A(-3,4),B(-4,1),C(-1,1),D(-2,3)并将它们依次连接;
(2)将(1)中所画图形先向右平移4个单位,再向下平移3个单位,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?
23.(10分)
如图,点P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P到点P′的距离;
(2)求∠APB的度数.
24.(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
25.(12分)
如图,固定一块三角板,另一块三角板按图示开始平移至两条较大直角边重合时停止.(两个同学为一组,利用30°角的三角板作图形的平移运动)
(1)观察平移过程中的重叠部分是什么图形?你能把它画出来吗?
(2)分别求出平移距离为4
cm或10
cm时,重叠部分的面积;
(3)若平移的距离为x
cm,当x__________时,重叠部分为三角形;当x__________时,重叠部分为五边形.
参考答案
1-5ADCCD
6-10DDBCA
11.
-2
12.65°
13.
65°
14.
(5,0)
15.
81°
16.4
cm2
17.2cm
18.
(7,3)
19.
解:(1)平移 (2)A (3)图略.
20.
解:(1)由平移的性质,得AC=DF,∴AD=AF-DF=9-5=4.
(2)由平移的性质,得BE=AD=4,EF=BC=3,∴四边形AFEB的周长=AF+FE+EB+BA=20.
21.
解:(1);2;y轴;120°
(2)∵△AOC和△DOB是能够重合的等边三角形,∴AO=DO,∠AOC=∠COD=60°,∴OE⊥AD,∴∠AEO=90°.
22.
解:(1)画图略 (2)画图略 (3)将A点与它的对应点A′连接起来,则AA′==5,∴将(1)中所画图形沿A到A′的方向平移5个单位长度得到(2)中所画图形.四边形A′B′C′D′与四边形ABCD相比,对应点的横坐标分别增加了4,纵坐标分别减少了3
23.
解:(1)连接PP′,图略.由旋转的性质,得AP=AP′,∠PAP′=∠BAC=60°.∴△APP′为等边三角形,∴PP′=PA=6.(2)由(1)知,∠APP′=60°,由旋转性质,得BP′=CP=10,在△BPP′中,BP2+PP′2=82+62=102=BP′2,∴△BPP′为直角三角形,且∠BPP′=90°,∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
24.
(1)解:补全图形,如图所示.
(2)证明:由旋转的性质得:∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°.∵∠ACB=90°,∴∠DCE+∠BCD=90°.∴∠ECF=∠BCD.∵EF∥DC,∴∠EFC+∠DCF=180°.∴∠EFC=90°,在△BDC和△EFC中,
∴△BDC≌△EFC(SAS).∴∠BDC=∠EFC=90°.
25.
解:(1)平移过程中的重叠部分是三角形或五边形,如图①②
(2)当平移距离为4
cm时,重叠部分是三角形OAA′,如图③,此时AA′=4
cm.∵∠OAA′=∠OA′A=60°,∴△OAA′是等边三角形.∴S△OAA′=4(cm2).当平移距离为10
cm时,重叠部分是五边形ODC′CE,如图④,此时AA′=10
cm.∵AC=A′C′=7
cm,∴A′C=AC′=3
cm.∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,∴C′D=CE=3
cm,∴S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=×102-×3×3×2=16(cm2)
(3)当x≤7时,重叠部分为三角形,当721世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
第3章 图形的平移与旋转
单元综合测试卷
(时间90分钟,满分120分)
一、选择题(共10小题,3
10=30)
1.在以下生活现象中,属于旋转变换的是( )
A.钟表的指针和钟摆的运动
B.站在电梯上的人的运动
C.坐在火车上睡觉的旅客
D.地下水位线逐年下降
2.在下列四个新能源汽车车标的设计图中,属于中心对称图形的是( )
3.在下列实例中,属于平移过程的个数有( )
①时针运行过程;②电梯上升过程;
③火车直线行驶过程;④地球自转过程;
⑤生产过程中传送带上的电视机的移动过程.
A、1个 B、2个 C、3个 D、4个
4.如图,在正方形ABCD中,AB=4,点O在AB上,且OB=1,点P是BC上一动点,连接OP,将线段OP绕点Q逆时针旋转90°得到线段OQ.要使点Q恰好落在AD上,则BP的长是( )
A.1
B.2
C.3
D.4
5.如图,将一个含30°角的Rt△ABC绕点A旋转,使得点B,A,C′在同一条直线上,则△ABC旋转的角度是( )
A.60°
B.90°
C.120°
D.150°
6.
如图,在Rt△ABC和Rt△ABD中,∠ADB=∠ACB=90°,∠BAC=30°,AB=4,AD=2,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是( )
A.2≤DC≤4
B.2≤DC≤4
C.2-2≤DC≤2
D.2-2≤DC≤2+2
7.如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42
B.96
C.84
D.48
8.如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M
B.点N
C.点P
D.点Q
9.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点B与其对应点B′之间的距离为( )
A.
B.3
C.4
D.5
10.如图,△DEC是由△ABC经过了如下的几何变换而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转90°得△A′B′C′,再以A′C′所在直线为对称轴作轴对称;③将△ABC向下向左各平移1个单位长度,再以AC的中点为中心作中心对称,其中正确的变换有( )
A.①②
B.①③
C.②③
D.①②③
二.填空题(共8小题,3
8=24)
11.如图,直线a与数轴相交于点A,点A表示的数为1,将直线a向左平移3个单位后,这条直线与x轴的交点B所表示的实数是________.
12.
如图,△A′B′C′是由△ABC沿射线AC方向平移得到的.已知∠A=55°,∠B=60°,则∠C′=________.
13.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接BB′,若∠A′B′B=20°,则∠A的度数是
.
14.如图,△OAB的顶点B的坐标为(4,0),把△OAB沿x轴向右平移得到△EDC,若BE=3,则点C的坐标为_______________
15.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=63°,∠E=72°,且AD⊥BC,则∠BAC的度数为
__.
16.如图,把边长为3
cm的正方形ABCD先向右平移1
cm,再向上平移1
cm,得到正方形EFGH,则阴影部分的面积为________.
17.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为________.
18.如图,直线y=-x+4与x轴、y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是__________.
三.解答题(7小题,共66分)
19.(8分)
在如图1的方格纸中,每个小方格都是边长为1个单位长度的正方形,①②③均为顶点都在格点上的三角形(每个小方格的顶点叫格点).
(1)在图1中,①经过一次________变换(填“平移”“旋转”或“轴对称”)可以得到②;
(2)在图1中,③是可以由②经过一次旋转变换得到的,其旋转中心是点________;(填“A”“B”或“C”)
(3)在图2中画出①绕点A顺时针旋转90°后的④.
20.(8分)
如图,在△ABC中,∠ABC=90°,AB=4,AC=5,BC=3,将△ABC沿AD方向平移得到△DEF,已知AF=9.
(1)求△ABC平移的距离AD的长;
(2)求四边形AFEB的周长.
21.(8分)
如图,在直角坐标系xOy中,边长为2的等边三角形AOC的顶点A,O都在x轴上,顶点C在第二象限内,△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是2__个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴,△AOC绕原点O顺时针方向旋转得到△DOB,则旋转角度可以是120°;
(2)连接AD,交OC于点E,求∠AEO的度数.
22.(10分)
(1)在平面直角坐标系中找出点A(-3,4),B(-4,1),C(-1,1),D(-2,3)并将它们依次连接;
(2)将(1)中所画图形先向右平移4个单位,再向下平移3个单位,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?
23.(10分)
如图,点P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P到点P′的距离;
(2)求∠APB的度数.
24.(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
25.(12分)
如图,固定一块三角板,另一块三角板按图示开始平移至两条较大直角边重合时停止.(两个同学为一组,利用30°角的三角板作图形的平移运动)
(1)观察平移过程中的重叠部分是什么图形?你能把它画出来吗?
(2)分别求出平移距离为4
cm或10
cm时,重叠部分的面积;
(3)若平移的距离为x
cm,当x__________时,重叠部分为三角形;当x__________时,重叠部分为五边形.
参考答案
1-5ADCCD
6-10DDBCA
11.
-2
12.65°
13.
65°
14.
(5,0)
15.
81°
16.4
cm2
17.2cm
18.
(7,3)
19.
解:(1)平移 (2)A (3)图略.
20.
解:(1)由平移的性质,得AC=DF,∴AD=AF-DF=9-5=4.
(2)由平移的性质,得BE=AD=4,EF=BC=3,∴四边形AFEB的周长=AF+FE+EB+BA=20.
21.
解:(1);2;y轴;120°
(2)∵△AOC和△DOB是能够重合的等边三角形,∴AO=DO,∠AOC=∠COD=60°,∴OE⊥AD,∴∠AEO=90°.
22.
解:(1)画图略 (2)画图略 (3)将A点与它的对应点A′连接起来,则AA′==5,∴将(1)中所画图形沿A到A′的方向平移5个单位长度得到(2)中所画图形.四边形A′B′C′D′与四边形ABCD相比,对应点的横坐标分别增加了4,纵坐标分别减少了3
23.
解:(1)连接PP′,图略.由旋转的性质,得AP=AP′,∠PAP′=∠BAC=60°.∴△APP′为等边三角形,∴PP′=PA=6.(2)由(1)知,∠APP′=60°,由旋转性质,得BP′=CP=10,在△BPP′中,BP2+PP′2=82+62=102=BP′2,∴△BPP′为直角三角形,且∠BPP′=90°,∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
24.
(1)解:补全图形,如图所示.
(2)证明:由旋转的性质得:∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°.∵∠ACB=90°,∴∠DCE+∠BCD=90°.∴∠ECF=∠BCD.∵EF∥DC,∴∠EFC+∠DCF=180°.∴∠EFC=90°,在△BDC和△EFC中,
∴△BDC≌△EFC(SAS).∴∠BDC=∠EFC=90°.
25.
解:(1)平移过程中的重叠部分是三角形或五边形,如图①②
(2)当平移距离为4
cm时,重叠部分是三角形OAA′,如图③,此时AA′=4
cm.∵∠OAA′=∠OA′A=60°,∴△OAA′是等边三角形.∴S△OAA′=4(cm2).当平移距离为10
cm时,重叠部分是五边形ODC′CE,如图④,此时AA′=10
cm.∵AC=A′C′=7
cm,∴A′C=AC′=3
cm.∵∠A=∠A′=60°,∠AC′D=∠A′CE=90°,∴C′D=CE=3
cm,∴S五边形ODC′CE=S△OAA′-S△AC′D-S△A′CE=×102-×3×3×2=16(cm2)
(3)当x≤7时,重叠部分为三角形,当7
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
