17.1 勾股定理(第2课时) 知识点导学导练+检测(含答案)
文档属性
| 名称 | 17.1 勾股定理(第2课时) 知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 143.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 17:43:26 | ||
图片预览


文档简介
17.1勾股定理(第2课时)
A 双基导学导练
知识点1:利用勾股定理进行计算
1、一直角三角形的斜边比一直角边长2,另一直角边长为6,那么斜边长为( )
A.4 B. 8 C.10 D.12
如果一个直角三角形有一个锐角为30°,斜边长为1cm,那么两条直角边的和为( )
A.falsecm B. falsecm C.falsecm D.falsecm
3、下列命题中,真命题是( ).
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.如果三角形三边长的比为1:2:3,那么这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为?false
4、如图,在直线false上有三个正方形,若左右两正方形的面积分别为5和11,则中间正方形的面积为( )
A.12 B. 15 C.16 D.25
5、(1)直角三角形的三边长为连续偶数,则其周长
(2)直角三角形的周长为12cm,斜边的长为5cm。则其面积为 cm2.
6、等腰三角形的顶角为120°,腰长为6cm,则此等腰三角形的面积为 cm2.
7、小明想知道旗杆的高度,他发现旗杆顶端的绳子垂到地面还多出1米,他把绳子的下端往外拉开5米后,发现下端刚好接触地面,求旗杆的高度。
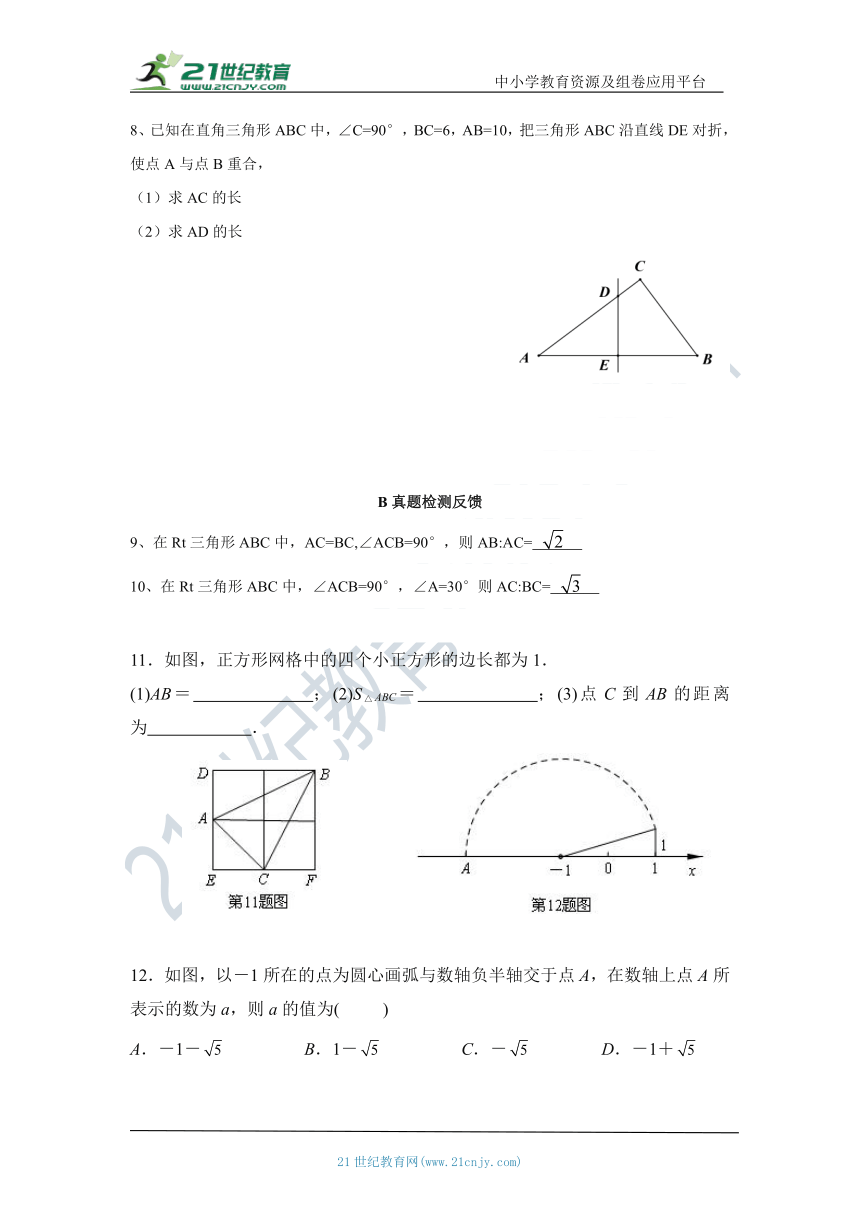
8、已知在直角三角形ABC中,∠C=90°,BC=6,AB=10,把三角形ABC沿直线DE对折,使点A与点B重合,
求AC的长
求AD的长
B真题检测反馈
9、在Rt三角形ABC中,AC=BC,∠ACB=90°,则AB:AC= false
10、在Rt三角形ABC中,∠ACB=90°,∠A=30°则AC:BC= false
11.如图,正方形网格中的四个小正方形的边长都为1.
(1)AB= ;(2)S△ABC= ;(3)点C到AB的距离为 .
12.如图,以-1所在的点为圆心画弧与数轴负半轴交于点A,在数轴上点A所表示的数为a,则a的值为( )
A.-1-false B.1-false C.-false D.-1+false
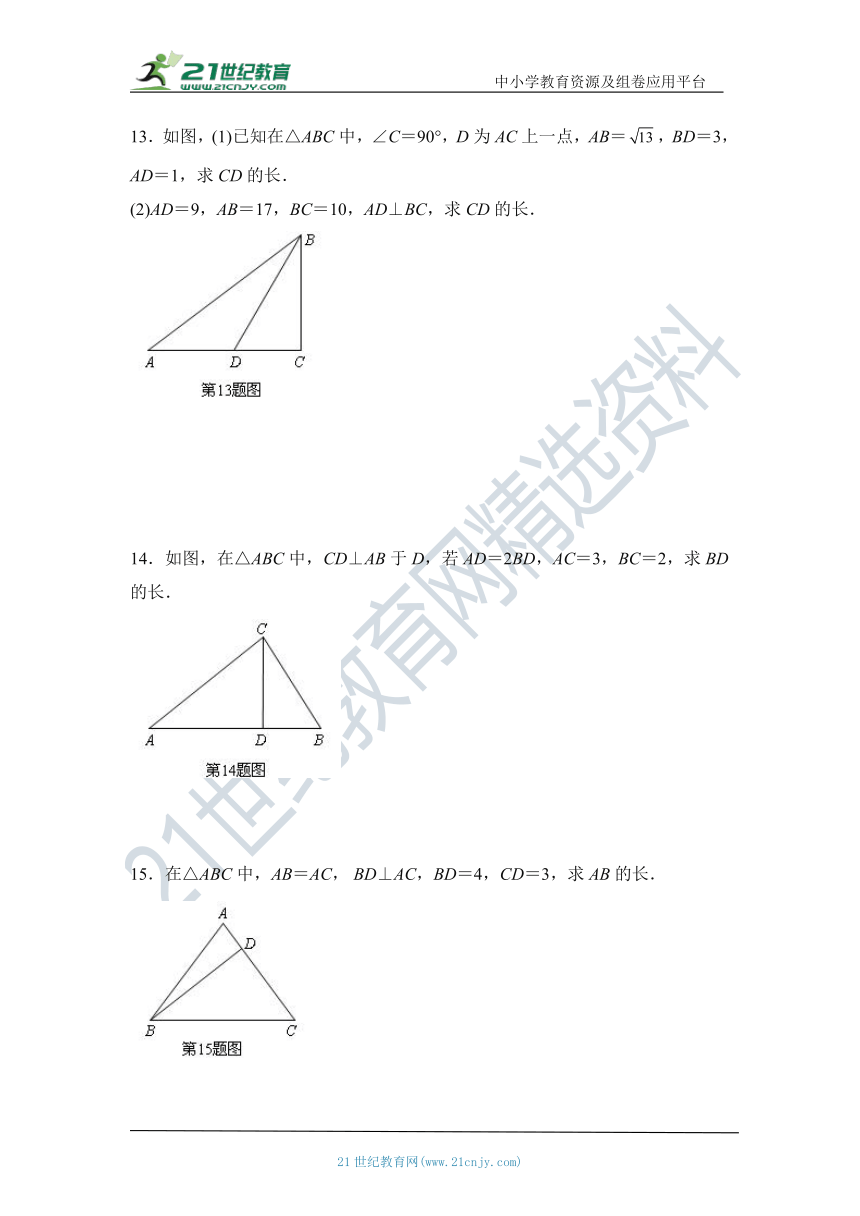
13.如图,(1)已知在△ABC中,∠C=90°,D为AC上一点,AB=false,BD=3,AD=1,求CD的长.
(2)AD=9,AB=17,BC=10,AD⊥BC,求CD的长.
14.如图,在△ABC中,CD⊥AB于D,若AD=2BD,AC=3,BC=2,求BD的长.
15.在△ABC中,AB=AC,?BD⊥AC,BD=4,CD=3,求AB的长.
创新拓展提升
16.直角三角形有一条直角边长为11,另外两边长是正整数,求它的周长.
17.1勾股定理(第2课时)
A 双基导学导练
知识点1:利用勾股定理进行计算
1、一直角三角形的斜边比一直角边长2,另一直角边长为6,那么斜边长为( C )
A.4 B. 8 C.10 D.12
2、如果一个直角三角形有一个锐角为30°,斜边长为1cm,那么两条直角边的和为(D)
A.falsecm B. falsecm C.falsecm D.falsecm
3、下列命题中,真命题是( D ).
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.如果三角形三边长的比为1:2:3,那么这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为?false
4、如图,在直线false上有三个正方形,若左右两正方形的面积分别为5和11,则中间正方形的面积为( C )
A.12 B. 15 C.16 D.25
5、(1)直角三角形的三边长为连续偶数,则其周长 24
(2)直角三角形的周长为12cm,斜边的长为5cm。则其面积为 6 cm2.
6、等腰三角形的顶角为120°,腰长为6cm,则此等腰三角形的面积为falsecm2.
7、小明想知道旗杆的高度,他发现旗杆顶端的绳子垂到地面还多出1米,他把绳子的下端往外拉开5米后,发现下端刚好接触地面,求旗杆的高度。
解:设旗杆的高AB为x米,则绳子AC的长为(x+1)米,
在Rt△ABC中,BC=5米,
AB2+BC2=AC2,
∴x2+52=(x+1)2,
解得x=12,
∴AB=12.
∴旗杆的高12米。
8、已知在直角三角形ABC中,∠C=90°,BC=6,AB=10,把三角形ABC沿直线DE对折,使点A与点B重合,
求AC的长
求AD的长
解:(1)AC=false
(2)AD=false
B真题检测反馈
9、在Rt三角形ABC中,AC=BC,∠ACB=90°,则AB:AC= false
10、在Rt三角形ABC中,∠ACB=90°,∠A=30°则AC:BC= false
11.如图,正方形网格中的四个小正方形的边长都为1.
(1)AB= ;(2)S△ABC= ;(3)点C到AB的距离为 .
【答案】(1)false;(2)false ;(3)false
12.如图,以-1所在的点为圆心画弧与数轴负半轴交于点A,在数轴上点A所表示的数为a,则a的值为( )
A.-1-false B.1-false C.-false D.-1+false
【答案】A
13.如图,(1)已知在△ABC中,∠C=90°,D为AC上一点,AB=false,BD=3,AD=1,求CD的长.
(2)AD=9,AB=17,BC=10,AD⊥BC,求CD的长.
【答案】解:(1)设CD=x ,∵BD2-CD2=AB2-AC2∴9-x2=13-(1+x)2,x=false即CD=false
(2)设CD=x ∴(x+9)2+102=172 ∴x=false-9 ,即DC=false-9
14.如图,在△ABC中,CD⊥AB于D,若AD=2BD,AC=3,BC=2,求BD的长.
【答案】解:∵AC2-AD2=BC2-BD2=CD2
设BD=x,AD=2x ,∴9-4x2=4-x2, x=false即BD=false.
15.在△ABC中,AB=AC,?BD⊥AC,BD=4,CD=3,求AB的长.
【答案】解:∵AB=AC,设AB=x,则AD=x-3
∵在Rt△ADB中,AB2=AD2+BD2 ∴x=16+(x-3)2,x=false 即AB=false.
创新拓展提升
16.直角三角形有一条直角边长为11,另外两边长是正整数,求它的周长.
【答案】解:设另外两边长分别为m,n(m>n)
∵m2-n2=112=121=(m+n)(m-n) ∴m+n=121,m-n=1,m=61,n=60.
∴它的周长为61+60+11=132
A 双基导学导练
知识点1:利用勾股定理进行计算
1、一直角三角形的斜边比一直角边长2,另一直角边长为6,那么斜边长为( )
A.4 B. 8 C.10 D.12
如果一个直角三角形有一个锐角为30°,斜边长为1cm,那么两条直角边的和为( )
A.falsecm B. falsecm C.falsecm D.falsecm
3、下列命题中,真命题是( ).
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.如果三角形三边长的比为1:2:3,那么这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为?false
4、如图,在直线false上有三个正方形,若左右两正方形的面积分别为5和11,则中间正方形的面积为( )
A.12 B. 15 C.16 D.25
5、(1)直角三角形的三边长为连续偶数,则其周长
(2)直角三角形的周长为12cm,斜边的长为5cm。则其面积为 cm2.
6、等腰三角形的顶角为120°,腰长为6cm,则此等腰三角形的面积为 cm2.
7、小明想知道旗杆的高度,他发现旗杆顶端的绳子垂到地面还多出1米,他把绳子的下端往外拉开5米后,发现下端刚好接触地面,求旗杆的高度。
8、已知在直角三角形ABC中,∠C=90°,BC=6,AB=10,把三角形ABC沿直线DE对折,使点A与点B重合,
求AC的长
求AD的长
B真题检测反馈
9、在Rt三角形ABC中,AC=BC,∠ACB=90°,则AB:AC= false
10、在Rt三角形ABC中,∠ACB=90°,∠A=30°则AC:BC= false
11.如图,正方形网格中的四个小正方形的边长都为1.
(1)AB= ;(2)S△ABC= ;(3)点C到AB的距离为 .
12.如图,以-1所在的点为圆心画弧与数轴负半轴交于点A,在数轴上点A所表示的数为a,则a的值为( )
A.-1-false B.1-false C.-false D.-1+false
13.如图,(1)已知在△ABC中,∠C=90°,D为AC上一点,AB=false,BD=3,AD=1,求CD的长.
(2)AD=9,AB=17,BC=10,AD⊥BC,求CD的长.
14.如图,在△ABC中,CD⊥AB于D,若AD=2BD,AC=3,BC=2,求BD的长.
15.在△ABC中,AB=AC,?BD⊥AC,BD=4,CD=3,求AB的长.
创新拓展提升
16.直角三角形有一条直角边长为11,另外两边长是正整数,求它的周长.
17.1勾股定理(第2课时)
A 双基导学导练
知识点1:利用勾股定理进行计算
1、一直角三角形的斜边比一直角边长2,另一直角边长为6,那么斜边长为( C )
A.4 B. 8 C.10 D.12
2、如果一个直角三角形有一个锐角为30°,斜边长为1cm,那么两条直角边的和为(D)
A.falsecm B. falsecm C.falsecm D.falsecm
3、下列命题中,真命题是( D ).
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.如果三角形三边长的比为1:2:3,那么这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为?false
4、如图,在直线false上有三个正方形,若左右两正方形的面积分别为5和11,则中间正方形的面积为( C )
A.12 B. 15 C.16 D.25
5、(1)直角三角形的三边长为连续偶数,则其周长 24
(2)直角三角形的周长为12cm,斜边的长为5cm。则其面积为 6 cm2.
6、等腰三角形的顶角为120°,腰长为6cm,则此等腰三角形的面积为falsecm2.
7、小明想知道旗杆的高度,他发现旗杆顶端的绳子垂到地面还多出1米,他把绳子的下端往外拉开5米后,发现下端刚好接触地面,求旗杆的高度。
解:设旗杆的高AB为x米,则绳子AC的长为(x+1)米,
在Rt△ABC中,BC=5米,
AB2+BC2=AC2,
∴x2+52=(x+1)2,
解得x=12,
∴AB=12.
∴旗杆的高12米。
8、已知在直角三角形ABC中,∠C=90°,BC=6,AB=10,把三角形ABC沿直线DE对折,使点A与点B重合,
求AC的长
求AD的长
解:(1)AC=false
(2)AD=false
B真题检测反馈
9、在Rt三角形ABC中,AC=BC,∠ACB=90°,则AB:AC= false
10、在Rt三角形ABC中,∠ACB=90°,∠A=30°则AC:BC= false
11.如图,正方形网格中的四个小正方形的边长都为1.
(1)AB= ;(2)S△ABC= ;(3)点C到AB的距离为 .
【答案】(1)false;(2)false ;(3)false
12.如图,以-1所在的点为圆心画弧与数轴负半轴交于点A,在数轴上点A所表示的数为a,则a的值为( )
A.-1-false B.1-false C.-false D.-1+false
【答案】A
13.如图,(1)已知在△ABC中,∠C=90°,D为AC上一点,AB=false,BD=3,AD=1,求CD的长.
(2)AD=9,AB=17,BC=10,AD⊥BC,求CD的长.
【答案】解:(1)设CD=x ,∵BD2-CD2=AB2-AC2∴9-x2=13-(1+x)2,x=false即CD=false
(2)设CD=x ∴(x+9)2+102=172 ∴x=false-9 ,即DC=false-9
14.如图,在△ABC中,CD⊥AB于D,若AD=2BD,AC=3,BC=2,求BD的长.
【答案】解:∵AC2-AD2=BC2-BD2=CD2
设BD=x,AD=2x ,∴9-4x2=4-x2, x=false即BD=false.
15.在△ABC中,AB=AC,?BD⊥AC,BD=4,CD=3,求AB的长.
【答案】解:∵AB=AC,设AB=x,则AD=x-3
∵在Rt△ADB中,AB2=AD2+BD2 ∴x=16+(x-3)2,x=false 即AB=false.
创新拓展提升
16.直角三角形有一条直角边长为11,另外两边长是正整数,求它的周长.
【答案】解:设另外两边长分别为m,n(m>n)
∵m2-n2=112=121=(m+n)(m-n) ∴m+n=121,m-n=1,m=61,n=60.
∴它的周长为61+60+11=132
