17.1 勾股定理(第1课时) 知识点导学导练+检测(含答案)
文档属性
| 名称 | 17.1 勾股定理(第1课时) 知识点导学导练+检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 00:00:00 | ||
图片预览


文档简介
17.1 勾股定理(第1课时)
A双基导学导练
知识点1:勾股定理:直角三角形两直角边的平方和等于斜边的平方
直角三角形的两直角边长分别为6cm和8cm,则斜边长为( )
A,10cm B,3cm C,4cm D,5cm
等腰直角三角形的直角边为2,则斜边长为( )
A,false B,2false C,1 D,2
在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对的边为a,b,c,则下列结论正确的是( )
A,b2+c2=a2 B ,a ?-b2=c2
C,a2=c2-b2 D, a ?-c2=b2
4.一个三角形的三边为三个连续偶数,则它的三条边分别为( )
A,2.4.6 B,4.6.8 C,6.8.10 D,3.4.5
5.已知等边三角形的边长为2,则等边三角形的面积为( )
A,23 B,3 C,1 D,2
6.在△ABC中,∠C等于90°,∠A等于30°,则其三边a:b:c的比为
7.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,BC的边长是
8.如图,△ABC中,∠ABC=90°,以△ABC的各边长为边在△ABC外作三个正方形,S1,S2,S3,分别表示这三个正方形的面积,若S1=70,S3=150,则S2= .
9.长方形的周长为14cm,长为4cm,则它的对角线为 cm.
10.如图,一旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处,则旗杆折断之前共有 米高。
11.如图,在水塔O的东北方向40m处有一水电站A,在水塔的东南方向30m处有一建筑地B,在AB之间铺一条笔直的输水管,则水管AB的长度为
m.
B真题检测反馈
12.平面直角坐标系中,已知点A(-3,-4),则线段OA的长为 。
13.等腰三角形腰长为10,底边长为12,则底边中线长为 ,面积为 。
14.在Rt△ABC中,∠C=90°,AC=4,周长为12,则斜边AB的长
为 。
15.如图所示,矩形纸片ABCD中,AB=4,AD=3,折叠纸片,使AD边与对角线BD重合,折痕为DG,求A`B及AG的长。
16.如图,在Rt△ABC中,∠ABC=90°,D为AC边的中点,过D点作DE垂直DF,交AB与E,交BC与F,若AE=4,FC=3,求EF的长。
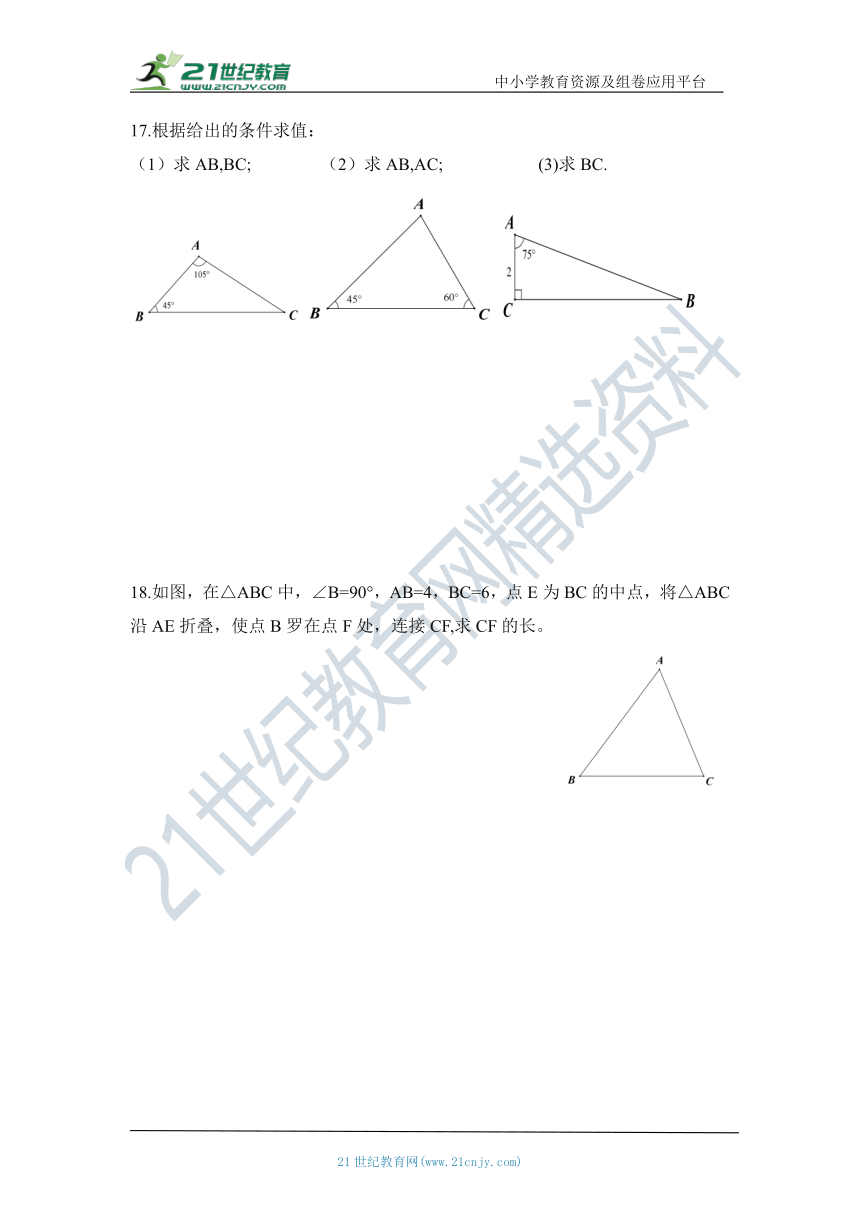
17.根据给出的条件求值:
(1)求AB,BC; (2)求AB,AC; (3)求BC.
18.如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABC沿AE折叠,使点B罗在点F处,连接CF,求CF的长。
C创新拓展提升
19、如图,在三角形ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将三角形ABE沿AF折叠,使点B落在点F处,链接CF,求CF的长。
17.1 勾股定理(第1课时)
A双基导学导练
知识点1:勾股定理:直角三角形两直角边的平方和等于斜边的平方
直角三角形的两直角边长分别为6cm和8cm,则斜边长为( A )
A,10cm B,3cm C,4cm D,5cm
等腰直角三角形的直角边为2,则斜边长为( B )
A,false B,2false C,1 D,2
在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对的边为a,b,c,则下列结论正确的是( C )
A,b2+c2=a2 B ,a ?-b2=c2
C,a2=c2-b2 D, a ?-c2=b2
4.一个三角形的三边为三个连续偶数,则它的三条边分别为( C )
A,2.4.6 B,4.6.8 C,6.8.10 D,3.4.5
5.已知等边三角形的边长为2,则等边三角形的面积为( B )
A,23 B,3 C,1 D,2
6.在△ABC中,∠C等于90°,∠A等于30°,则其三边a:b:c的比为 false
7.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,BC的边长是 false
8.如图,△ABC中,∠ABC=90°,以△ABC的各边长为边在△ABC外作三个正方形,S1,S2,S3,分别表示这三个正方形的面积,若S1=70,S3=150,则S2= 80 .
9.长方形的周长为14cm,长为4cm,则它的对角线为 5 cm.
10.如图,一旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处,则旗杆折断之前共有 18 米高。
11.如图,在水塔O的东北方向40m处有一水电站A,在水塔的东南方向30m处有一建筑地B,在AB之间铺一条笔直的输水管,则水管AB的长度为 50 m.
B真题检测反馈
12.平面直角坐标系中,已知点A(-3,-4),则线段OA的长为 5 。
13.等腰三角形腰长为10,底边长为12,则底边中线长为 8 ,面积为 48 。
14.在Rt△ABC中,∠C=90°,AC=4,周长为12,则斜边AB的长
为 5 。
15.如图所示,矩形纸片ABCD中,AB=4,AD=3,折叠纸片,使AD边与对角线BD重合,折痕为DG,求A`B及AG的长。
解:A’B=2,AG=false
16.如图,在Rt△ABC中,∠ABC=90°,D为AC边的中点,过D点作DE垂直DF,交AB与E,交BC与F,若AE=4,FC=3,求EF的长。
解:EF=5
17.根据给出的条件求值:
(1)求AB,BC; (2)求AB,AC; (3)求BC.
解:(1)AB=false (2) 解:AB=false (3) 解:BC=false
BC=false AC=4
18.如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABC沿AE折叠,使点B罗在点F处,连接CF,求CF的长。
解:AD=12
C创新拓展提升
19、如图,在三角形ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将三角形ABE沿AF折叠,使点B落在点F处,链接CF,求CF的长。
解:CF=false
A双基导学导练
知识点1:勾股定理:直角三角形两直角边的平方和等于斜边的平方
直角三角形的两直角边长分别为6cm和8cm,则斜边长为( )
A,10cm B,3cm C,4cm D,5cm
等腰直角三角形的直角边为2,则斜边长为( )
A,false B,2false C,1 D,2
在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对的边为a,b,c,则下列结论正确的是( )
A,b2+c2=a2 B ,a ?-b2=c2
C,a2=c2-b2 D, a ?-c2=b2
4.一个三角形的三边为三个连续偶数,则它的三条边分别为( )
A,2.4.6 B,4.6.8 C,6.8.10 D,3.4.5
5.已知等边三角形的边长为2,则等边三角形的面积为( )
A,23 B,3 C,1 D,2
6.在△ABC中,∠C等于90°,∠A等于30°,则其三边a:b:c的比为
7.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,BC的边长是
8.如图,△ABC中,∠ABC=90°,以△ABC的各边长为边在△ABC外作三个正方形,S1,S2,S3,分别表示这三个正方形的面积,若S1=70,S3=150,则S2= .
9.长方形的周长为14cm,长为4cm,则它的对角线为 cm.
10.如图,一旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处,则旗杆折断之前共有 米高。
11.如图,在水塔O的东北方向40m处有一水电站A,在水塔的东南方向30m处有一建筑地B,在AB之间铺一条笔直的输水管,则水管AB的长度为
m.
B真题检测反馈
12.平面直角坐标系中,已知点A(-3,-4),则线段OA的长为 。
13.等腰三角形腰长为10,底边长为12,则底边中线长为 ,面积为 。
14.在Rt△ABC中,∠C=90°,AC=4,周长为12,则斜边AB的长
为 。
15.如图所示,矩形纸片ABCD中,AB=4,AD=3,折叠纸片,使AD边与对角线BD重合,折痕为DG,求A`B及AG的长。
16.如图,在Rt△ABC中,∠ABC=90°,D为AC边的中点,过D点作DE垂直DF,交AB与E,交BC与F,若AE=4,FC=3,求EF的长。
17.根据给出的条件求值:
(1)求AB,BC; (2)求AB,AC; (3)求BC.
18.如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABC沿AE折叠,使点B罗在点F处,连接CF,求CF的长。
C创新拓展提升
19、如图,在三角形ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将三角形ABE沿AF折叠,使点B落在点F处,链接CF,求CF的长。
17.1 勾股定理(第1课时)
A双基导学导练
知识点1:勾股定理:直角三角形两直角边的平方和等于斜边的平方
直角三角形的两直角边长分别为6cm和8cm,则斜边长为( A )
A,10cm B,3cm C,4cm D,5cm
等腰直角三角形的直角边为2,则斜边长为( B )
A,false B,2false C,1 D,2
在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对的边为a,b,c,则下列结论正确的是( C )
A,b2+c2=a2 B ,a ?-b2=c2
C,a2=c2-b2 D, a ?-c2=b2
4.一个三角形的三边为三个连续偶数,则它的三条边分别为( C )
A,2.4.6 B,4.6.8 C,6.8.10 D,3.4.5
5.已知等边三角形的边长为2,则等边三角形的面积为( B )
A,23 B,3 C,1 D,2
6.在△ABC中,∠C等于90°,∠A等于30°,则其三边a:b:c的比为 false
7.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,BC的边长是 false
8.如图,△ABC中,∠ABC=90°,以△ABC的各边长为边在△ABC外作三个正方形,S1,S2,S3,分别表示这三个正方形的面积,若S1=70,S3=150,则S2= 80 .
9.长方形的周长为14cm,长为4cm,则它的对角线为 5 cm.
10.如图,一旗杆在离地面5m处折断,旗杆顶部落在离旗杆底部12m处,则旗杆折断之前共有 18 米高。
11.如图,在水塔O的东北方向40m处有一水电站A,在水塔的东南方向30m处有一建筑地B,在AB之间铺一条笔直的输水管,则水管AB的长度为 50 m.
B真题检测反馈
12.平面直角坐标系中,已知点A(-3,-4),则线段OA的长为 5 。
13.等腰三角形腰长为10,底边长为12,则底边中线长为 8 ,面积为 48 。
14.在Rt△ABC中,∠C=90°,AC=4,周长为12,则斜边AB的长
为 5 。
15.如图所示,矩形纸片ABCD中,AB=4,AD=3,折叠纸片,使AD边与对角线BD重合,折痕为DG,求A`B及AG的长。
解:A’B=2,AG=false
16.如图,在Rt△ABC中,∠ABC=90°,D为AC边的中点,过D点作DE垂直DF,交AB与E,交BC与F,若AE=4,FC=3,求EF的长。
解:EF=5
17.根据给出的条件求值:
(1)求AB,BC; (2)求AB,AC; (3)求BC.
解:(1)AB=false (2) 解:AB=false (3) 解:BC=false
BC=false AC=4
18.如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABC沿AE折叠,使点B罗在点F处,连接CF,求CF的长。
解:AD=12
C创新拓展提升
19、如图,在三角形ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将三角形ABE沿AF折叠,使点B落在点F处,链接CF,求CF的长。
解:CF=false
