第十八章 平行四边形章末复习: 微专题2 三角形中位线(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习: 微专题2 三角形中位线(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 00:00:00 | ||
图片预览


文档简介
微专题2三角形中位线
1.如图,已知E为□ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F,G,连接AC交BD于点O,连接OF.求证:
(1)△ABF≌△ECF;
(2)AB=2OF.
2.如图,BD、CE分别是△ABC的中线,相交于0,M为OB的中点,N为OC的中点,求证:MN∥DE.
3.如图,□ABCD中,对角线AC,BD相交于点O,E在直线AB上,且AE=AD,AF⊥ED于F,若□ABCD的周长为20,求OF的长.
4.如图,在□BCFD的对角线CD的延长线上取一点E,连接FE并延长到4点,使EA=EF,连接AB,求证:
CE∥AB.
5.如图,AB=BC,DC=DE,∠ABC=∠CDE=90°,D、B、C在一条直线上,F为AE的中点.
(1)求证:BF∥CE;
(2)若AB=2,DE=5,求BF的长.
lefttop
false6.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=false(AC-AB);
(2)若AD=6,BD=8,DM=2,求AC的长。
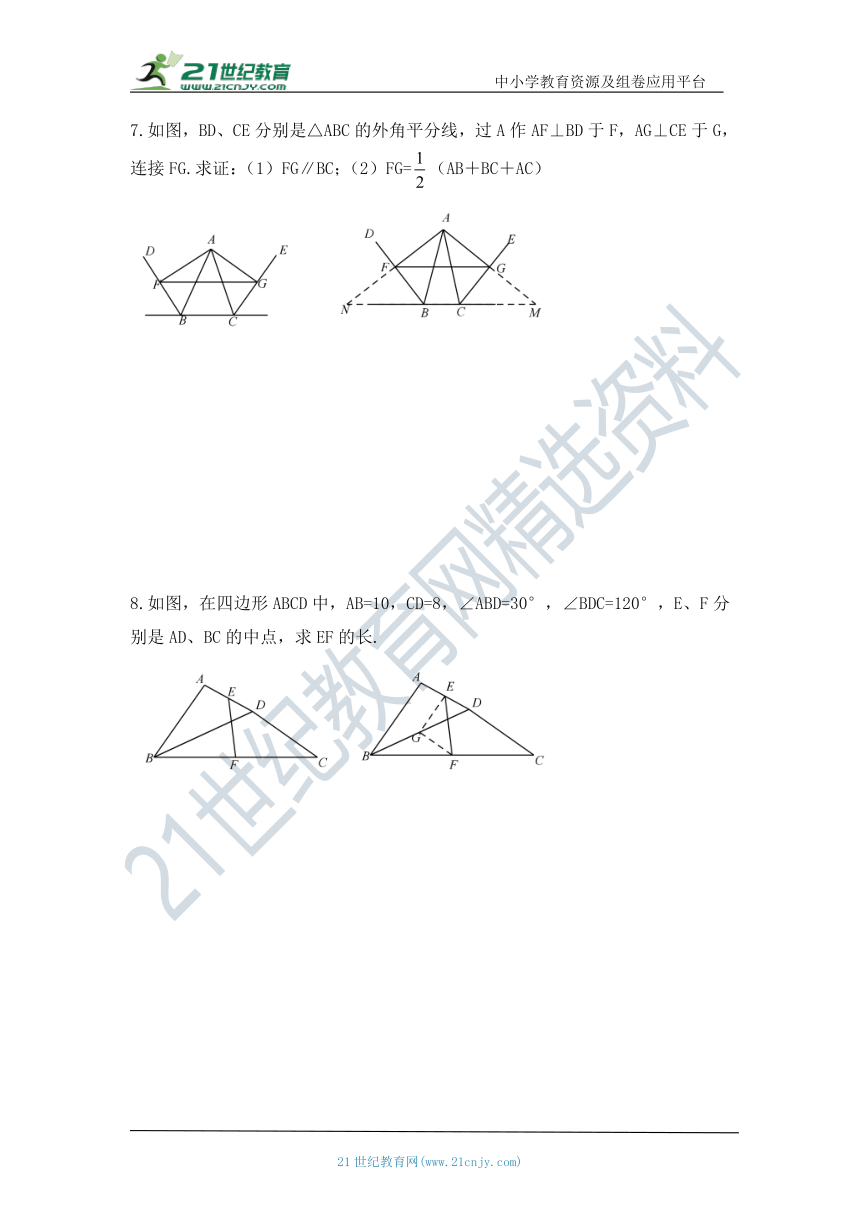
7.如图,BD、CE分别是△ABC的外角平分线,过A作AF⊥BD于F,AG⊥CE于G,连接FG.求证:(1)FG∥BC;(2)FG=false(AB+BC+AC)
8.如图,在四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E、F分别是AD、BC的中点,求EF的长.
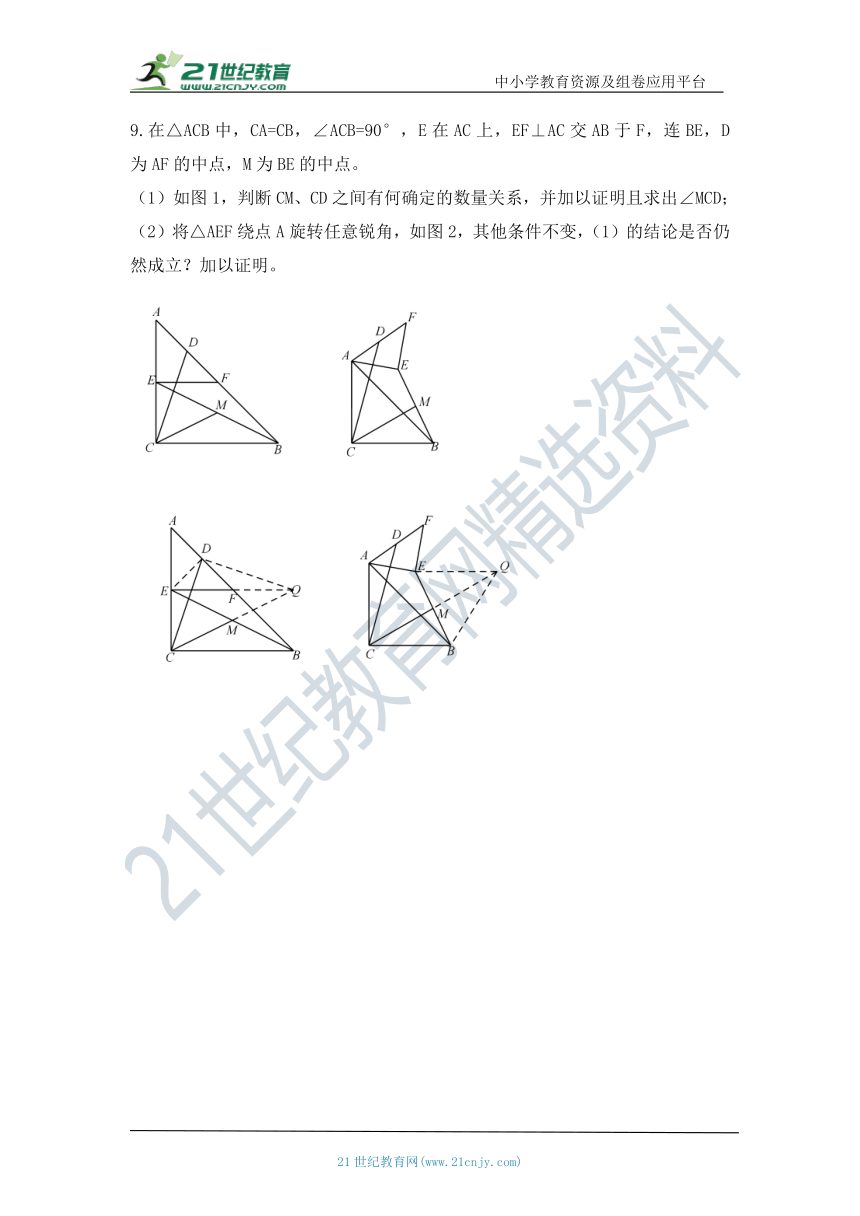
9.在△ACB中,CA=CB,∠ACB=90°,E在AC上,EF⊥AC交AB于F,连BE,D为AF的中点,M为BE的中点。
(1)如图1,判断CM、CD之间有何确定的数量关系,并加以证明且求出∠MCD;
(2)将△AEF绕点A旋转任意锐角,如图2,其他条件不变,(1)的结论是否仍然成立?加以证明。
微专题2三角形中位线
1.如图,已知E为□ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F,G,连接AC交BD于点O,连接OF.求证:
(1)△ABF≌△ECF;
(2)AB=2OF.
证明:(1)∵AB=CD=CE,∠E=∠BAF,∠AFB=∠CFE,∴△ABF≌△ECF(AAS)
(2)∵△ABF≌△ECF,∴BF=CF
又∵OA=OC,∴OFfalsefalseAB,∴AB=2OF.
2.如图,BD、CE分别是△ABC的中线,相交于0,M为OB的中点,N为OC的中点,求证:MN∥DE.
证明:∵ED、MN分别是△ABC、△OBC的中位线
∴ED∥BC,MN∥BC
∴MN∥DE.
3.如图,□ABCD中,对角线AC,BD相交于点O,E在直线AB上,且AE=AD,AF⊥ED于F,若□ABCD的周长为20,求OF的长.
解:∵AE=AD,AF⊥ED,∴EF=FD
又∵OB=OD
∴OF=false(AE+AB)=false×false×20=5
4.如图,在□BCFD的对角线CD的延长线上取一点E,连接FE并延长到4点,使EA=EF,连接AB,求证:
CE∥AB.
证明:连接BF交CD于点O
∵□BCFD,∴FO=BO
又∵FE=AE,∴EO为△FAB的中位线
∴CE∥AB.
5.如图,AB=BC,DC=DE,∠ABC=∠CDE=90°,D、B、C在一条直线上,F为AE的中点.
(1)求证:BF∥CE;
(2)若AB=2,DE=5,求BF的长.
lefttop
(1)证明:延长AB交CE于M,易证AB=BM,∵AF=FE,∴BFfalsefalseEM,∴BF∥CE.
(2)解:易证AC=2false=CM,CE=5false,∴EM=3false,∴BF=falseEM=false.
false6.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=false(AC-AB);
(2)若AD=6,BD=8,DM=2,求AC的长。
(1)证明:延长BD交AC于E
∵△ADB≌△ADE,∴BD=DE,AB=AE
又∵BM=MC,∴DM为△BCE的中位线
∴ DM=falseCE=false(AC-AB)
(2)解:易求AB=10,由(1)知AC-AB=2DM ∴ AC=14
7.如图,BD、CE分别是△ABC的外角平分线,过A作AF⊥BD于F,AG⊥CE于G,连接FG.求证:(1)FG∥BC;(2)FG=false(AB+BC+AC)
证明:(1)延长AF交BC于点N,延长AG交BC于点M,
可证△ABF≌△NBF,△AGC≌△MGC,
∴AF=FN,AG=GM,∴FG是△AMN的中位线,∴FG∥BC
(2)FG=falseMN=false(AB+BC+AC)
8.如图,在四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E、F分别是AD、BC的中点,求EF的长.
解:取BD的中点G,则EGfalsefalseAB,FGfalsefalseCD,∴EG=5,FG=4,∠EGD=∠ABD=30°,∠DGF=60°,∴∠EGF=90°,∴EF=false
9.在△ACB中,CA=CB,∠ACB=90°,E在AC上,EF⊥AC交AB于F,连BE,D为AF的中点,M为BE的中点。
(1)如图1,判断CM、CD之间有何确定的数量关系,并加以证明且求出∠MCD;
(2)将△AEF绕点A旋转任意锐角,如图2,其他条件不变,(1)的结论是否仍然成立?加以证明。
解:(1)延长EF交CM延长线于Q,连接DE、DQ,易证△EMQ≌△BMC, ∴EQ=CB,易得DE=AD, ∠DEQ=∠DAC=45°,∴△EDQ≌△ADC ∴DC=DQ,易得∠CDQ=90°,∴∠MCD=45°,CM=falseCQ而CQ=falseCD,∴CD=falseCM
(2)延长CM到Q,使CM=MQ,连QE,DE,DQ,∴易得△EMQ≌△BMC,∴EQ=CB=AC,又∵DE=DA,可证EQ∥CB,∴EQ⊥AC,∴∠DEQ=∠DAC,∴△DAC≌△DEQ,∴DQ=DC且DQ⊥DC,∴QC=falseCM
1.如图,已知E为□ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F,G,连接AC交BD于点O,连接OF.求证:
(1)△ABF≌△ECF;
(2)AB=2OF.
2.如图,BD、CE分别是△ABC的中线,相交于0,M为OB的中点,N为OC的中点,求证:MN∥DE.
3.如图,□ABCD中,对角线AC,BD相交于点O,E在直线AB上,且AE=AD,AF⊥ED于F,若□ABCD的周长为20,求OF的长.
4.如图,在□BCFD的对角线CD的延长线上取一点E,连接FE并延长到4点,使EA=EF,连接AB,求证:
CE∥AB.
5.如图,AB=BC,DC=DE,∠ABC=∠CDE=90°,D、B、C在一条直线上,F为AE的中点.
(1)求证:BF∥CE;
(2)若AB=2,DE=5,求BF的长.
lefttop
false6.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=false(AC-AB);
(2)若AD=6,BD=8,DM=2,求AC的长。
7.如图,BD、CE分别是△ABC的外角平分线,过A作AF⊥BD于F,AG⊥CE于G,连接FG.求证:(1)FG∥BC;(2)FG=false(AB+BC+AC)
8.如图,在四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E、F分别是AD、BC的中点,求EF的长.
9.在△ACB中,CA=CB,∠ACB=90°,E在AC上,EF⊥AC交AB于F,连BE,D为AF的中点,M为BE的中点。
(1)如图1,判断CM、CD之间有何确定的数量关系,并加以证明且求出∠MCD;
(2)将△AEF绕点A旋转任意锐角,如图2,其他条件不变,(1)的结论是否仍然成立?加以证明。
微专题2三角形中位线
1.如图,已知E为□ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F,G,连接AC交BD于点O,连接OF.求证:
(1)△ABF≌△ECF;
(2)AB=2OF.
证明:(1)∵AB=CD=CE,∠E=∠BAF,∠AFB=∠CFE,∴△ABF≌△ECF(AAS)
(2)∵△ABF≌△ECF,∴BF=CF
又∵OA=OC,∴OFfalsefalseAB,∴AB=2OF.
2.如图,BD、CE分别是△ABC的中线,相交于0,M为OB的中点,N为OC的中点,求证:MN∥DE.
证明:∵ED、MN分别是△ABC、△OBC的中位线
∴ED∥BC,MN∥BC
∴MN∥DE.
3.如图,□ABCD中,对角线AC,BD相交于点O,E在直线AB上,且AE=AD,AF⊥ED于F,若□ABCD的周长为20,求OF的长.
解:∵AE=AD,AF⊥ED,∴EF=FD
又∵OB=OD
∴OF=false(AE+AB)=false×false×20=5
4.如图,在□BCFD的对角线CD的延长线上取一点E,连接FE并延长到4点,使EA=EF,连接AB,求证:
CE∥AB.
证明:连接BF交CD于点O
∵□BCFD,∴FO=BO
又∵FE=AE,∴EO为△FAB的中位线
∴CE∥AB.
5.如图,AB=BC,DC=DE,∠ABC=∠CDE=90°,D、B、C在一条直线上,F为AE的中点.
(1)求证:BF∥CE;
(2)若AB=2,DE=5,求BF的长.
lefttop
(1)证明:延长AB交CE于M,易证AB=BM,∵AF=FE,∴BFfalsefalseEM,∴BF∥CE.
(2)解:易证AC=2false=CM,CE=5false,∴EM=3false,∴BF=falseEM=false.
false6.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=false(AC-AB);
(2)若AD=6,BD=8,DM=2,求AC的长。
(1)证明:延长BD交AC于E
∵△ADB≌△ADE,∴BD=DE,AB=AE
又∵BM=MC,∴DM为△BCE的中位线
∴ DM=falseCE=false(AC-AB)
(2)解:易求AB=10,由(1)知AC-AB=2DM ∴ AC=14
7.如图,BD、CE分别是△ABC的外角平分线,过A作AF⊥BD于F,AG⊥CE于G,连接FG.求证:(1)FG∥BC;(2)FG=false(AB+BC+AC)
证明:(1)延长AF交BC于点N,延长AG交BC于点M,
可证△ABF≌△NBF,△AGC≌△MGC,
∴AF=FN,AG=GM,∴FG是△AMN的中位线,∴FG∥BC
(2)FG=falseMN=false(AB+BC+AC)
8.如图,在四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E、F分别是AD、BC的中点,求EF的长.
解:取BD的中点G,则EGfalsefalseAB,FGfalsefalseCD,∴EG=5,FG=4,∠EGD=∠ABD=30°,∠DGF=60°,∴∠EGF=90°,∴EF=false
9.在△ACB中,CA=CB,∠ACB=90°,E在AC上,EF⊥AC交AB于F,连BE,D为AF的中点,M为BE的中点。
(1)如图1,判断CM、CD之间有何确定的数量关系,并加以证明且求出∠MCD;
(2)将△AEF绕点A旋转任意锐角,如图2,其他条件不变,(1)的结论是否仍然成立?加以证明。
解:(1)延长EF交CM延长线于Q,连接DE、DQ,易证△EMQ≌△BMC, ∴EQ=CB,易得DE=AD, ∠DEQ=∠DAC=45°,∴△EDQ≌△ADC ∴DC=DQ,易得∠CDQ=90°,∴∠MCD=45°,CM=falseCQ而CQ=falseCD,∴CD=falseCM
(2)延长CM到Q,使CM=MQ,连QE,DE,DQ,∴易得△EMQ≌△BMC,∴EQ=CB=AC,又∵DE=DA,可证EQ∥CB,∴EQ⊥AC,∴∠DEQ=∠DAC,∴△DAC≌△DEQ,∴DQ=DC且DQ⊥DC,∴QC=falseCM
