18.1平行四边形(第4课时) 知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.1平行四边形(第4课时) 知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 18:01:02 | ||
图片预览



文档简介
18.1平行四边形(第4课时)
A 双基导学导练
知识点 三角形的中位线平行于三角形的第三边,且等于第三边的一半
1.如图,在□ABCD中,对角线AC、BD相交于O点,E为CD的中点,若OE=3cm,则AD=( )
A.3cm B.6cm C.9cm D.12cm
第1题图 第2题图 第3题图
2.如图,在△ABC中,D、E分别是边AC、BC的中点,AB=6,则DE= .
3.如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=124°,则
∠ANM= .
4.如图,△ABC中,D、E、F分别为AB、AC、BC的中点.
(1)图中平行四边形有 个;
(2)若AC=5,AB=10,BC=7,则△DEF的周长为 .
5.顺次连接任意四边形四边中点所得到的四边形为 .
6.如图所示,在△ABC中,D、E分别是AB、AC的中点,则BE是△ABC的 ,线段DE是△ABC的
.
第4题图 第6题图
第8题图 第10题图
已知三角形的三条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm.
8.如图,在△MBN中,BM=7,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,□ABCD的周长是 .
9.四边形的两条对角线长分别是14cm和10cm,顺次连接各边中点所得四边形的周长是
10.如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,则PM与PN的大小关系是 .
B真题检测反馈
11.如图,△ABC中,中线BD、CE交于点O,F、G分别为OB、OC的中点,求证:四边形DEFG为平行四边形.
12.如图,四边形ABCD中,∠A=90°,AB=3false,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,求EF长度的最大值.
13.如图所示,在四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并说明理由.
14.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
C 创新拓展提升
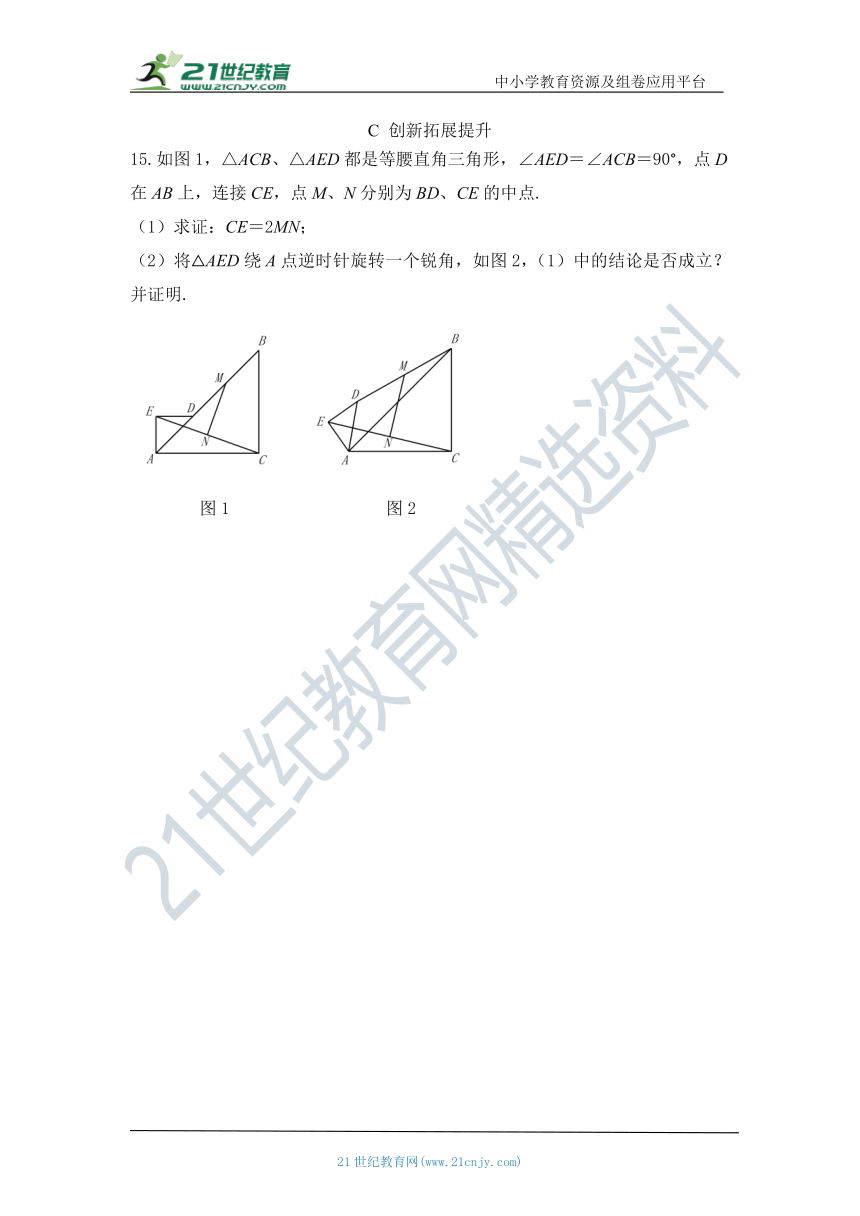
15.如图1,△ACB、△AED都是等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连接CE,点M、N分别为BD、CE的中点.
(1)求证:CE=2MN;
(2)将△AED绕A点逆时针旋转一个锐角,如图2,(1)中的结论是否成立?并证明.
图1 图2
18.1平行四边形(第4课时)
A 双基导学导练
知识点 三角形的中位线平行于三角形的第三边,且等于第三边的一半
1.如图,在□ABCD中,对角线AC、BD相交于O点,E为CD的中点,若OE=3cm,则AD=( )
A.3cm B.6cm C.9cm D.12cm
答案:B
第1题图 第2题图 第3题图
2.如图,在△ABC中,D、E分别是边AC、BC的中点,AB=6,则DE= .
答案:3
如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=124°,则
∠ANM= .
答案:56°
4.如图,△ABC中,D、E、F分别为AB、AC、BC的中点.
(1)图中平行四边形有 个;
(2)若AC=5,AB=10,BC=7,则△DEF的周长为 .
答案:3;11
5.顺次连接任意四边形四边中点所得到的四边形为 .
答案:平行四边形
6.如图所示,在△ABC中,D、E分别是AB、AC的中点,则BE是△ABC的 ,线段DE是△ABC的 .
答案:中线,中位线
第4题图 第6题图
第8题图 第10题图
7.已知三角形的三条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm.
答案:26
8.如图,在△MBN中,BM=7,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且
∠NDC=∠MDA,□ABCD的周长是 .
答案:14
9.四边形的两条对角线长分别是14cm和10cm,顺次连接各边中点所得四边形的周长是
答案:24cm
10.如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,则PM与PN的大小关系是 .
答案:PM=PM
B真题检测反馈
11.如图,△ABC中,中线BD、CE交于点O,F、G分别为OB、OC的中点,求证:四边形DEFG为平行四边形.
证明:∵FO=FB, GO=GC,∴FG∥BC且FG=falseBC
∵AE=EB AD=DC,∴ED∥BC且ED=falseBC
∴ED∥FG ED=FG,∴四边形DEFG为平行四边形.
12.如图,四边形ABCD中,∠A=90°,AB=3false,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,求EF长度的最大值.
解:连接DN,则EF号DN,当N与B重合时,DN最大,DN=false=6
∴EF的最大值为3.
13.如图所示,在四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并说明理由.
解:连接AC、BD由中位线定理:GH=EF=falseAC,EH=GF=falseBD
∴四边形EFGH为平行四边形
383222540767014.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
解:延长BD交AC于F
∵AD⊥BF,AD平分∠BAF AF=AB=12
∴FC=AC-AF=6,又∵BD=DF BM=MC,
∴DM=falseFC=3.
C 创新拓展提升
15.如图1,△ACB、△AED都是等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连接CE,点M、N分别为BD、CE的中点.
(1)求证:CE=2MN;
(2)将△AED绕A点逆时针旋转一个锐角,如图2,(1)中的结论是否成立?并证明.
图1 图2
(1)证明:延长DN交AC于点F,连接BF,可证△EDN≌△CFN(AAS)
∴DE=FC、DN=FN又∵DM=BM,∴MN是△DBF的中位线,∴BF=2MN
又可证△BCF≌△CAE(SAS)∴BF=EC,∴CE=2MN
(2)解:成立.延长DN至G,使DN=GN,连接BG、CG,延长DE与CA交于点K
∵DN=GN,DM=BM
∴MN是△DBG的中位线,∴BG=2MN,可证△EDN≌△CGN(SAS)DE=CG=AE,∠GCN=∠DEN
∴DE∥CG,∴∠KCG=∠K又可证△CAE≌△BCG(SAS)∴BG=CE,∴CE=2MN.
A 双基导学导练
知识点 三角形的中位线平行于三角形的第三边,且等于第三边的一半
1.如图,在□ABCD中,对角线AC、BD相交于O点,E为CD的中点,若OE=3cm,则AD=( )
A.3cm B.6cm C.9cm D.12cm
第1题图 第2题图 第3题图
2.如图,在△ABC中,D、E分别是边AC、BC的中点,AB=6,则DE= .
3.如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=124°,则
∠ANM= .
4.如图,△ABC中,D、E、F分别为AB、AC、BC的中点.
(1)图中平行四边形有 个;
(2)若AC=5,AB=10,BC=7,则△DEF的周长为 .
5.顺次连接任意四边形四边中点所得到的四边形为 .
6.如图所示,在△ABC中,D、E分别是AB、AC的中点,则BE是△ABC的 ,线段DE是△ABC的
.
第4题图 第6题图
第8题图 第10题图
已知三角形的三条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm.
8.如图,在△MBN中,BM=7,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,□ABCD的周长是 .
9.四边形的两条对角线长分别是14cm和10cm,顺次连接各边中点所得四边形的周长是
10.如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,则PM与PN的大小关系是 .
B真题检测反馈
11.如图,△ABC中,中线BD、CE交于点O,F、G分别为OB、OC的中点,求证:四边形DEFG为平行四边形.
12.如图,四边形ABCD中,∠A=90°,AB=3false,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,求EF长度的最大值.
13.如图所示,在四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并说明理由.
14.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
C 创新拓展提升
15.如图1,△ACB、△AED都是等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连接CE,点M、N分别为BD、CE的中点.
(1)求证:CE=2MN;
(2)将△AED绕A点逆时针旋转一个锐角,如图2,(1)中的结论是否成立?并证明.
图1 图2
18.1平行四边形(第4课时)
A 双基导学导练
知识点 三角形的中位线平行于三角形的第三边,且等于第三边的一半
1.如图,在□ABCD中,对角线AC、BD相交于O点,E为CD的中点,若OE=3cm,则AD=( )
A.3cm B.6cm C.9cm D.12cm
答案:B
第1题图 第2题图 第3题图
2.如图,在△ABC中,D、E分别是边AC、BC的中点,AB=6,则DE= .
答案:3
如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=124°,则
∠ANM= .
答案:56°
4.如图,△ABC中,D、E、F分别为AB、AC、BC的中点.
(1)图中平行四边形有 个;
(2)若AC=5,AB=10,BC=7,则△DEF的周长为 .
答案:3;11
5.顺次连接任意四边形四边中点所得到的四边形为 .
答案:平行四边形
6.如图所示,在△ABC中,D、E分别是AB、AC的中点,则BE是△ABC的 ,线段DE是△ABC的 .
答案:中线,中位线
第4题图 第6题图
第8题图 第10题图
7.已知三角形的三条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm.
答案:26
8.如图,在△MBN中,BM=7,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且
∠NDC=∠MDA,□ABCD的周长是 .
答案:14
9.四边形的两条对角线长分别是14cm和10cm,顺次连接各边中点所得四边形的周长是
答案:24cm
10.如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,则PM与PN的大小关系是 .
答案:PM=PM
B真题检测反馈
11.如图,△ABC中,中线BD、CE交于点O,F、G分别为OB、OC的中点,求证:四边形DEFG为平行四边形.
证明:∵FO=FB, GO=GC,∴FG∥BC且FG=falseBC
∵AE=EB AD=DC,∴ED∥BC且ED=falseBC
∴ED∥FG ED=FG,∴四边形DEFG为平行四边形.
12.如图,四边形ABCD中,∠A=90°,AB=3false,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,求EF长度的最大值.
解:连接DN,则EF号DN,当N与B重合时,DN最大,DN=false=6
∴EF的最大值为3.
13.如图所示,在四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并说明理由.
解:连接AC、BD由中位线定理:GH=EF=falseAC,EH=GF=falseBD
∴四边形EFGH为平行四边形
383222540767014.如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12,AC=18,求MD的长.
解:延长BD交AC于F
∵AD⊥BF,AD平分∠BAF AF=AB=12
∴FC=AC-AF=6,又∵BD=DF BM=MC,
∴DM=falseFC=3.
C 创新拓展提升
15.如图1,△ACB、△AED都是等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连接CE,点M、N分别为BD、CE的中点.
(1)求证:CE=2MN;
(2)将△AED绕A点逆时针旋转一个锐角,如图2,(1)中的结论是否成立?并证明.
图1 图2
(1)证明:延长DN交AC于点F,连接BF,可证△EDN≌△CFN(AAS)
∴DE=FC、DN=FN又∵DM=BM,∴MN是△DBF的中位线,∴BF=2MN
又可证△BCF≌△CAE(SAS)∴BF=EC,∴CE=2MN
(2)解:成立.延长DN至G,使DN=GN,连接BG、CG,延长DE与CA交于点K
∵DN=GN,DM=BM
∴MN是△DBG的中位线,∴BG=2MN,可证△EDN≌△CGN(SAS)DE=CG=AE,∠GCN=∠DEN
∴DE∥CG,∴∠KCG=∠K又可证△CAE≌△BCG(SAS)∴BG=CE,∴CE=2MN.
