2020--2021学年人教版八年级数学下册第十八章《平行四边形》单元练习题(word版含答案) (3)
文档属性
| 名称 | 2020--2021学年人教版八年级数学下册第十八章《平行四边形》单元练习题(word版含答案) (3) |  | |
| 格式 | zip | ||
| 文件大小 | 664.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 16:20:05 | ||
图片预览


文档简介
人教版八年级数学下册第十八章《平行四边形》
单元练习题(含答案)
一、单选题
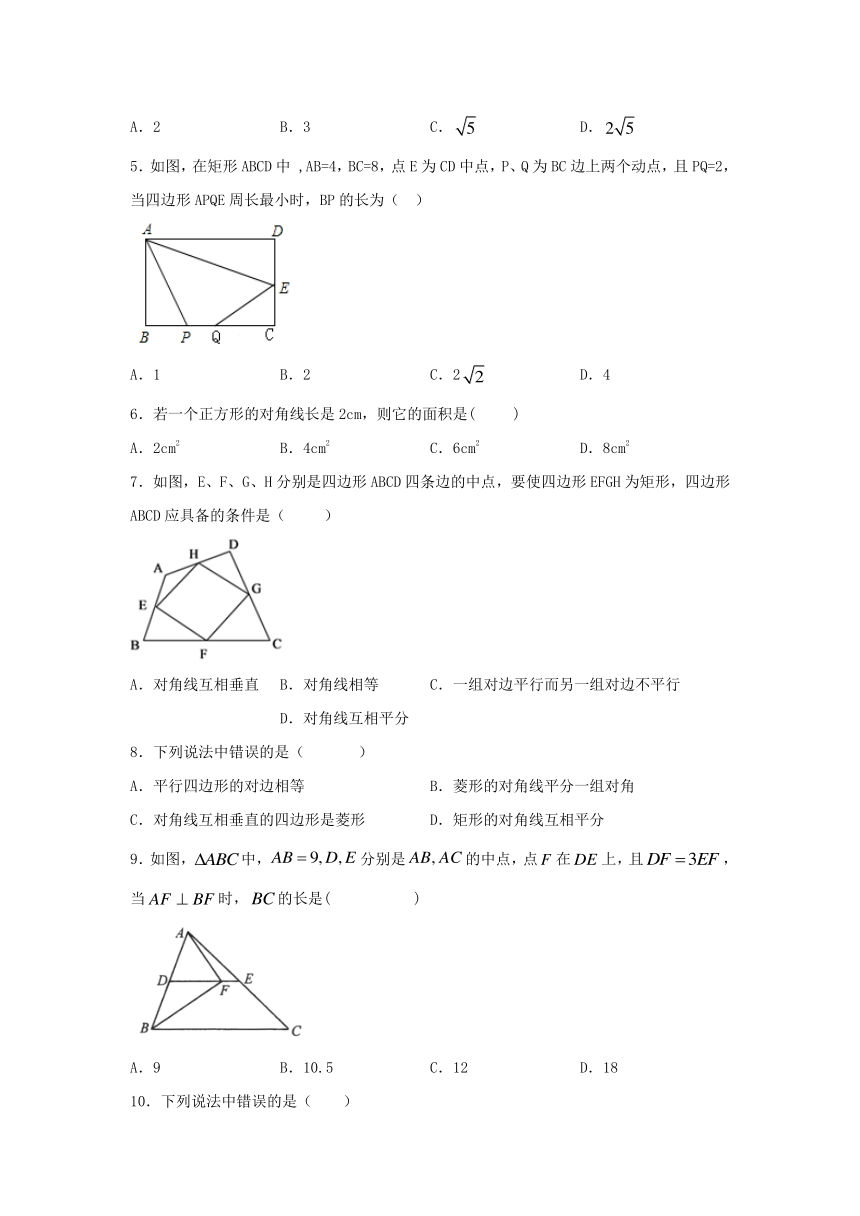
1.如图,在长方形ABCD中,AB=6,BC=8,∠ABC的平分线交AD于点E,连接CE,过B点作BF⊥CE于点F,则BF的长为( )
A.
B.
C.
D.
2.如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为(
)
A.(1,1)
B.
C.
D.
3.如图,在菱形中,对角线AC、BD的长分别为8cm、6cm,则这个菱形的周长为(
)
A.10cm
B.14cm
C.20cm
D.28cm
4.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF∥BE交AC于F,则EF的长等于( )
A.2
B.3
C.
D.
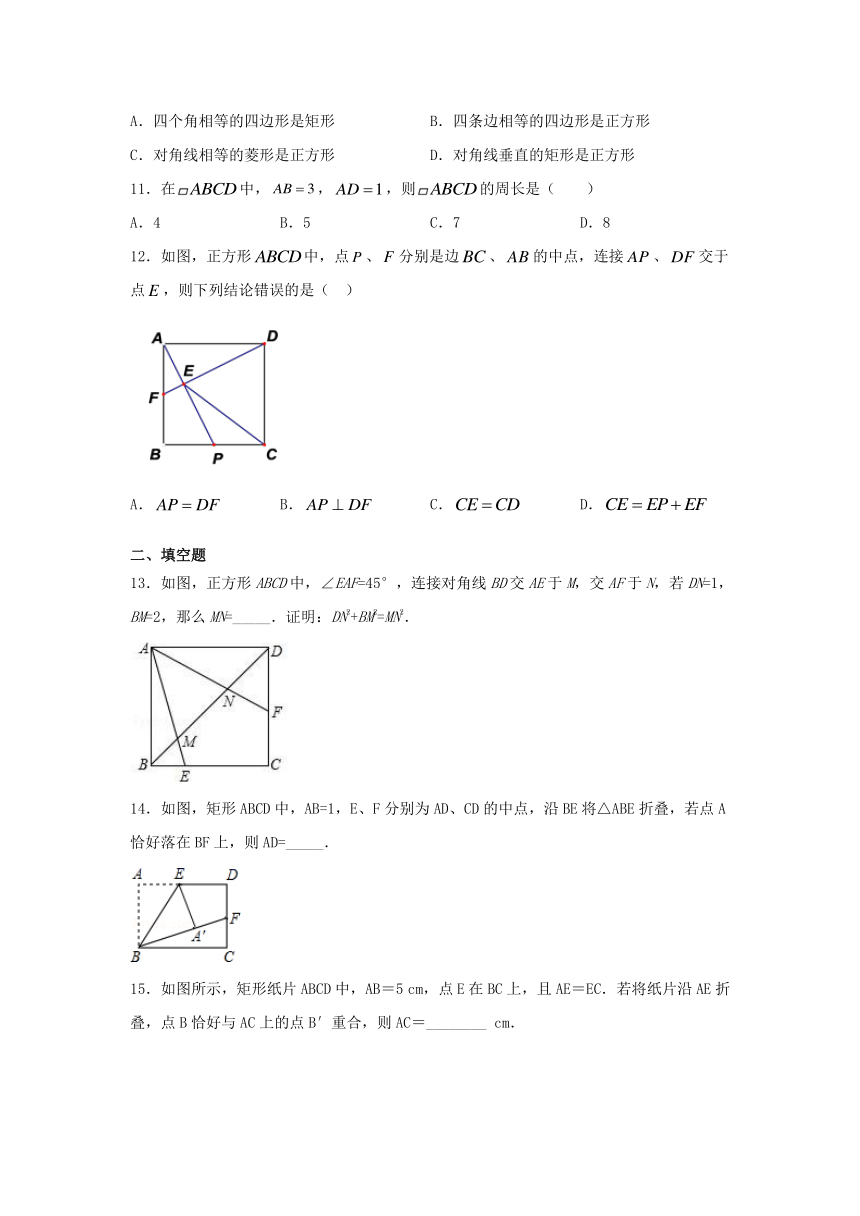
5.如图,在矩形ABCD中
,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为(
)
A.1
B.2
C.2
D.4
6.若一个正方形的对角线长是2cm,则它的面积是(
)
A.2cm2
B.4cm2
C.6cm2
D.8cm2
7.如图,E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是(
)
A.对角线互相垂直
B.对角线相等
C.一组对边平行而另一组对边不平行
D.对角线互相平分
8.下列说法中错误的是(
)
A.平行四边形的对边相等
B.菱形的对角线平分一组对角
C.对角线互相垂直的四边形是菱形
D.矩形的对角线互相平分
9.如图,中,分别是的中点,点在上,且,当时,的长是(
?
???)
A.9
B.10.5
C.12
D.18
10.下列说法中错误的是(
)
A.四个角相等的四边形是矩形
B.四条边相等的四边形是正方形
C.对角线相等的菱形是正方形
D.对角线垂直的矩形是正方形
11.在中,,,则的周长是(
)
A.4
B.5
C.7
D.8
12.如图,正方形中,点、分别是边、的中点,连接、交于点,则下列结论错误的是(
)
A.
B.
C.
D.
二、填空题
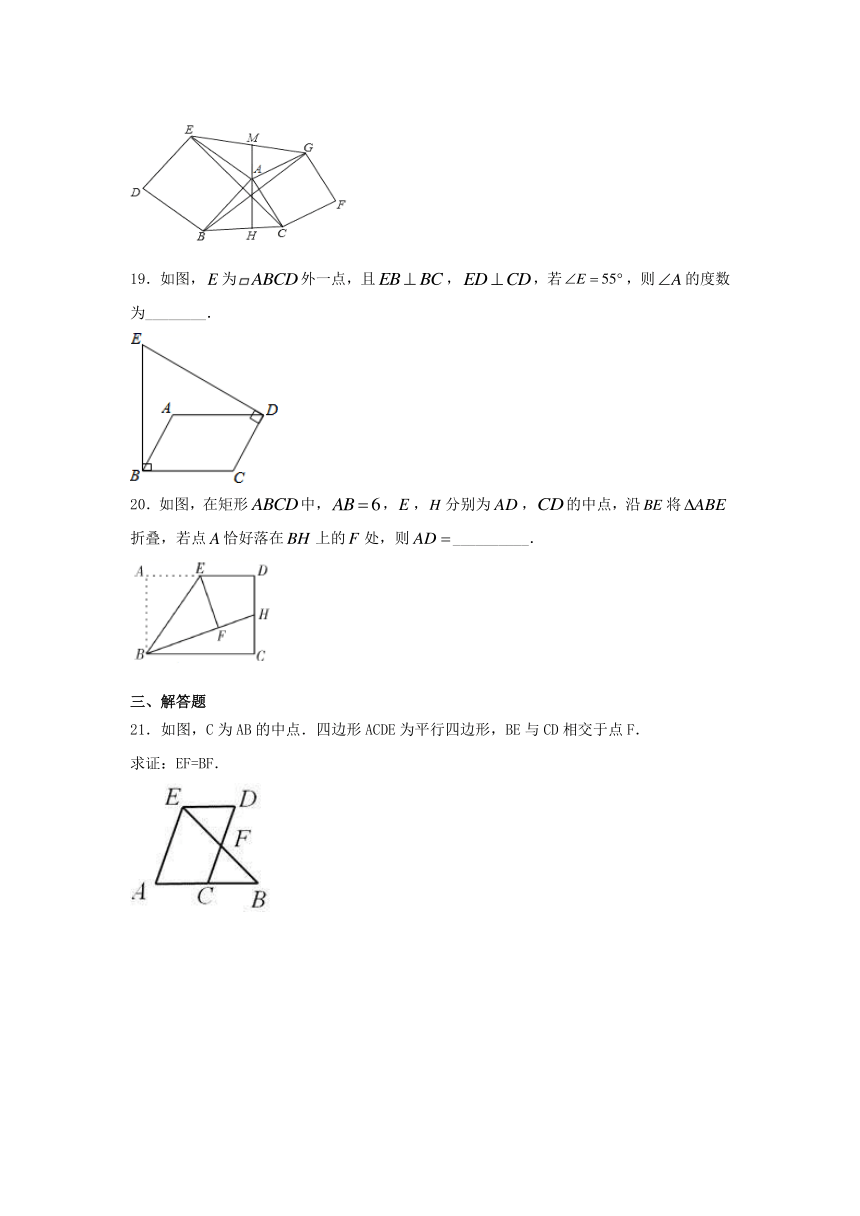
13.如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN=_____.证明:DN2+BM2=MN2.
14.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=_____.
15.如图所示,矩形纸片ABCD中,AB=5
cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=________
cm.
16.如图所示,为矩形的边上一点,动点、同时从点出发,点以秒的速度沿折线运动到点时停止,点以秒的速度沿运动到点时停止.设、同时出发秒时,的面积为.已知与的函数关系图象如图(其中曲线为抛物线的一部分,其余各部分均为线段),则下列结论:①;②当时,;③;④当秒时,;⑤当的面积为时,时间的值是或;?其中正确的结论是________.
17.如图,把菱形ABCD沿AH折叠,B落在BC上的点E处,若∠BAE=40°,则∠EDC的大小为_____.
18.在锐角三角形ABC中,AH是边BC的高,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC.其中正确的是_________.
19.如图,为外一点,且,,若,则的度数为________.
20.如图,在矩形中,,,分别为,的中点,沿将折叠,若点恰好落在上的处,则__________.
三、解答题
21.如图,C为AB的中点.四边形ACDE为平行四边形,BE与CD相交于点F.
求证:EF=BF.
22.如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,AC、EF交于点O.求证:OE=OF.
23.如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm、bcm,满足(a﹣3)2+|2a+b﹣9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D.设运动时间为ts.
(1)a=
cm,b=
cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.
24.如图,平行四边形中,点分别是的中点.求证.
25.如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
26.如图,在中,,点分别是上的中点,连接并延长至点,使,连接.
(1)证明:;
(2)若,AC=2,连接BF,求BF的长.
27.在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.
(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为
°.
(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.
(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.
28.如图,在中,,,、分别在、上,连接、交于点,且.
(1)如图1,求证:.
(2)如图2,是的中点,试探讨与的位置关系.
(3)如图3,、分别是、的中点,若,,求的面积.
29.已知,在直角坐标系中,A(a,0),B(0,b),a?+b?+10a?10b+50=0.
(1)如图1,求A,B的坐标.
(2)如图2,C是OA上一点,OA的垂直平分线交BC于P,且∠POA=15°,求BP的长.
(3)如图3,如A,B以相同速度分别向x轴负方向和y轴正方向移动,D是B关于x轴的对称点,C是OA上一点,过A,D点作BC的垂线,垂足N(n,?3),M(m,t),求m,n之间的数量关系式.
参考答案
1.C2.B3.C4.C5.D6.A7.A8.C9.C10.B11.D12.D
13.
14.
15.10
16.②③④
17.15°
18.①②③④
19.125°
20.
21.证明:∵四边形ACDE为平行四边形,∴ED=AC,ED∥AC.∴∠D=∠FCB,∠DEF=∠B.
又∵C为AB的中点,∴AC=BC.∴ED=BC.
在△DEF和△CBF中,∵∠D=∠FCB,ED=BC,∠DEF=∠B,
∴△DEF≌△CBF(SAS).∴EF=BF.
根据平行四边形对边平行且相等的性质,易用SAS证明△DEF≌△CBF,从而根据全等三角形对应边相等的性质即可证得EF=BF.
22证明:连接AF、EC,如下图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E、F分别是AB、CD的中点,
∴AE=CF,
∵AE∥CF,
∴四边形AECF为平行四边形,
∴OE=OF.
23.(1)3,3;(2)t=2s时,EP把四边形BCDE的周长平分;(3)当t=s或s或5s时,△BPQ的面积等于6cm2.
24.证明:四边形是平行四边形,
,
点分别是的中点,
,
,
在和中,,
.
25.(1)证明:∵AC、CF分别是正方形ABCD和正方形CGFE的对角线,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
又∵H是AF的中点,
∴CH=HF;
(2)∵CH=HF,EC=EF,
∴点H和点E都在线段CF的中垂线上,
∴HE是CF的中垂线,
∴点H和点O是线段AF和CF的中点,
∴OH=AC,
在Rt△ACD和Rt△CEF中,AD=DC=1,CE=EF=3,
∴AC=,
∴CF=3,
又OE是等腰直角△CEF斜边上的高,
∴OE=,
∴HE=HO+OE=2;
26.(1)∵D,E分别是BC,AB上的中点
∴DE为△ABC的中位线
∴DE∥AC,AC=2DE
又∵DF=2DE
∴EF=AC
∴四边形ACEF为平行四边形
∴AF=CE
(2)∵∠ABC=90°,∠B=30°,AC=2
∴
∵D为BC中点
∴
又∵EF=2DE
∴EF=2
∴DF=3
在△BDF中,由勾股定理得
.
27.(1)18;(2)CE的长为;(3)CG的长为.
28.(1)在△ACE和△BCD中,
,
∴△ACE≌△BCD,
∴∠CAE=∠CBD;
(2)如图2,记AE与CF的交点为M,
在Rt△BCD中,点F是BD的中点,
∴CF=BF,
∴∠BCF=∠CBF,
由(1)知,∠CAE=∠CBD,
∴∠BCF=∠CAE,
∴∠CAE+∠ACF=∠BCF+∠ACF=∠ACB=90°,
∴∠AMC=90°,
∴AE⊥CF;
(3)如图3,记AE与CF的交点为M,
∵AC=2
,
∴BC=AC=2,
∵CE=1,
∴CD=CE=1,
在Rt△BCD中,根据勾股定理得,BD==3,
∵点F是BD中点,
∴CF=DF=
,
同理:EG=,
连接EF,过点F作FH⊥BC,
∵∠ACB=90°,点F是BD的中点,
∴FH=,
∴S△CEF=CE?FH=×1×=,
由(2)知,AE⊥CF,
∴S△CEF=CF?ME=×ME=ME,
∴ME=,
∴ME=,
∴GM=EG-ME=,
∴S△CFG=CF?GM=××.
29.(1)A(-5,0),B(0,5);(2)5,(3)n-m=3
单元练习题(含答案)
一、单选题
1.如图,在长方形ABCD中,AB=6,BC=8,∠ABC的平分线交AD于点E,连接CE,过B点作BF⊥CE于点F,则BF的长为( )
A.
B.
C.
D.
2.如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为(
)
A.(1,1)
B.
C.
D.
3.如图,在菱形中,对角线AC、BD的长分别为8cm、6cm,则这个菱形的周长为(
)
A.10cm
B.14cm
C.20cm
D.28cm
4.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF∥BE交AC于F,则EF的长等于( )
A.2
B.3
C.
D.
5.如图,在矩形ABCD中
,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为(
)
A.1
B.2
C.2
D.4
6.若一个正方形的对角线长是2cm,则它的面积是(
)
A.2cm2
B.4cm2
C.6cm2
D.8cm2
7.如图,E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是(
)
A.对角线互相垂直
B.对角线相等
C.一组对边平行而另一组对边不平行
D.对角线互相平分
8.下列说法中错误的是(
)
A.平行四边形的对边相等
B.菱形的对角线平分一组对角
C.对角线互相垂直的四边形是菱形
D.矩形的对角线互相平分
9.如图,中,分别是的中点,点在上,且,当时,的长是(
?
???)
A.9
B.10.5
C.12
D.18
10.下列说法中错误的是(
)
A.四个角相等的四边形是矩形
B.四条边相等的四边形是正方形
C.对角线相等的菱形是正方形
D.对角线垂直的矩形是正方形
11.在中,,,则的周长是(
)
A.4
B.5
C.7
D.8
12.如图,正方形中,点、分别是边、的中点,连接、交于点,则下列结论错误的是(
)
A.
B.
C.
D.
二、填空题
13.如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN=_____.证明:DN2+BM2=MN2.
14.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=_____.
15.如图所示,矩形纸片ABCD中,AB=5
cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=________
cm.
16.如图所示,为矩形的边上一点,动点、同时从点出发,点以秒的速度沿折线运动到点时停止,点以秒的速度沿运动到点时停止.设、同时出发秒时,的面积为.已知与的函数关系图象如图(其中曲线为抛物线的一部分,其余各部分均为线段),则下列结论:①;②当时,;③;④当秒时,;⑤当的面积为时,时间的值是或;?其中正确的结论是________.
17.如图,把菱形ABCD沿AH折叠,B落在BC上的点E处,若∠BAE=40°,则∠EDC的大小为_____.
18.在锐角三角形ABC中,AH是边BC的高,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC.其中正确的是_________.
19.如图,为外一点,且,,若,则的度数为________.
20.如图,在矩形中,,,分别为,的中点,沿将折叠,若点恰好落在上的处,则__________.
三、解答题
21.如图,C为AB的中点.四边形ACDE为平行四边形,BE与CD相交于点F.
求证:EF=BF.
22.如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,AC、EF交于点O.求证:OE=OF.
23.如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm、bcm,满足(a﹣3)2+|2a+b﹣9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D.设运动时间为ts.
(1)a=
cm,b=
cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.
24.如图,平行四边形中,点分别是的中点.求证.
25.如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
26.如图,在中,,点分别是上的中点,连接并延长至点,使,连接.
(1)证明:;
(2)若,AC=2,连接BF,求BF的长.
27.在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.
(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为
°.
(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.
(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.
28.如图,在中,,,、分别在、上,连接、交于点,且.
(1)如图1,求证:.
(2)如图2,是的中点,试探讨与的位置关系.
(3)如图3,、分别是、的中点,若,,求的面积.
29.已知,在直角坐标系中,A(a,0),B(0,b),a?+b?+10a?10b+50=0.
(1)如图1,求A,B的坐标.
(2)如图2,C是OA上一点,OA的垂直平分线交BC于P,且∠POA=15°,求BP的长.
(3)如图3,如A,B以相同速度分别向x轴负方向和y轴正方向移动,D是B关于x轴的对称点,C是OA上一点,过A,D点作BC的垂线,垂足N(n,?3),M(m,t),求m,n之间的数量关系式.
参考答案
1.C2.B3.C4.C5.D6.A7.A8.C9.C10.B11.D12.D
13.
14.
15.10
16.②③④
17.15°
18.①②③④
19.125°
20.
21.证明:∵四边形ACDE为平行四边形,∴ED=AC,ED∥AC.∴∠D=∠FCB,∠DEF=∠B.
又∵C为AB的中点,∴AC=BC.∴ED=BC.
在△DEF和△CBF中,∵∠D=∠FCB,ED=BC,∠DEF=∠B,
∴△DEF≌△CBF(SAS).∴EF=BF.
根据平行四边形对边平行且相等的性质,易用SAS证明△DEF≌△CBF,从而根据全等三角形对应边相等的性质即可证得EF=BF.
22证明:连接AF、EC,如下图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E、F分别是AB、CD的中点,
∴AE=CF,
∵AE∥CF,
∴四边形AECF为平行四边形,
∴OE=OF.
23.(1)3,3;(2)t=2s时,EP把四边形BCDE的周长平分;(3)当t=s或s或5s时,△BPQ的面积等于6cm2.
24.证明:四边形是平行四边形,
,
点分别是的中点,
,
,
在和中,,
.
25.(1)证明:∵AC、CF分别是正方形ABCD和正方形CGFE的对角线,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
又∵H是AF的中点,
∴CH=HF;
(2)∵CH=HF,EC=EF,
∴点H和点E都在线段CF的中垂线上,
∴HE是CF的中垂线,
∴点H和点O是线段AF和CF的中点,
∴OH=AC,
在Rt△ACD和Rt△CEF中,AD=DC=1,CE=EF=3,
∴AC=,
∴CF=3,
又OE是等腰直角△CEF斜边上的高,
∴OE=,
∴HE=HO+OE=2;
26.(1)∵D,E分别是BC,AB上的中点
∴DE为△ABC的中位线
∴DE∥AC,AC=2DE
又∵DF=2DE
∴EF=AC
∴四边形ACEF为平行四边形
∴AF=CE
(2)∵∠ABC=90°,∠B=30°,AC=2
∴
∵D为BC中点
∴
又∵EF=2DE
∴EF=2
∴DF=3
在△BDF中,由勾股定理得
.
27.(1)18;(2)CE的长为;(3)CG的长为.
28.(1)在△ACE和△BCD中,
,
∴△ACE≌△BCD,
∴∠CAE=∠CBD;
(2)如图2,记AE与CF的交点为M,
在Rt△BCD中,点F是BD的中点,
∴CF=BF,
∴∠BCF=∠CBF,
由(1)知,∠CAE=∠CBD,
∴∠BCF=∠CAE,
∴∠CAE+∠ACF=∠BCF+∠ACF=∠ACB=90°,
∴∠AMC=90°,
∴AE⊥CF;
(3)如图3,记AE与CF的交点为M,
∵AC=2
,
∴BC=AC=2,
∵CE=1,
∴CD=CE=1,
在Rt△BCD中,根据勾股定理得,BD==3,
∵点F是BD中点,
∴CF=DF=
,
同理:EG=,
连接EF,过点F作FH⊥BC,
∵∠ACB=90°,点F是BD的中点,
∴FH=,
∴S△CEF=CE?FH=×1×=,
由(2)知,AE⊥CF,
∴S△CEF=CF?ME=×ME=ME,
∴ME=,
∴ME=,
∴GM=EG-ME=,
∴S△CFG=CF?GM=××.
29.(1)A(-5,0),B(0,5);(2)5,(3)n-m=3
