2020-2021学年人教版八年级下册数学第18章 平行四边形 单元试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章 平行四边形 单元试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 286.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 11:36:16 | ||
图片预览




文档简介
第18章
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
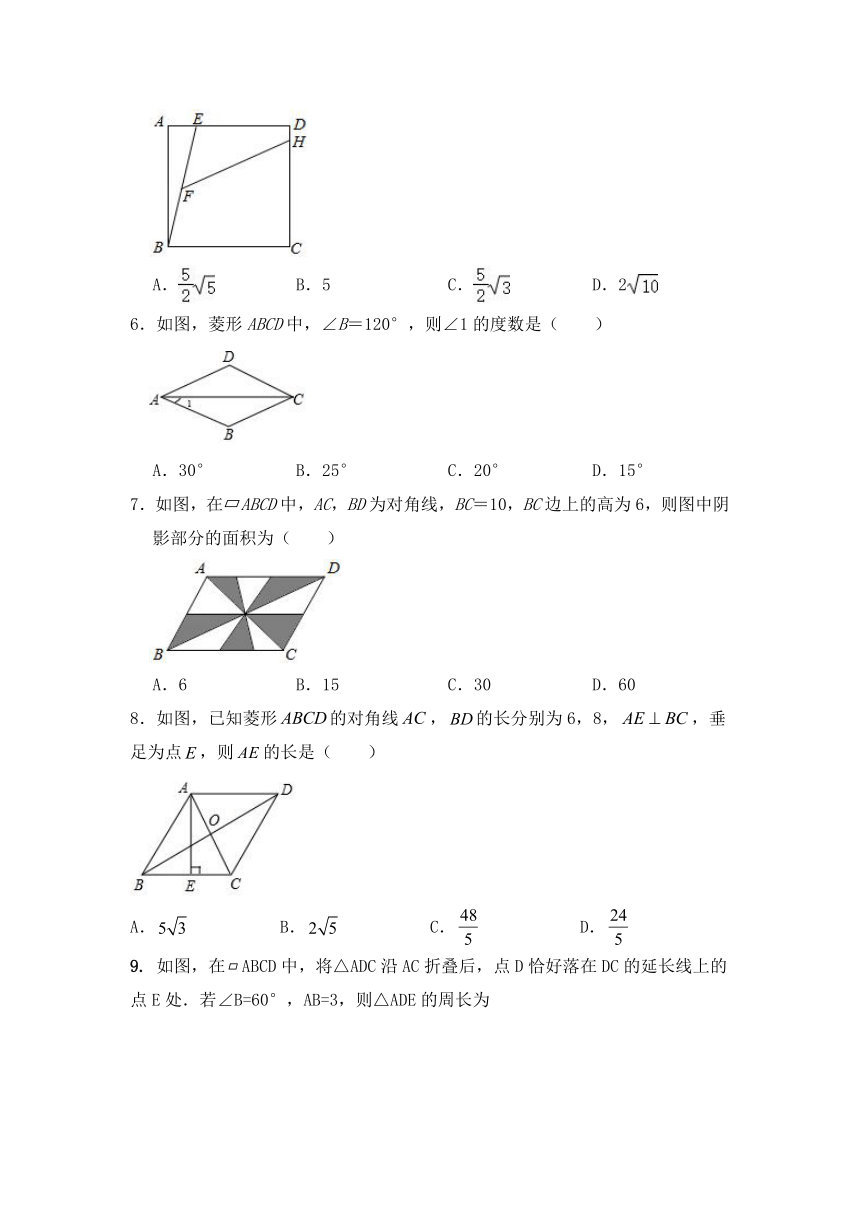
1.在菱形ABCD中,,E、F分别是边AB和BC的中点,,垂足为P,则
A.
B.
C.
D.
(第1题图)
(第2题图)
2.如图,四边形ABCD是长方形,把沿AC翻折到,与BC交于点E,若,,则BE的长是
A.
B.
C.
D.
1
3.如图,四边形ABCD是菱形,,,于H,则
A.
B.
C.
12
D.
24
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
9.
如图,在ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
A.12
B.15
C.18
D.21
10.
关于?ABCD的叙述,正确的是( )
A.
若AB⊥BC,则?ABCD是菱形
B.
若AC⊥BD,则?ABCD是正方形
C.
若AC=BD,则?ABCD是矩形
D.
若AB=AD,则?ABCD是正方形
二.填空题(每题4分,共20分)
11.对角线
的矩形是正方形.
12.用刻度尺检查一个四边形零件是矩形,你的方法是
,依据是
.
13.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为__________。
14.如图所示,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是__________。
15.在ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是__________。
三.解答题(每题10分,共50分)
16.
如图,在?ABCD中,
(1)若点E、F是AD、BC的中点,连接BE、DF,求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.
17.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:DE=CE.
(2)当EA⊥AB于点A,AE=ED=1时,求菱形的边长.
18.如图,在中,于E,于F,若与的长度之比为3:4,求的值.
19.如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.
20.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.
21.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)将△ABC沿水平方向向左平移3个单位得△A1B1C1,请画出△A1B1C1.
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标.
(3)△A1B1C1与△A2B2C2是否成中心对称,若是请写出对称中心的坐标
,若不是请说明理由.
22.(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF=
.若AB=4,则△CEF的周长为
.
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
参考答案
一.选择题
1.A
2.C
3.
B.
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
C.
10.C
二.填空题(共5小题)
11.
互相垂直
12.
先测量两组对边是否相等,然后测量两条对角线是否相等;对角线相等的平行四边形是矩形.
13.24
14.22.5°
15.①②③
三.解答题(共5小题)
16.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是?ABCD边AD、BC的中点,
∴DE=AD,BF=BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.
17.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
又∵AE=DE,
∴DE=CE.
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
即菱形的边长为.
18.3:4
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20.(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(SAS),
∴∠AFD=∠AFB,
∵∠AFB=∠CFE,
∴∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD+∠CBE=∠CDF+∠EFD,
∴∠EFD=∠BCD.
【点评】此题主要考查了全等三角形的判定与性质,以及菱形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
21.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2(﹣1,﹣4),B2(﹣4,﹣2),C2(﹣3,﹣5);
(3)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为:(﹣1.5,0).
故答案为:(﹣1.5,0).
22.解:(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,
即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.在菱形ABCD中,,E、F分别是边AB和BC的中点,,垂足为P,则
A.
B.
C.
D.
(第1题图)
(第2题图)
2.如图,四边形ABCD是长方形,把沿AC翻折到,与BC交于点E,若,,则BE的长是
A.
B.
C.
D.
1
3.如图,四边形ABCD是菱形,,,于H,则
A.
B.
C.
12
D.
24
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
9.
如图,在ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
A.12
B.15
C.18
D.21
10.
关于?ABCD的叙述,正确的是( )
A.
若AB⊥BC,则?ABCD是菱形
B.
若AC⊥BD,则?ABCD是正方形
C.
若AC=BD,则?ABCD是矩形
D.
若AB=AD,则?ABCD是正方形
二.填空题(每题4分,共20分)
11.对角线
的矩形是正方形.
12.用刻度尺检查一个四边形零件是矩形,你的方法是
,依据是
.
13.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为__________。
14.如图所示,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是__________。
15.在ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是__________。
三.解答题(每题10分,共50分)
16.
如图,在?ABCD中,
(1)若点E、F是AD、BC的中点,连接BE、DF,求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.
17.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:DE=CE.
(2)当EA⊥AB于点A,AE=ED=1时,求菱形的边长.
18.如图,在中,于E,于F,若与的长度之比为3:4,求的值.
19.如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.
20.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.
21.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)将△ABC沿水平方向向左平移3个单位得△A1B1C1,请画出△A1B1C1.
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标.
(3)△A1B1C1与△A2B2C2是否成中心对称,若是请写出对称中心的坐标
,若不是请说明理由.
22.(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF=
.若AB=4,则△CEF的周长为
.
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
参考答案
一.选择题
1.A
2.C
3.
B.
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
C.
10.C
二.填空题(共5小题)
11.
互相垂直
12.
先测量两组对边是否相等,然后测量两条对角线是否相等;对角线相等的平行四边形是矩形.
13.24
14.22.5°
15.①②③
三.解答题(共5小题)
16.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是?ABCD边AD、BC的中点,
∴DE=AD,BF=BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.
17.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
又∵AE=DE,
∴DE=CE.
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
即菱形的边长为.
18.3:4
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20.(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(SAS),
∴∠AFD=∠AFB,
∵∠AFB=∠CFE,
∴∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD+∠CBE=∠CDF+∠EFD,
∴∠EFD=∠BCD.
【点评】此题主要考查了全等三角形的判定与性质,以及菱形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
21.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,A2(﹣1,﹣4),B2(﹣4,﹣2),C2(﹣3,﹣5);
(3)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为:(﹣1.5,0).
故答案为:(﹣1.5,0).
22.解:(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,
即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
