2020—2021学年人教版数学八年级下册 19.2. 2一次函数课件(共23张PPT)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册 19.2. 2一次函数课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 851.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 23:02:55 | ||
图片预览





文档简介
(共23张PPT)
19.2.2
一次函数
2.如图,已知A(1,1)和点B(1,2),可认为
点B是由点A向上平移
个单位得到。
3.如果将点A(1,1)向下平移
2个单位得到点C
,则的点C
的坐标为
1
(1,-1)
复习回顾
1.已知点A(x,y),若A在横轴上,则
=0,
若点A在纵轴上,则
=0
x
y
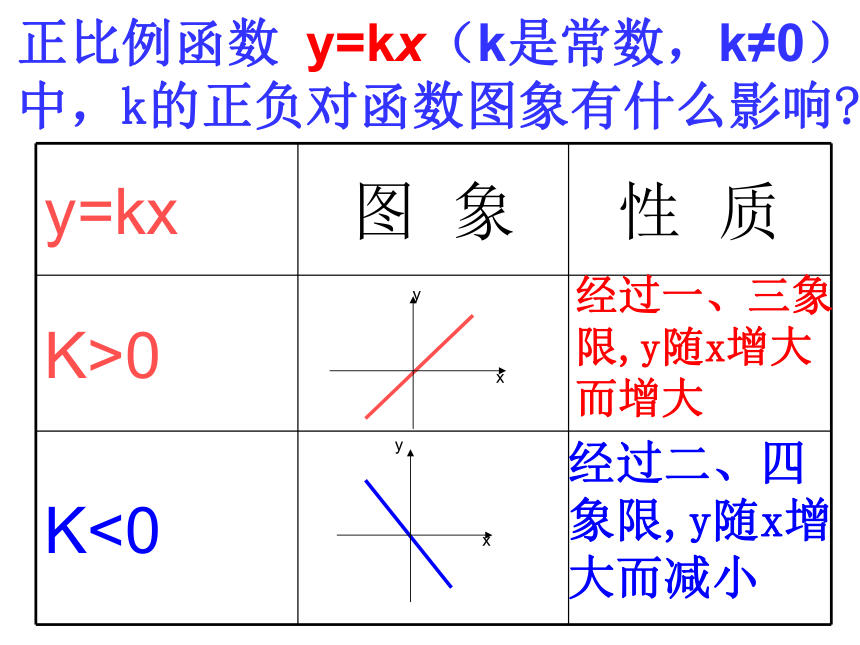
y=kx(k是常数,k≠0)
一条经过原点(0,0)和(1,k)
的直线
正比例函数
y=kx
(k>0)
x
y
y=kx(k<0)
解析式:
图象:
y=kx
图
象
性
质
K>0
K<0
经过一、三象限,y随x增大而增大
经过二、四象限,y随x增大而减小
正比例函数
y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响?
y
x
y
x
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
一次函数的定义:
知识回顾
正比例函数y=kx
(k≠0)是一次函数吗?
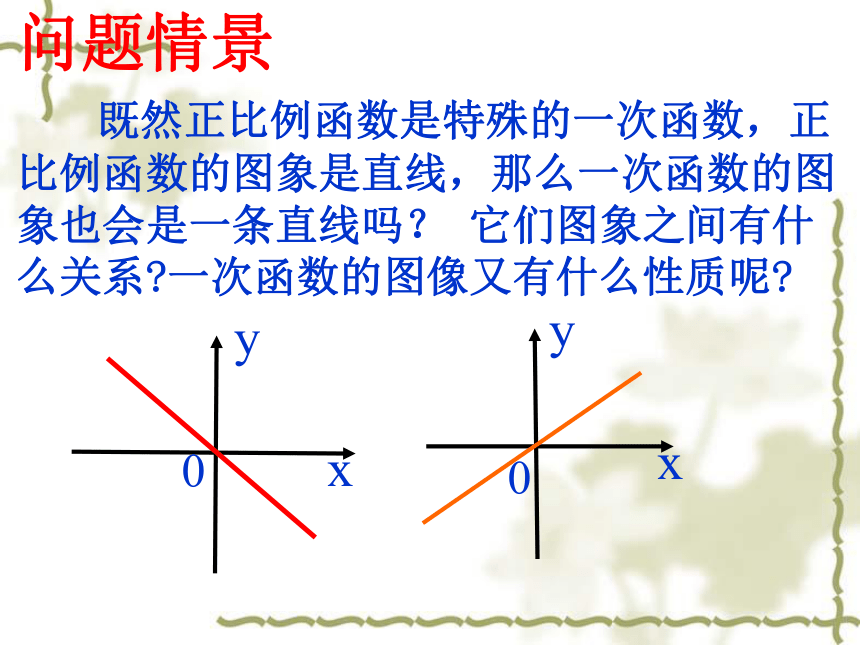
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?
它们图象之间有什么关系?一次函数的图像又有什么性质呢?
x
y
0
x
0
y
问题情景
探究一
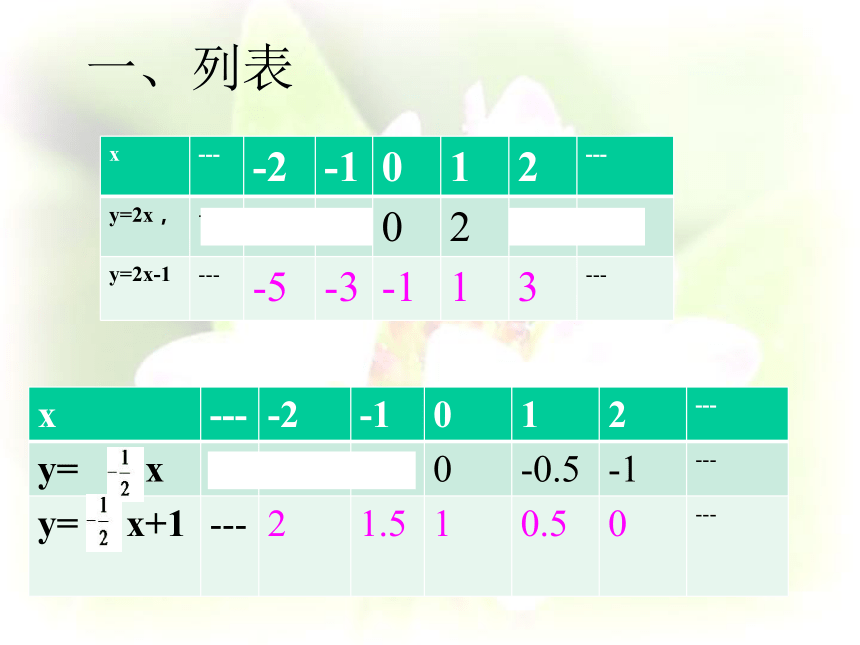
1、在同一坐标系中
用描点法画出函数图象(分组完成)
(1)y=2x,y=2x-1
(
2
)
y=
x,y=
x+1
一、列表
x
---
-2
-1
0
1
2
---
y=2x,
---
-4
-2
0
2
4
---
y=2x-1
---
-5
-3
-1
1
3
---
x
---
-2
-1
0
1
2
---
y=
x
---
1
0.5
0
-0.5
-1
---
y=
x+1
---
2
1.5
1
0.5
0
---
O
x
y
1
2
-1
-2
-1
-2
1
2
3
.
.
y=2x-1
y=2x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
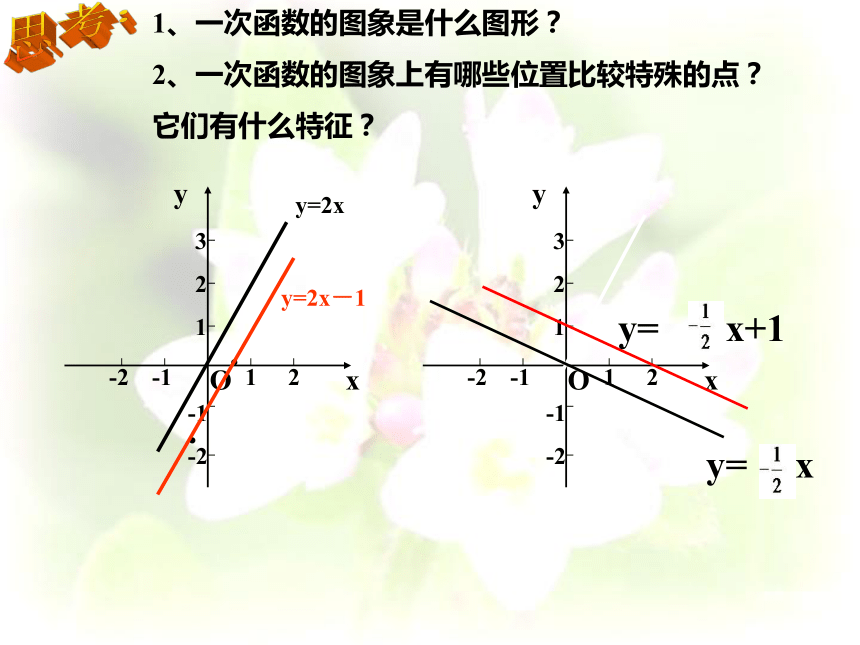
1、一次函数的图象是什么图形?
2、一次函数的图象上有哪些位置比较特殊的点?
它们有什么特征?
思考:
y=
x+1
y=
x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
.
.
y=2x-1
y=2x+3
y=2x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
y=-x
y=-x+3
y=-x-2
3、每组图中的三条直线有什么位置关系?交换两组中的任一条直线后三条直线还平行吗?由此你发现了什么?
思考:
归纳
直线
y
=
kx
+
b与
直线y
=
kx的位置关系
是
__________.
互相平行
直线y
=
kx
+
b是由
直线y
=
kx向___________
平移______个单位长度
得来的.
上或下
︱b
︳
x
y
o
(0,b)
(0,b)
1.直线y=5x-7与直线y=kx+2平行,则k=_______.
2.直线y=3x向上平移2个单位长度得到的直线解析式为________;
直线y=3x+2向下平移4个单位长度得到的直线解析式为________.
5
y=3x+2
y=3x-2
与k有关
与b有关
小试身手
x
y
o
y=2x+3
y=2x
一次函数y=kx+b(k≠0)的性质:
当______时,图象从左
到右逐渐______,y随x的
增大而______.
y=2x-1
当______时,图象从左
到右逐渐______,y随x的
增大而______.
x
y
o
y=-x+3
y=-x
y=-x-2
k>0
k<0
上升
下降
增大
减小
与k有关
与k有关
一次函数图象和性质
y=kx+b
图
象
性
质
直线经过的象限
增减性
K>0
b=0
y
o
x
b>0
y
o
x
b<0
y
o
x
第一、三象限
y随x增大
而增大
第一、三、二象限
y随x增大
而增大
第一、三、四象限
y随x的增大
而增大
(0,
b)
(0,
b)
先由k决定过一三象限,
再由b决定过二或四象限
由k决定
y=kx+b
图
象
性
质
直线经过的象限
增减性
K<0
b=0
y
x
o
b>0
y
x
o
b<0
y
o
x
第二、四象限
y随x增大
而减小
第二、四、一象限
y随x增大
而减小
第二、四、三象限
y随x增大
而减小
(0,
b)
(o,
b)
先由k决定过二四象限,
再由b决定过一或三象限
由k决定
1.函数y=10x-9的图象经过第_________象限,y
的值随着x值的增大而________.
2.函数y=-0.3x+4的图象经过第____________
象限,y的值随着x值的增大而
__________.
增大
减小
一三四
一二四
大显身手
(1)下列函数中,y的值随x值的增大而增大的函数是
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
(2)直线y=3x-2可由直线y=3x向
平移
个单位得到。
尝试舞台
课堂检测:
(C)
下
2
(3)函数y=2x
-
4与y轴的交点(
)与x轴交于
0,-4
(
2,
0
)
课堂小结
1、说说这节课你积累了哪些知识?
2、说说这节课你学到了哪些数学方法?
课外作业:
1、
函数y=3x-4经过
象限,y随x的增大而___。
2、直线y=x+2可由直线y=x-1向
平移
单位得到。
一、填空
3、函数y=2x
-
4与y轴的交点为_____,与x轴交于点______。
4.已知一次函数y=(1-2m)x+m-3
的图像与y轴的交点位于y轴负半轴上,且函数值
y随自变量x的增大而减小,求m的取值范围;
解
:∵一次函数y=(1-2m)x+m-3的图像与y轴的交点位于y轴负半轴上,且函数值y随自变量x的增大而减小
∴
m-3<0
1-2m<0
∴
<m<3
{
根据函数图象确定k,b的取值范围
y
x
o
K>o,
b=o
y
x
o
K>0,
by
x
o
K>o,
b>0
y
x
o
K<0,
b=0
y
x
0
K<0,
b<0
y
x
o
K<0,
b>0
小试牛刀
y
x
0
(D)
y
x
0
(A
)
y
x
0
(C)
y
x
0
(B)
已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
选做题:已知一次函数
y=(1-2m)x+m-1
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;
(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
19.2.2
一次函数
2.如图,已知A(1,1)和点B(1,2),可认为
点B是由点A向上平移
个单位得到。
3.如果将点A(1,1)向下平移
2个单位得到点C
,则的点C
的坐标为
1
(1,-1)
复习回顾
1.已知点A(x,y),若A在横轴上,则
=0,
若点A在纵轴上,则
=0
x
y
y=kx(k是常数,k≠0)
一条经过原点(0,0)和(1,k)
的直线
正比例函数
y=kx
(k>0)
x
y
y=kx(k<0)
解析式:
图象:
y=kx
图
象
性
质
K>0
K<0
经过一、三象限,y随x增大而增大
经过二、四象限,y随x增大而减小
正比例函数
y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响?
y
x
y
x
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
一次函数的定义:
知识回顾
正比例函数y=kx
(k≠0)是一次函数吗?
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?
它们图象之间有什么关系?一次函数的图像又有什么性质呢?
x
y
0
x
0
y
问题情景
探究一
1、在同一坐标系中
用描点法画出函数图象(分组完成)
(1)y=2x,y=2x-1
(
2
)
y=
x,y=
x+1
一、列表
x
---
-2
-1
0
1
2
---
y=2x,
---
-4
-2
0
2
4
---
y=2x-1
---
-5
-3
-1
1
3
---
x
---
-2
-1
0
1
2
---
y=
x
---
1
0.5
0
-0.5
-1
---
y=
x+1
---
2
1.5
1
0.5
0
---
O
x
y
1
2
-1
-2
-1
-2
1
2
3
.
.
y=2x-1
y=2x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
1、一次函数的图象是什么图形?
2、一次函数的图象上有哪些位置比较特殊的点?
它们有什么特征?
思考:
y=
x+1
y=
x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
.
.
y=2x-1
y=2x+3
y=2x
O
x
y
1
2
-1
-2
-1
-2
1
2
3
y=-x
y=-x+3
y=-x-2
3、每组图中的三条直线有什么位置关系?交换两组中的任一条直线后三条直线还平行吗?由此你发现了什么?
思考:
归纳
直线
y
=
kx
+
b与
直线y
=
kx的位置关系
是
__________.
互相平行
直线y
=
kx
+
b是由
直线y
=
kx向___________
平移______个单位长度
得来的.
上或下
︱b
︳
x
y
o
(0,b)
(0,b)
1.直线y=5x-7与直线y=kx+2平行,则k=_______.
2.直线y=3x向上平移2个单位长度得到的直线解析式为________;
直线y=3x+2向下平移4个单位长度得到的直线解析式为________.
5
y=3x+2
y=3x-2
与k有关
与b有关
小试身手
x
y
o
y=2x+3
y=2x
一次函数y=kx+b(k≠0)的性质:
当______时,图象从左
到右逐渐______,y随x的
增大而______.
y=2x-1
当______时,图象从左
到右逐渐______,y随x的
增大而______.
x
y
o
y=-x+3
y=-x
y=-x-2
k>0
k<0
上升
下降
增大
减小
与k有关
与k有关
一次函数图象和性质
y=kx+b
图
象
性
质
直线经过的象限
增减性
K>0
b=0
y
o
x
b>0
y
o
x
b<0
y
o
x
第一、三象限
y随x增大
而增大
第一、三、二象限
y随x增大
而增大
第一、三、四象限
y随x的增大
而增大
(0,
b)
(0,
b)
先由k决定过一三象限,
再由b决定过二或四象限
由k决定
y=kx+b
图
象
性
质
直线经过的象限
增减性
K<0
b=0
y
x
o
b>0
y
x
o
b<0
y
o
x
第二、四象限
y随x增大
而减小
第二、四、一象限
y随x增大
而减小
第二、四、三象限
y随x增大
而减小
(0,
b)
(o,
b)
先由k决定过二四象限,
再由b决定过一或三象限
由k决定
1.函数y=10x-9的图象经过第_________象限,y
的值随着x值的增大而________.
2.函数y=-0.3x+4的图象经过第____________
象限,y的值随着x值的增大而
__________.
增大
减小
一三四
一二四
大显身手
(1)下列函数中,y的值随x值的增大而增大的函数是
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
(2)直线y=3x-2可由直线y=3x向
平移
个单位得到。
尝试舞台
课堂检测:
(C)
下
2
(3)函数y=2x
-
4与y轴的交点(
)与x轴交于
0,-4
(
2,
0
)
课堂小结
1、说说这节课你积累了哪些知识?
2、说说这节课你学到了哪些数学方法?
课外作业:
1、
函数y=3x-4经过
象限,y随x的增大而___。
2、直线y=x+2可由直线y=x-1向
平移
单位得到。
一、填空
3、函数y=2x
-
4与y轴的交点为_____,与x轴交于点______。
4.已知一次函数y=(1-2m)x+m-3
的图像与y轴的交点位于y轴负半轴上,且函数值
y随自变量x的增大而减小,求m的取值范围;
解
:∵一次函数y=(1-2m)x+m-3的图像与y轴的交点位于y轴负半轴上,且函数值y随自变量x的增大而减小
∴
m-3<0
1-2m<0
∴
<m<3
{
根据函数图象确定k,b的取值范围
y
x
o
K>o,
b=o
y
x
o
K>0,
b
x
o
K>o,
b>0
y
x
o
K<0,
b=0
y
x
0
K<0,
b<0
y
x
o
K<0,
b>0
小试牛刀
y
x
0
(D)
y
x
0
(A
)
y
x
0
(C)
y
x
0
(B)
已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
选做题:已知一次函数
y=(1-2m)x+m-1
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;
(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
