2020-2021学年北师大版八年级数学下册3.1图形的平移-同步提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.1图形的平移-同步提升训练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 11:57:32 | ||
图片预览

文档简介
2020-2021年度北师大版八年级数学下册《3.1图形的平移》同步提升训练(附答案)
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2)
B.(﹣3,﹣1)
C.(﹣3,4)
D.(﹣1,2)
2.如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )
A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5
3.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3( )
A.70°
B.180°
C.110°
D.80°
4.线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7)
B.(4,3)
C.(﹣5,10)
D.(﹣3,7)
5.下列现象中,属于平移的是( )
①小朋友在荡秋千;②打气筒打气时,活塞的运动;
③钟摆的摆动;④瓶装饮料在传送带上移动.
A.①②
B.①③
C.②③
D.②④
6.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
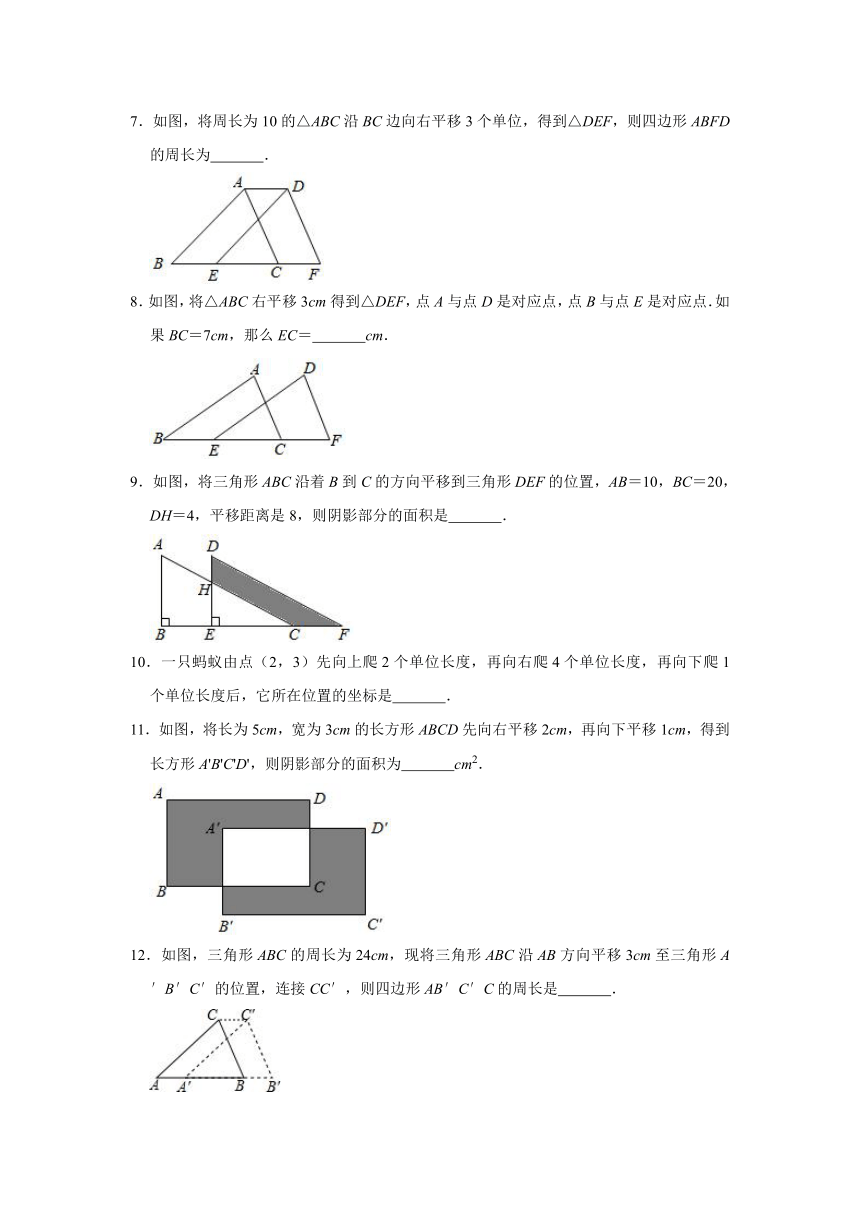
7.如图,将周长为10的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为
.
8.如图,将△ABC右平移3cm得到△DEF,点A与点D是对应点,点B与点E是对应点.如果BC=7cm,那么EC=
cm.
9.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,平移距离是8,则阴影部分的面积是
.
10.一只蚂蚁由点(2,3)先向上爬2个单位长度,再向右爬4个单位长度,再向下爬1个单位长度后,它所在位置的坐标是
.
11.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为
cm2.
12.如图,三角形ABC的周长为24cm,现将三角形ABC沿AB方向平移3cm至三角形A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是
.
13.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为
.
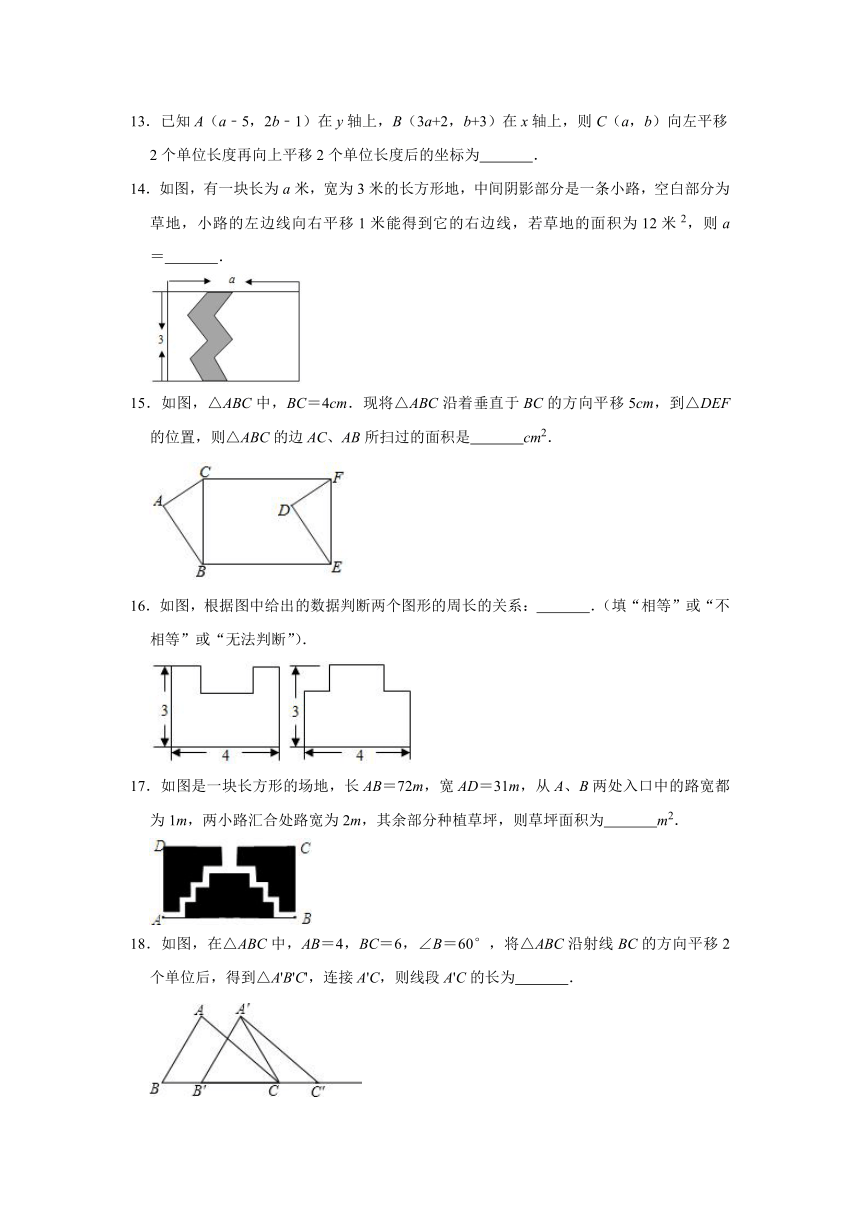
14.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a=
.
15.如图,△ABC中,BC=4cm.现将△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,则△ABC的边AC、AB所扫过的面积是
cm2.
16.如图,根据图中给出的数据判断两个图形的周长的关系:
.(填“相等”或“不相等”或“无法判断”).
17.如图是一块长方形的场地,长AB=72m,宽AD=31m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为
m2.
18.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为
.
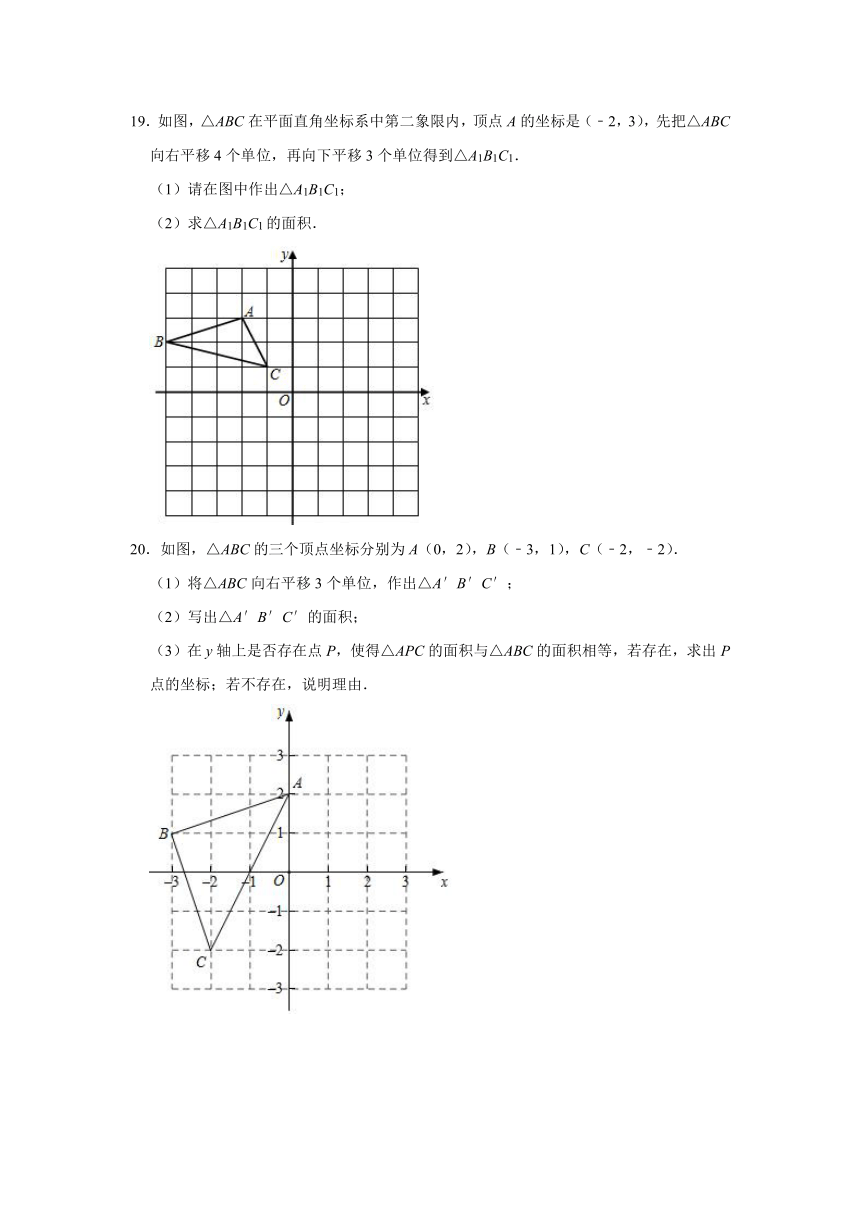
19.如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位,再向下平移3个单位得到△A1B1C1.
(1)请在图中作出△A1B1C1;
(2)求△A1B1C1的面积.
20.如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).
(1)将△ABC向右平移3个单位,作出△A′B′C′;
(2)写出△A′B′C′的面积;
(3)在y轴上是否存在点P,使得△APC的面积与△ABC的面积相等,若存在,求出P点的坐标;若不存在,说明理由.
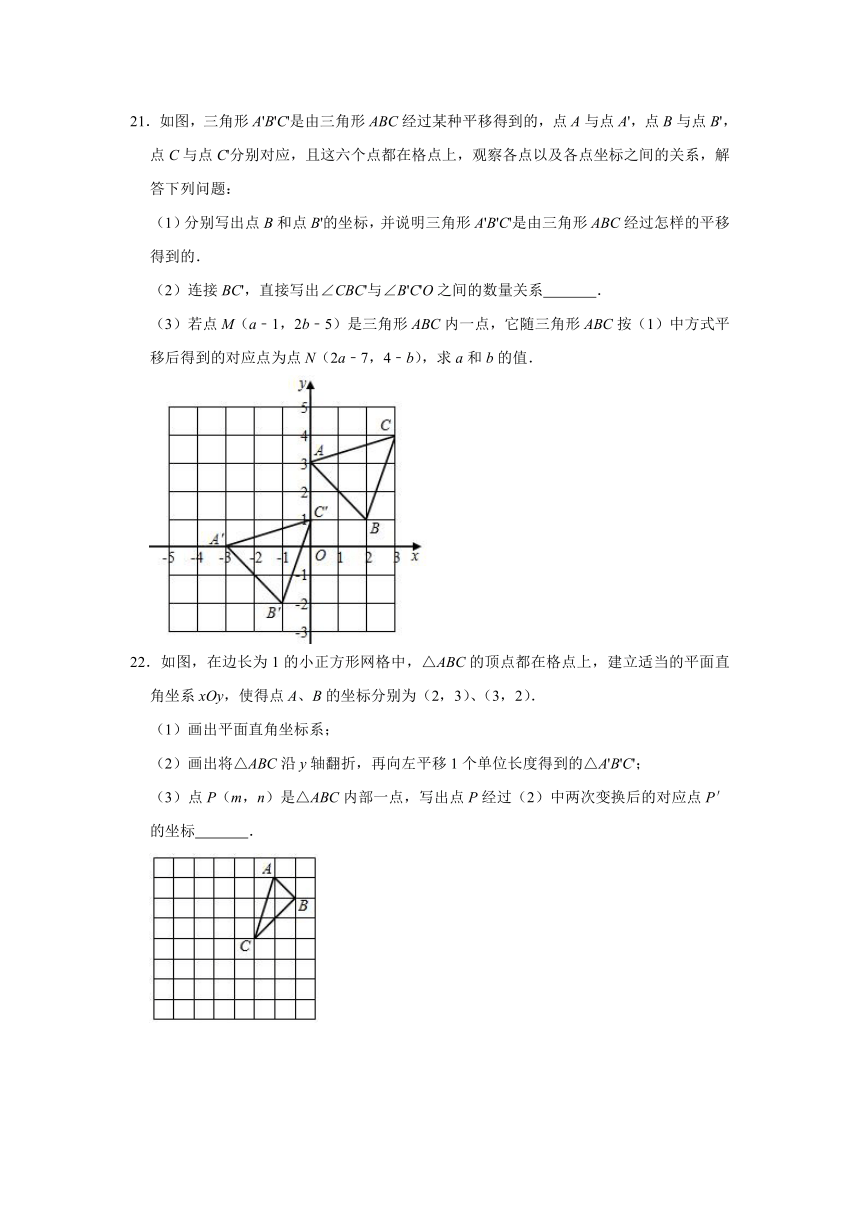
21.如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点B'的坐标,并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(2)连接BC',直接写出∠CBC'与∠B'C'O之间的数量关系
.
(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.
22.如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将△ABC沿y轴翻折,再向左平移1个单位长度得到的△A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中两次变换后的对应点P′的坐标
.
23.已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(5,6),B(﹣2,3),C(3,1).请在所给的平面直角坐标系中按要求完成以下问题:
(1)画出三角形ABC;
(2)将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形A1B1C1(点A1,B1,C1分别是点A,B,C移动后的对应点).
①请画出三角形A1B1C1;
②并判断线段AC与A1C1的位置与数量关系.
24.在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
25.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
26.如图,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上.
(1)求三角形ABC的面积;
(2)将△ABC平移后得到△DEF,若此时A点的对应点D的坐标为(1,3),请直接写出B点的对应点E和C点的对应点F的坐标,并在图中画出△DEF;
(3)在x轴上是否存在点P使得△DFP的面积与△ABC的面积相等,若存在,求出P点坐标,若不存在,请说明理由.
参考答案
1.解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
故选:A.
2.解:∵把△ABC沿RS的方向平移到△DEF的位置,BC=5,∠A=80°,∠B=70°,
∴CF=BE=4,∠F=∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣70°=30°,AB∥DE,
∴A、B、C正确,D错误,
故选:D.
3.解:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
4.解:点A(3,﹣1)的对应点C的坐标是(﹣2,5),可知横坐标由3变为﹣2,向左移动了5个单位,﹣1变为5,表示向上移动了6个单位,
于是点B(0,4)的对应点D的横坐标为0﹣5=﹣5,点D的纵坐标为4+6=10,
故D(﹣5,10).
故选:C.
5.解:①小朋友在荡秋千是旋转,不属于平移;
②打气筒打气时,活塞的运动,属于平移;
③钟摆的摆动是旋转,不属于平移;
④瓶装饮料在传送带上移动,属于平移.
故选:D.
6.解:∵点A(﹣2,3),A'(﹣5,7),
∴点A沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度得到点A′,
故选:D.
7.解:∵△ABC沿BC边向右平移3个单位,得到△DEF,
∴AD=BE=CF=3,AC=DF,
∵△ABC的周长为10,
∴AB+BC+AC=10,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=10+2×3=16.
故答案为16.
8.解:∵△ABC向右平移3cm得到△DEF,
∴BE=3cm,
∴CE=BC﹣BE=7﹣3=4(cm).
故答案为4.
9.解:∵三角形ABC沿着B到C的方向平移到三角形DEF的位置,平移距离是8,
∴S△ABC=S△DEF,DE=AB=10,BE=8,
∴HE=DE﹣DH=10﹣4=6,
∵S梯形ABEH+S△HEC=S△HEC+S阴影部分,
∴S阴影部分=S梯形ABEH=(6+10)×8=64.
故答案为64.
10.解:点(2,3)先向上爬2个单位长度,所得点的坐标为(2,5),
再向右爬4个单位长度,所得点的坐标为(6,5),
再向下爬1个单位长度后,所得点的坐标为(6,4),
故答案为:(6,4).
11.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
12.解:根据题意,得A的对应点为A′,B的对应点为B′,C的对应点为C′,
所以BC=B′C′,BB′=CC′,
∴四边形AB′C′C的周长=CA+AB+BB′+B′C′+C′C=△ABC的周长+2BB′=24+6=30cm.
故答案为:30cm.
13.解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移2个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+2),
即(3,﹣1),
故答案为:(3,﹣1).
14.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
15.解:∵△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,
∴CF=5,△ABC≌△DEF,
∴△ABC的边AC、AB所扫过的面积=S△ABC+S矩形BCFE﹣S△DEF
=S矩形BCFE
=4×5
=20(cm2).
故答案为20.
16.解:设凹槽的深度为a,
则第一个图形的周长为:2×(3+4)+2a=14+2a,
第二个图形的周长为2×(3+4)=14,
因此两个图形的周长不相等,
故答案为:不相等.
17.解:由图片可看出,剩余部分的草坪正好可以拼成一个长方形,且这个长方形的长为72﹣2=70m,这个长方形的宽为:31﹣1=30m,
因此草坪的面积=70×30=2100平方米.
故答案为:2100.
18.解:由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
19.解:(1)如图,△A1B1C1为所作;
(2)△A1B1C1的面积=4×2﹣×2×1﹣×1×4﹣×1×3=.
20.解:(1)如图,△A′B′C′即为所求作.
(2)△A′B′C′的面积=××=5.
(3)存在.设P(0,m),
由题意,×|2﹣m|×2=5,
解得m=7或﹣3,
∴P(0,7)或(0,﹣3).
21.解:(1)B(2,1),B′(﹣1,﹣2),
△A'B'C'是由△ABC向左平移3个单位长度,再向下平移3个单位长度得到的;
(2)由平移可得:∠CBC′=BC′B′,
∵∠BC′B′=∠BC′O+∠B′C′O=90°+∠B′C′O,
∴∠CBC'=90°+∠B′C′O;
(3)若M(a﹣1,2b﹣5)是三角形ABC内一点,它随△ABC按(1)中方式平移后得到对应点N(2a﹣7,4﹣b),
则a﹣1﹣3=2a﹣7,2b﹣5﹣3=4﹣b,
解得:a=3,b=4.
22.解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A′B′C′即为所求作.
(3)由题意,P′(﹣m﹣1,n).
故答案为:(﹣m﹣1,n).
23.解:(1)如图所示,△ABC即为所求;
(2)如图所示,A1B1C1即为所求,AC与A1C1平行且相等.
24.解:(1)如图,△ABC为所作;
(2)如图,△A′B′C′为所作;
(3)△A′B′C′的面积=6×4﹣×2×6﹣×2×4﹣×4×2=10.
25.解:(1)C(0,3),D(4,3)
S四边形ABDC=AB?OC=4×3=12;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,3),D(4,3),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
26.解:(1)△ABC的面积为5×5﹣×2×3﹣×3×5﹣×2×5=;
(2)∵点A(﹣1,4)的对应点D的坐标为(1,3),
∴点B(﹣4,﹣1)的对应点E的坐标为(﹣4+2,﹣1﹣1),即E(﹣2,﹣2);
点C(1,1)的对应点F的坐标为(1+2,1﹣1),即F(3,0);
△DEF如图所示:
(3)存在,设点P的坐标为(x,0),
由题意得,
解得或,
所以点P为(,0)或(,0)
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2)
B.(﹣3,﹣1)
C.(﹣3,4)
D.(﹣1,2)
2.如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )
A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5
3.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3( )
A.70°
B.180°
C.110°
D.80°
4.线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7)
B.(4,3)
C.(﹣5,10)
D.(﹣3,7)
5.下列现象中,属于平移的是( )
①小朋友在荡秋千;②打气筒打气时,活塞的运动;
③钟摆的摆动;④瓶装饮料在传送带上移动.
A.①②
B.①③
C.②③
D.②④
6.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
7.如图,将周长为10的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为
.
8.如图,将△ABC右平移3cm得到△DEF,点A与点D是对应点,点B与点E是对应点.如果BC=7cm,那么EC=
cm.
9.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,平移距离是8,则阴影部分的面积是
.
10.一只蚂蚁由点(2,3)先向上爬2个单位长度,再向右爬4个单位长度,再向下爬1个单位长度后,它所在位置的坐标是
.
11.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为
cm2.
12.如图,三角形ABC的周长为24cm,现将三角形ABC沿AB方向平移3cm至三角形A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是
.
13.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为
.
14.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a=
.
15.如图,△ABC中,BC=4cm.现将△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,则△ABC的边AC、AB所扫过的面积是
cm2.
16.如图,根据图中给出的数据判断两个图形的周长的关系:
.(填“相等”或“不相等”或“无法判断”).
17.如图是一块长方形的场地,长AB=72m,宽AD=31m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为
m2.
18.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为
.
19.如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位,再向下平移3个单位得到△A1B1C1.
(1)请在图中作出△A1B1C1;
(2)求△A1B1C1的面积.
20.如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).
(1)将△ABC向右平移3个单位,作出△A′B′C′;
(2)写出△A′B′C′的面积;
(3)在y轴上是否存在点P,使得△APC的面积与△ABC的面积相等,若存在,求出P点的坐标;若不存在,说明理由.
21.如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点B'的坐标,并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(2)连接BC',直接写出∠CBC'与∠B'C'O之间的数量关系
.
(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.
22.如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将△ABC沿y轴翻折,再向左平移1个单位长度得到的△A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中两次变换后的对应点P′的坐标
.
23.已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(5,6),B(﹣2,3),C(3,1).请在所给的平面直角坐标系中按要求完成以下问题:
(1)画出三角形ABC;
(2)将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形A1B1C1(点A1,B1,C1分别是点A,B,C移动后的对应点).
①请画出三角形A1B1C1;
②并判断线段AC与A1C1的位置与数量关系.
24.在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
25.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
26.如图,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上.
(1)求三角形ABC的面积;
(2)将△ABC平移后得到△DEF,若此时A点的对应点D的坐标为(1,3),请直接写出B点的对应点E和C点的对应点F的坐标,并在图中画出△DEF;
(3)在x轴上是否存在点P使得△DFP的面积与△ABC的面积相等,若存在,求出P点坐标,若不存在,请说明理由.
参考答案
1.解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
故选:A.
2.解:∵把△ABC沿RS的方向平移到△DEF的位置,BC=5,∠A=80°,∠B=70°,
∴CF=BE=4,∠F=∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣70°=30°,AB∥DE,
∴A、B、C正确,D错误,
故选:D.
3.解:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
4.解:点A(3,﹣1)的对应点C的坐标是(﹣2,5),可知横坐标由3变为﹣2,向左移动了5个单位,﹣1变为5,表示向上移动了6个单位,
于是点B(0,4)的对应点D的横坐标为0﹣5=﹣5,点D的纵坐标为4+6=10,
故D(﹣5,10).
故选:C.
5.解:①小朋友在荡秋千是旋转,不属于平移;
②打气筒打气时,活塞的运动,属于平移;
③钟摆的摆动是旋转,不属于平移;
④瓶装饮料在传送带上移动,属于平移.
故选:D.
6.解:∵点A(﹣2,3),A'(﹣5,7),
∴点A沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度得到点A′,
故选:D.
7.解:∵△ABC沿BC边向右平移3个单位,得到△DEF,
∴AD=BE=CF=3,AC=DF,
∵△ABC的周长为10,
∴AB+BC+AC=10,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=10+2×3=16.
故答案为16.
8.解:∵△ABC向右平移3cm得到△DEF,
∴BE=3cm,
∴CE=BC﹣BE=7﹣3=4(cm).
故答案为4.
9.解:∵三角形ABC沿着B到C的方向平移到三角形DEF的位置,平移距离是8,
∴S△ABC=S△DEF,DE=AB=10,BE=8,
∴HE=DE﹣DH=10﹣4=6,
∵S梯形ABEH+S△HEC=S△HEC+S阴影部分,
∴S阴影部分=S梯形ABEH=(6+10)×8=64.
故答案为64.
10.解:点(2,3)先向上爬2个单位长度,所得点的坐标为(2,5),
再向右爬4个单位长度,所得点的坐标为(6,5),
再向下爬1个单位长度后,所得点的坐标为(6,4),
故答案为:(6,4).
11.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
12.解:根据题意,得A的对应点为A′,B的对应点为B′,C的对应点为C′,
所以BC=B′C′,BB′=CC′,
∴四边形AB′C′C的周长=CA+AB+BB′+B′C′+C′C=△ABC的周长+2BB′=24+6=30cm.
故答案为:30cm.
13.解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移2个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+2),
即(3,﹣1),
故答案为:(3,﹣1).
14.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
15.解:∵△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,
∴CF=5,△ABC≌△DEF,
∴△ABC的边AC、AB所扫过的面积=S△ABC+S矩形BCFE﹣S△DEF
=S矩形BCFE
=4×5
=20(cm2).
故答案为20.
16.解:设凹槽的深度为a,
则第一个图形的周长为:2×(3+4)+2a=14+2a,
第二个图形的周长为2×(3+4)=14,
因此两个图形的周长不相等,
故答案为:不相等.
17.解:由图片可看出,剩余部分的草坪正好可以拼成一个长方形,且这个长方形的长为72﹣2=70m,这个长方形的宽为:31﹣1=30m,
因此草坪的面积=70×30=2100平方米.
故答案为:2100.
18.解:由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
19.解:(1)如图,△A1B1C1为所作;
(2)△A1B1C1的面积=4×2﹣×2×1﹣×1×4﹣×1×3=.
20.解:(1)如图,△A′B′C′即为所求作.
(2)△A′B′C′的面积=××=5.
(3)存在.设P(0,m),
由题意,×|2﹣m|×2=5,
解得m=7或﹣3,
∴P(0,7)或(0,﹣3).
21.解:(1)B(2,1),B′(﹣1,﹣2),
△A'B'C'是由△ABC向左平移3个单位长度,再向下平移3个单位长度得到的;
(2)由平移可得:∠CBC′=BC′B′,
∵∠BC′B′=∠BC′O+∠B′C′O=90°+∠B′C′O,
∴∠CBC'=90°+∠B′C′O;
(3)若M(a﹣1,2b﹣5)是三角形ABC内一点,它随△ABC按(1)中方式平移后得到对应点N(2a﹣7,4﹣b),
则a﹣1﹣3=2a﹣7,2b﹣5﹣3=4﹣b,
解得:a=3,b=4.
22.解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A′B′C′即为所求作.
(3)由题意,P′(﹣m﹣1,n).
故答案为:(﹣m﹣1,n).
23.解:(1)如图所示,△ABC即为所求;
(2)如图所示,A1B1C1即为所求,AC与A1C1平行且相等.
24.解:(1)如图,△ABC为所作;
(2)如图,△A′B′C′为所作;
(3)△A′B′C′的面积=6×4﹣×2×6﹣×2×4﹣×4×2=10.
25.解:(1)C(0,3),D(4,3)
S四边形ABDC=AB?OC=4×3=12;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,3),D(4,3),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
26.解:(1)△ABC的面积为5×5﹣×2×3﹣×3×5﹣×2×5=;
(2)∵点A(﹣1,4)的对应点D的坐标为(1,3),
∴点B(﹣4,﹣1)的对应点E的坐标为(﹣4+2,﹣1﹣1),即E(﹣2,﹣2);
点C(1,1)的对应点F的坐标为(1+2,1﹣1),即F(3,0);
△DEF如图所示:
(3)存在,设点P的坐标为(x,0),
由题意得,
解得或,
所以点P为(,0)或(,0)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
