2020-2021学年北师大版八年级数学下册3.2图形的旋转-同步提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.2图形的旋转-同步提升训练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 369.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 11:58:45 | ||
图片预览



文档简介
2020-2021年度北师大版八年级数学下册《3.2图形的旋转》同步提升训练(附答案)
1.如图,在△ABC中,AB=3,BC=5.2,∠B=60°,将△ABC绕点A逆时针旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为( )
A.0.8
B.2
C.2.2
D.2.8
2.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°)将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,下列结论中:①若∠DCE=35°,∠ACB=145°;②∠ACB+∠DCE=180°;③当三角尺BCE的边与AD平行时∠ACE=30°或120°;④当三角尺BCE的边与AD垂直时∠ACE=30°或75°或120°,正确个数有( )
A.4个
B.3个
C.2个
D.1个
3.如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AE=EC
B.AB=CD
C.∠B=∠D
D.∠AEF=∠B
4.如图,将△ABC纸片绕点C顺时针旋转40°得到△A'B'C,连接AA',若AC⊥A'B',则∠AA'B'的度数为( )
A.20°
B.40°
C.50°
D.60°
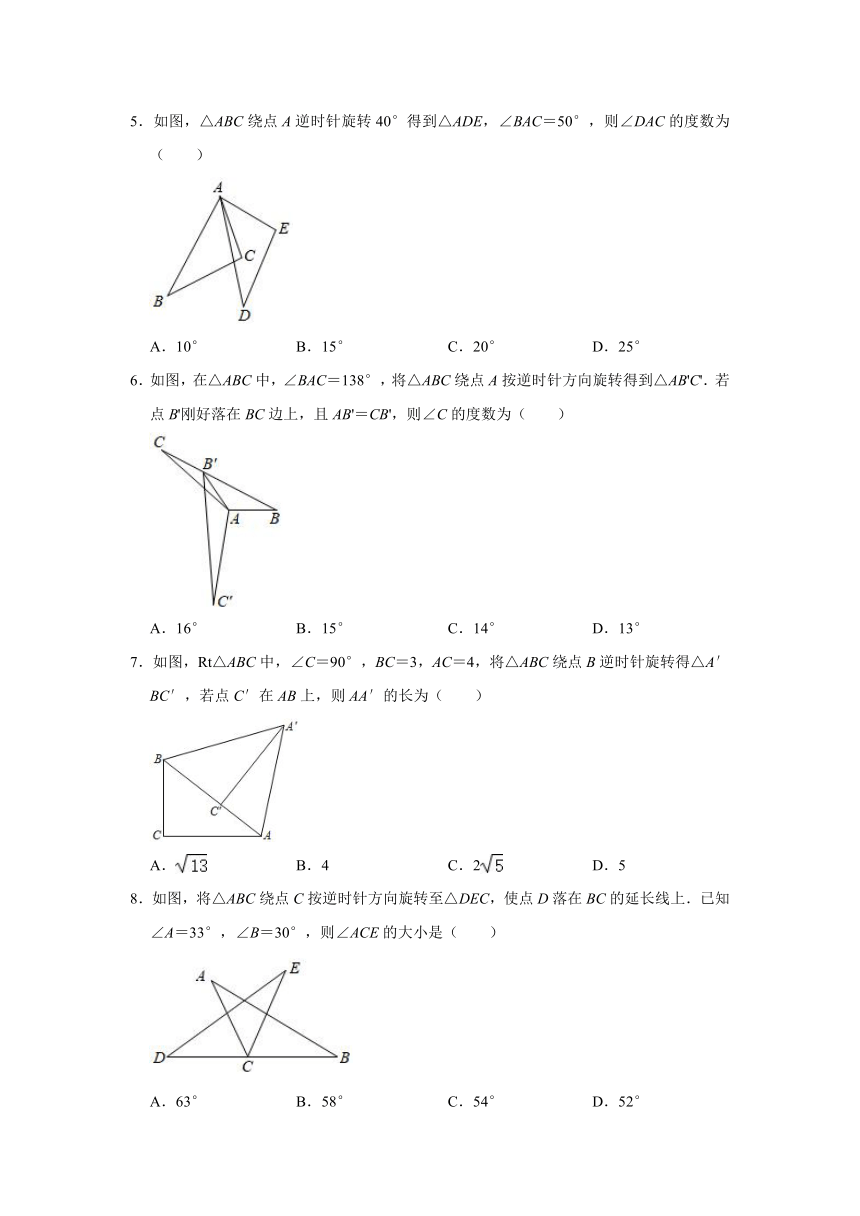
5.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10°
B.15°
C.20°
D.25°
6.如图,在△ABC中,∠BAC=138°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C的度数为( )
A.16°
B.15°
C.14°
D.13°
7.如图,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为( )
A.
B.4
C.2
D.5
8.如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( )
A.63°
B.58°
C.54°
D.52°
9.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.下列结论一定正确的是( )
A.BC=BD
B.AB⊥AE
C.AC=DE
D.∠A=∠EBC
10.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图②所示,则旋转角∠BAD的度数为( )
A.15°
B.30°
C.45°
D.60°
11.如图.将△ABC绕点A逆时针旋转90°得到△ADE,连接BE,若∠CBE=75°,则∠BED的度数是
.
12.如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是
.
13.如图,P是等边△ABC内一点,PA=4,PB=2,PC=2,则△ABC的边长为
.
14.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE=
.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:
(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;
(4)四边形PMON的面积不变,其中正确的序号为
.
16.如图,P是等边三角形ABC内一点将△ACP绕点A顺时针旋转60°得到△ABQ,连接BP若PA=2,PB=4,PC=2,则四边形APBQ的面积为
.
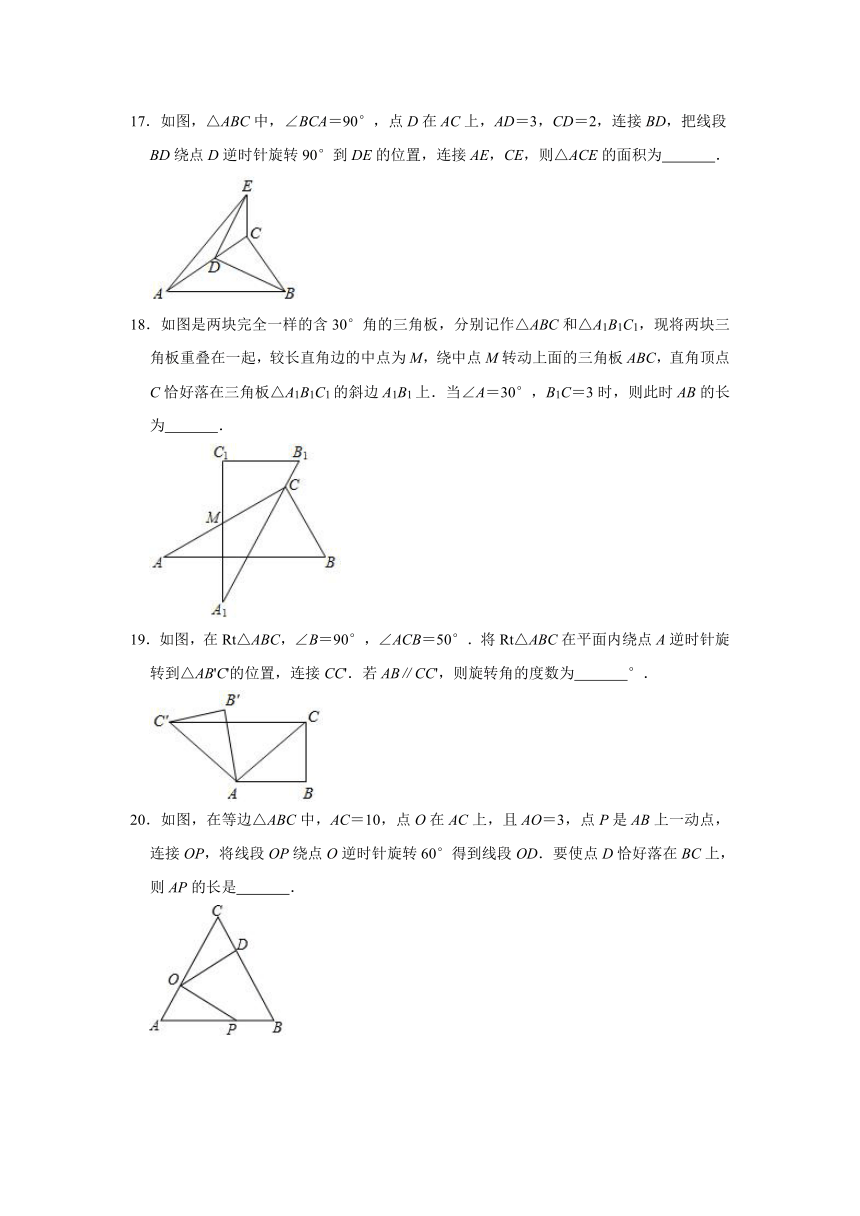
17.如图,△ABC中,∠BCA=90°,点D在AC上,AD=3,CD=2,连接BD,把线段BD绕点D逆时针旋转90°到DE的位置,连接AE,CE,则△ACE的面积为
.
18.如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=3时,则此时AB的长为
.
19.如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,连接CC'.若AB∥CC',则旋转角的度数为
°.
20.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是
.
21.如图,Rt△ABC中,∠ACB=90°,∠A=60°,△ABC绕点C顺时针旋转60°,得到△DCE.
(1)求证:DE垂直平分BC;
(2)F是DE中点,连接BF,CF,若AC=2,求四边形ACFB的面积.
22.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(﹣3,2)、B(0,2)、C(﹣1,0)(正方形网格中每个小正方形的边长是一个单位长度).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)请画出△ABC以点O为旋转中心,逆时针旋转90°所得△A2B2C2.
23.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为E,点A的对应点D落在线段AB上,DE与BC相交于点F,连接BE.
(Ⅰ)求证:DC平分∠ADE;
(Ⅱ)试判断BE与AB的位置关系,并说明理由;
(Ⅲ)若BE=BD,求∠ABC的大小.(直接写出结果即可)
24.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
25.如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°(sin37°=0.6).
(1)求∠ADC的大小;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
26.(1)如图①,△ABC是等边三角形,M为边BC的中点,连接AM,将线段AM顺时针旋转120°,得到线段AD,连接BD;点N在BC的延长线上,且CN=MC,连接AN.
求证:BD=AN.
(2)若将问题(1)中的条件“M为边BC的中点”改为“M为边BC上的任意一点”,其他条件不变,结论还成立吗?如果成立,请画出图形并给出证明;如果不成立,请举出反例.
参考答案
1.解:∵将△ABC绕点A逆时针旋转得到△ADE,
∴AB=AD=3,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB=3,
∴CD=BC﹣BD=5.2﹣3=2.2,
故选:C.
2.解:①∵∠ACD=∠ECB=90°,∠DCE=35°,
∴∠ACB=180°﹣35°=145°.
故①正确;
②∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°.
故②正确;
③如图1中,当AD∥BC时.
∵AD∥BC,
∴∠D=∠BCD=30°,
∵∠ACE+∠ECD=∠ECD+∠DCB=90°,
∴∠ACE=∠DCB=30°.
如图2中,当AD∥CE时,∠DCE=∠D=30°,可得∠ACE=90°+30°=120°.
如图3中,当AD∥BE时,延长BC交AD于M.
∵AD∥BE,
∴∠AMC=∠B=45°,
∴∠ACM=180°﹣60°﹣45°=75°,
∴∠ACE=75°+90°=165°,
综上所述,满足条件的∠ACE的度数为30°或120°或165°.
故③错误.
④如图4,当AD⊥EC时,
∵AD⊥BC,∠A=60°,
∴∠ACE=30°,
如图5,当AD⊥BE时,
∵BE⊥AD,
∴∠ACE=360°﹣∠A﹣∠B﹣∠ECB﹣90°,
∴∠ACE=360°﹣60°﹣45°﹣90°﹣90°=75°,
如图6,当BC⊥AD于点F,
∴∠FCE=∠DCA=90°,
∴∠DCE=∠ACF=30°,
∴∠ACE=120°,
故∠ACE=30°或75°或120°.
故④正确.
故选:B.
3.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴△ABC≌△DEC,
∴BC=CE,AB=DE,BC=EC,∠B=∠CED,∠A=∠D,
∴∠AEF=∠CED=∠B,
故选:D.
4.解:若AC⊥A1B1,垂足为D,
∵AC⊥A1B1,
∴直角△A1CD中,∠DA1C=90°﹣∠DCA1=90°﹣40°=50°.
∵CA=CA1,
∴∠CAA1=∠CA1A===70°,
∴∠AA1B=70°﹣50°=20°.
故选:A.
5.解:由旋转的性质可知,∠BAD=40°,
∵∠BAC=50°,
∴∠DAC=∠BAC﹣∠BAD=50°﹣40°=10°,
故选:A.
6.解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣138°,
∴∠C=14°,
∴∠C'=∠C=14°,
故选:C.
7.解:根据旋转可知:
∠A′C′B=∠C=90°,A′C′=AC=4,AB=A′B,
根据勾股定理,得AB===5,
∴A′B=AB=5,
∴AC′=AB﹣BC′=2,
在Rt△AA′C′中,根据勾股定理,得
AA′===2.
故选:C.
8.解:∵∠A=33°,∠B=30°,
∴∠ACD=∠A+∠B=33°+30°=63°,
∵△ABC绕点C按逆时针方向旋转至△DEC,
∴△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD,
∴∠BCE=63°,
∴∠ACE=180°﹣∠ACD﹣∠BCE=180°﹣63°﹣63°=54°.
故选:C.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠ACD=∠BCE,AC=DC,BC=EC,
∴∠A=,∠EBC=,
∴∠A=∠EBC,
故选:D.
10.解:如图,设AD与BC交于点F,
∵BC∥DE,
∴∠CFA=∠D=90°,
∵∠CFA=∠B+∠BAD=60°+∠BAD,
∴∠BAD=30°故选:B.
11.解:如图,延长ED交BC于H,
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴∠ADE=∠ABC,∠BAD=90°,
∴∠ADE+∠DAE+∠AED=180°=∠ABC+∠DAE+∠AED,
∵∠ABC+∠BHE+∠AED+∠BAD+∠DAE=360°,
∴∠BHE=90°,
∵∠CBE=75°,
∴∠BED=15°,
故答案为15°.
12.解:如图,连接AC,AE,BE,
∵EF=2,BF=3,
∴BE===,
∵∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵将边DA绕点D逆时针旋转60°得到线段DE,
∴AD=AE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴∠DAE=∠BAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD=,
故答案为:.
13.解:作BH⊥PC于H,如图,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2,∠PBD=60°,
∴△PBD为等边三角形,
∴PD=PB=2,∠BPD=60°,
在△PDC中,PC=2,PD=2,CD=4,
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∠BPH=30°,PB=2,
∴BH=PB=,PH=BH=3,
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=()2+52=28,
∴BC=2,
故答案为:2
14.解:如图,连接AD.
在Rt△ADF和Rt△ADC中,
,
∴Rt△ADF≌Rt△ADC(HL),
∴DF=DC,
∵BD=5,BC=4,
∴CD=DF﹣5﹣4=1,
∵EF=BC=4,
∴DE=EF﹣DF=4﹣1=3.
故答案为:3.
15.解:如图作PE⊥OA于E,PF⊥OB于F.
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在△POE和△POF中,
,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,故(1)正确,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故(4)正确,
∵OM﹣ON=OE+EM﹣(OF﹣FN)=2EM,不是定值,故(2)错误,
∵OM+ON=OE+ME+OF﹣NF=2OE=定值,
在旋转过程中,△PMN是等腰三角形,形状是相似的,因为PM的长度是变化的,所以MN的长度是变化的,所以△OMN的周长是变化的,故(3)错误,
故答案为(1)(4).
16.解:如图,连接PQ.
∵△ACP绕点A顺时针旋转60°得到△ABQ,
∴AP=AQ=2,PC=BQ=2,∠PAQ=60°,
∴△PAQ是等边三角形,
∴PQ=PA=2,
∵PB=4,
∴PB2=BQ2+PQ2,
∴∠PQB=90°,
∴S四边形APBQ=S△PBQ+S△APQ=?PQ?QB+?PA2=×2×2+×4=3,
故答案为3.
17.解:∵把线段BD绕点D逆时针旋转90°到DE的位置,
∴DE=DB,∠BDE=90°,
如图,将△DCB绕点D逆时针旋转90°得△DFE,
∴∠FDC=90°,CD=DF=2,∠EFD=∠ACB=90°,
∴∠EFD+∠FDC=180°,
∴EF∥CD,
∴△ACE的面积=×AD×DF=×5×2=5,
故答案为:5.
18.解:连接C1C,
∵M是AC的中点,△ABC,△A1B1C1是两块完全一样的含30°角三角板重叠在一起的,
∴AM=CM=A1C1,
即CM=A1M=C1M,
∴∠A1=∠1,∠2=∠3,
∴A1+∠3=∠1+∠2=90°=∠A1CC1,
∴△B1C1C为直角三角形,
∵∠A1=30°,
∴∠B1=60°,
∴∠B1C1C=30°,
∴BC=B1C1=2B1C=6,
∵∠A=30°,
∴AB=2BC=12.
故答案为:12.
19.解:∵AB∥CC',
∴∠ABC+∠C′CB=180°,
而∠B=90°,
∴∠C′CB=90°,
∴∠ACC′=90°﹣∠ACB=90°﹣50°=40°,
∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,
∴AC=AC′,∠C′AC等于旋转角,
∴∠AC′C=∠ACC′=40°,
∴∠C′AC=180°﹣40°﹣40°=100°,
即旋转角为100°.
故答案为100.
20.解:∵AC=10,AO=3,
∴OC=7,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠AOP+∠APO+∠A=180°,∠AOP+∠COD+∠POD=180°,
∴∠AOP+∠APO=120°,∠AOP+∠COD=120°,
∴∠APO=∠COD,
在△AOP和△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=7.
故答案为:7.
21.证明:(1)如图,设BC与DE交于点O,
∵△ABC绕点C顺时针旋转60°,得到△DCE,
∴CD=AC,∠A=∠CDE=60°,∠ACD=60°,AB=DE,
∴△ACD是等边三角形,DE∥AC,
∴∠ACB=∠DOB=90°,AD=CD=AC,
∵∠ACB=90°,∠A=60°,
∴∠B=∠DCB=30°,
∴CD=BD,
∴DE垂直平分BC;
(2)∵∠ABC=30°,∠ACB=90°,AC=2,
∴BC=AC=2,AB=2AC=4,
∴S△ACB=×AC×BC=×2×2=2,
∵AD=BD,
∴S△ADC=S△ABC=×2=,
∵F是DE中点,
∴DF=EF=CF=DE=AB=2,
∴S四边形BDCF=×BC×DF=2,
∴四边形ACFB的面积=2+=3.
22.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作.
23.(Ⅰ)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE,
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(Ⅱ)解:结论:BE⊥AB.
由旋转的性质可知,∠ACD=∠BCE,
∵CA=CD,CB=CE,
∴∠CAD=∠CDA=∠CBE=∠CEB,
∵∠ABC+∠CAB+∠ACD+∠DCB=180°,
∴∠ABC+∠CBE+∠DCB+∠BCE=180°,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(Ⅲ)如图,设BC交DE于O.连接AO,过点B作BH⊥CD交CD的延长线于H,作BT⊥CE于T,
∵∠H=∠BTC=∠HCT=90°,
∴∠HBT=∠DBE=90°,
∴∠DBH=∠EBT,
∵BD=BE,∠H=∠BTE=90°
∴△BHD≌△BTE(AAS),
∴BH=BT,
∵BH⊥CH,BT⊥CE,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°.
24.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
25.解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠CAB=∠DAE=60°,
∵∠BFD=97°=∠AFE,
∴∠E=180°﹣97°﹣60°=23°,
∴∠ADC=∠E=23°;
(2)如图,连接DE,
∵AD=AE,∠DAE=60°,
∴△AED是等边三角形,
∴∠ADE=60°,AD=DE,
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE,
∴CD=BE=5,
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,
∴DE===4,
∴AD=DE=4.
26.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,AB=BC=AC,
∵又M是BC的中点,
∴∠AMB=∠AMN=90°,BC=2BM=2MC,∠BAM=∠BAC=30°,
∵AM顺时针旋转120°得到线段AB,
∴∠MAD=120°,AD=AM,
∴∠BAD=∠MAD﹣∠BAM=120°﹣30°=90°,
∴∠BAD=∠AMN=90°,
∵MC=CN,
∴MN=2MC=BC=AB,
在△DBA和△ANM中,
,
∴△DBA≌△ANM(SAS),
∴BD=AN.
(2)结论成立,理由如下:
①如图②﹣1中,当BM>BC时,分别过点A、点D作AG⊥BM、DH⊥BA垂足分别为G、H.
∴∠DHA=∠AGM=90°,
∵∠AMG+∠BAM+∠ABC=180°,∠ABC=160°,
∴∠AMG=180°﹣∠ABC﹣∠BAM=120°﹣∠BAM,
∵AM顺时针旋转120°得到线段AB,
∴∠MAD=120°,AD=AM,
∴∠DAB=120°﹣∠BAM,
∴∠DAB=∠AMB,
在△DAH和△AMG中,
,
∴△DAH≌△AMG(AAS),
∴DH=AG,AH=GM,
又∵△ABC是等边三角形,AG⊥BM,
∴BG=GC,
∴GN=GC+CN=GC+CM=BG+GC﹣GM=BC﹣GM,
又∵BH=AB﹣HA,AH=GM,AB=BC,
∴BH=GN.
∵DH=AG,∠DHA=∠AGM=90°,BH=GN,
在△DBH和△ANG中,
∴△DBH≌△ANG(SAS),
∴BD=AN.
②当BM<BC时,同法可得BD=AN.
1.如图,在△ABC中,AB=3,BC=5.2,∠B=60°,将△ABC绕点A逆时针旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为( )
A.0.8
B.2
C.2.2
D.2.8
2.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°)将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,下列结论中:①若∠DCE=35°,∠ACB=145°;②∠ACB+∠DCE=180°;③当三角尺BCE的边与AD平行时∠ACE=30°或120°;④当三角尺BCE的边与AD垂直时∠ACE=30°或75°或120°,正确个数有( )
A.4个
B.3个
C.2个
D.1个
3.如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AE=EC
B.AB=CD
C.∠B=∠D
D.∠AEF=∠B
4.如图,将△ABC纸片绕点C顺时针旋转40°得到△A'B'C,连接AA',若AC⊥A'B',则∠AA'B'的度数为( )
A.20°
B.40°
C.50°
D.60°
5.如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
A.10°
B.15°
C.20°
D.25°
6.如图,在△ABC中,∠BAC=138°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'刚好落在BC边上,且AB'=CB',则∠C的度数为( )
A.16°
B.15°
C.14°
D.13°
7.如图,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为( )
A.
B.4
C.2
D.5
8.如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( )
A.63°
B.58°
C.54°
D.52°
9.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.下列结论一定正确的是( )
A.BC=BD
B.AB⊥AE
C.AC=DE
D.∠A=∠EBC
10.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图②所示,则旋转角∠BAD的度数为( )
A.15°
B.30°
C.45°
D.60°
11.如图.将△ABC绕点A逆时针旋转90°得到△ADE,连接BE,若∠CBE=75°,则∠BED的度数是
.
12.如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是
.
13.如图,P是等边△ABC内一点,PA=4,PB=2,PC=2,则△ABC的边长为
.
14.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE=
.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:
(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;
(4)四边形PMON的面积不变,其中正确的序号为
.
16.如图,P是等边三角形ABC内一点将△ACP绕点A顺时针旋转60°得到△ABQ,连接BP若PA=2,PB=4,PC=2,则四边形APBQ的面积为
.
17.如图,△ABC中,∠BCA=90°,点D在AC上,AD=3,CD=2,连接BD,把线段BD绕点D逆时针旋转90°到DE的位置,连接AE,CE,则△ACE的面积为
.
18.如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=3时,则此时AB的长为
.
19.如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,连接CC'.若AB∥CC',则旋转角的度数为
°.
20.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是
.
21.如图,Rt△ABC中,∠ACB=90°,∠A=60°,△ABC绕点C顺时针旋转60°,得到△DCE.
(1)求证:DE垂直平分BC;
(2)F是DE中点,连接BF,CF,若AC=2,求四边形ACFB的面积.
22.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(﹣3,2)、B(0,2)、C(﹣1,0)(正方形网格中每个小正方形的边长是一个单位长度).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)请画出△ABC以点O为旋转中心,逆时针旋转90°所得△A2B2C2.
23.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为E,点A的对应点D落在线段AB上,DE与BC相交于点F,连接BE.
(Ⅰ)求证:DC平分∠ADE;
(Ⅱ)试判断BE与AB的位置关系,并说明理由;
(Ⅲ)若BE=BD,求∠ABC的大小.(直接写出结果即可)
24.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
25.如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°(sin37°=0.6).
(1)求∠ADC的大小;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
26.(1)如图①,△ABC是等边三角形,M为边BC的中点,连接AM,将线段AM顺时针旋转120°,得到线段AD,连接BD;点N在BC的延长线上,且CN=MC,连接AN.
求证:BD=AN.
(2)若将问题(1)中的条件“M为边BC的中点”改为“M为边BC上的任意一点”,其他条件不变,结论还成立吗?如果成立,请画出图形并给出证明;如果不成立,请举出反例.
参考答案
1.解:∵将△ABC绕点A逆时针旋转得到△ADE,
∴AB=AD=3,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB=3,
∴CD=BC﹣BD=5.2﹣3=2.2,
故选:C.
2.解:①∵∠ACD=∠ECB=90°,∠DCE=35°,
∴∠ACB=180°﹣35°=145°.
故①正确;
②∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°.
故②正确;
③如图1中,当AD∥BC时.
∵AD∥BC,
∴∠D=∠BCD=30°,
∵∠ACE+∠ECD=∠ECD+∠DCB=90°,
∴∠ACE=∠DCB=30°.
如图2中,当AD∥CE时,∠DCE=∠D=30°,可得∠ACE=90°+30°=120°.
如图3中,当AD∥BE时,延长BC交AD于M.
∵AD∥BE,
∴∠AMC=∠B=45°,
∴∠ACM=180°﹣60°﹣45°=75°,
∴∠ACE=75°+90°=165°,
综上所述,满足条件的∠ACE的度数为30°或120°或165°.
故③错误.
④如图4,当AD⊥EC时,
∵AD⊥BC,∠A=60°,
∴∠ACE=30°,
如图5,当AD⊥BE时,
∵BE⊥AD,
∴∠ACE=360°﹣∠A﹣∠B﹣∠ECB﹣90°,
∴∠ACE=360°﹣60°﹣45°﹣90°﹣90°=75°,
如图6,当BC⊥AD于点F,
∴∠FCE=∠DCA=90°,
∴∠DCE=∠ACF=30°,
∴∠ACE=120°,
故∠ACE=30°或75°或120°.
故④正确.
故选:B.
3.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴△ABC≌△DEC,
∴BC=CE,AB=DE,BC=EC,∠B=∠CED,∠A=∠D,
∴∠AEF=∠CED=∠B,
故选:D.
4.解:若AC⊥A1B1,垂足为D,
∵AC⊥A1B1,
∴直角△A1CD中,∠DA1C=90°﹣∠DCA1=90°﹣40°=50°.
∵CA=CA1,
∴∠CAA1=∠CA1A===70°,
∴∠AA1B=70°﹣50°=20°.
故选:A.
5.解:由旋转的性质可知,∠BAD=40°,
∵∠BAC=50°,
∴∠DAC=∠BAC﹣∠BAD=50°﹣40°=10°,
故选:A.
6.解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣138°,
∴∠C=14°,
∴∠C'=∠C=14°,
故选:C.
7.解:根据旋转可知:
∠A′C′B=∠C=90°,A′C′=AC=4,AB=A′B,
根据勾股定理,得AB===5,
∴A′B=AB=5,
∴AC′=AB﹣BC′=2,
在Rt△AA′C′中,根据勾股定理,得
AA′===2.
故选:C.
8.解:∵∠A=33°,∠B=30°,
∴∠ACD=∠A+∠B=33°+30°=63°,
∵△ABC绕点C按逆时针方向旋转至△DEC,
∴△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD,
∴∠BCE=63°,
∴∠ACE=180°﹣∠ACD﹣∠BCE=180°﹣63°﹣63°=54°.
故选:C.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠ACD=∠BCE,AC=DC,BC=EC,
∴∠A=,∠EBC=,
∴∠A=∠EBC,
故选:D.
10.解:如图,设AD与BC交于点F,
∵BC∥DE,
∴∠CFA=∠D=90°,
∵∠CFA=∠B+∠BAD=60°+∠BAD,
∴∠BAD=30°故选:B.
11.解:如图,延长ED交BC于H,
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴∠ADE=∠ABC,∠BAD=90°,
∴∠ADE+∠DAE+∠AED=180°=∠ABC+∠DAE+∠AED,
∵∠ABC+∠BHE+∠AED+∠BAD+∠DAE=360°,
∴∠BHE=90°,
∵∠CBE=75°,
∴∠BED=15°,
故答案为15°.
12.解:如图,连接AC,AE,BE,
∵EF=2,BF=3,
∴BE===,
∵∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵将边DA绕点D逆时针旋转60°得到线段DE,
∴AD=AE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴∠DAE=∠BAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD=,
故答案为:.
13.解:作BH⊥PC于H,如图,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2,∠PBD=60°,
∴△PBD为等边三角形,
∴PD=PB=2,∠BPD=60°,
在△PDC中,PC=2,PD=2,CD=4,
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∠BPH=30°,PB=2,
∴BH=PB=,PH=BH=3,
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=()2+52=28,
∴BC=2,
故答案为:2
14.解:如图,连接AD.
在Rt△ADF和Rt△ADC中,
,
∴Rt△ADF≌Rt△ADC(HL),
∴DF=DC,
∵BD=5,BC=4,
∴CD=DF﹣5﹣4=1,
∵EF=BC=4,
∴DE=EF﹣DF=4﹣1=3.
故答案为:3.
15.解:如图作PE⊥OA于E,PF⊥OB于F.
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在△POE和△POF中,
,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,故(1)正确,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故(4)正确,
∵OM﹣ON=OE+EM﹣(OF﹣FN)=2EM,不是定值,故(2)错误,
∵OM+ON=OE+ME+OF﹣NF=2OE=定值,
在旋转过程中,△PMN是等腰三角形,形状是相似的,因为PM的长度是变化的,所以MN的长度是变化的,所以△OMN的周长是变化的,故(3)错误,
故答案为(1)(4).
16.解:如图,连接PQ.
∵△ACP绕点A顺时针旋转60°得到△ABQ,
∴AP=AQ=2,PC=BQ=2,∠PAQ=60°,
∴△PAQ是等边三角形,
∴PQ=PA=2,
∵PB=4,
∴PB2=BQ2+PQ2,
∴∠PQB=90°,
∴S四边形APBQ=S△PBQ+S△APQ=?PQ?QB+?PA2=×2×2+×4=3,
故答案为3.
17.解:∵把线段BD绕点D逆时针旋转90°到DE的位置,
∴DE=DB,∠BDE=90°,
如图,将△DCB绕点D逆时针旋转90°得△DFE,
∴∠FDC=90°,CD=DF=2,∠EFD=∠ACB=90°,
∴∠EFD+∠FDC=180°,
∴EF∥CD,
∴△ACE的面积=×AD×DF=×5×2=5,
故答案为:5.
18.解:连接C1C,
∵M是AC的中点,△ABC,△A1B1C1是两块完全一样的含30°角三角板重叠在一起的,
∴AM=CM=A1C1,
即CM=A1M=C1M,
∴∠A1=∠1,∠2=∠3,
∴A1+∠3=∠1+∠2=90°=∠A1CC1,
∴△B1C1C为直角三角形,
∵∠A1=30°,
∴∠B1=60°,
∴∠B1C1C=30°,
∴BC=B1C1=2B1C=6,
∵∠A=30°,
∴AB=2BC=12.
故答案为:12.
19.解:∵AB∥CC',
∴∠ABC+∠C′CB=180°,
而∠B=90°,
∴∠C′CB=90°,
∴∠ACC′=90°﹣∠ACB=90°﹣50°=40°,
∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,
∴AC=AC′,∠C′AC等于旋转角,
∴∠AC′C=∠ACC′=40°,
∴∠C′AC=180°﹣40°﹣40°=100°,
即旋转角为100°.
故答案为100.
20.解:∵AC=10,AO=3,
∴OC=7,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠AOP+∠APO+∠A=180°,∠AOP+∠COD+∠POD=180°,
∴∠AOP+∠APO=120°,∠AOP+∠COD=120°,
∴∠APO=∠COD,
在△AOP和△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=7.
故答案为:7.
21.证明:(1)如图,设BC与DE交于点O,
∵△ABC绕点C顺时针旋转60°,得到△DCE,
∴CD=AC,∠A=∠CDE=60°,∠ACD=60°,AB=DE,
∴△ACD是等边三角形,DE∥AC,
∴∠ACB=∠DOB=90°,AD=CD=AC,
∵∠ACB=90°,∠A=60°,
∴∠B=∠DCB=30°,
∴CD=BD,
∴DE垂直平分BC;
(2)∵∠ABC=30°,∠ACB=90°,AC=2,
∴BC=AC=2,AB=2AC=4,
∴S△ACB=×AC×BC=×2×2=2,
∵AD=BD,
∴S△ADC=S△ABC=×2=,
∵F是DE中点,
∴DF=EF=CF=DE=AB=2,
∴S四边形BDCF=×BC×DF=2,
∴四边形ACFB的面积=2+=3.
22.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作.
23.(Ⅰ)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE,
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(Ⅱ)解:结论:BE⊥AB.
由旋转的性质可知,∠ACD=∠BCE,
∵CA=CD,CB=CE,
∴∠CAD=∠CDA=∠CBE=∠CEB,
∵∠ABC+∠CAB+∠ACD+∠DCB=180°,
∴∠ABC+∠CBE+∠DCB+∠BCE=180°,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(Ⅲ)如图,设BC交DE于O.连接AO,过点B作BH⊥CD交CD的延长线于H,作BT⊥CE于T,
∵∠H=∠BTC=∠HCT=90°,
∴∠HBT=∠DBE=90°,
∴∠DBH=∠EBT,
∵BD=BE,∠H=∠BTE=90°
∴△BHD≌△BTE(AAS),
∴BH=BT,
∵BH⊥CH,BT⊥CE,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°.
24.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
25.解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠CAB=∠DAE=60°,
∵∠BFD=97°=∠AFE,
∴∠E=180°﹣97°﹣60°=23°,
∴∠ADC=∠E=23°;
(2)如图,连接DE,
∵AD=AE,∠DAE=60°,
∴△AED是等边三角形,
∴∠ADE=60°,AD=DE,
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE,
∴CD=BE=5,
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,
∴DE===4,
∴AD=DE=4.
26.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,AB=BC=AC,
∵又M是BC的中点,
∴∠AMB=∠AMN=90°,BC=2BM=2MC,∠BAM=∠BAC=30°,
∵AM顺时针旋转120°得到线段AB,
∴∠MAD=120°,AD=AM,
∴∠BAD=∠MAD﹣∠BAM=120°﹣30°=90°,
∴∠BAD=∠AMN=90°,
∵MC=CN,
∴MN=2MC=BC=AB,
在△DBA和△ANM中,
,
∴△DBA≌△ANM(SAS),
∴BD=AN.
(2)结论成立,理由如下:
①如图②﹣1中,当BM>BC时,分别过点A、点D作AG⊥BM、DH⊥BA垂足分别为G、H.
∴∠DHA=∠AGM=90°,
∵∠AMG+∠BAM+∠ABC=180°,∠ABC=160°,
∴∠AMG=180°﹣∠ABC﹣∠BAM=120°﹣∠BAM,
∵AM顺时针旋转120°得到线段AB,
∴∠MAD=120°,AD=AM,
∴∠DAB=120°﹣∠BAM,
∴∠DAB=∠AMB,
在△DAH和△AMG中,
,
∴△DAH≌△AMG(AAS),
∴DH=AG,AH=GM,
又∵△ABC是等边三角形,AG⊥BM,
∴BG=GC,
∴GN=GC+CN=GC+CM=BG+GC﹣GM=BC﹣GM,
又∵BH=AB﹣HA,AH=GM,AB=BC,
∴BH=GN.
∵DH=AG,∠DHA=∠AGM=90°,BH=GN,
在△DBH和△ANG中,
∴△DBH≌△ANG(SAS),
∴BD=AN.
②当BM<BC时,同法可得BD=AN.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
