2020-2021人教版八年级数学下册 18.2菱形同步练习题(含答案)
文档属性
| 名称 | 2020-2021人教版八年级数学下册 18.2菱形同步练习题(含答案) | 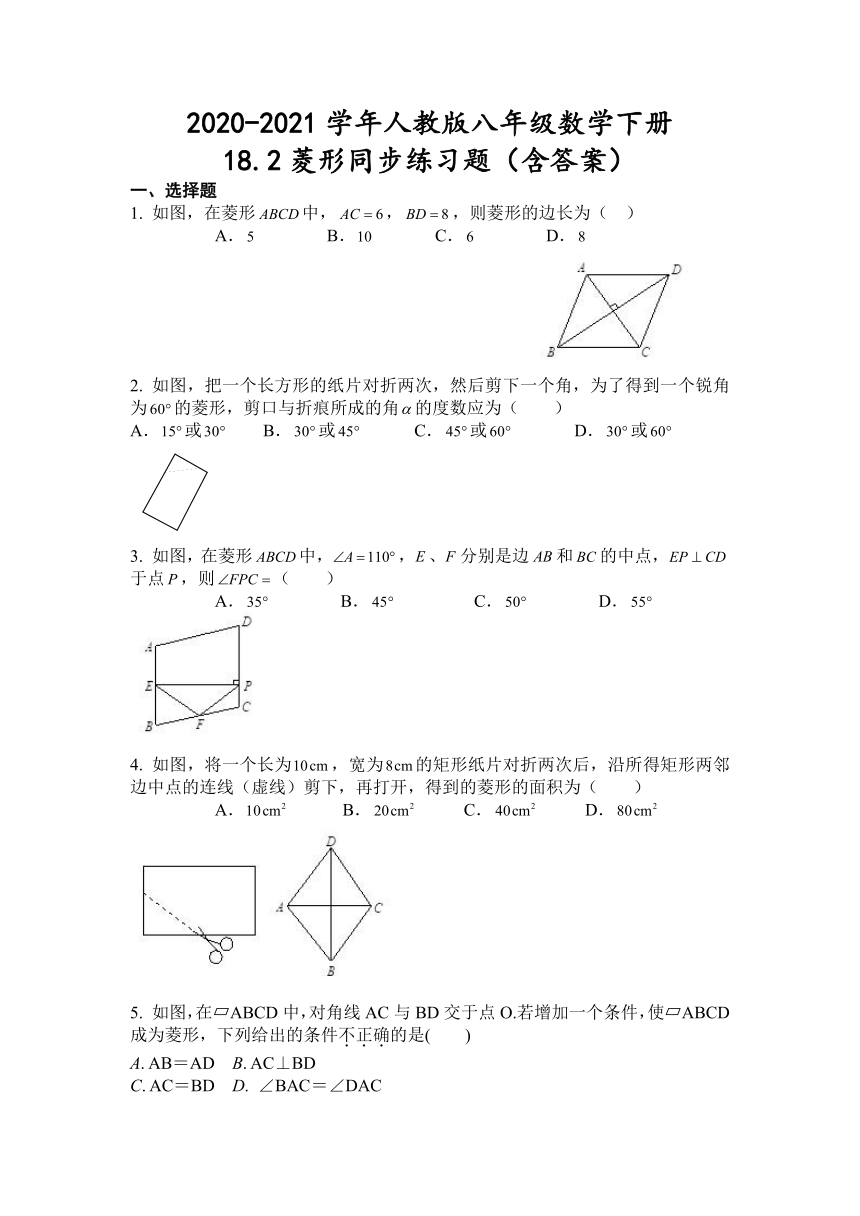 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 17:34:14 | ||
图片预览


文档简介
2020-2021学年人教版八年级数学下册
18.2菱形同步练习题(含答案)
一、选择题
1.
如图,在菱形中,,,则菱形的边长为(
)
A.
B.
C.
D.
2.
如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为的菱形,剪口与折痕所成的角的度数应为(
)
A.或
B.或
C.或
D.或
3.
如图,在菱形中,,、分别是边和的中点,于点,则(
)
A.
B.
C.
D.
4.
如图,将一个长为,宽为的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为(
)
A.
B.
C.
D.
5.
如图,在?ABCD中,对角线AC与BD交于点O.若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
A.
AB=AD
B.
AC⊥BD
C.
AC=BD
D.
∠BAC=∠DAC
6.
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
4
C.
6
D.
8
二、填空题
7.
菱形的两条对角线将菱形分成全等三角形的对数为
8.
如图所示,菱形中,对角线、相交于点,为边中点,菱形的周长为,则的长等于
.
9.
在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
10.
菱形中,、分别是、的中点,且,,那么等于
.
11.
如图,在菱形中,,、分别是、的中点,若,则菱形的边长是______.
三、解答题
12.
如图,是菱形的边的中点,于,交的延长线于,交于,
证明:与互相平分.
13.
如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
求证:四边形AODE是矩形.
14.
如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
15.
已知等腰中,,平分交于点,在线段上任取一点(点除外),过点作,分别交、于、点,作,交于点,连结.
⑴求证四边形为菱形
⑵当点在何处时,菱形的面积为四边形面积的一半?
参考答案
一、选择题
1.
【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2.
【答案】D
3.
【答案】D
4.
【答案】A
5.
【答案】C 【解析】邻边相等的平行四边形是菱形,所以A正确;对角线互相垂直的平行四边形是菱形,所以B正确;对角线相等的平行四边形是矩形,所以C错误;由∠BAC=∠DAC可得对角线是角平分线,所以D正确.
6.
【答案】A 【解析】∵E,F
分别是
AD,CD
边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
二、填空题
7.
【答案】
【解析】根据菱形的性质可知:共有对
8.
【答案】
9.
【答案】
【解析】根据菱形的性质可知:应当旋转至少
10.
【答案】
11.
【答案】
三、解答题
12.
【答案】连接、、
∵菱形中,,∴∥
∵∥,∴四边形是平行四边形,∴
∵,∴
又∵,∴四边形是平行四边形
∴与互相平分
13.
【答案】证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,(2分)
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,(4分)
∵四边形AODE是平行四边形,∠AOD=90°,
∴四边形AODE是矩形.(5分)
14.
【答案】(1)【思路分析】要证∠CEB=∠CBE,结合CE∥DB,可得到∠CEB=∠DBE,从而只需证明∠CBE=∠DBE,结合△ABC≌△ABD即可得证.
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD,
∵CE∥BD,
∴∠CEB=∠DBE,(2分)
∴∠CEB=∠CBE.(3分)
(2)证明:∵△ABC≌△ABD,∴BC=BD,
由(1)得∠CEB=∠CBE,
∴CE=CB,
∴CE=BD,(5分)
∵CE∥BD,
∴四边形BCED是平行四边形,(6分)
∵BC=BD,
∴四边形BCED是菱形.(8分)
15.
【答案】⑴∵
∴四边形为平行四边形
∵,平分
∴
∵
∴
∵
∴四边形为菱形
⑵当为中点时,
∵四边形为菱形,∴
∵
∴
又
∴四边形为平行四边形
E
F
D
B
C
A
18.2菱形同步练习题(含答案)
一、选择题
1.
如图,在菱形中,,,则菱形的边长为(
)
A.
B.
C.
D.
2.
如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为的菱形,剪口与折痕所成的角的度数应为(
)
A.或
B.或
C.或
D.或
3.
如图,在菱形中,,、分别是边和的中点,于点,则(
)
A.
B.
C.
D.
4.
如图,将一个长为,宽为的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为(
)
A.
B.
C.
D.
5.
如图,在?ABCD中,对角线AC与BD交于点O.若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
A.
AB=AD
B.
AC⊥BD
C.
AC=BD
D.
∠BAC=∠DAC
6.
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
4
C.
6
D.
8
二、填空题
7.
菱形的两条对角线将菱形分成全等三角形的对数为
8.
如图所示,菱形中,对角线、相交于点,为边中点,菱形的周长为,则的长等于
.
9.
在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
10.
菱形中,、分别是、的中点,且,,那么等于
.
11.
如图,在菱形中,,、分别是、的中点,若,则菱形的边长是______.
三、解答题
12.
如图,是菱形的边的中点,于,交的延长线于,交于,
证明:与互相平分.
13.
如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
求证:四边形AODE是矩形.
14.
如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
15.
已知等腰中,,平分交于点,在线段上任取一点(点除外),过点作,分别交、于、点,作,交于点,连结.
⑴求证四边形为菱形
⑵当点在何处时,菱形的面积为四边形面积的一半?
参考答案
一、选择题
1.
【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2.
【答案】D
3.
【答案】D
4.
【答案】A
5.
【答案】C 【解析】邻边相等的平行四边形是菱形,所以A正确;对角线互相垂直的平行四边形是菱形,所以B正确;对角线相等的平行四边形是矩形,所以C错误;由∠BAC=∠DAC可得对角线是角平分线,所以D正确.
6.
【答案】A 【解析】∵E,F
分别是
AD,CD
边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
二、填空题
7.
【答案】
【解析】根据菱形的性质可知:共有对
8.
【答案】
9.
【答案】
【解析】根据菱形的性质可知:应当旋转至少
10.
【答案】
11.
【答案】
三、解答题
12.
【答案】连接、、
∵菱形中,,∴∥
∵∥,∴四边形是平行四边形,∴
∵,∴
又∵,∴四边形是平行四边形
∴与互相平分
13.
【答案】证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,(2分)
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,(4分)
∵四边形AODE是平行四边形,∠AOD=90°,
∴四边形AODE是矩形.(5分)
14.
【答案】(1)【思路分析】要证∠CEB=∠CBE,结合CE∥DB,可得到∠CEB=∠DBE,从而只需证明∠CBE=∠DBE,结合△ABC≌△ABD即可得证.
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD,
∵CE∥BD,
∴∠CEB=∠DBE,(2分)
∴∠CEB=∠CBE.(3分)
(2)证明:∵△ABC≌△ABD,∴BC=BD,
由(1)得∠CEB=∠CBE,
∴CE=CB,
∴CE=BD,(5分)
∵CE∥BD,
∴四边形BCED是平行四边形,(6分)
∵BC=BD,
∴四边形BCED是菱形.(8分)
15.
【答案】⑴∵
∴四边形为平行四边形
∵,平分
∴
∵
∴
∵
∴四边形为菱形
⑵当为中点时,
∵四边形为菱形,∴
∵
∴
又
∴四边形为平行四边形
E
F
D
B
C
A
