第3章图形的平移与旋转 单元综合提升-2020-2021学年北师大版八年级数学下册同步提升训练(word版含解析)
文档属性
| 名称 | 第3章图形的平移与旋转 单元综合提升-2020-2021学年北师大版八年级数学下册同步提升训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 15:50:56 | ||
图片预览


文档简介
2021年北师大版八年级数学下册《第3章图形的平移与旋转》单元综合同步训练(附答案)
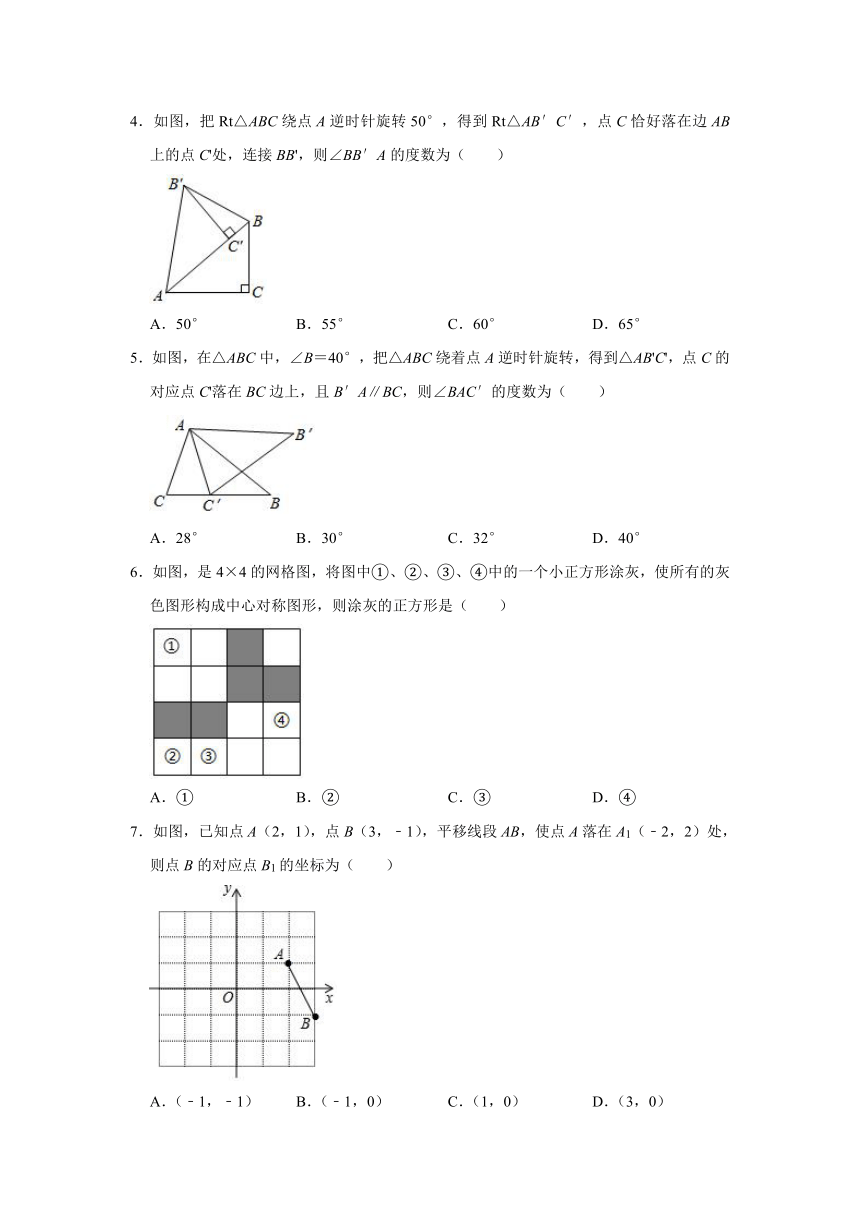
1.如图,将△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,点C的对应点F在BC的延长线上,连接AD.下列结论一定正确的是( )
A.∠B=∠F
B.AC⊥DE
C.BC=DF
D.AC平分DE
2.如图,在△ABC中,AB=5,BC=8,∠B=60°,将△ABC沿射线BC的方向平移,得到△A'B'C',再将△A'B'C'绕点A'逆时针旋转一定角度后,点B'恰好与点C重合,则平移的距离为( )
A.2
B.3
C.4
D.5
3.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B顺时针旋转60°,得到△BAE,连接ED,若BC=6,BD=5,则以下五个结论:
①△BDE是等边三角形;
②AE∥BC;
③△ADE的周长是11;
④∠ADE=∠BDC;
⑤∠AED=∠ABD.
其中正确的个数是( )
A.2个
B.3个
C.4个
D.5个
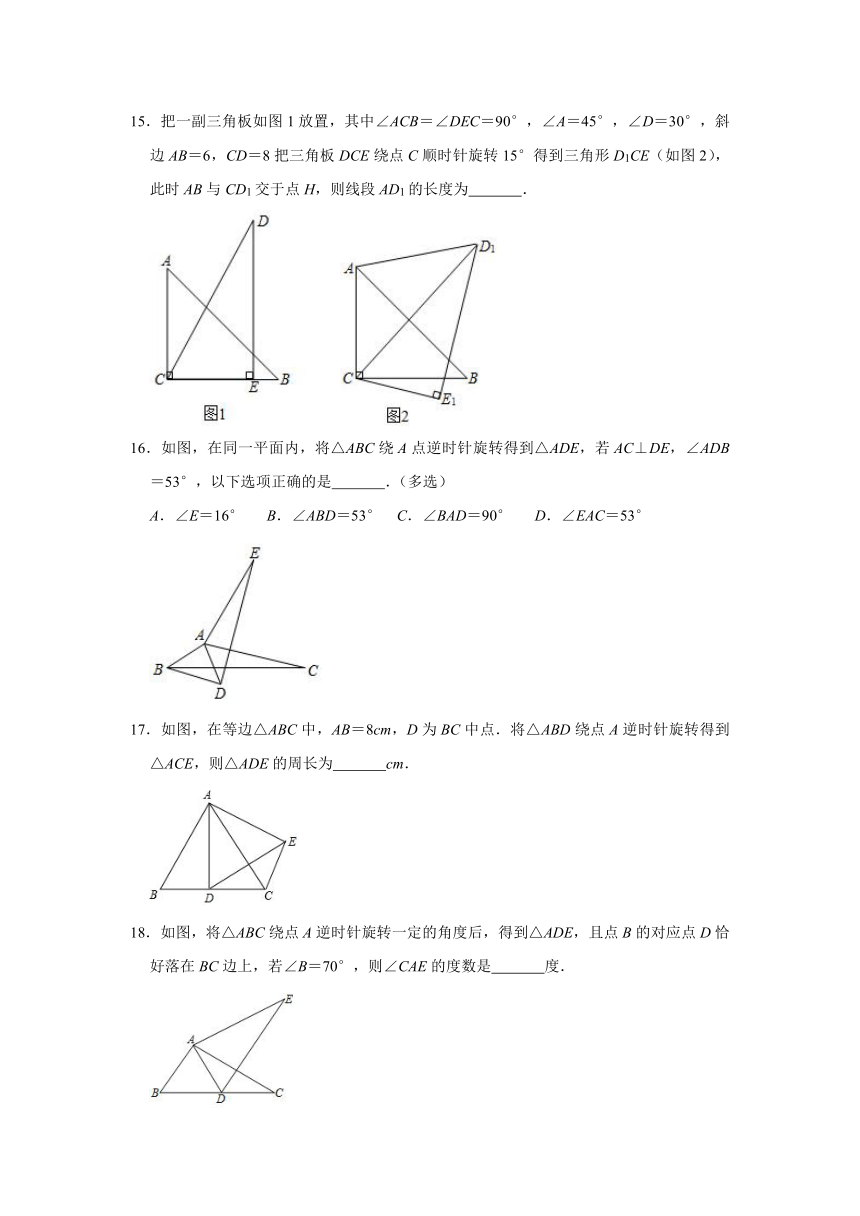
4.如图,把Rt△ABC绕点A逆时针旋转50°,得到Rt△AB′C′,点C恰好落在边AB上的点C'处,连接BB',则∠BB′A的度数为( )
A.50°
B.55°
C.60°
D.65°
5.如图,在△ABC中,∠B=40°,把△ABC绕着点A逆时针旋转,得到△AB'C',点C的对应点C'落在BC边上,且B′A∥BC,则∠BAC′的度数为( )
A.28°
B.30°
C.32°
D.40°
6.如图,是4×4的网格图,将图中①、②、③、④中的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的正方形是( )
A.①
B.②
C.③
D.④
7.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1)
B.(﹣1,0)
C.(1,0)
D.(3,0)
8.如图,把△ABC绕着点A顺时针方向旋转角度α(0°<α<90°),得到△AB'C',若B',C,C'三点在同一条直线上,∠B'CB=46°,则α的度数是
.
9.如图,将△ABC绕顶点A顺时针旋转60°后得到△AB1C1,且C1为BC的中点,AB与B1C1相交于D,若AC=2,则线段B1D的长度为
.
10.如图,在△ABC中,∠A=45°,∠ACB=75°,BC=5,将△ABC绕点C旋转得到△A'B'C,且点B'恰好落在AB边上,则BB'的长为
.
11.若点P(3m﹣1,2+m)关于原点的对称点P′在第四象限,则m的取值范围是
.
12.已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为
.
13.如图,在△ADE中,∠DAE=80°,将△ADE绕点A顺时针旋转α得△ABC,若AC平分∠DAE,则α=
;若AC平分∠BAE,则α=
.
14.如图,在直角三角形ABC中,∠ACB=90°,以直角顶点C为旋转中心,将三角形ABC逆时针旋转到△A'B'C'的位置,其中A'、B'分别是A、B的对应点,且∠ACD=2∠A′CB,则∠ACB′=
.
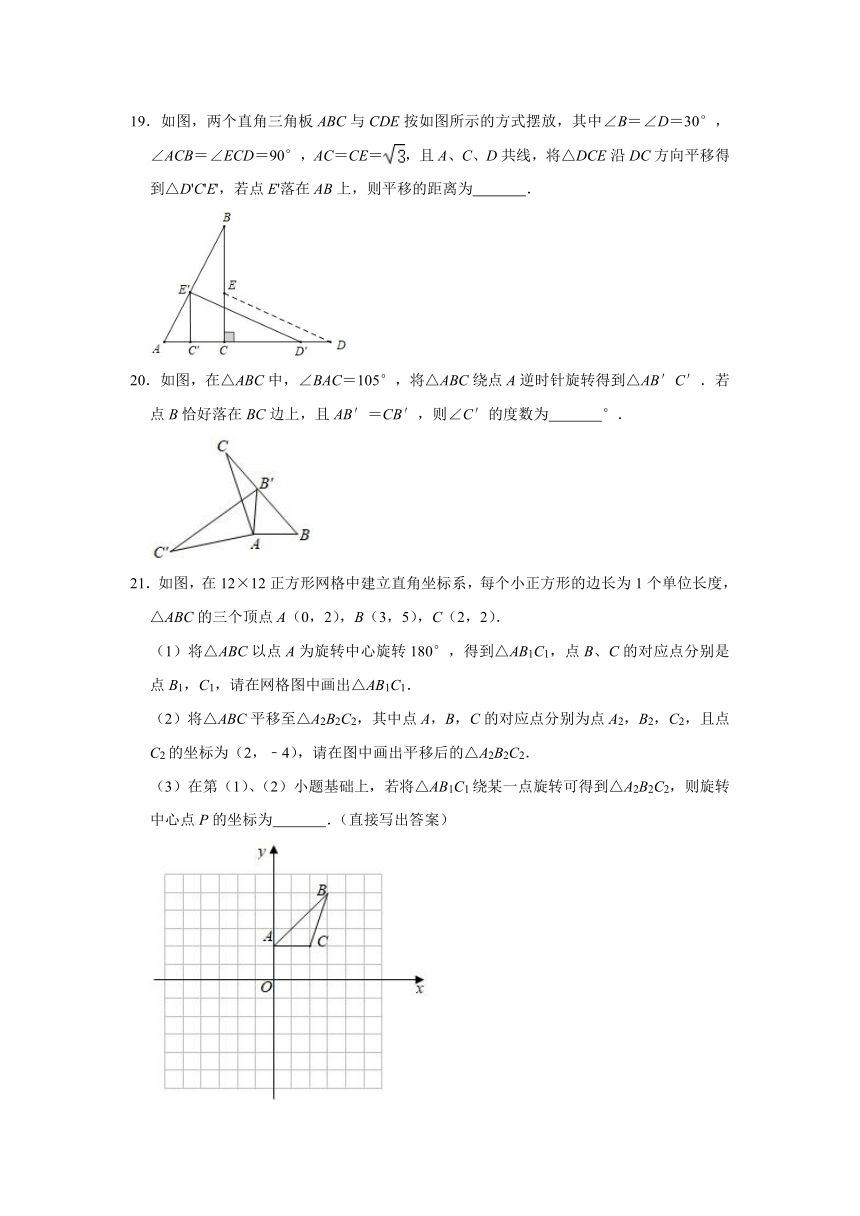
15.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,CD=8把三角板DCE绕点C顺时针旋转15°得到三角形D1CE(如图2),此时AB与CD1交于点H,则线段AD1的长度为
.
16.如图,在同一平面内,将△ABC绕A点逆时针旋转得到△ADE,若AC⊥DE,∠ADB=53°,以下选项正确的是
.(多选)
A.∠E=16°
B.∠ABD=53°
C.∠BAD=90°
D.∠EAC=53°
17.如图,在等边△ABC中,AB=8cm,D为BC中点.将△ABD绕点A逆时针旋转得到△ACE,则△ADE的周长为
cm.
18.如图,将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是
度.
19.如图,两个直角三角板ABC与CDE按如图所示的方式摆放,其中∠B=∠D=30°,∠ACB=∠ECD=90°,AC=CE=,且A、C、D共线,将△DCE沿DC方向平移得到△D'C'E',若点E'落在AB上,则平移的距离为
.
20.如图,在△ABC中,∠BAC=105°,将△ABC绕点A逆时针旋转得到△AB′C′.若点B恰好落在BC边上,且AB′=CB′,则∠C′的度数为
°.
21.如图,在12×12正方形网格中建立直角坐标系,每个小正方形的边长为1个单位长度,△ABC的三个顶点A(0,2),B(3,5),C(2,2).
(1)将△ABC以点A为旋转中心旋转180°,得到△AB1C1,点B、C的对应点分别是点B1,C1,请在网格图中画出△AB1C1.
(2)将△ABC平移至△A2B2C2,其中点A,B,C的对应点分别为点A2,B2,C2,且点C2的坐标为(2,﹣4),请在图中画出平移后的△A2B2C2.
(3)在第(1)、(2)小题基础上,若将△AB1C1绕某一点旋转可得到△A2B2C2,则旋转中心点P的坐标为
.(直接写出答案)
22.如图,在平面直角坐标系中,△ABC的三个顶点的坐标别为A(﹣2,4),B(﹣4,2),C(﹣1,0).
(1)将△ABC先向右平移3个单位,再向下平移4个单位,则得到△A1B1C1,请在图中画出△A1B1C1;
(2)请直接写点B1的坐标
;
(3)求出△ABC的面积.
23.在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,4),C(5,1).
(1)请在图1中画出△ABC关于坐标原点O成中心对称的图形△A1B1C1,并直接写出点C1的坐标;
(2)将△ABC绕着点C按逆时针方向旋转90°后得到△A2B2C2,请在图2中画出△A2B2C2,并直接写出点B2的坐标;
(3)将△ABC先向左平移5个单位长度,再向上平移1个单位长度,得到△A3B3C3.
①请在图3中画出△A3B3C3;
②若将△A3B3C3看成是由△ABC经过一次平移得到的,则这一平移的距离是
个单位长度.
24.已知△ABC的三个顶点位置分别是A(1,0),B(﹣3,0),C(x,y).
(1)若x=﹣2,y=3,求△ABC的面积;
(2)如图,若顶点C(x,y)位于第二象限,且CB∥y轴,AC与y轴相交于点E(0,1),当△ABC沿x正半轴方向平移,得到△DOF,且△DOF与原△ABC重叠部分为△AOE,求阴影部分的面积S;
(3)若点C到y轴的距离为4,点P(0,5),当S△ABC=2S△ABP,求点C的坐标.
25.将一副三角板如图①放置,点B、A、E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图①,∠ADE的度数为
,∠ABC的度数为
;
(2)若将三角板ADE绕点A逆时针旋转角α(0°<α<90°).
①如图②,当旋转角α等于45°时,试问DE∥BA吗?请说明理由;
②如图③,当AD⊥BC于点F时,请求出旋转角α的度数.
26.如图1,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
(1)求出∠ACE的度数;
(2)请在图1中找出一对全等的三角形,并说明全等的理由;
(3)若将△CDE绕C点转动到如图2所示的位置,其余条件不变,(2)中的结论是否还成立,试说明理由.
27.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为
;
(2)如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为
.
参考答案
1.解:∵△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,
∴∠B=∠DEF,BE=CF=CE=AD,AD∥BC,DF=AC,
只有当∠BAC=90°时,AC⊥DE;
只有当BC=2AC时,DF=AC=BE,所以A、B、C选项的结论不一定正确;
设AC交DE于O点,如图,
∵AD∥BC,
∴∠OAD=∠OCE,∠ODA=∠OEC,
而AD=CE,
∴△AOD≌△COE(ASA),
∴OD=OE,即AC平分DE,所以D选项的结论正确.
故选:D.
2.解:∵将△A'B'C'绕点A'逆时针旋转一定角度后,点B'恰好与点C重合,
∴B'C=A'C,
∵将△ABC沿射线BC的方向平移,得到△A'B'C',
∴AB=A'B'=5,∠B=∠A'B'C=60°,
∴△A'B'C是等边三角形,
∴A'B'=B'C=5,
∴BB'=3,
∴平移的距离为3,
故选:B.
3.解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=5,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+5=6+5=11,所以③正确.
∵∠EAB=∠EDB=60°,
∴∠AED=∠ABD.
故⑤正确.
故选:C.
4.解:∵Rt△ABC绕点A逆时针旋转50°得到Rt△AB′C′,
∴AB'=AB,∠BAB'=50°,∠ACB=∠AC'B'=90°
∴∠BB'A=∠ABB'=65°.
故选:D.
5.解:由旋转的性质得:∠B'=∠B=40°,∠AC'B'=∠C,AC'=AC,
∴∠AC'C=∠C=∠AC'B',
∵B'A∥BC,
∴∠B'+∠B'C'C=180°,
∴∠B'C'C=180°﹣40°=140°,
∴∠AC'C=∠C=∠AC'B'=×140°=70°,
∴∠BAC'=∠AC'C﹣∠B=70°﹣40°=30°;
故选:B.
6.解:根据中心对称的性质可知:
使所有的灰色图形构成中心对称图形,则涂灰的正方形是③.
故选:C.
7.解:观察图像可知,B1(﹣1,0).
故选:B.
8.解:由题意可得:AC=AC′,∠C'=∠ACB,
∴∠ACC'=∠C',
∵把△ABC绕着点A顺时针方向旋转α,得到△AB′C′,点C刚好落在边B′C′上,
∴∠B'CB+∠ACB=∠C'+∠CAC′,
∠B'CB=∠CAC'=46°.
故答案为:46°.
9.解:根据旋转的性质可知:AC=AC1,∠AC1B1=∠C=60°,
∵旋转角是60°,即∠C1AC=60°,
∴△ACC1为等边三角形,
∴BC1=CC1=AC=2,
∵C1为BC的中点,
∴BC1=AC1=2=AC1,
∴∠B=∠C1AB=30°,
∴∠BDC1=∠C1AB+∠AC1B1=90°,
∴BC1=2C1D,
∴C1D=1
∴BC=B1C1=BC1+CC1=4,
∴B1D=3,
故答案为:3.
10.解:∵△ABC中,∠A=45°,∠ACB=75°,
∴∠B=180°﹣45°﹣75°=60°,
由旋转的性质得:CB'=CB,
∴△BCB'是等边三角形,
∴BB'=BC=5;
故答案为:5.
11.解:∵点P(3m﹣1,2+m)关于原点的对称点P′(﹣3m+1,﹣2﹣m)在第四象限,
∴,
解得:﹣2<m<.
故答案为:﹣2<m<.
12.解:∵A(﹣1,0)平移后对应点A′的坐标为(1,﹣3),
∴A点的平移方法是:先向右平移2个单位,再向下平移3个单位,
∴B点的平移方法与A点的平移方法是相同的,
∴B(1,2)平移后B′的坐标是:(3,﹣1).
?故答案为(3,﹣1).
13.解:由旋转的性质得:∠BAC=∠DAE=80°,
∴∠1=∠2=α,
若AC平分∠DAE,
则α=∠2=∠DAE=40°;
若AC平分∠BAE,
则AC与AD重合,α=∠DAE=80°;
故答案为:40°;80°.
14.解:∵∠ACB=90°,∠ACD=2∠A′CB,
∴∠ACD=60°,∠A′CB=30°,
∵以直角顶点C为旋转中心,将三角形ABC逆时针旋转到△A'B'C'的位置,其中A'、B'分别是A、B的对应点,
∴∠BCB′=∠DCA=60°,
∴∠ACB′=∠ACB+∠BCB′=90°+60°=150°,
故答案为:150°.
15.解:如图,AB于CD1交于点H,
∵∠ACB=∠DEC=90°,∠BAC=45°,∠CDE=30°,斜边AB=6,CD=8,
∴AC=BC=3,∠DCE=60°,∠ABC=∠BAC=45°,
∵将三角板DCE绕点C顺时针旋转15°得到三角形D1CE,
∴∠D1CB=45°,CD1=CD=8,
∴AB⊥CD1,
∴AH=CH=3,
∴D1H=5,
∴AD1===,
故答案为:.
16.解:∵将△ABC绕A点逆时针旋转到△ADE的位置.
∴AB=AD,∠E=∠C,∠BAD=∠EAC,
∵AB=AD,
∴∠ABD=∠ADB=53°,故B选项正确;
∴∠BAD=180°﹣53°﹣53°=74°=∠EAC,故C选项错误,选项D错误;
∵AC⊥DE,
∴∠CAD+∠ADE=90°,
∵∠E=180°﹣∠EAC﹣∠CAD﹣∠EDA,
∴∠E=16°=∠ACB,故A选项正确,
正确选项的是A,B.
故答案为A,B.
17.解:∵△ABC是等边三角形,
∴AB=BC=AC=8cm,∠BAC=60°,
∵D为BC中点,
∵BD=DC=4cm,AD⊥BC,
∴AD===4(cm),
∵△ABD绕点A逆时针旋转后得到△ACE,
∴∠BAD=∠CAE,AD=AE,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴DE=AD=AE=4cm,
∴△ADE的周长为12cm,
故答案为:12.
18.解:∵将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,
∴AB=AD,∠BAD=∠CAE,
∴∠B=∠ADB=70°,
∴∠BAD=40°=∠CAE,
故答案为:40.
19.解:∵将△DCE沿DC方向平移得到△D'C'E',
∴C′E′=,
∵∠B=∠D=30°,∠ACB=∠ECD=90°,
∴∠E′C′A=90°,∠A=60°,
∴∠AE′C′=30°,
设AC′=x,则AE′=2x,
∵AE′2=AC′2+C′E′2,
∴(2x)2=x2+()2,
∴x=1,
∴平移的距离CC′=AC﹣AC′=﹣1,
故答案为:﹣1.
20.解:∵∠BAC=105°,
∴∠B+∠C=75°,
∵AB′=CB′,
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A逆时针旋转得到△AB′C′,
∴AB=AB',
∴∠B=∠AB'B=2∠C,
∴∠C=25°,
故答案为:25.
21.解:(1)如图,△AB1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)旋转中心点P的坐标为(0,﹣1).
故答案为:(0,﹣1).
22.解:(1)如图,△A1B1C1为所作;
(2)点B1的坐标为(﹣1,﹣2);
(3)△ABC的面积=3×4﹣×2×3﹣×1×4﹣×2×2=5.
故答案为(﹣1,﹣2).
23.解:(1)如图,△A1B1C1为所作,点C1的坐标为(﹣5,﹣1);
(2)如图,△A2B2C2为所作,点B2的坐标为(2,0);
(3)①如图,△A3B3C3为所作;
②BB3==,
所以平移的距离是个单位长度.
故答案为.
24.解:(1)∵A
(1,0),B(﹣3,0),C(﹣2,3),
∴△ABC的面积=×4×3=6;
(2)由题意得,∵E(0,1),
∴OE=OA=1,
∴△AOE是等腰直角三角形,
∵CB∥y轴,
∴△ABC是等腰直角三角形,
∴BC=AB=4,
∴y=4,
S阴影=S梯形BOEC=(4+1)=×4+=;
(3)由题意得,2S△ABP=2×=20,
当C在y轴的左侧时,设C(﹣4,y),
S△ABC=4×|y|=20,
解得:y=±10,
此时,C(﹣4,10)或C(﹣4,﹣10);
当C在y轴的右侧时,设C(4,y),
S△ABC=4×|y|=20,
解得:y=±10,
此时,C(4,10)或C(4,﹣10);
综上所述,C(﹣4,10)或C(﹣4,﹣10)或C(4,10)或C(4,﹣10).
25.解:(1)∠ADE的度数为45°,∠ABC的度数为60°,
故答案为:45°,60°;
(2)①当旋转角α等于45°时,
∴∠BAC=90°,
又∠α=45°,
∴∠BAD=∠BAC﹣∠α=45°,
又∠ADE=45°
∴∠BAD=∠ADE,
∴DE∥BA;
②当AD⊥BC于点F时,
∴∠AFC=90°,
∵∠C=30°,
∴∠α=180°﹣∠AFC﹣∠C=180°﹣90°﹣30°=60°.
26.解:(1)∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,
∵点B、C、D在同一条直线上,
∴∠ACE=180°﹣∠ACB﹣∠ECD=180°﹣60°﹣60°=60°;
(2)△BCE≌△ACD.
理由:∵△ABC和△CED都是等边三角形,
∠BCA=∠DCE=60°,BC=AC,CE=CD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS);
(3)(2)中的结论还成立.
∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,AC=BC,EC=DC.
∴∠BCE=∠ACD,
∴△BCE≌△ACD(SAS).
27.解:(1)将小路往左平移,直到E、F与A、B重合,则平移后的四边形EFF1E1是一个矩形,并且EF=AB=30,FF1=EE1=1,
则草地的面积为:50×30﹣1×30=1470(平方米);
故答案为:1470平方米;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(50﹣1)×(30﹣1)=1421(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30﹣1+50+30﹣1=108(米).
故答案为:108米
1.如图,将△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,点C的对应点F在BC的延长线上,连接AD.下列结论一定正确的是( )
A.∠B=∠F
B.AC⊥DE
C.BC=DF
D.AC平分DE
2.如图,在△ABC中,AB=5,BC=8,∠B=60°,将△ABC沿射线BC的方向平移,得到△A'B'C',再将△A'B'C'绕点A'逆时针旋转一定角度后,点B'恰好与点C重合,则平移的距离为( )
A.2
B.3
C.4
D.5
3.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B顺时针旋转60°,得到△BAE,连接ED,若BC=6,BD=5,则以下五个结论:
①△BDE是等边三角形;
②AE∥BC;
③△ADE的周长是11;
④∠ADE=∠BDC;
⑤∠AED=∠ABD.
其中正确的个数是( )
A.2个
B.3个
C.4个
D.5个
4.如图,把Rt△ABC绕点A逆时针旋转50°,得到Rt△AB′C′,点C恰好落在边AB上的点C'处,连接BB',则∠BB′A的度数为( )
A.50°
B.55°
C.60°
D.65°
5.如图,在△ABC中,∠B=40°,把△ABC绕着点A逆时针旋转,得到△AB'C',点C的对应点C'落在BC边上,且B′A∥BC,则∠BAC′的度数为( )
A.28°
B.30°
C.32°
D.40°
6.如图,是4×4的网格图,将图中①、②、③、④中的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的正方形是( )
A.①
B.②
C.③
D.④
7.如图,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1)
B.(﹣1,0)
C.(1,0)
D.(3,0)
8.如图,把△ABC绕着点A顺时针方向旋转角度α(0°<α<90°),得到△AB'C',若B',C,C'三点在同一条直线上,∠B'CB=46°,则α的度数是
.
9.如图,将△ABC绕顶点A顺时针旋转60°后得到△AB1C1,且C1为BC的中点,AB与B1C1相交于D,若AC=2,则线段B1D的长度为
.
10.如图,在△ABC中,∠A=45°,∠ACB=75°,BC=5,将△ABC绕点C旋转得到△A'B'C,且点B'恰好落在AB边上,则BB'的长为
.
11.若点P(3m﹣1,2+m)关于原点的对称点P′在第四象限,则m的取值范围是
.
12.已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为
.
13.如图,在△ADE中,∠DAE=80°,将△ADE绕点A顺时针旋转α得△ABC,若AC平分∠DAE,则α=
;若AC平分∠BAE,则α=
.
14.如图,在直角三角形ABC中,∠ACB=90°,以直角顶点C为旋转中心,将三角形ABC逆时针旋转到△A'B'C'的位置,其中A'、B'分别是A、B的对应点,且∠ACD=2∠A′CB,则∠ACB′=
.
15.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,CD=8把三角板DCE绕点C顺时针旋转15°得到三角形D1CE(如图2),此时AB与CD1交于点H,则线段AD1的长度为
.
16.如图,在同一平面内,将△ABC绕A点逆时针旋转得到△ADE,若AC⊥DE,∠ADB=53°,以下选项正确的是
.(多选)
A.∠E=16°
B.∠ABD=53°
C.∠BAD=90°
D.∠EAC=53°
17.如图,在等边△ABC中,AB=8cm,D为BC中点.将△ABD绕点A逆时针旋转得到△ACE,则△ADE的周长为
cm.
18.如图,将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是
度.
19.如图,两个直角三角板ABC与CDE按如图所示的方式摆放,其中∠B=∠D=30°,∠ACB=∠ECD=90°,AC=CE=,且A、C、D共线,将△DCE沿DC方向平移得到△D'C'E',若点E'落在AB上,则平移的距离为
.
20.如图,在△ABC中,∠BAC=105°,将△ABC绕点A逆时针旋转得到△AB′C′.若点B恰好落在BC边上,且AB′=CB′,则∠C′的度数为
°.
21.如图,在12×12正方形网格中建立直角坐标系,每个小正方形的边长为1个单位长度,△ABC的三个顶点A(0,2),B(3,5),C(2,2).
(1)将△ABC以点A为旋转中心旋转180°,得到△AB1C1,点B、C的对应点分别是点B1,C1,请在网格图中画出△AB1C1.
(2)将△ABC平移至△A2B2C2,其中点A,B,C的对应点分别为点A2,B2,C2,且点C2的坐标为(2,﹣4),请在图中画出平移后的△A2B2C2.
(3)在第(1)、(2)小题基础上,若将△AB1C1绕某一点旋转可得到△A2B2C2,则旋转中心点P的坐标为
.(直接写出答案)
22.如图,在平面直角坐标系中,△ABC的三个顶点的坐标别为A(﹣2,4),B(﹣4,2),C(﹣1,0).
(1)将△ABC先向右平移3个单位,再向下平移4个单位,则得到△A1B1C1,请在图中画出△A1B1C1;
(2)请直接写点B1的坐标
;
(3)求出△ABC的面积.
23.在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,4),C(5,1).
(1)请在图1中画出△ABC关于坐标原点O成中心对称的图形△A1B1C1,并直接写出点C1的坐标;
(2)将△ABC绕着点C按逆时针方向旋转90°后得到△A2B2C2,请在图2中画出△A2B2C2,并直接写出点B2的坐标;
(3)将△ABC先向左平移5个单位长度,再向上平移1个单位长度,得到△A3B3C3.
①请在图3中画出△A3B3C3;
②若将△A3B3C3看成是由△ABC经过一次平移得到的,则这一平移的距离是
个单位长度.
24.已知△ABC的三个顶点位置分别是A(1,0),B(﹣3,0),C(x,y).
(1)若x=﹣2,y=3,求△ABC的面积;
(2)如图,若顶点C(x,y)位于第二象限,且CB∥y轴,AC与y轴相交于点E(0,1),当△ABC沿x正半轴方向平移,得到△DOF,且△DOF与原△ABC重叠部分为△AOE,求阴影部分的面积S;
(3)若点C到y轴的距离为4,点P(0,5),当S△ABC=2S△ABP,求点C的坐标.
25.将一副三角板如图①放置,点B、A、E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图①,∠ADE的度数为
,∠ABC的度数为
;
(2)若将三角板ADE绕点A逆时针旋转角α(0°<α<90°).
①如图②,当旋转角α等于45°时,试问DE∥BA吗?请说明理由;
②如图③,当AD⊥BC于点F时,请求出旋转角α的度数.
26.如图1,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
(1)求出∠ACE的度数;
(2)请在图1中找出一对全等的三角形,并说明全等的理由;
(3)若将△CDE绕C点转动到如图2所示的位置,其余条件不变,(2)中的结论是否还成立,试说明理由.
27.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为
;
(2)如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为
.
参考答案
1.解:∵△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,
∴∠B=∠DEF,BE=CF=CE=AD,AD∥BC,DF=AC,
只有当∠BAC=90°时,AC⊥DE;
只有当BC=2AC时,DF=AC=BE,所以A、B、C选项的结论不一定正确;
设AC交DE于O点,如图,
∵AD∥BC,
∴∠OAD=∠OCE,∠ODA=∠OEC,
而AD=CE,
∴△AOD≌△COE(ASA),
∴OD=OE,即AC平分DE,所以D选项的结论正确.
故选:D.
2.解:∵将△A'B'C'绕点A'逆时针旋转一定角度后,点B'恰好与点C重合,
∴B'C=A'C,
∵将△ABC沿射线BC的方向平移,得到△A'B'C',
∴AB=A'B'=5,∠B=∠A'B'C=60°,
∴△A'B'C是等边三角形,
∴A'B'=B'C=5,
∴BB'=3,
∴平移的距离为3,
故选:B.
3.解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=5,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+5=6+5=11,所以③正确.
∵∠EAB=∠EDB=60°,
∴∠AED=∠ABD.
故⑤正确.
故选:C.
4.解:∵Rt△ABC绕点A逆时针旋转50°得到Rt△AB′C′,
∴AB'=AB,∠BAB'=50°,∠ACB=∠AC'B'=90°
∴∠BB'A=∠ABB'=65°.
故选:D.
5.解:由旋转的性质得:∠B'=∠B=40°,∠AC'B'=∠C,AC'=AC,
∴∠AC'C=∠C=∠AC'B',
∵B'A∥BC,
∴∠B'+∠B'C'C=180°,
∴∠B'C'C=180°﹣40°=140°,
∴∠AC'C=∠C=∠AC'B'=×140°=70°,
∴∠BAC'=∠AC'C﹣∠B=70°﹣40°=30°;
故选:B.
6.解:根据中心对称的性质可知:
使所有的灰色图形构成中心对称图形,则涂灰的正方形是③.
故选:C.
7.解:观察图像可知,B1(﹣1,0).
故选:B.
8.解:由题意可得:AC=AC′,∠C'=∠ACB,
∴∠ACC'=∠C',
∵把△ABC绕着点A顺时针方向旋转α,得到△AB′C′,点C刚好落在边B′C′上,
∴∠B'CB+∠ACB=∠C'+∠CAC′,
∠B'CB=∠CAC'=46°.
故答案为:46°.
9.解:根据旋转的性质可知:AC=AC1,∠AC1B1=∠C=60°,
∵旋转角是60°,即∠C1AC=60°,
∴△ACC1为等边三角形,
∴BC1=CC1=AC=2,
∵C1为BC的中点,
∴BC1=AC1=2=AC1,
∴∠B=∠C1AB=30°,
∴∠BDC1=∠C1AB+∠AC1B1=90°,
∴BC1=2C1D,
∴C1D=1
∴BC=B1C1=BC1+CC1=4,
∴B1D=3,
故答案为:3.
10.解:∵△ABC中,∠A=45°,∠ACB=75°,
∴∠B=180°﹣45°﹣75°=60°,
由旋转的性质得:CB'=CB,
∴△BCB'是等边三角形,
∴BB'=BC=5;
故答案为:5.
11.解:∵点P(3m﹣1,2+m)关于原点的对称点P′(﹣3m+1,﹣2﹣m)在第四象限,
∴,
解得:﹣2<m<.
故答案为:﹣2<m<.
12.解:∵A(﹣1,0)平移后对应点A′的坐标为(1,﹣3),
∴A点的平移方法是:先向右平移2个单位,再向下平移3个单位,
∴B点的平移方法与A点的平移方法是相同的,
∴B(1,2)平移后B′的坐标是:(3,﹣1).
?故答案为(3,﹣1).
13.解:由旋转的性质得:∠BAC=∠DAE=80°,
∴∠1=∠2=α,
若AC平分∠DAE,
则α=∠2=∠DAE=40°;
若AC平分∠BAE,
则AC与AD重合,α=∠DAE=80°;
故答案为:40°;80°.
14.解:∵∠ACB=90°,∠ACD=2∠A′CB,
∴∠ACD=60°,∠A′CB=30°,
∵以直角顶点C为旋转中心,将三角形ABC逆时针旋转到△A'B'C'的位置,其中A'、B'分别是A、B的对应点,
∴∠BCB′=∠DCA=60°,
∴∠ACB′=∠ACB+∠BCB′=90°+60°=150°,
故答案为:150°.
15.解:如图,AB于CD1交于点H,
∵∠ACB=∠DEC=90°,∠BAC=45°,∠CDE=30°,斜边AB=6,CD=8,
∴AC=BC=3,∠DCE=60°,∠ABC=∠BAC=45°,
∵将三角板DCE绕点C顺时针旋转15°得到三角形D1CE,
∴∠D1CB=45°,CD1=CD=8,
∴AB⊥CD1,
∴AH=CH=3,
∴D1H=5,
∴AD1===,
故答案为:.
16.解:∵将△ABC绕A点逆时针旋转到△ADE的位置.
∴AB=AD,∠E=∠C,∠BAD=∠EAC,
∵AB=AD,
∴∠ABD=∠ADB=53°,故B选项正确;
∴∠BAD=180°﹣53°﹣53°=74°=∠EAC,故C选项错误,选项D错误;
∵AC⊥DE,
∴∠CAD+∠ADE=90°,
∵∠E=180°﹣∠EAC﹣∠CAD﹣∠EDA,
∴∠E=16°=∠ACB,故A选项正确,
正确选项的是A,B.
故答案为A,B.
17.解:∵△ABC是等边三角形,
∴AB=BC=AC=8cm,∠BAC=60°,
∵D为BC中点,
∵BD=DC=4cm,AD⊥BC,
∴AD===4(cm),
∵△ABD绕点A逆时针旋转后得到△ACE,
∴∠BAD=∠CAE,AD=AE,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴DE=AD=AE=4cm,
∴△ADE的周长为12cm,
故答案为:12.
18.解:∵将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,
∴AB=AD,∠BAD=∠CAE,
∴∠B=∠ADB=70°,
∴∠BAD=40°=∠CAE,
故答案为:40.
19.解:∵将△DCE沿DC方向平移得到△D'C'E',
∴C′E′=,
∵∠B=∠D=30°,∠ACB=∠ECD=90°,
∴∠E′C′A=90°,∠A=60°,
∴∠AE′C′=30°,
设AC′=x,则AE′=2x,
∵AE′2=AC′2+C′E′2,
∴(2x)2=x2+()2,
∴x=1,
∴平移的距离CC′=AC﹣AC′=﹣1,
故答案为:﹣1.
20.解:∵∠BAC=105°,
∴∠B+∠C=75°,
∵AB′=CB′,
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A逆时针旋转得到△AB′C′,
∴AB=AB',
∴∠B=∠AB'B=2∠C,
∴∠C=25°,
故答案为:25.
21.解:(1)如图,△AB1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)旋转中心点P的坐标为(0,﹣1).
故答案为:(0,﹣1).
22.解:(1)如图,△A1B1C1为所作;
(2)点B1的坐标为(﹣1,﹣2);
(3)△ABC的面积=3×4﹣×2×3﹣×1×4﹣×2×2=5.
故答案为(﹣1,﹣2).
23.解:(1)如图,△A1B1C1为所作,点C1的坐标为(﹣5,﹣1);
(2)如图,△A2B2C2为所作,点B2的坐标为(2,0);
(3)①如图,△A3B3C3为所作;
②BB3==,
所以平移的距离是个单位长度.
故答案为.
24.解:(1)∵A
(1,0),B(﹣3,0),C(﹣2,3),
∴△ABC的面积=×4×3=6;
(2)由题意得,∵E(0,1),
∴OE=OA=1,
∴△AOE是等腰直角三角形,
∵CB∥y轴,
∴△ABC是等腰直角三角形,
∴BC=AB=4,
∴y=4,
S阴影=S梯形BOEC=(4+1)=×4+=;
(3)由题意得,2S△ABP=2×=20,
当C在y轴的左侧时,设C(﹣4,y),
S△ABC=4×|y|=20,
解得:y=±10,
此时,C(﹣4,10)或C(﹣4,﹣10);
当C在y轴的右侧时,设C(4,y),
S△ABC=4×|y|=20,
解得:y=±10,
此时,C(4,10)或C(4,﹣10);
综上所述,C(﹣4,10)或C(﹣4,﹣10)或C(4,10)或C(4,﹣10).
25.解:(1)∠ADE的度数为45°,∠ABC的度数为60°,
故答案为:45°,60°;
(2)①当旋转角α等于45°时,
∴∠BAC=90°,
又∠α=45°,
∴∠BAD=∠BAC﹣∠α=45°,
又∠ADE=45°
∴∠BAD=∠ADE,
∴DE∥BA;
②当AD⊥BC于点F时,
∴∠AFC=90°,
∵∠C=30°,
∴∠α=180°﹣∠AFC﹣∠C=180°﹣90°﹣30°=60°.
26.解:(1)∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,
∵点B、C、D在同一条直线上,
∴∠ACE=180°﹣∠ACB﹣∠ECD=180°﹣60°﹣60°=60°;
(2)△BCE≌△ACD.
理由:∵△ABC和△CED都是等边三角形,
∠BCA=∠DCE=60°,BC=AC,CE=CD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS);
(3)(2)中的结论还成立.
∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠ECD=60°,AC=BC,EC=DC.
∴∠BCE=∠ACD,
∴△BCE≌△ACD(SAS).
27.解:(1)将小路往左平移,直到E、F与A、B重合,则平移后的四边形EFF1E1是一个矩形,并且EF=AB=30,FF1=EE1=1,
则草地的面积为:50×30﹣1×30=1470(平方米);
故答案为:1470平方米;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(50﹣1)×(30﹣1)=1421(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30﹣1+50+30﹣1=108(米).
故答案为:108米
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
