8.5.1直线与直线平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共24张PPT)
文档属性
| 名称 | 8.5.1直线与直线平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 22:32:48 | ||
图片预览


文档简介
(共24张PPT)
8.5.1直线与直线平行
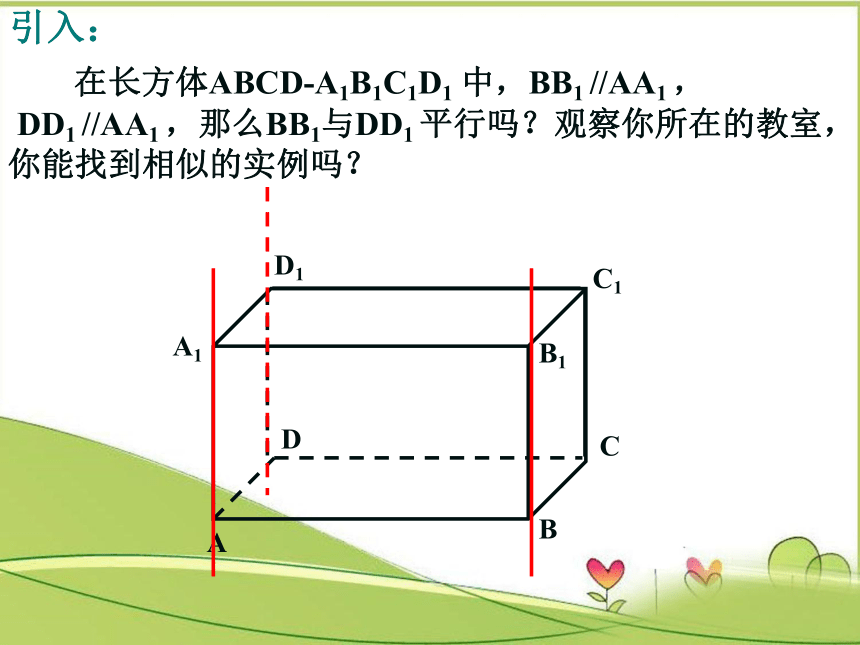
在长方体ABCD-A1B1C1D1
中,BB1
//AA1
,
DD1
//AA1
,那么BB1与DD1
平行吗?观察你所在的教室,
你能找到相似的实例吗?
A1
B1
C1
D1
A
B
C
D
引入:
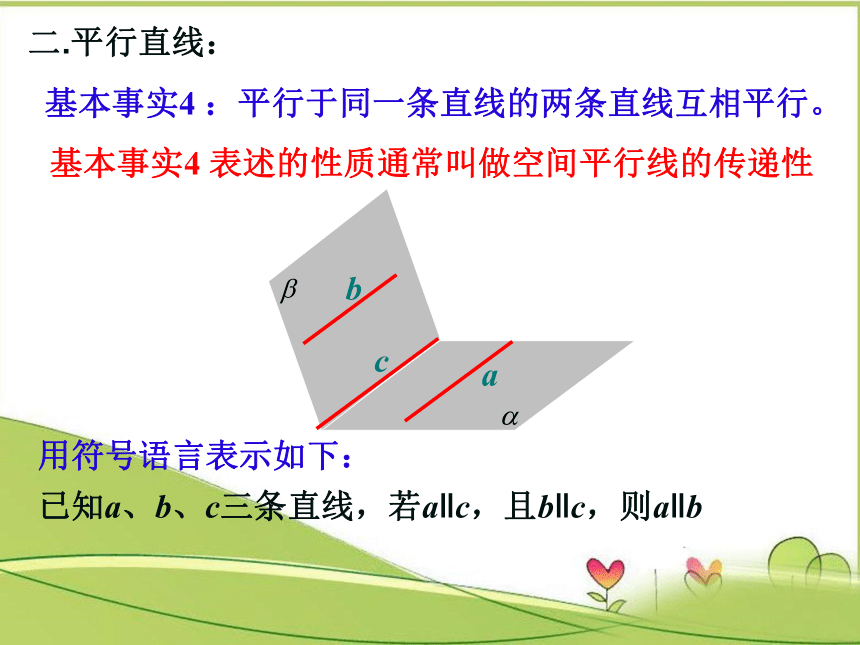
二.平行直线:
基本事实4
:平行于同一条直线的两条直线互相平行。
用符号语言表示如下:
已知a、b、c三条直线,若a‖c,且b‖c,则a‖b
a
b
c
基本事实4
表述的性质通常叫做空间平行线的传递性
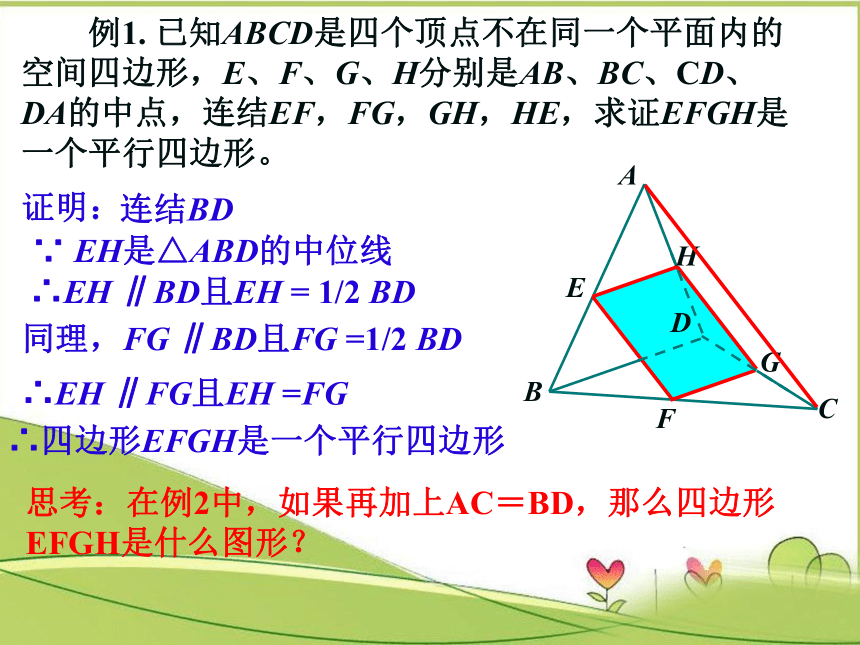
例1.
已知ABCD是四个顶点不在同一个平面内的空间四边形,E、F、G、H分别是AB、BC、CD、DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。
A
B
C
D
E
F
G
H
∵
EH是△ABD的中位线
∴EH
∥BD且EH
=
1/2
BD
同理,FG
∥BD且FG
=1/2
BD
∴EH
∥FG且EH
=FG
∴四边形EFGH是一个平行四边形
证明:
连结BD
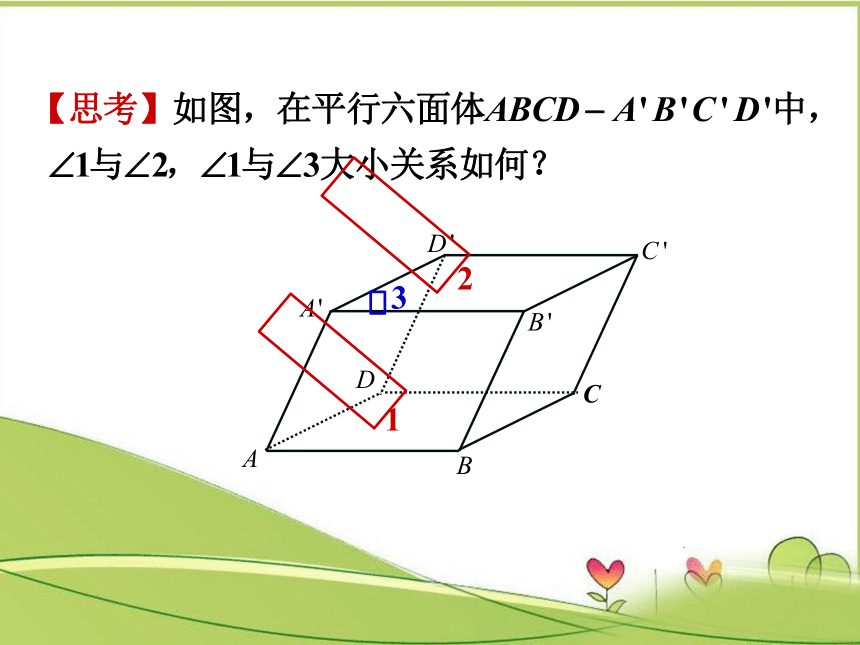
思考:在例2中,如果再加上AC=BD,那么四边形EFGH是什么图形?
2
1
3
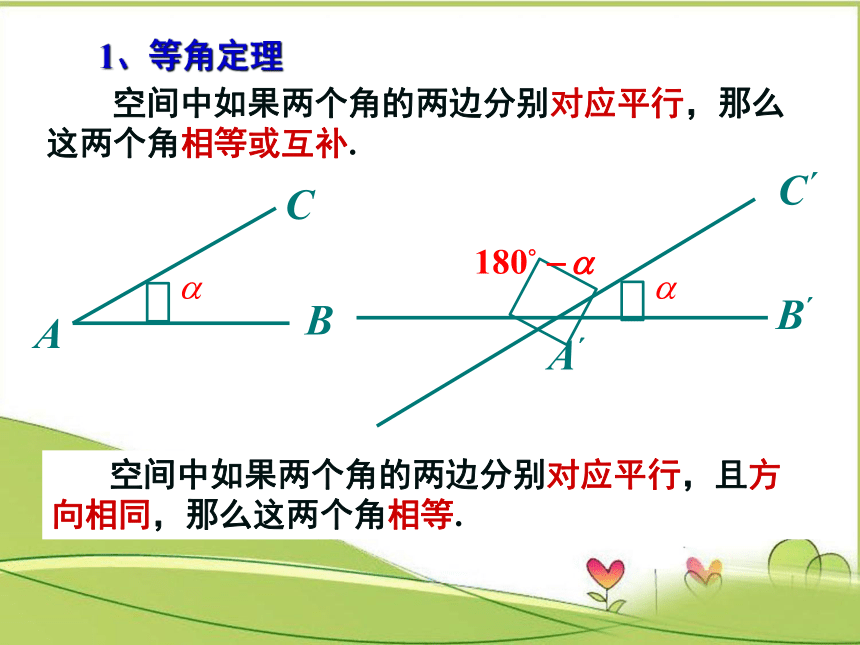
1、等角定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
B
C
A
B?
C?
A?
空间中如果两个角的两边分别对应平行,且方向相同,那么这两个角相等.
2、
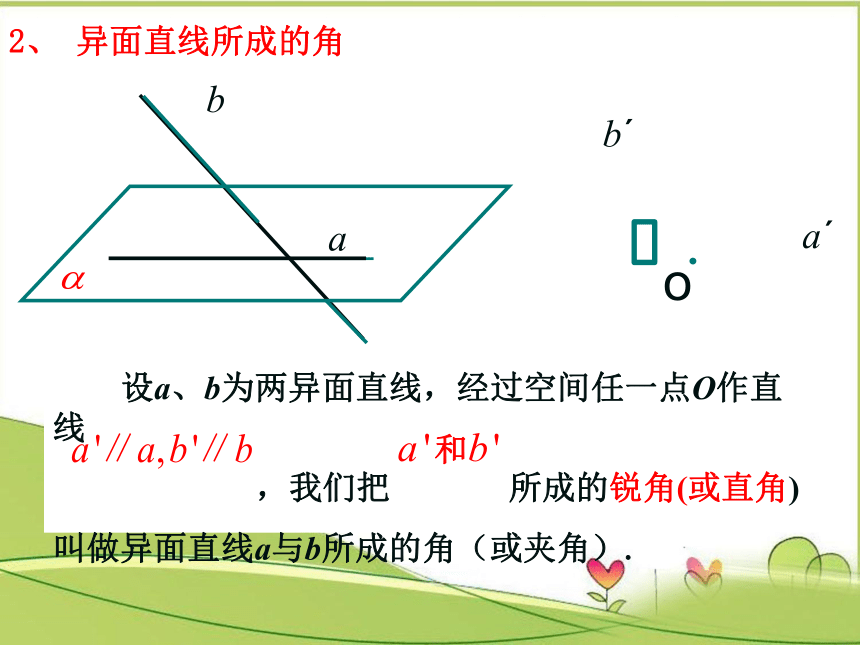
异面直线所成的角
a
b
o
aˊ
bˊ
设a、b为两异面直线,经过空间任一点O作直线
,我们把
所成的锐角(或直角)
叫做异面直线a与b所成的角(或夹角).
a
b
a
'
b'
o
a
'
b
'
o
'
a
O
b
a
'
3、两异面直线的夹角的取值范围:
若两条异面直线a、b的夹角为90?,则称这两条异面直线互相垂直,仍记作a⊥b
。
A
D
C
B
A1
B1
C1
D1
【思考1】在正方体
ABCD
-A1B1C1D1中,哪些棱所在直线与直线AA1垂直?
直线AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1分别与直线AA1垂直。
3、两异面直线的夹角的取值范围:
若两条异面直线a、b的夹角为90?,则称这两条异面直线互相垂直,仍记作a⊥b
。
【思考2】在平面内,垂直于同一条直线的两直线的位置关系如何?
在空间呢?
A
D
C
B
A1
B1
C1
D1
考点一、求异面直线的夹角
【例2】在正方体
ABCD
-A1B1C1D1中,
求直线A1B与C1C
的夹角。
解:∵BB1
‖CC1
,且∠A1BB1是锐角,
∴∠A1BB1是异面直线A1B与C1C
的夹角
∵∠A1BB1
=45°
∴异面直线A1B与C1C
的夹角为45°
方法小结:
求异面直线的夹角,关键是找到“相等的平面角”,将空间问题,转化为平面问题
二证
一作
三计算
作出或找出两异面直线所成的平面角,做平行线;
利用定义证明作出或找出的角是两异面直线所成的角;
把作出的角放在三角形中,解三角形
平移直线得出的角有可能是两条异面直线所成角的补角
(1)AD,
DC,
CC1,
B1C1,
DD1,
D1C1
(2)因为BB1
‖CC1
,
且∠A1BB1是
锐角,
所以∠A1BB1是异面直线A1B与
C1C
的夹角
因为∠A1BB1
=45°
所以异面直线A1B与C1C
的夹角为45°
例3、在正方体
ABCD
-A1B1C1D1中,
(1)哪些棱所在直线与直线A1B是异面直线?
(2)求直线A1B与C1C
的夹角;
(3)哪些棱所在直线与直线AA1垂直?
A
D
C
B
A1
B1
C1
D1
解:
(3)直线AB,
BC,
CD,
DA,
A1B1,
B1C1’
C1D1,
D1A1
分别与直线AA1垂直.
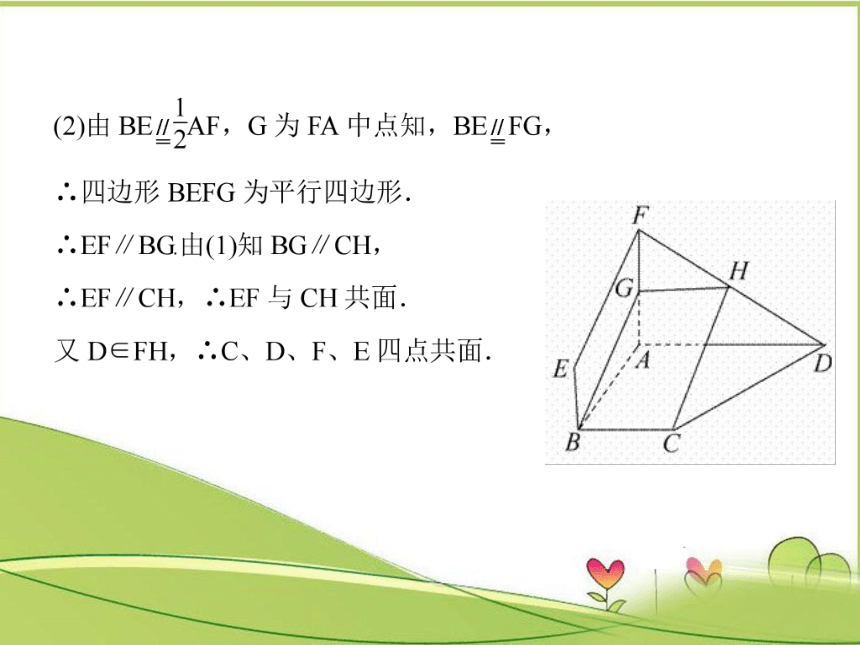
G
分析:
求异面直线的夹角,关键是找到
“相等的平面角”
由此可选取BD的中点G,连结GE,GF,
则异面直线EF和AB的夹角就是∠1或其补角
1
求异面直线的夹角
解:取BD的中点G,连结GE,GF,
∴∠1或其补角就是EF和AB所成角
G
1
求异面直线的夹角
A
B
C
F
E
G
D
A
C
B
A1
B1
C1
小结:
1.掌握等角定理
2.理解并会求异面直线所成的角
二证
一作
三计算
8.5.1直线与直线平行
在长方体ABCD-A1B1C1D1
中,BB1
//AA1
,
DD1
//AA1
,那么BB1与DD1
平行吗?观察你所在的教室,
你能找到相似的实例吗?
A1
B1
C1
D1
A
B
C
D
引入:
二.平行直线:
基本事实4
:平行于同一条直线的两条直线互相平行。
用符号语言表示如下:
已知a、b、c三条直线,若a‖c,且b‖c,则a‖b
a
b
c
基本事实4
表述的性质通常叫做空间平行线的传递性
例1.
已知ABCD是四个顶点不在同一个平面内的空间四边形,E、F、G、H分别是AB、BC、CD、DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。
A
B
C
D
E
F
G
H
∵
EH是△ABD的中位线
∴EH
∥BD且EH
=
1/2
BD
同理,FG
∥BD且FG
=1/2
BD
∴EH
∥FG且EH
=FG
∴四边形EFGH是一个平行四边形
证明:
连结BD
思考:在例2中,如果再加上AC=BD,那么四边形EFGH是什么图形?
2
1
3
1、等角定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
B
C
A
B?
C?
A?
空间中如果两个角的两边分别对应平行,且方向相同,那么这两个角相等.
2、
异面直线所成的角
a
b
o
aˊ
bˊ
设a、b为两异面直线,经过空间任一点O作直线
,我们把
所成的锐角(或直角)
叫做异面直线a与b所成的角(或夹角).
a
b
a
'
b'
o
a
'
b
'
o
'
a
O
b
a
'
3、两异面直线的夹角的取值范围:
若两条异面直线a、b的夹角为90?,则称这两条异面直线互相垂直,仍记作a⊥b
。
A
D
C
B
A1
B1
C1
D1
【思考1】在正方体
ABCD
-A1B1C1D1中,哪些棱所在直线与直线AA1垂直?
直线AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1分别与直线AA1垂直。
3、两异面直线的夹角的取值范围:
若两条异面直线a、b的夹角为90?,则称这两条异面直线互相垂直,仍记作a⊥b
。
【思考2】在平面内,垂直于同一条直线的两直线的位置关系如何?
在空间呢?
A
D
C
B
A1
B1
C1
D1
考点一、求异面直线的夹角
【例2】在正方体
ABCD
-A1B1C1D1中,
求直线A1B与C1C
的夹角。
解:∵BB1
‖CC1
,且∠A1BB1是锐角,
∴∠A1BB1是异面直线A1B与C1C
的夹角
∵∠A1BB1
=45°
∴异面直线A1B与C1C
的夹角为45°
方法小结:
求异面直线的夹角,关键是找到“相等的平面角”,将空间问题,转化为平面问题
二证
一作
三计算
作出或找出两异面直线所成的平面角,做平行线;
利用定义证明作出或找出的角是两异面直线所成的角;
把作出的角放在三角形中,解三角形
平移直线得出的角有可能是两条异面直线所成角的补角
(1)AD,
DC,
CC1,
B1C1,
DD1,
D1C1
(2)因为BB1
‖CC1
,
且∠A1BB1是
锐角,
所以∠A1BB1是异面直线A1B与
C1C
的夹角
因为∠A1BB1
=45°
所以异面直线A1B与C1C
的夹角为45°
例3、在正方体
ABCD
-A1B1C1D1中,
(1)哪些棱所在直线与直线A1B是异面直线?
(2)求直线A1B与C1C
的夹角;
(3)哪些棱所在直线与直线AA1垂直?
A
D
C
B
A1
B1
C1
D1
解:
(3)直线AB,
BC,
CD,
DA,
A1B1,
B1C1’
C1D1,
D1A1
分别与直线AA1垂直.
G
分析:
求异面直线的夹角,关键是找到
“相等的平面角”
由此可选取BD的中点G,连结GE,GF,
则异面直线EF和AB的夹角就是∠1或其补角
1
求异面直线的夹角
解:取BD的中点G,连结GE,GF,
∴∠1或其补角就是EF和AB所成角
G
1
求异面直线的夹角
A
B
C
F
E
G
D
A
C
B
A1
B1
C1
小结:
1.掌握等角定理
2.理解并会求异面直线所成的角
二证
一作
三计算
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
