六年级数学下册课件-5. 数学广角 鸽巢问题 -人教版(共19张PPT)
文档属性
| 名称 | 六年级数学下册课件-5. 数学广角 鸽巢问题 -人教版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 10:00:13 | ||
图片预览



文档简介
鸽巢问题
数学人教版六年级下册 第五单元
数学广角
一副扑克牌,取出大小王,还剩52张,随意抽出5张,至少有2张牌是同花色的。你相信吗?你能解释其中的道理吗?
例1:把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔。这是为什么?
知识点一:
把4支笔放进3个笔筒中,会有哪几种情况呢?
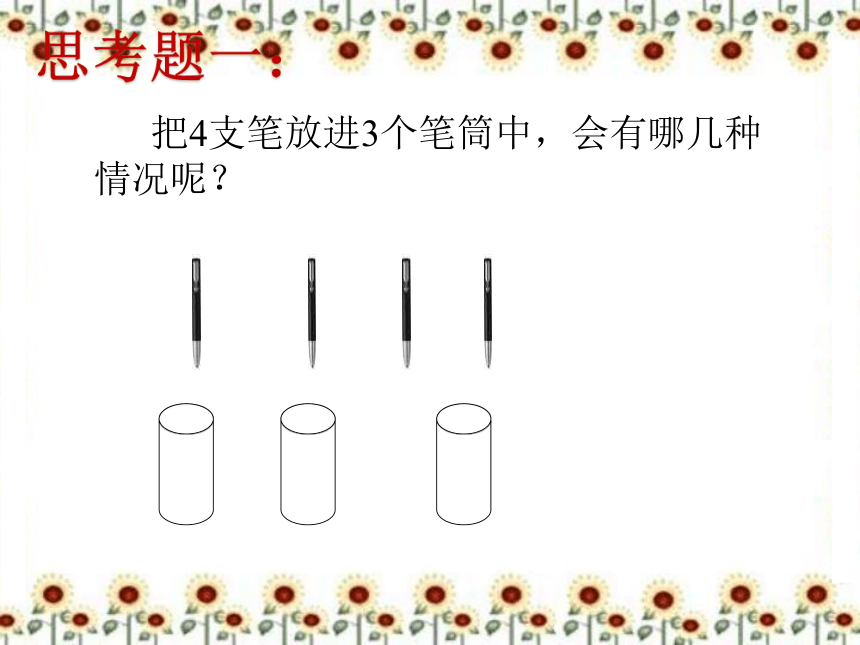
思考题一:
把4支笔放进3个笔筒中,会有哪几种情况呢?
把4支笔放进3个笔筒中,会有哪几种情况呢?
把4支笔放进3个笔筒中,会有哪几种情况呢?
至少放进2支笔
枚举法
4÷ 3 = 1……1
1+1=2
假设法
思考二:
4÷ 3 = 1……1
1+1=2
枚举法
假设法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6
5
7÷ 5 = 1……2
5
7
6÷ 5 = 1……1 1+1=2
知识点二:
7÷ 5 = 1……2
1+1=2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6÷ 5 = 1……1 1+1=2
7÷ 5 = 1……2 1+1=2
8÷ 5 = 1……3 1+1=2
9÷ 5 = 1……4 1+1=2
10÷ 5 = 2 2=2
11÷ 5 = 2……1 2+1=3
5
5
5
5
5
5
6
7
8
9
10
11
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6
5
6÷ 5 = 1……1 1+1=2
7
5
7÷ 5 = 1……2 1+1=2
8
5
8÷ 5 = 1……3 1+1=2
9
5
9÷ 5 = 1……4 1+1=2
11
5
11÷ 5 = 2……1 2+1=3
我的发现:
让鸽子飞进鸽笼里,如果平均分后有剩余,那么总有一个鸽笼里至少有“商+1”只。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
10
5
10÷ 5 = 2 2=2
我的发现:
如果正好分完,则至少数等于商。
像上面这样的问题就是“鸽巢问题”,
亦称“抽屉原理”。
一副扑克牌,取出大小王,还剩52张,随意抽出5张,至少有2张牌是同花色的。你相信吗?你能解释其中的道理吗?
四种花色
抽 牌
观察
分析
证明
初步认识鸽巢原理
一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?
想一想:
本次学习结束,
下次再见!
数学人教版六年级下册 第五单元
数学广角
一副扑克牌,取出大小王,还剩52张,随意抽出5张,至少有2张牌是同花色的。你相信吗?你能解释其中的道理吗?
例1:把4支笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2支笔。这是为什么?
知识点一:
把4支笔放进3个笔筒中,会有哪几种情况呢?
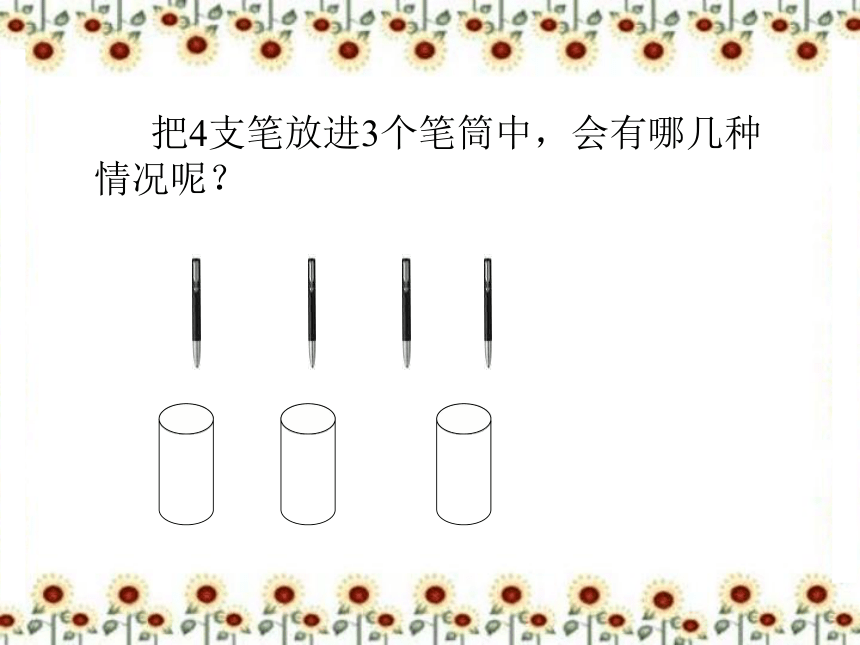
思考题一:
把4支笔放进3个笔筒中,会有哪几种情况呢?
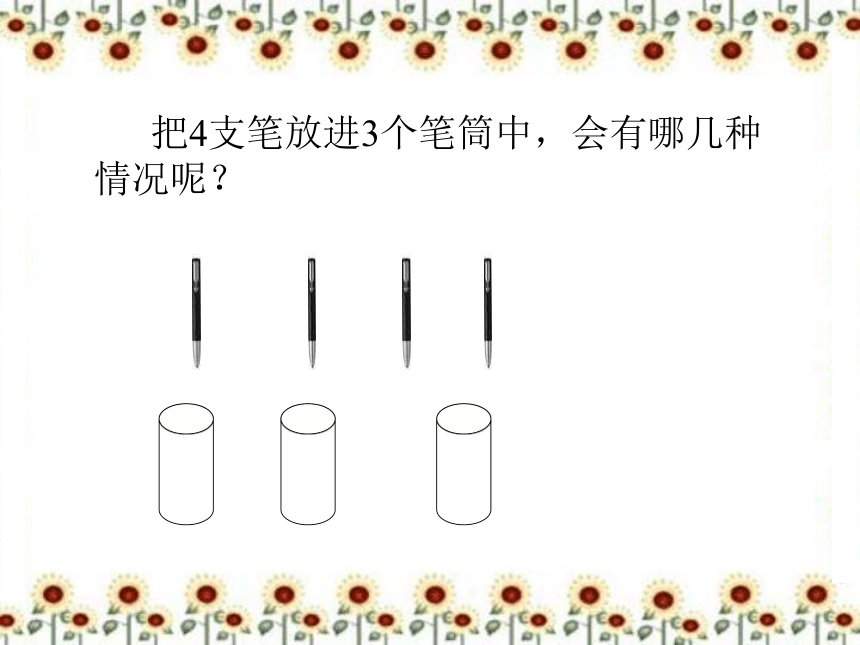
把4支笔放进3个笔筒中,会有哪几种情况呢?
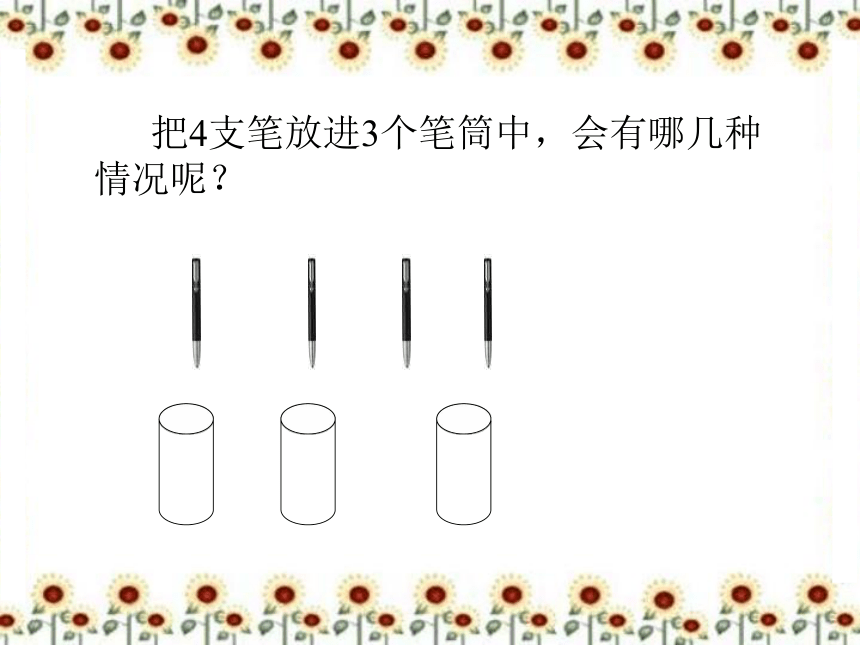
把4支笔放进3个笔筒中,会有哪几种情况呢?
至少放进2支笔
枚举法
4÷ 3 = 1……1
1+1=2
假设法
思考二:
4÷ 3 = 1……1
1+1=2
枚举法
假设法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6
5
7÷ 5 = 1……2
5
7
6÷ 5 = 1……1 1+1=2
知识点二:
7÷ 5 = 1……2
1+1=2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6÷ 5 = 1……1 1+1=2
7÷ 5 = 1……2 1+1=2
8÷ 5 = 1……3 1+1=2
9÷ 5 = 1……4 1+1=2
10÷ 5 = 2 2=2
11÷ 5 = 2……1 2+1=3
5
5
5
5
5
5
6
7
8
9
10
11
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
6
5
6÷ 5 = 1……1 1+1=2
7
5
7÷ 5 = 1……2 1+1=2
8
5
8÷ 5 = 1……3 1+1=2
9
5
9÷ 5 = 1……4 1+1=2
11
5
11÷ 5 = 2……1 2+1=3
我的发现:
让鸽子飞进鸽笼里,如果平均分后有剩余,那么总有一个鸽笼里至少有“商+1”只。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}鸽子数量
鸽笼数量
总有一个鸽笼至少飞进几只鸽子?
10
5
10÷ 5 = 2 2=2
我的发现:
如果正好分完,则至少数等于商。
像上面这样的问题就是“鸽巢问题”,
亦称“抽屉原理”。
一副扑克牌,取出大小王,还剩52张,随意抽出5张,至少有2张牌是同花色的。你相信吗?你能解释其中的道理吗?
四种花色
抽 牌
观察
分析
证明
初步认识鸽巢原理
一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?
想一想:
本次学习结束,
下次再见!
