安徽省青阳县第一中学2020-2021学年高二下学期3月月考文科数学试题 Word版含答案
文档属性
| 名称 | 安徽省青阳县第一中学2020-2021学年高二下学期3月月考文科数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 436.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 13:47:36 | ||
图片预览


文档简介
青阳一中2020-2021学年度3月份月考
高二数学试卷(文科)
考试时间:120分钟;
第I卷(选择题)
一、单选题:本题共12小题,每小题5分,共60分。在每小题的四个选项中,只有一个选项是符合题目要求的.
1.复数false(false为虚数单位)等于()
A.false B.false C.false D.false
2.在一组样本数据false,false,…,false(false,false,false,…,false互不相等)的散点图中,若所有样本点false都在直线,false上,则这组样本数据的样本相关系数为( )
A.false B.0 C.false D.1
3.商家生产一种产品,需要先进行市场调研,计划对北京、上海、广州三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是( )
A. B.
C. D.
4.给出一个命题p:若false,且false,则a,b,c,d中至少有一个小于零,在用反证法证明p时,应该假设( )
A.a,b,c,d中至少有一个正数 B.a,b,c,d全为正数
C.a,b,c,d全都大于或等于0 D.a,b,c,d中至多有一个负数
5.已知false的三个内角false,false,false的对边边长分别为false,false,false,若false,false,则false( )
A.false B.false C.false D.false
6.随机调查false名性别不同的大学生是否喜欢打羽毛球,得到如下false列联表:
男
女
总计
喜欢打羽毛球
false
false
false
不喜欢打羽毛球
false
false
false
总计
false
false
false
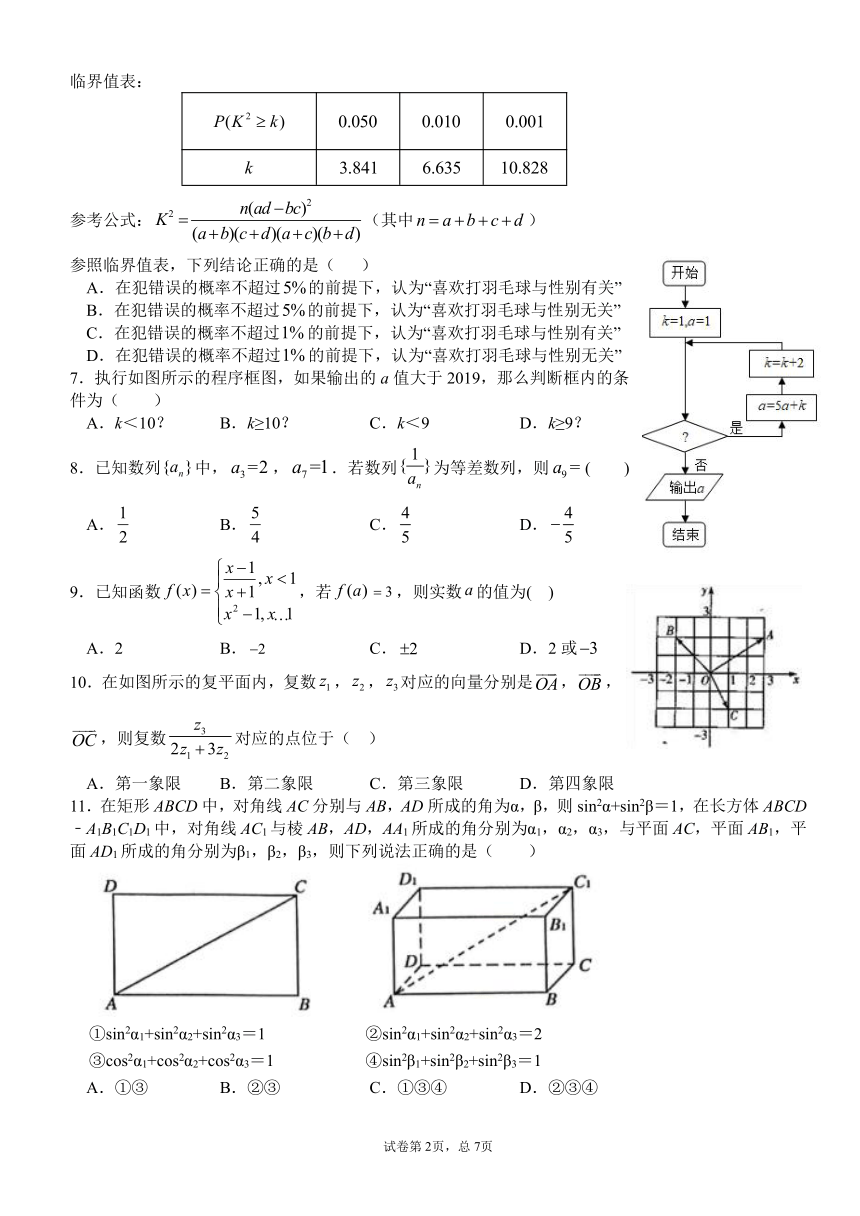
临界值表:
false
false
false
false
false
false
false
false
5036185488950参考公式:false(其中false)
参照临界值表,下列结论正确的是( )
A.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别有关”
B.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别无关”
C.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别有关”
D.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别无关”
7.执行如图所示的程序框图,如果输出的a值大于2019,那么判断框内的条件为( )
A.k<10? B.k≥10? C.k<9 D.k≥9?
8.已知数列false中,false,false.若数列false为等差数列,则false( )
A.false B.false C.false D.false
48933103384559.已知函数false,若falsefalse,则实数false的值为( )
A.2 B.false C.false D.2或false
10.在如图所示的复平面内,复数false,false,false对应的向量分别是false,false,false,则复数false对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.在矩形ABCD中,对角线AC分别与AB,AD所成的角为α,β,则sin2α+sin2β=1,在长方体ABCD﹣A1B1C1D1中,对角线AC1与棱AB,AD,AA1所成的角分别为α1,α2,α3,与平面AC,平面AB1,平面AD1所成的角分别为β1,β2,β3,则下列说法正确的是( )
①sin2α1+sin2α2+sin2α3=1 ②sin2α1+sin2α2+sin2α3=2
③cos2α1+cos2α2+cos2α3=1 ④sin2β1+sin2β2+sin2β3=1
A.①③ B.②③ C.①③④ D.②③④
12.已知函数false,若对任意false,false恒成立,则false的取值范围是( )
A.false B.false C.false D.false
第II卷(非选择题)
二、填空题:本题共4小题,每小题5分,共20分.
13.设x,y满足约束条件false,false的最大值为______.
14.若复数z=1+2i,其中i是虚数单位,则false=________.
15.甲、乙、丙、丁四人参加比赛,有3人分别获得一等奖、二等奖和三等奖,另外1人没获奖.甲说:乙获得奖;乙说:丙获得了一等奖;丙说:丁没有获得二等奖;如果甲、乙、丙中有一人获得了一等奖,而且只有获得一等奖的那个人说的是真话,则获得一等奖的是__________.
16.已知都是质数,且则的值为________.
三、解答题本题共6小题,共70分,解答应写出文字说明、证明过程和演算步骤.
17.(本小题满分10分)
已知复数false.当实数false取什么值时,复数false是:
(1)纯虚数;
(2)复平面内第二、四象限角平分线上的点对应的复数.
18.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量false(吨)与相应的生产能耗false(吨标准煤)的几组对应数据.
false
3
4
5
6
7
false
3
3
4
5
5
(1)请根据上表提供的数据,用最小二乘法求出false关于false的线性回归方程false;
(2)已知该厂技改前,100吨甲产品的生产能耗为70吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
参考公式false,false
19. (本小题满分12分)
(1)证明:求证false.
(2)设false,false,false都是正数,求证:false;
20.(本小题满分12分)
在如图所示的正方体false中,false,false分别是false,false的中点.证明:
460756014605(1)false面false;
(2)false.
21.(本小题满分12分)
2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占false,而男生有10人表示对冰球运动没有兴趣额.
(1)完成false列联表,并回答能否有false的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣
没兴趣
合计
男
55
女
合计
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
false
0.150
0.100
0.050
0.025
0.010
false
2.072
2.706
3.841
5.024
6.635
false
22.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)当false时,若函数false在false上的最小值是false,求false的值。
高二3月月考文科数学参考答案
1-5 B A D C B 6-10 C A C C C 11-12 D A
13.false 14.6 15.甲 16.78.
17.(1)false(2)false
由于false,复数false可表示为false
(1)当false,且false即false时,false为纯虚数.
(2)当false即false时,false为复平面内第二、四象限角平分线上的点对应的复数.
18.(1)false;(2)9(吨标准煤).
解:(1)由对应数据,计算得
false,false
false
false
false,
所求的回归方程为false
(2)false,false,
预测生产100吨甲产品的生产能耗比技改前降低false(吨标准煤).
19.(1)证明:要证false,
只需证明false,
即证明false,
也就是证明false,
上式显然成立,故原不等式成立.
(2)由题意,因为false
falsefalse,
所以false,当且仅当false时,等号成立.
20.(1)有(2)false
【详解】
(1)根据已知数据得到如下列联表
有兴趣
没有兴趣
合计
男
45
10
55
女
30
15
45
合计
75
25
100
由列联表中的数据可得
因为,
所以有90%的把握认为“对冰球是否有兴趣与性别有关”.
(2)记5人中对冰球有兴趣的3人为A、B、C,对冰球没有兴趣的2人为m、n,
则从这5人中随机抽取3人,所有可能的情况为:(A,m,n),(B,m,n),(C,m,n),(A,B,m),
(A,B,n),(B,C,m),(B,C,n),(A,C,m),(A,C,n),(A,B,C),共10种情况,
其中3人都对冰球有兴趣的情况有(A,B,C),共1种,2人对冰球有兴趣的情况有(A,B,m),(A,B,n),(B,C,m),(B,C,n),(A,C,m),(A,C,n),共6种,
所以至少2人对冰球有兴趣的情况有7种,
因此,所求概率为false.
20.【详解】证明:如图所示:
(1)取false中点false,连接false,false,
false、false、false分别正方体是棱false,false的中点,
所以false,且false.
所以四边形false为平行四边形,
所以false,
false面false,false面false
所以false面false.
(2)连接false,
在正方体false中,
所以false面false,false面false,
所以false
又false,false,
所以false面false,
又false面false,
所以false.
22.【详解】
(1)定义域为false,求得false,
当false时,false,故false在false单调递增 ,
当false时,令false,得 false,所以当false时,false,false单调递减
当false时,false,false单调递增.
(2)当false时,由(1)知false在false上单调递增,所以 false(舍去),
当false时,由(1)知false在false单调递减,在false单调递增
所以false,解得false (舍去),
当false时,由(1)知false在false单调递减,
所以false,解得false ,
综上所述,false.
高二数学试卷(文科)
考试时间:120分钟;
第I卷(选择题)
一、单选题:本题共12小题,每小题5分,共60分。在每小题的四个选项中,只有一个选项是符合题目要求的.
1.复数false(false为虚数单位)等于()
A.false B.false C.false D.false
2.在一组样本数据false,false,…,false(false,false,false,…,false互不相等)的散点图中,若所有样本点false都在直线,false上,则这组样本数据的样本相关系数为( )
A.false B.0 C.false D.1
3.商家生产一种产品,需要先进行市场调研,计划对北京、上海、广州三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是( )
A. B.
C. D.
4.给出一个命题p:若false,且false,则a,b,c,d中至少有一个小于零,在用反证法证明p时,应该假设( )
A.a,b,c,d中至少有一个正数 B.a,b,c,d全为正数
C.a,b,c,d全都大于或等于0 D.a,b,c,d中至多有一个负数
5.已知false的三个内角false,false,false的对边边长分别为false,false,false,若false,false,则false( )
A.false B.false C.false D.false
6.随机调查false名性别不同的大学生是否喜欢打羽毛球,得到如下false列联表:
男
女
总计
喜欢打羽毛球
false
false
false
不喜欢打羽毛球
false
false
false
总计
false
false
false
临界值表:
false
false
false
false
false
false
false
false
5036185488950参考公式:false(其中false)
参照临界值表,下列结论正确的是( )
A.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别有关”
B.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别无关”
C.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别有关”
D.在犯错误的概率不超过false的前提下,认为“喜欢打羽毛球与性别无关”
7.执行如图所示的程序框图,如果输出的a值大于2019,那么判断框内的条件为( )
A.k<10? B.k≥10? C.k<9 D.k≥9?
8.已知数列false中,false,false.若数列false为等差数列,则false( )
A.false B.false C.false D.false
48933103384559.已知函数false,若falsefalse,则实数false的值为( )
A.2 B.false C.false D.2或false
10.在如图所示的复平面内,复数false,false,false对应的向量分别是false,false,false,则复数false对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.在矩形ABCD中,对角线AC分别与AB,AD所成的角为α,β,则sin2α+sin2β=1,在长方体ABCD﹣A1B1C1D1中,对角线AC1与棱AB,AD,AA1所成的角分别为α1,α2,α3,与平面AC,平面AB1,平面AD1所成的角分别为β1,β2,β3,则下列说法正确的是( )
①sin2α1+sin2α2+sin2α3=1 ②sin2α1+sin2α2+sin2α3=2
③cos2α1+cos2α2+cos2α3=1 ④sin2β1+sin2β2+sin2β3=1
A.①③ B.②③ C.①③④ D.②③④
12.已知函数false,若对任意false,false恒成立,则false的取值范围是( )
A.false B.false C.false D.false
第II卷(非选择题)
二、填空题:本题共4小题,每小题5分,共20分.
13.设x,y满足约束条件false,false的最大值为______.
14.若复数z=1+2i,其中i是虚数单位,则false=________.
15.甲、乙、丙、丁四人参加比赛,有3人分别获得一等奖、二等奖和三等奖,另外1人没获奖.甲说:乙获得奖;乙说:丙获得了一等奖;丙说:丁没有获得二等奖;如果甲、乙、丙中有一人获得了一等奖,而且只有获得一等奖的那个人说的是真话,则获得一等奖的是__________.
16.已知都是质数,且则的值为________.
三、解答题本题共6小题,共70分,解答应写出文字说明、证明过程和演算步骤.
17.(本小题满分10分)
已知复数false.当实数false取什么值时,复数false是:
(1)纯虚数;
(2)复平面内第二、四象限角平分线上的点对应的复数.
18.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量false(吨)与相应的生产能耗false(吨标准煤)的几组对应数据.
false
3
4
5
6
7
false
3
3
4
5
5
(1)请根据上表提供的数据,用最小二乘法求出false关于false的线性回归方程false;
(2)已知该厂技改前,100吨甲产品的生产能耗为70吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
参考公式false,false
19. (本小题满分12分)
(1)证明:求证false.
(2)设false,false,false都是正数,求证:false;
20.(本小题满分12分)
在如图所示的正方体false中,false,false分别是false,false的中点.证明:
460756014605(1)false面false;
(2)false.
21.(本小题满分12分)
2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占false,而男生有10人表示对冰球运动没有兴趣额.
(1)完成false列联表,并回答能否有false的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣
没兴趣
合计
男
55
女
合计
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
false
0.150
0.100
0.050
0.025
0.010
false
2.072
2.706
3.841
5.024
6.635
false
22.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)当false时,若函数false在false上的最小值是false,求false的值。
高二3月月考文科数学参考答案
1-5 B A D C B 6-10 C A C C C 11-12 D A
13.false 14.6 15.甲 16.78.
17.(1)false(2)false
由于false,复数false可表示为false
(1)当false,且false即false时,false为纯虚数.
(2)当false即false时,false为复平面内第二、四象限角平分线上的点对应的复数.
18.(1)false;(2)9(吨标准煤).
解:(1)由对应数据,计算得
false,false
false
false
false,
所求的回归方程为false
(2)false,false,
预测生产100吨甲产品的生产能耗比技改前降低false(吨标准煤).
19.(1)证明:要证false,
只需证明false,
即证明false,
也就是证明false,
上式显然成立,故原不等式成立.
(2)由题意,因为false
falsefalse,
所以false,当且仅当false时,等号成立.
20.(1)有(2)false
【详解】
(1)根据已知数据得到如下列联表
有兴趣
没有兴趣
合计
男
45
10
55
女
30
15
45
合计
75
25
100
由列联表中的数据可得
因为,
所以有90%的把握认为“对冰球是否有兴趣与性别有关”.
(2)记5人中对冰球有兴趣的3人为A、B、C,对冰球没有兴趣的2人为m、n,
则从这5人中随机抽取3人,所有可能的情况为:(A,m,n),(B,m,n),(C,m,n),(A,B,m),
(A,B,n),(B,C,m),(B,C,n),(A,C,m),(A,C,n),(A,B,C),共10种情况,
其中3人都对冰球有兴趣的情况有(A,B,C),共1种,2人对冰球有兴趣的情况有(A,B,m),(A,B,n),(B,C,m),(B,C,n),(A,C,m),(A,C,n),共6种,
所以至少2人对冰球有兴趣的情况有7种,
因此,所求概率为false.
20.【详解】证明:如图所示:
(1)取false中点false,连接false,false,
false、false、false分别正方体是棱false,false的中点,
所以false,且false.
所以四边形false为平行四边形,
所以false,
false面false,false面false
所以false面false.
(2)连接false,
在正方体false中,
所以false面false,false面false,
所以false
又false,false,
所以false面false,
又false面false,
所以false.
22.【详解】
(1)定义域为false,求得false,
当false时,false,故false在false单调递增 ,
当false时,令false,得 false,所以当false时,false,false单调递减
当false时,false,false单调递增.
(2)当false时,由(1)知false在false上单调递增,所以 false(舍去),
当false时,由(1)知false在false单调递减,在false单调递增
所以false,解得false (舍去),
当false时,由(1)知false在false单调递减,
所以false,解得false ,
综上所述,false.
同课章节目录
