2021年人教版八年级下册第18章《平行四边形》专题提升:以平行四边形为背景的计算与证明(word版含解析)
文档属性
| 名称 | 2021年人教版八年级下册第18章《平行四边形》专题提升:以平行四边形为背景的计算与证明(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 338.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 15:01:33 | ||
图片预览

文档简介
2021年人教版八年级下册第18章《平行四边形》专题提升
以平行四边形为背景的计算与证明
角度的计算与证明(一证一求)
1.如图,点E是?ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)证明:AD=CF.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
2.如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
3.如图,点E在BC上,△ABC≌△EAD.
(1)求证:四边形ABCD是平行四边形;
(2)若AE平分∠DAB.∠EDC=30°,求∠AED的度数.
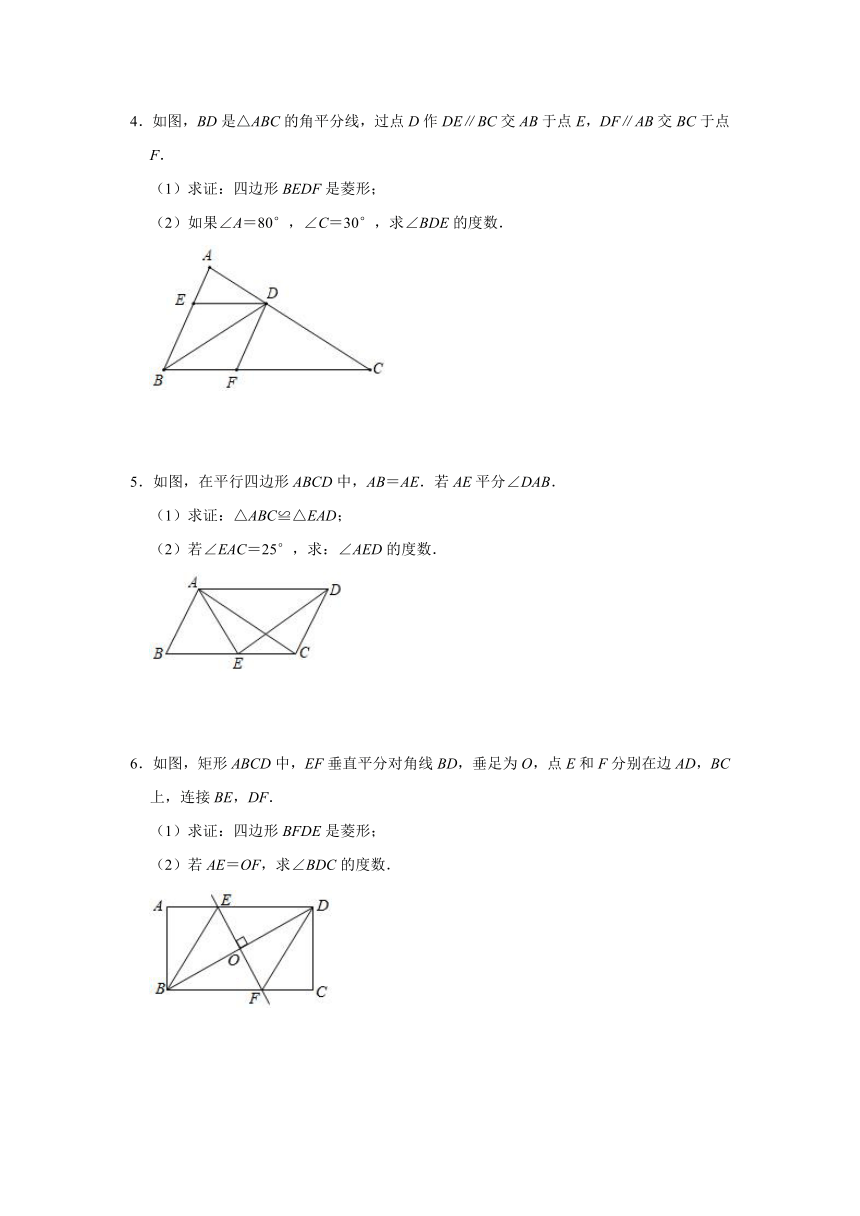
4.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.
5.如图,在平行四边形ABCD中,AB=AE.若AE平分∠DAB.
(1)求证:△ABC≌△EAD;
(2)若∠EAC=25°,求:∠AED的度数.
6.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF.
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
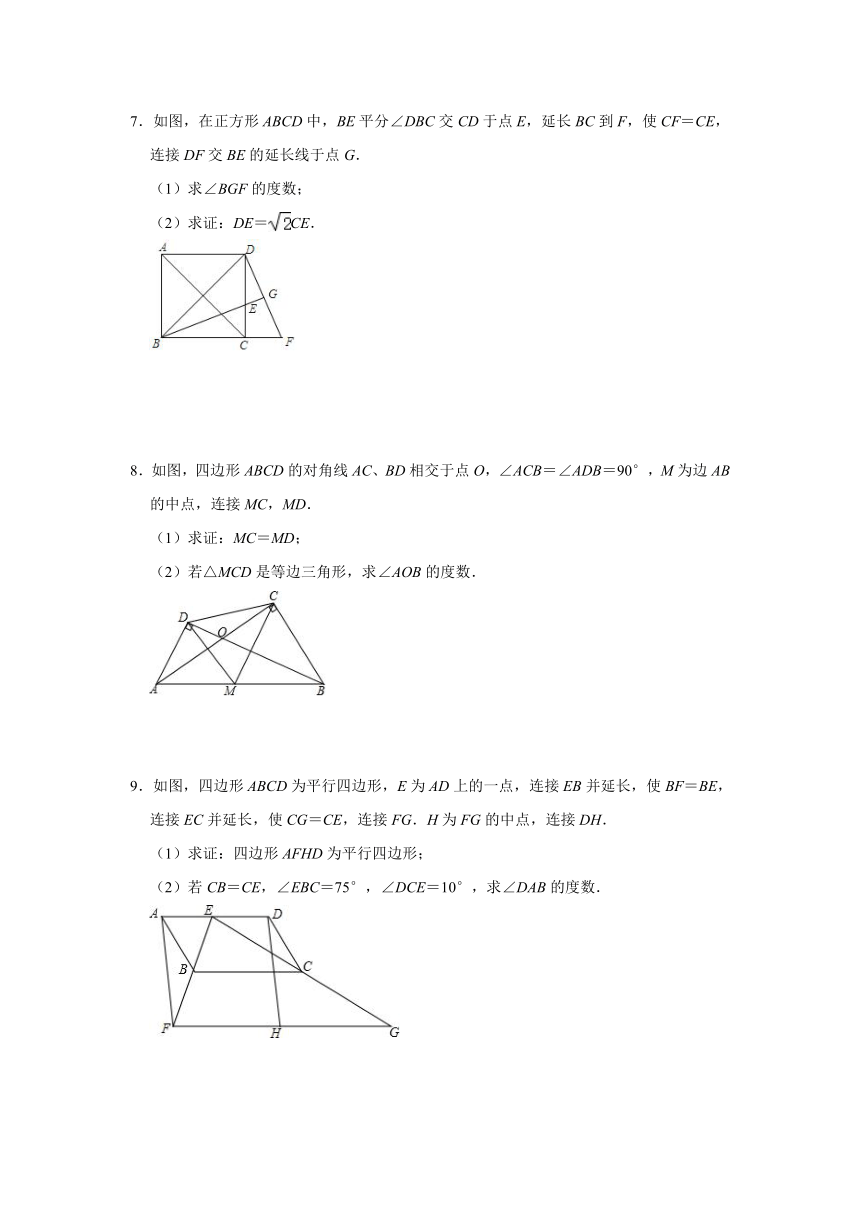
7.如图,在正方形ABCD中,BE平分∠DBC交CD于点E,延长BC到F,使CF=CE,连接DF交BE的延长线于点G.
(1)求∠BGF的度数;
(2)求证:DE=CE.
8.如图,四边形ABCD的对角线AC、BD相交于点O,∠ACB=∠ADB=90°,M为边AB的中点,连接MC,MD.
(1)求证:MC=MD;
(2)若△MCD是等边三角形,求∠AOB的度数.
9.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数.
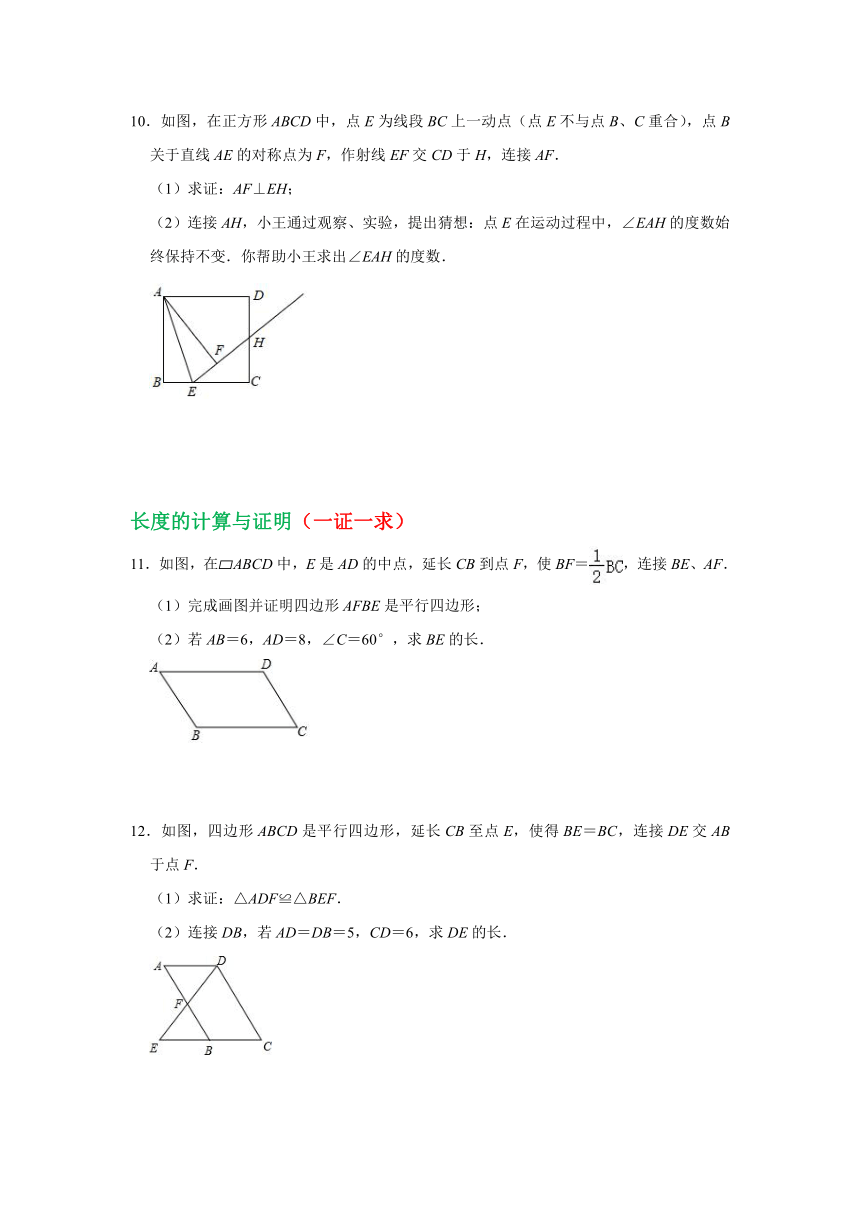
10.如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.
(1)求证:AF⊥EH;
(2)连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.
长度的计算与证明(一证一求)
11.如图,在?ABCD中,E是AD的中点,延长CB到点F,使BF=,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.
12.如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连接DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连接DB,若AD=DB=5,CD=6,求DE的长.
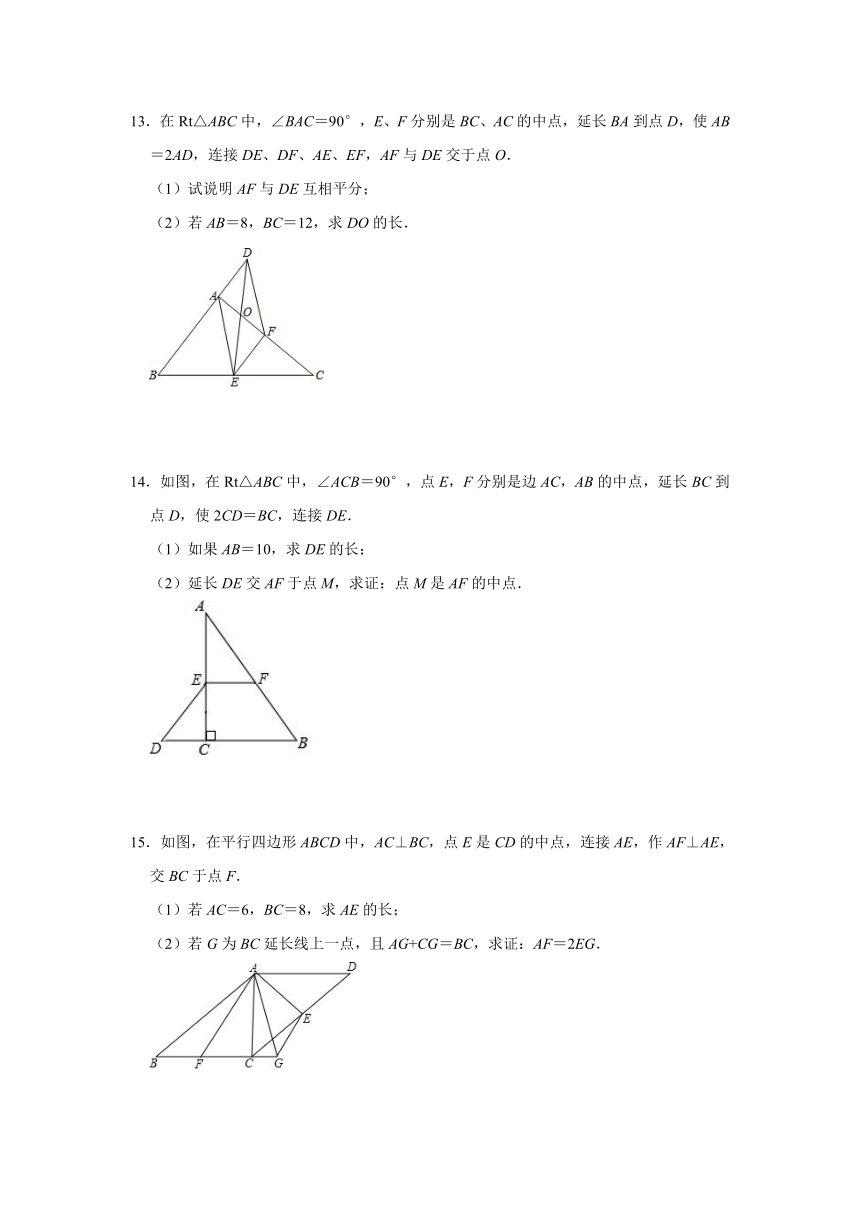
13.在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
(1)试说明AF与DE互相平分;
(2)若AB=8,BC=12,求DO的长.
14.如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.
(1)如果AB=10,求DE的长;
(2)延长DE交AF于点M,求证:点M是AF的中点.
15.如图,在平行四边形ABCD中,AC⊥BC,点E是CD的中点,连接AE,作AF⊥AE,交BC于点F.
(1)若AC=6,BC=8,求AE的长;
(2)若G为BC延长线上一点,且AG+CG=BC,求证:AF=2EG.
16.如图,在?ABCD中,∠ACB=45°,AE⊥BC于点E,过点C作CF⊥AB于点F,交AE于点M.点N在边BC上,且AM=CN,连接DN.
(1)若AB=,AC=4,求BC的长;
(2)求证:AD+AM=DN.
17.如图,在?ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.
(1)求证:AF⊥DE,BF=CE.
(2)若AD=10,AB=6,AF=8,求DE的长度.
18.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
19.已知:如图,在?ABCD中,∠BCD的平分线CE交AD于E,∠ABC的平分线BG交CE于F,交AD于G.
(1)试找出图中的等腰三角形,并选择一个加以说明.
(2)试说明:AE=DG.
(3)若BG将AD分成3:2的两部分,且AD=10,求?ABCD的周长.
参考答案
角度的计算与证明(一证一求)
1.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,,
∴△ADE≌△FCE(AAS),
∴CF=AD;
(2)∵∠BAF=90°,
添加一个条件:当∠B=60°时,∠F=90°﹣60°=30°(答案不唯一).
2.【解答】(1)证明∵E为AD的中点,
∴DE=AE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠EDC=∠EAF,
在△DEC和△AEF中,,
∴△DEC≌△AEF(AAS),
∴DC=FA,
∵AD=2AB,
∴AB=DE=EA=FA,
∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,
∴∠AEB=∠ABE,
∴∠EBC=∠ABE=35°.
3.【解答】(1)证明:∵△ABC≌△EAD,
∴BC=AD,∠B=∠EAD,AB=EA,
∴∠B=∠AEB,
∴∠EAD=∠AEB,
∴BC∥AD,
∴四边形ABCD是平行四边形;
(2)解:由(1)得:∠B=∠AEB=∠EAD,四边形ABCD是平行四边形,
∴∠ADC=∠B,
∵AE平分∠DAB,
∴∠BAE=∠EAD,
∴∠B=∠AEB=∠BAE,
∴△ABE是等边三角形,
∴∠ADC=∠B=∠BAE=∠EAD=60°,
∴∠ADE=∠ADC﹣∠EDC=60°﹣30°=30°,
∴∠AED=190°﹣60°﹣30°=90°.
4.【解答】(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°﹣80°﹣30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,
∴∠BDE=∠EDF=35°.
5.【解答】解:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
在△ABC和△AED中,
,
∴△ABC≌△EAD(SAS),
(2)∵△ABC≌△EAD,
∴∠AED=∠BAC,
∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°,
∴∠AED=85°.
6.【解答】(1)证明:∵EF垂直平分对角线BD,
∴∠DOE=∠BOF=90°,OB=OD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(AAS),
∴DE=BF,
∵EF垂直平分对角线BD,
∴DE=BE,BF=DF,
∴DE=BE=BF=DF,
∴四边形BFDE是菱形;
(2)解:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,
∵∠BOF=90°,
∴∠A=∠BOF=90°,
在Rt△BAE和Rt△BOF中,
,
∴Rt△BAE≌Rt△BOF(HL),
∴AB=OB,
∵AB=CD,OB=OD,
∴CD=BD,
∵∠C=90°,
∴∠CBD=30°,
∴∠BDC=180°﹣∠C﹣∠CBD=60°.
7.【解答】解:(1)∵在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴∠BEC=∠DFC,
∵∠BEC+∠CBE=90°,
∴∠CBE+∠DFC=90°,
∴∠BGF=90°;
(2)连接EF,
∵BE平分∠DBC,
∴∠DBG=∠CBG,
∵BG=BG,∠BGD=∠BGF=90°,
∴△BDG≌△BFG(ASA),
∴DG=FG,
∴BG垂直平分DF,
∴DE=FE,
∵CE2+CF2=EF2,CE=CF,
∴,
∴DE=CE.
8.【解答】(1)证明:∵∠ACB=∠ADB=90°,M为边AB的中点,
∴MC=AB,MD=AB,
∴MC=MD;
(2)解:∵MC=MD=AB=AM=BM,
∴∠BAC=∠ACM,∠ABD=∠BDM,
∴∠BMC=2∠BAC,∠AMD=2∠ABD,
∵△MCD是等边三角形,
∴∠DMC=60°,
∴∠BMC+∠AMD=120°,
∴2∠BAC+2∠ABD=120°,
∴∠BAO+∠ABO=60°,
∴∠AOB=180°﹣60°=120°.
9.【解答】(1)证明:∵BF=BE,CG=CE,
∴BC为△FEG的中位线,
∴BC∥FG,BC=FG,
又∵H是FG的中点,
∴FH=FG,
∴BC=FH.
又∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,
∵CE=CB,
∴∠BEC=∠EBC=75°,
∴∠BCE=180°﹣75°﹣75°=30°,
∴∠DCB=∠DCE+∠BCE=10°+30°=40°,
∴∠DAB=40°.
10.【解答】解:(1)证明:∵点B关于直线AE的对称点为F,
∴AB=AF,BE=EF,
又∵AE=AE,
∴△ABE≌△AFE(SSS),
∴∠AFE=∠B=90°,
∴AF⊥EH;
(2)连接AH,如图:
由(1)得AB=AF,AF⊥EH,
∴AF=AD,∠D=∠AFH=90°,AH=AH,
∴△AFH≌△ADH(HL),
∴∠FAH=∠DAH,
又∵∠BAE=∠FAE,在正方形ABCD中,∠BAD=90°,
∴∠EAH=45°.
长度的计算与证明(一证一求)
11.【解答】证明:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又E是AD的中点,,
∴AE∥BF,AE=BF,
∴四边形AFBE是平行四边形;
(2)过点A作AG⊥BF于G,
由?ABCD可知∠ABF=∠C=60°,
又AB=6,AD=8,
∴BG=3,FG=1,AG=,
∴BE=AF=.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠A=∠FBE,∠ADF=∠E
又∵BC=BE,
∴AD=BE,
在△ADF和△BEF中,,
∴△ADF≌△BEF(ASA);
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD=6,AD=BC,
由(1)得:△ADF≌△BEF,
∴AD=BE,EF=DF,AF=BF=AB=3,
∵AD=DB=5,
∴DB=BE=5,
∴BF⊥DE,
在Rt△BEF中,EF===4,
∴DE=2EF=2×4=8.
13.【解答】解:(1)∵E、F分别是BC、AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB且EF=AB.
又AB=2AD,即AD=AB,
∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,
∴AF与DE互相平分;
(2)∵在Rt△ABC中,∠BAC=90°,AB=8,BC=12,
∴由勾股定理得 AC===4
又由(1)知,OA=OF,且AF=CF,
∴OA=AC=.
∴在△AOD中,∠DAO=90°,AD=AB=4,OA=,
∴由勾股定理得 DO===.
14.【解答】解:(1)连接CF,
在Rt△ABC中,F是AB的中点,
∴CF=AB=5,
∵点E,F分别是边AC,AB的中点,
∴EF∥BC,EF=BC,
∵2CD=BC,
∴EF=CD,EF∥CD,
∴四边形EDCF是平行四边形,
∴DE=CF=5;
(2)如图2,∵四边形EDCF是平行四边形,
∴CF∥DM,
∵点E是边AC的中点,
∴点M是AF的中点.
15.【解答】(1)解:∵AC⊥BC,
∴∠ACB=90°,
∵AC=6,BC=8,
∴AB==10,
∵四边形ABCD是平行四边形,
∴CD=AB=10,AD∥BC
∴CA⊥AD,
∴∠CAD=90°,
∵CE=ED,
∴AE=CD=5.
(2)证明:延长AE交BC的延长线于M,在CB上取一点N,使得CN=CG,连接AN.
∵AD∥CM,
∴∠DAE=∠M,
在△DAE和△MCE中,,
∴△DAE≌△MCE(AAS),
∴AE=EM,
∵AE=ED=EC,
∴AM=CD=AB,
∵AC⊥BM,
∴BC=CM,
∵AC⊥NG,CN=CG,
∴AG=AN,
∵AG+CG=BC,
∴BN=AG=AN,
∵CB=CM,CN=CG,
∴BN=GM,
∴GA=GM,
∵AE=EM,
∴EG⊥AM,
∵FA⊥AM,
∴EG∥AF,
∵AE=EM,
∴FG=GM,
∴EG=AF,
即AF=2EG.
16.【解答】(1)解:∵∠ACB=45°,AE⊥BC,
∴∠AEC=∠AEB=90°,△ACE是等腰直角三角形,
∴∠EAC=45°,AE=CE===2,
由勾股定理得:BE===,
∴BC=BE+CE=3;
(2)证明:延长AD至G,使DG=AM,连接CG,如图所示:
∵AM=CN,
∴DG=CN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∠B=∠ADC,
∴DG∥CN,
∴四边形CGDN是平行四边形,
∴CG=DN,
∵CF⊥AB,
∴∠CFB=90°=∠AEB=∠CEA,
∴∠BAE=∠MCE,
在△ABE和△CME中,,
∴△ABE≌△CME(AAS),
∴AB=CM,∠B=∠CME,
∴CM=CD,∠CME=∠ADC,
∴∠AMC=∠GDC,
在△ACM和△GCD中,,
∴△ACM≌△GCD(SAS),
∴∠G=∠MAC=45°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴△ACG是等腰直角三角形,
∴AG=CG,
∵AG=AD+DG=AD+AM,CG=DN,
∴AD+AM=DN.
17.【解答】(1)证明:在平行四边形ABCD中,AB∥DC,
∴∠BAD+∠ADC=180°.
∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAE=∠BAE=∠BAD,∠ADF=∠CDF=∠ADC.
∴∠DAE+∠ADF=∠BAD+∠ADC=90°.
∴∠AGD=90°.
∴AE⊥DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAF=∠AFB,
又∵∠DAF=∠BAF,
∴∠BAF=∠AFB,
∴AB=BF,
同理可得CD=CE,
∴BF=CE;
(2)解:过点C作CK∥AF交AD于K,交DE于点I,
∵AK∥FC,AF∥CK,
∴四边形AFCK是平行四边形,∠AGD=∠KID=90°,
∴AF=CK=8,
∵∠KDI+∠DKI=90°,∠DIC+∠DCI=90°,∠IDK=∠IDC,
∴∠DKI=∠DCI,
∴DK=DC=6,
∴KI=CI=4,
∵AD∥BC,
∴∠ADE=∠DEC=∠CDE,
∴CE=CD,
∵CI⊥DE,
∴EI=DI,
∵DI===2,
∴DE=2DI=4.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
19.【解答】解:(1)△ABG,△DCE是等腰三角形.
在平行四边形ABCD中,则AD∥BC,
∴∠AGB=∠GBC,
又BG平分∠ABC,
∴∠ABG=∠CBG,
∴∠ABG=∠AGB,即AB=AG,
∴△ABG是等腰三角形;
(2)由(1)可得AB=AG=CD=DE,
∴AE=DG;
(3)假设AG:GD=3:2,
∵AD=10,∴AB=AG=AD=6,
∴平行四边形的周长为2(10+6)=32;
当AG:GD=2:3时,则AB=AG=AD=4,
∴平行四边形的周长为2(10+4)=28.
所以平行四边形ABCD的周长为32或28.
以平行四边形为背景的计算与证明
角度的计算与证明(一证一求)
1.如图,点E是?ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)证明:AD=CF.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
2.如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
3.如图,点E在BC上,△ABC≌△EAD.
(1)求证:四边形ABCD是平行四边形;
(2)若AE平分∠DAB.∠EDC=30°,求∠AED的度数.
4.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.
5.如图,在平行四边形ABCD中,AB=AE.若AE平分∠DAB.
(1)求证:△ABC≌△EAD;
(2)若∠EAC=25°,求:∠AED的度数.
6.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF.
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
7.如图,在正方形ABCD中,BE平分∠DBC交CD于点E,延长BC到F,使CF=CE,连接DF交BE的延长线于点G.
(1)求∠BGF的度数;
(2)求证:DE=CE.
8.如图,四边形ABCD的对角线AC、BD相交于点O,∠ACB=∠ADB=90°,M为边AB的中点,连接MC,MD.
(1)求证:MC=MD;
(2)若△MCD是等边三角形,求∠AOB的度数.
9.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数.
10.如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.
(1)求证:AF⊥EH;
(2)连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.
长度的计算与证明(一证一求)
11.如图,在?ABCD中,E是AD的中点,延长CB到点F,使BF=,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.
12.如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连接DE交AB于点F.
(1)求证:△ADF≌△BEF.
(2)连接DB,若AD=DB=5,CD=6,求DE的长.
13.在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
(1)试说明AF与DE互相平分;
(2)若AB=8,BC=12,求DO的长.
14.如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.
(1)如果AB=10,求DE的长;
(2)延长DE交AF于点M,求证:点M是AF的中点.
15.如图,在平行四边形ABCD中,AC⊥BC,点E是CD的中点,连接AE,作AF⊥AE,交BC于点F.
(1)若AC=6,BC=8,求AE的长;
(2)若G为BC延长线上一点,且AG+CG=BC,求证:AF=2EG.
16.如图,在?ABCD中,∠ACB=45°,AE⊥BC于点E,过点C作CF⊥AB于点F,交AE于点M.点N在边BC上,且AM=CN,连接DN.
(1)若AB=,AC=4,求BC的长;
(2)求证:AD+AM=DN.
17.如图,在?ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.
(1)求证:AF⊥DE,BF=CE.
(2)若AD=10,AB=6,AF=8,求DE的长度.
18.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
19.已知:如图,在?ABCD中,∠BCD的平分线CE交AD于E,∠ABC的平分线BG交CE于F,交AD于G.
(1)试找出图中的等腰三角形,并选择一个加以说明.
(2)试说明:AE=DG.
(3)若BG将AD分成3:2的两部分,且AD=10,求?ABCD的周长.
参考答案
角度的计算与证明(一证一求)
1.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,,
∴△ADE≌△FCE(AAS),
∴CF=AD;
(2)∵∠BAF=90°,
添加一个条件:当∠B=60°时,∠F=90°﹣60°=30°(答案不唯一).
2.【解答】(1)证明∵E为AD的中点,
∴DE=AE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠EDC=∠EAF,
在△DEC和△AEF中,,
∴△DEC≌△AEF(AAS),
∴DC=FA,
∵AD=2AB,
∴AB=DE=EA=FA,
∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,
∴∠AEB=∠ABE,
∴∠EBC=∠ABE=35°.
3.【解答】(1)证明:∵△ABC≌△EAD,
∴BC=AD,∠B=∠EAD,AB=EA,
∴∠B=∠AEB,
∴∠EAD=∠AEB,
∴BC∥AD,
∴四边形ABCD是平行四边形;
(2)解:由(1)得:∠B=∠AEB=∠EAD,四边形ABCD是平行四边形,
∴∠ADC=∠B,
∵AE平分∠DAB,
∴∠BAE=∠EAD,
∴∠B=∠AEB=∠BAE,
∴△ABE是等边三角形,
∴∠ADC=∠B=∠BAE=∠EAD=60°,
∴∠ADE=∠ADC﹣∠EDC=60°﹣30°=30°,
∴∠AED=190°﹣60°﹣30°=90°.
4.【解答】(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°﹣80°﹣30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,
∴∠BDE=∠EDF=35°.
5.【解答】解:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
在△ABC和△AED中,
,
∴△ABC≌△EAD(SAS),
(2)∵△ABC≌△EAD,
∴∠AED=∠BAC,
∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°,
∴∠AED=85°.
6.【解答】(1)证明:∵EF垂直平分对角线BD,
∴∠DOE=∠BOF=90°,OB=OD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(AAS),
∴DE=BF,
∵EF垂直平分对角线BD,
∴DE=BE,BF=DF,
∴DE=BE=BF=DF,
∴四边形BFDE是菱形;
(2)解:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,
∵∠BOF=90°,
∴∠A=∠BOF=90°,
在Rt△BAE和Rt△BOF中,
,
∴Rt△BAE≌Rt△BOF(HL),
∴AB=OB,
∵AB=CD,OB=OD,
∴CD=BD,
∵∠C=90°,
∴∠CBD=30°,
∴∠BDC=180°﹣∠C﹣∠CBD=60°.
7.【解答】解:(1)∵在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴∠BEC=∠DFC,
∵∠BEC+∠CBE=90°,
∴∠CBE+∠DFC=90°,
∴∠BGF=90°;
(2)连接EF,
∵BE平分∠DBC,
∴∠DBG=∠CBG,
∵BG=BG,∠BGD=∠BGF=90°,
∴△BDG≌△BFG(ASA),
∴DG=FG,
∴BG垂直平分DF,
∴DE=FE,
∵CE2+CF2=EF2,CE=CF,
∴,
∴DE=CE.
8.【解答】(1)证明:∵∠ACB=∠ADB=90°,M为边AB的中点,
∴MC=AB,MD=AB,
∴MC=MD;
(2)解:∵MC=MD=AB=AM=BM,
∴∠BAC=∠ACM,∠ABD=∠BDM,
∴∠BMC=2∠BAC,∠AMD=2∠ABD,
∵△MCD是等边三角形,
∴∠DMC=60°,
∴∠BMC+∠AMD=120°,
∴2∠BAC+2∠ABD=120°,
∴∠BAO+∠ABO=60°,
∴∠AOB=180°﹣60°=120°.
9.【解答】(1)证明:∵BF=BE,CG=CE,
∴BC为△FEG的中位线,
∴BC∥FG,BC=FG,
又∵H是FG的中点,
∴FH=FG,
∴BC=FH.
又∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,
∵CE=CB,
∴∠BEC=∠EBC=75°,
∴∠BCE=180°﹣75°﹣75°=30°,
∴∠DCB=∠DCE+∠BCE=10°+30°=40°,
∴∠DAB=40°.
10.【解答】解:(1)证明:∵点B关于直线AE的对称点为F,
∴AB=AF,BE=EF,
又∵AE=AE,
∴△ABE≌△AFE(SSS),
∴∠AFE=∠B=90°,
∴AF⊥EH;
(2)连接AH,如图:
由(1)得AB=AF,AF⊥EH,
∴AF=AD,∠D=∠AFH=90°,AH=AH,
∴△AFH≌△ADH(HL),
∴∠FAH=∠DAH,
又∵∠BAE=∠FAE,在正方形ABCD中,∠BAD=90°,
∴∠EAH=45°.
长度的计算与证明(一证一求)
11.【解答】证明:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又E是AD的中点,,
∴AE∥BF,AE=BF,
∴四边形AFBE是平行四边形;
(2)过点A作AG⊥BF于G,
由?ABCD可知∠ABF=∠C=60°,
又AB=6,AD=8,
∴BG=3,FG=1,AG=,
∴BE=AF=.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠A=∠FBE,∠ADF=∠E
又∵BC=BE,
∴AD=BE,
在△ADF和△BEF中,,
∴△ADF≌△BEF(ASA);
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD=6,AD=BC,
由(1)得:△ADF≌△BEF,
∴AD=BE,EF=DF,AF=BF=AB=3,
∵AD=DB=5,
∴DB=BE=5,
∴BF⊥DE,
在Rt△BEF中,EF===4,
∴DE=2EF=2×4=8.
13.【解答】解:(1)∵E、F分别是BC、AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB且EF=AB.
又AB=2AD,即AD=AB,
∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,
∴AF与DE互相平分;
(2)∵在Rt△ABC中,∠BAC=90°,AB=8,BC=12,
∴由勾股定理得 AC===4
又由(1)知,OA=OF,且AF=CF,
∴OA=AC=.
∴在△AOD中,∠DAO=90°,AD=AB=4,OA=,
∴由勾股定理得 DO===.
14.【解答】解:(1)连接CF,
在Rt△ABC中,F是AB的中点,
∴CF=AB=5,
∵点E,F分别是边AC,AB的中点,
∴EF∥BC,EF=BC,
∵2CD=BC,
∴EF=CD,EF∥CD,
∴四边形EDCF是平行四边形,
∴DE=CF=5;
(2)如图2,∵四边形EDCF是平行四边形,
∴CF∥DM,
∵点E是边AC的中点,
∴点M是AF的中点.
15.【解答】(1)解:∵AC⊥BC,
∴∠ACB=90°,
∵AC=6,BC=8,
∴AB==10,
∵四边形ABCD是平行四边形,
∴CD=AB=10,AD∥BC
∴CA⊥AD,
∴∠CAD=90°,
∵CE=ED,
∴AE=CD=5.
(2)证明:延长AE交BC的延长线于M,在CB上取一点N,使得CN=CG,连接AN.
∵AD∥CM,
∴∠DAE=∠M,
在△DAE和△MCE中,,
∴△DAE≌△MCE(AAS),
∴AE=EM,
∵AE=ED=EC,
∴AM=CD=AB,
∵AC⊥BM,
∴BC=CM,
∵AC⊥NG,CN=CG,
∴AG=AN,
∵AG+CG=BC,
∴BN=AG=AN,
∵CB=CM,CN=CG,
∴BN=GM,
∴GA=GM,
∵AE=EM,
∴EG⊥AM,
∵FA⊥AM,
∴EG∥AF,
∵AE=EM,
∴FG=GM,
∴EG=AF,
即AF=2EG.
16.【解答】(1)解:∵∠ACB=45°,AE⊥BC,
∴∠AEC=∠AEB=90°,△ACE是等腰直角三角形,
∴∠EAC=45°,AE=CE===2,
由勾股定理得:BE===,
∴BC=BE+CE=3;
(2)证明:延长AD至G,使DG=AM,连接CG,如图所示:
∵AM=CN,
∴DG=CN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∠B=∠ADC,
∴DG∥CN,
∴四边形CGDN是平行四边形,
∴CG=DN,
∵CF⊥AB,
∴∠CFB=90°=∠AEB=∠CEA,
∴∠BAE=∠MCE,
在△ABE和△CME中,,
∴△ABE≌△CME(AAS),
∴AB=CM,∠B=∠CME,
∴CM=CD,∠CME=∠ADC,
∴∠AMC=∠GDC,
在△ACM和△GCD中,,
∴△ACM≌△GCD(SAS),
∴∠G=∠MAC=45°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴△ACG是等腰直角三角形,
∴AG=CG,
∵AG=AD+DG=AD+AM,CG=DN,
∴AD+AM=DN.
17.【解答】(1)证明:在平行四边形ABCD中,AB∥DC,
∴∠BAD+∠ADC=180°.
∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAE=∠BAE=∠BAD,∠ADF=∠CDF=∠ADC.
∴∠DAE+∠ADF=∠BAD+∠ADC=90°.
∴∠AGD=90°.
∴AE⊥DF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAF=∠AFB,
又∵∠DAF=∠BAF,
∴∠BAF=∠AFB,
∴AB=BF,
同理可得CD=CE,
∴BF=CE;
(2)解:过点C作CK∥AF交AD于K,交DE于点I,
∵AK∥FC,AF∥CK,
∴四边形AFCK是平行四边形,∠AGD=∠KID=90°,
∴AF=CK=8,
∵∠KDI+∠DKI=90°,∠DIC+∠DCI=90°,∠IDK=∠IDC,
∴∠DKI=∠DCI,
∴DK=DC=6,
∴KI=CI=4,
∵AD∥BC,
∴∠ADE=∠DEC=∠CDE,
∴CE=CD,
∵CI⊥DE,
∴EI=DI,
∵DI===2,
∴DE=2DI=4.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
19.【解答】解:(1)△ABG,△DCE是等腰三角形.
在平行四边形ABCD中,则AD∥BC,
∴∠AGB=∠GBC,
又BG平分∠ABC,
∴∠ABG=∠CBG,
∴∠ABG=∠AGB,即AB=AG,
∴△ABG是等腰三角形;
(2)由(1)可得AB=AG=CD=DE,
∴AE=DG;
(3)假设AG:GD=3:2,
∵AD=10,∴AB=AG=AD=6,
∴平行四边形的周长为2(10+6)=32;
当AG:GD=2:3时,则AB=AG=AD=4,
∴平行四边形的周长为2(10+4)=28.
所以平行四边形ABCD的周长为32或28.
