苏教版九年级下教学案 第六章《二次函数》(共12课时)
文档属性
| 名称 | 苏教版九年级下教学案 第六章《二次函数》(共12课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-25 00:00:00 | ||
图片预览




文档简介
课题 6.1 二次函数 自主空间
学习目标 知识与技能:了解二次函数关系式,会确定二次函数关系式中各项的系数。过程与方法:经历对实际问题情境分析确定二次函数表达式的过程,体会二次函数意义;情感、态度与价值观:体会二次函数是某些实际问题的数学模型
学习重点 二次函数的概念
学习难点 确定实际问题中二次函数的关系式
教学流程
预习导航 1.形如,( )的函数是一次函数,形如,( )的函数是 函数,它的表达式还可以写成: 。2.一般地,形如 ,( ,且 )的函数为二次函数。其中是自变量, 函数。一般地,二次函数中自变量的取值范围是 。
合作探究 新知探究:1.一粒石子投入水中,激起的波纹不断向外扩展,扩大的圆的面积S与半径r之间的函数关系式是 。2.用16m长的篱笆围成长方形圈养小兔,圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为 。3.要给一个边长为x (m)的正方形实验室铺设地板,已知某种地板的价格为每平方米240元,踢脚线价格为每米30元,如果其它费用为1000元,那么总费用y(元)与x(m)之间的函数关系式是 。上述函数函数关系有哪些共同之处?它们与一次函数、反比例函数的关系式有什么不同?例题分析: 例1.当k为何值时,函数为二次函数?例2.写出下列各函数关系,并判断它们是什么类型的函数.⑴圆的面积y(cm2)与它的周长x(cm)之间的函数关系;⑵某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;⑶菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.例3.已知二次函数,当时,。当时,求的值.展示交流:1.考察下列函数:①,②,③,④,⑤(是自变量)中,二次函数是: 。2.若一个边长为cm的无盖正方体形纸盒的表面积为cm,则,其中的取值范围是 。3. 如图在长200米,宽80米的矩形广场内修建等宽的十字形道路,请写出绿地面积(㎡)与路宽(m)之间的函数关系式: 。4. 如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积(㎡)与它与墙平行的边的长(m)之间的函数关系式: 。5.已知函数是二次函数,求m的值.四、提炼总结:
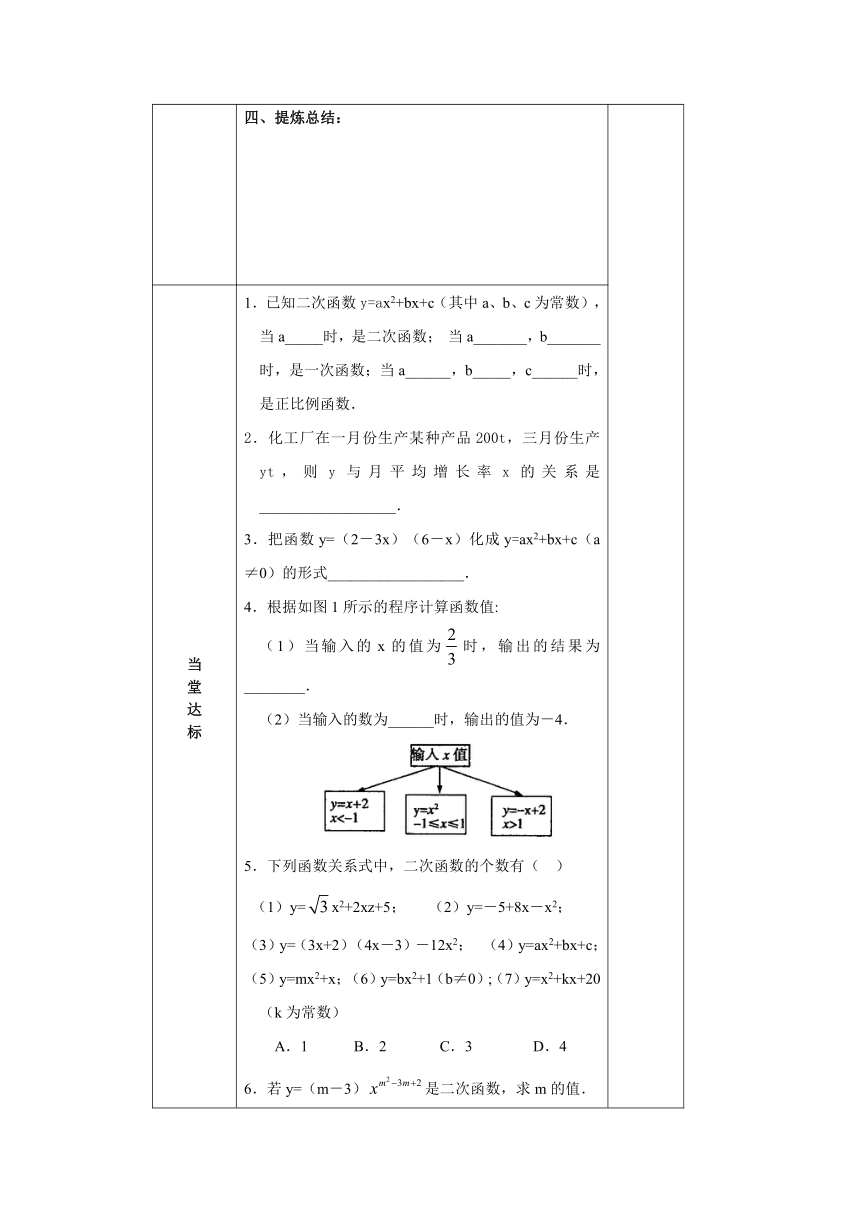
当堂达标 1.已知二次函数y=ax2+bx+c(其中a、b、c为常数),当a_____时,是二次函数;当a_______,b_______时,是一次函数;当a______,b_____,c______时,是正比例函数.2.化工厂在一月份生产某种产品200t,三月份生产yt,则y与月平均增长率x的关系是__________________.3.把函数y=(2-3x)(6-x)化成y=ax2+bx+c(a≠0)的形式__________________.4.根据如图1所示的程序计算函数值: (1)当输入的x的值为时,输出的结果为________.(2)当输入的数为______时,输出的值为-4. 5.下列函数关系式中,二次函数的个数有( ) (1)y=x2+2xz+5; (2)y=-5+8x-x2;(3)y=(3x+2)(4x-3)-12x2; (4)y=ax2+bx+c; (5)y=mx2+x;(6)y=bx2+1(b≠0);(7)y=x2+kx+20(k为常数) A.1 B.2 C.3 D.46.若y=(m-3)是二次函数,求m的值.
学习反思:
课题 §6.2 二次函数的图象和性质(1) 自主空间
学习目标 知识与技能:掌握利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.能够作出二次函数y=-x2的图象,并比较它与y=x2图象的异同,过程与方法:经历探索二次函数y=x2的图象的作法和性质的过程,获得利用图象研究二次函数性质的经验.情感、态度与价值观:初步建立二次函数表达式与图象之间的联系.
学习重点 利用描点法作出y=x2的图象过程中,理解掌握二次函数y=x2的性质,.
学习难点 函数图象的画法,及由图象概括出二次函数y=x2性质,它难在由图象概括性质,结合图象记忆性质
教学流程
预习导航 我们已经知道,一次函数,反比例函数的图象分别是 、 ,那么二次函数的图象是什么呢?它有何性质呢?
合作探究 一、新知探究:二次函数的图象是什么呢?(1)描点法画函数的图象前,想一想,列表时如何合理选值?以什么数为中心?当x取互为相反数的值时,y的值如何?(2)观察函数的图象,你能得出什么结论?二、例题分析: 在同一直角坐标系中,画出下列函数的图象。(1) (2)三、展示交流:1.在同一直角坐标系中,画出下列函数的图象。(1) (2) (3) 2.已知二次函数y=ax2经过点A(-2,4)(1)求出这个函数关系式;(2)写出抛物线上纵坐标为4的另一个点B的坐标,并求出S△AOB;(3)在抛物线上是否存在另一个点C,使得△ABC的面积等于△AOB面积的一半?如果存在,求出点C的坐标;如果不存在,请说明理由四、提炼总结:
当堂达标 1.抛物线y=ax2与y=2x2形状相同,则a= 。2.已知函数y=ax2当x=1时y=3,则a= , 对称轴是 ,顶点是 , 抛物线的开口 ,在对称轴的左侧,y随x增大而 ,当x= 时,函数y有最 值,是 .3.已知函数y=ax2的图象过点,则此图象上纵坐标为时的点的坐标为 .4.若抛物线y=ax2经过点P ( l,-2 ),则它也经过 ( ) A. P1(-1,-2 ) B. P2(-l, 2 ) C. P3( l, 2) D..P4(2, 1)5.已知a≠0,b<0,一次函数是y=ax+b,二次函数是y=ax2,则下面图中,可以成立的是( )6.有一桥孔形状是一条开口向下的抛物线 (1)作出这条抛物线; (2)利用图象,当水面与抛物线顶点的距离为4m时,求水面的宽; (3)当水面宽为6m时,水面与抛物线顶点的距离是多少?
学习反思:
课题 §6.2 二次函数的图象和性质(2) 自主空间
学习目标 知识与技能:(1)会作出y=ax2的图象,并能比较它们与y=x2的异同,理解a对二次函数图象的影响.(2)能说出y=ax2图象的开口方向、对称轴和顶点坐标.过程与方法:经历探索二次函数y=ax2的图象的作法和性质的过程,进一步获得将表格、表达式、图象三者联系起来的经验.情感、态度与价值观:体会二次函数是某些实际问题的数学模型
学习重点 二次函数y=ax2的图象和性质
学习难点 由函数图象概括出y=ax2的性质.根据函数图象联想函数性质,由性质来分析函数图象的形状和位置.
教学流程
预习导航 比较二次函数y=x2 与y=-x2和y=ax2的性质抛物线y=x2y=-x2y=ax2对称轴顶点坐标开口方向位置增减性最值
合作探究 一、新知探究:1.在同一直角坐标系中,画出下列函数的图象,并分别写出它们的开口方向、对称轴和顶点坐标.(1) (2) (3)2.总结得出二次函数y=ax2图象的性质。二、例题分析:例1.已知抛物线y=(m+1)x开口向下,求m的值.例2.已知直线y=-2x+3与抛物线y=ax2相交于A、B两点,且A点坐标为(-3,m).(1)求a、m的值;(2)求抛物线的表达式及其对称轴和顶点坐标;(3)x取何值时,二次函数y=ax2中的y随x的增大而减小;(4)求A、B两点及二次函数y=ax2的顶点构成的三角形的面积. 三、展示交流:1.(1)函数的开口 ,对称轴是 ,顶点坐标是 ;(2)函数的开口 ,对称轴是 ,顶点坐标是 .2.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( ) A.y1当堂达标 1.在同一坐标系中,抛物线y=4x2,y=x2,y=-x2的共同特点是( )A.关于y轴对称,抛物线开口向上; B.关于y轴对称,y随x的增大而增大C.关于y轴对称,y随x的增大而减小; D.关于y轴对称,抛物线顶点在原点2.下列关于抛物线y=x2和y=-x2的关系的说法错误的是( )A.它们有共同的顶点和对称轴; B.它们都关于y轴对称; C.它们的形状相同,开口方向相反; D.点A(-2,4)在抛物线y=x2上也在抛物线y=-x2上3.二次函数y=mx的图象有最高点,则m=______. 4.二次函数y=-x2,当x 1>x2>0时,则y1与y2的大小关系是_________.5.有一座抛物线形拱桥,正常水位时,桥下水面宽度为20m,拱顶距离水面4m.(1)在如图所示的直角坐标系中,求出该抛物线的表达式;(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
学习反思:
课题 6.2二次函数的图象和性质(3) 自主空间
学习目标 知识与技能:1.能够理解函数y=ax2+k(a≠0)及y=a(x+m)2 (a≠0)与y=ax2的图象的关系,理解a,m,k对二次函数图象的影响。2.正确说出函数y=ax2+k, y=a(x+m)2的图象的开口方向,顶点坐标和对称轴过程与方法:经历探索二次函数y=ax2+k(a≠0)及y=a(x+m)2 (a≠0)的图象作法和性质的过程。情感、态度与价值观:理解从特殊到一般的探索规律
学习重点 二次函数y=ax2+k, y=a(x-m)2的图象的性质
学习难点 二次函y=ax2+k 、y=a(x-m)2与y=ax2的关系的理解及应用
教学流程
预习导航 1.二次函数y=ax2的图象有哪些性质?你能列表说明吗?(提示:从开口方向,顶点坐标、对称轴、增减性、最值等方面列表)2.函数y=ax2+k的图象与函数y=ax2的图象有何关系呢?它有哪些性质?3.函数y=a(x+m)2的图象与函数y=ax2的图象有何关系呢?它有哪些性质?
合作探究 一、新知探究:1.函数y=x2+1的图象与函数y=x2的图象有何关系呢?(1)填表:x…-2-1012…y=x2…41014…y=x2+1……(2)观察:从表格中的数值看,相同自变量所对应的两个函数的函数值有何关系?(3)描点并画出函数y=x2+1的图象:(4)观察:函数y=x2+1的图象与函数y=x2的图象的位置关系?(5)归纳结论:函数y=x2+1的图象可由函数y=x2的图象________________得到,所以它的对称轴是_____,顶点坐标是_____,当x=_____时,y有最____值为_____。当x<0时,y随着x的增大而______;当x>0时,y随着x的增大而______;(6)思考:那么函数y=x2+1的图象怎样平移可得到函数y=x2的图象?2.函数y=x2-2的图象与函数y=x2的图象有何关系?3.二次函数y=ax2+k(a≠0)的图象与y=ax2 (a≠0)的图象有何关系?有哪些性质?二、例题分析: 例1.(1)函数y=4x2+5的图象可由y=4x2的图象沿y轴向 平移 个单位得到;顶点坐标是 ______;当x<0时,y随着x的增大而_______。(2)将抛物线y=-5x2沿y轴向下平移4个单位,所得的抛物线的函数式是___ ___ ___ 三、展示交流:1. 函数y=(x+3)2的图象与函数y=x2的图象有何关系?(阅读课本P14总结)函数y=(x+3) 2的图象可由函数y=x2的图象_____________得到,所以它的对称轴是_____________________,顶点坐标是_________。当x=_______时,y有最____值为_____;当x______时,y随着x的增大而增大;当x______时,y随着x的增大而减小;2.函数y=(x-3)2的图象与函数y=x2的图象有何关系?3.二次函数y=a(x+m)2 (a≠0)的图象与y=ax2 (a≠0)的图象有何关系?有哪些性质?4.(1)函数y=-2(x+3)2的图象是由y=-2x2的图象沿x轴向_____平移____个单位得到的,开口________,对称轴是_______________,顶点坐标为__________,当x=______时,y有最______值为______,当x_____时,y随着x的增大而增大。 (2)将抛物线y=5x2沿x轴向右平移3个单位,所得的抛物线的函数式是___________________,四、提炼总结:
当堂达标 1.二次函数y=-x2+2的图象可以看作抛物线y=-x2沿y轴向_____平移____个单位得到的,它的对称轴是_____,顶点坐标为________,当x=________时,y有最_____值为________,当x______时,y随着x的增大而减小。2.二次函数y=5(x-3)2的图象可由y=5x2沿x轴向_____平移____个单位得到的,开口________,对称轴是_____________________,顶点坐标为__________,当x=______时,y有最______值为______,当x________时,y随着x的增大而增大。3.二次函数y=x2的图象向右平移2个单位,得到新的图象的二次函数表达式是( ) A.y=x2-2 B.y=(x-2)2 C.y=x2+2 D.y=(x+2)24.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范 围为( ) A.m>2 B.m<2 C.0学习反思:
课题 6.2 二次函数的图象与性质(4) 自主空间
学习目标 知识与技能:1.掌握把抛物线平移至+k的规律;2.会画出+k 这类函数的图象,通过比较,了解这类函数的性质.过程与方法:经历把函数y=ax2的图象沿x轴、y轴平移排列得到函数y=a(x+h)2+k的图象的探究过程,进一步了解上述图象变换的实质是:图象的形状、大小都没有改变,只是位置发生了变化。情感、态度与价值观:渗透数学知识抽象美及图像上的形象美,提高数学美的鉴赏力。
学习重点 二次函数y=a(x+h)2+k的图象的性质
学习难点 二次函数y=a(x+h)2+k与y=ax2的本质联系
教学流程
预习导航 复习与思考:由前面的知识,我们知道,函数的图象,向 平移2个单位,可以得到函数的图象;函数的图象,向 平移3个单位,可以得到函数的图象,那么函数的图象,如何平移,才能得到函数的图象呢?
合作探究 新知探究:1.思考:(1)y=x2+2与y=x2有何关系?顶点坐标是什么?(2) y=(x+1)2与y=x2有何关系?顶点坐标是什么?(3) y=(x+1)2+2与y=x2有何关系?顶点坐标是什么?2. 探究:画函数y=x2+2x+3的图象。分析:①化为y=(x+1)2+2 ②描点法3.观察:它的开口方向 ,对称轴分别为 ,顶点坐标为. ,最值 。4.探索 你能说出函数+k(a、m、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标吗?+k开口方向对称轴顶点坐标填表:5.用配方法探索的顶点坐标公式: y= = = 即:顶点( , )例题分析: 已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)①求该函数的关系式;②求该函数图象与坐标轴的交点坐标;③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.展示交流:1.函数化成的形式是( )A. B.C. D.2.求下列抛物线的顶点坐标: (1) (2)3.二次函数的图象经过点,,.(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移 个单位,使得该图象的顶点在原点.四、提炼总结: 二次函数的图象的上下平移,只影响二次函数+k中k的值;左右平移,只影响h的值,抛物线的形状不变,所以平移时,可根据顶点坐标的改变,确定平移前、后的函数关系式及平移的路径.此外,图象的平移与平移的顺序无关.
当堂达标 1.抛物线,当y随x增大而增大时,x的取值范围是( )A.x>2 B.x<3 C.x<4 D.x>32.抛物线 。3.将抛物线平移到顶点为(2,-3),则此时的解析式为 。4.如果的最小值为2,则m的值是 。5.根据下列条件,求二次函数的关系式: (1)图象的顶点坐标是(-3,-2),并且过点(1,2)。 (2)图象与X轴相交于点M(-5,0)、N(1,0),且顶点的纵坐标是3。
学习反思:
课题 §6.3 二次函数与一元二次方程(1) 自主空间
学习目标 知识与技能:理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系。过程与方法:体会二次函数与方程之间的联系,理解一元二次方程的根就是二次函数图象与X轴交点的横坐标.情感、态度与价值观:
学习重点 本节重点把握二次函数图象与x轴交点的个数与一元二次方程的根的关系
学习难点 理解一元二次方程的根就是二次函数图象与X轴交点的横坐标.
教学流程
预习导航 在同一坐标系中画出二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象并回答下列问题:(1)每个图象与x轴有几个交点?(2)一元二次方程 x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗 (3)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
合作探究 新知探究:1.思考函数与方程有怎样的关系?例题分析: 【例1】已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为 。【例2】抛物线y=ax2+bx+c与x轴交于点A(-3,0),对称轴为x=-1,顶点C到x轴的距离为2,求此抛物线表达式.三、展示交流:1.求下列二次函数的图象与x轴交点坐标,并作草图验证.(1)y=x2-2x; (2)y=x2-2x-3.2.已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.3.你能利用a、b、c之间的某种关系判断二次函数y=ax2+bx+c的图象与x轴何时有两个交点、一个交点,何时没有交点?提炼总结:由一元二次方程ax2+bx+c=0的根的情况可以判断二次函数y=ax2+bx+c图象与x轴的交点个数。当Δ=>0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点;当Δ==0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点;当Δ=<0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点.
当堂达标 1.抛物线与轴只有一个公共点,则的值为 .2. 判断下列函数与X轴的位置关系: (1)y=2-x-x2 (2)y=-x2+6x-93.打高尔夫球时 ,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数 :y= -5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?3.有一个二次函数的图象,三位学生分别说出了它的一些特点:甲:对称轴是直线x=4;乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三点为顶点的三角形面积为3.请写出满足上述全部特点的一个二次函数表达式 .
学习反思:
课题 §6.3 二次函数与一元二次方程(2) 自主空间
学习目标 知识与技能:掌握一元二次方程及二元二次方程组的图象解法.进一步体验数形结合的数学方法。
学习重点 一元二次方程及二元二次方程组的图象解法
学习难点 一元二次方程及二元二次方程组的图象解法
教学流程
预习导航 你能求方程的解,你是如何解决的呢?我们来看一看两位同学不同的方法.甲:将方程化为,画出的图象,观察它与x轴的交点,得出方程的解.乙:分别画出函数和的图象,观察它们的交点,把交点的横坐标作为方程的解.你对这两种解法有什么看法?请与你的同学交流.
合作探究 一、新知探究:你根据函数y=x2+2x-5 的图象,求出方程x2+2x-5=0的近似根吗?你能参照上面两位同学的方法试着去解决吗?二、例题分析:利用函数的图象,求方程的解:分析 上面甲乙两位同学的解法都是可行的,但乙的方法要来得简便,因为画抛物线远比画直线困难,所以只要事先画好一条抛物线的图象,再根据待解的方程,画出相应的直线,交点的横坐标即为方程的解.解 (1)方法一:在同一直角坐标系中画出函数和的图象,如图26.3.5,得到它们的交点(-3,9)、(1,1),则方程的解为 –3,1.(2)方法二呢?三、展示交流:1.利用函数的图象,求下列方程的解:(1) (2)2.利用函数的图象,求下列方程组的解:(1); (2).四、提炼总结:一般地,求一元二次方程的近似解时,可先将方程化为,然后分别画出函数和的图象,得出交点,交点的横坐标即为方程的解.
当堂达标 1.已知二次函数y=-x2+2x+m与x轴有两个交点,其中一个交点的横坐标x1的取值范围是3学习反思:
课题 6 . 3 二次函数的运用(1) 自主空间
学习目标 体会二次函数是一类最优化问题的数学模型.了解数学的应用价值,掌握实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值、最小值.
学习重点 本节重点是应用二次函数解决实际问题中的最值.应用二次函数解决实际问题,要能正确分析和把握实际问题的数量关系,从而得到函数关系,再求最值.实际问题的最值,不仅可以帮助我们解决一些实际问题,也是中考中经常出现的一种题型.
学习难点 本节难点在于能正确理解题意,找准数量关系.这就需要同学们在平时解答此类问题时,在平时生活中注意观察和积累,使自己具备丰富的生活和数学知识才会正确分析,正确解题.
教学流程
预习导航 生活中,我们会遇到与二次函数 及其图象有关的问题。二次函数配方成y=a(x+)2+的形式时,当x= 时,y有最值= 。
合作探究 一、例题讲解:例1.将进货为40元的某种商品按50元一个售出时,能卖出500个.已知这时商品每涨价一元,其销售数就要减少20个.为了获得最大利益,售价应定为多少?例2.如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1)设矩形的一边AB=xcm,那么AD边的长度如何表示?(2)设矩形的面积为ym2,当x取何值时,y的最大值是多少 二、展示交流:1.某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与销售单价满足如下关系:在某一时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件. 请你帮助分析:销售单价是多少时,可以获利最多 2.某建筑物窗户如图所示,它的上半部是半圆,下半部是矩形.制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户透过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?三、提炼总结:能过本节学习要能正确理解题意,找准数量关系.这就需要同学们在平时解答此类问题时,在平时生活中注意观察和积累,使自己具备丰富的生活和数学知识才会正确分析,正确解题.
当堂达标 1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.问:每件衬衫降低多少元时,商场平均每天盈利最多?2.如图,已知△ABC,矩形GDEF的DE边在BC边上.G、F分别在AB、AC边上,BC=5cm,S△ABC为30cm2,AH为△ABC在BC边上的高,求△ABC的内接长方形的最大面积
学习反思:
课题 6.4二次函数的应用(2) 自主空间
学习目标 知识与技能:1.能利用二次函数解决喷水、灌溉及体育运动的问题。2.能够分析和表示实际问题中变量之间的二次函数关系过程与方法:让学生认识数学与人类生活的密切联系及对人类历史发展的作用,发展学生运用数学知识解决实际问题的能力.情感、态度与价值观:1.体会数学与人类社会的密切联系,了解数学的价值.增进对数学的理解和学好数学的信心.2.认识到数学是解决实际问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用.
学习重点 能够分析和表示实际问题中变量之间的二次函数关系
学习难点 能够分析和表示实际问题中变量之间的二次函数关系
教学流程
预习导航 1、在平原上,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=-x2+10x.(1)经过多长时间,炮弹达到它的最高点?最高点的高度是多少?(2)经过多长时间,炮弹落在地上爆炸?
合作探究 一、新知探究:1.炮弹达到它的最高点与二次函数图象的联系?2.落地时的高度是多少?二、例题分析:如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)? 三、展示交流: 橘子洲头要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.(1)求这条抛物线的解析式;(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?四、提炼总结:本节你学了哪些知识。
当堂达标 1. 体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线的一部分,根据关系式回答:⑴ 该同学的出手最大高度是多少?⑵ 铅球在运行过程中离地面的最大高度是多少?⑶ 该同学的成绩是多少?
学习反思:
课题 6.4二次函数的应用(3) 自主空间
学习目标 知识与技能:1.能利用二次函数解决抛物线拱桥及呈抛物线建筑的有关问题. 2.能够分析和表示不同背景下实际问题中变量之间的二次函数关系.过程与方法:1.通过分析和表示不同背景下实际问题中变量之间的二次函数关系,培养学生的分析判断能力.2.通过运用二次函数的知识解决实际问题,培养学生的数学应用能力情感、态度与价值观:1.能够对解决问题的基本策略进行反思,形成个人解决问题的风格.2.进一步体会数学与人类社会的密切联系,了解数学的价值.增进对数学的理解和学好数学的信心,具有初步的创新精神和实践能力.
学习重点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.
学习难点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决实际问题.
教学流程
预习导航 有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为 .
合作探究 一、新知探究:1.问题1中你能获得哪些关于抛物线的信息?2.你将设何种解析式?二、例题分析:某涵洞是抛物线形,它的截面如图26.2.9所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?三、展示交流:1.河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为 y= - x2 ,当水位线在AB位置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( ) A、5米 B、6米; C、8米; D、9米 2.当一枚火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?3.一个涵洞成抛物线形,它的截面如图现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少?是否会超过1 m?四、提炼总结:本节课你有哪些收获?
当堂达标 1.一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少 (结果精确到0.1m).2.某工厂大门是一抛物线型水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4.4m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m.请判断这辆汽车能否顺利通过大门.3.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-x2+4表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果隧道内设双行道,那么这辆货运车是否可以通过?(3)为安全起见,你认为隧道应限高多少比较适宜?为什么?
学习反思:
课题 第六章小结与思考(1) 自主空间
学习目标 知识与技能:1.知道二次函数的定义;2.知道二次函数的解析式;3.理解二次函数的图象及意义;过程与方法:1.通过解决用二次函数所表示的问题,培养学生运用能力. 2.通过对二次函数三种表示方式的特点进行研究,训练大家的求同求异思维.情感、态度与价值观:1.初步学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识.
学习重点 能够分析和表示变量之间的二次函数关系,并解决用二次函数所表示的问题.能够根据二次函数的不同表示方式,从不同的侧面对函数性质进行研究.
学习难点 能够分析和表示变量之间的二次函数关系,并解决用二次函数所表示的问题.
教学流程
预习导航 1. 二次函数的解析式:(1)一般式: ;(2)顶点: (3)交点式: . 2. 顶点式的几种特殊形式. ⑴ , ⑵ , ⑶ ,(4) . 3.二次函数通过配方可得,其抛物线关于直线 对称,顶点坐标为( , ).⑴ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当 时,有最 (“大”或“小”)值是 ;⑵ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当 时,有最 (“大”或“小”)值是
合作探究 例题分析:【例1】二次函数y=ax2+bx2+c的图象如图所示,则a 0,b 0,c 0(填“>”或“<”=.)【例2】二次函数y=ax2+bx+c与一次函数y=ax+c在同一坐标系中的图象大致是图中的( )【例3】在同一坐标系中,函数y=ax2+bx与y=的图象大致是图中的( )【例4】如图所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称,你能写出右面钢缆的表达式吗?【例5】抛物线y=ax2+bx+c如图所示,则它关于y轴对称的抛物线的表达式是 .【例6】已知二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5).(1)求m的值,并写出二次函数的表达式;(2)求出二次函数图象的顶点坐标、对称轴.1.抛物线y=-2x2+6x-1的顶点坐标为 ,对称轴为 .2.如果一条抛物线与抛物线y=-x2+2的形状相同,且顶点坐标是(4,-2),则它的表达式是 .3.抛物线y=3x2-2向左平移2个单位,向下平移3个单位,则所得抛物线为( )A.y=3(x+2)2+1 B.y=3(x-2)2-1C.y=3(x+2)2-5 D.y=3(x-2)2-24.如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面 内的点,则点P在( )6.抛物线y=2x2向左平移1个单位,再向下平移3个单位,得到 的抛物线表达式为 .7.如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )A.abc>0 B.a+b+c<0 C.b<a+c D.2c<3b8.如图,已知二次函数y=x2+bx+c,图象过A(-3,6),并与x轴交于B(-1,0)和点C,顶点为P.(1)求这个二次函数表达式;(2)设D为线段OC上的一点,且满足∠DPC=∠BAC,求D点坐标.
学习反思:
课题 第六章小结与思考(2) 自主空间
学习目标 知识与技能:进一步获得利用数学方法解决实际问题的经验,并进一步感受数学模型思想和数学的应用价值.过程与方法:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.情感、态度与价值观:1.学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识.
学习重点 能够运用二次函数的知识解决实际问题.
学习难点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决实际问题.
教学流程
预习导航 某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日生产的产品全部售出.已知生产x只玩具熊猫的成本为R(元),每只售价为P(元),且R,P与x的表达式分别为R=500+30x,P=170-2x.(1)当日产量为多少时,每日获利为1750元?(2)当日产量为多少时,可获得最大利润?最大利润是多少?
合作探究 一.例题分析:【例1】启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量为10万件.为了获得更好的利益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且y=-+x+,如果把利润看作是销售总额减去成本费和广告费.(1)试写出年利润S(万元)与广告费x(万元)的函数表达式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?(2)把(1)中的最大利润留出3万元作广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:项目ABCDEF每股(万元)526468收益(万元)0.550.40.60.50.91如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元,问有几种符合要求的投资方式?写出每种投资方式所选的项目.【例2】已知抛物线y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x+1的顶点是B(如图).(1)判断点A是否在抛物线y=x2-2x+1上,为什么?(2)如果抛物线y=a(x-t-1)2+t2经过点B.①求a的值;②这条抛物线与x轴的两个交点和它的顶点A能否成直角三角形?若能,求出t的值;若不能,请说明理由.【例3】如图,E、F分别是边长为4的正方形ABCD的边BC、CD上的点,CE=1,CF=,直线FE交AB的延长线于G,过线段FG上的一个动点H,作HM⊥AG于M.设HM=x,矩形AMHN的面积为y.(1)求y与x之间的函数表达式,(2)当x为何值时,矩形AMHN的面积最大,最大面积是多少?当堂练习:1.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单位每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数表达式(不必写出x的取值范围);(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少? 2.已知:如图,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.若△A′B′C′与△ABC完全重合,令△ABC固定不动,将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动.设移动xs后,△A′B′C′与△ABC的重叠部分的面积为ycm2.求:(1)y与x之间的函数关系;(2)几秒钟后两个三角形重叠部分的面积等于cm2?
学习反思:
参考答案:
6.1 二次函数
1.;=0,;=0,,=0; 2.;3.
4.(1);(2)6或-6;5.C;6.0
6.2 二次函数的图象和性质(1)
1.2; 2.3,y轴,(0,0),向上,减小,0,小,0;3.
4.A; 5.C;6.(1)略,(2)8,(3)
6.2 二次函数的图象和性质(2)
1.D; 2.D;3.-2;4.y16.2 二次函数的图象和性质(3)
1.上,2,y轴,(0,2);0,大,2,>0; 2.右,3,上,过点(3,0)平行于y轴的直线,(3,0),3,小,0,>3;3.B;4.C; 5.B
6.2二次函数的图象与性质(4)
1.D 2. (1,1) 3. y=3(x-2)2-3 4. 5. y= ; y=
6.3 二次函数与一元二次方程(1)
1. 8 2. 4百米 ;不能 3. 答案不唯一。
6.3二次函数与一元二次方程(2)
1.6.4 二次函数的运用(1)
1.Y= , 降低15元。
2.S= , y=15.
6.4 二次函数的运用(2)
1. (1)2 (2)5 (3)6+2
6.4 二次函数的运用(3)
1. 4.9 2.不能 3. (1)能 (2)能(3)5米
第六章 小结与思考(1)
1.( ),直线X= 2. 3.C 4.D 5.第四象限
y(米)
4
1
2
3
A
0
10
X
学习目标 知识与技能:了解二次函数关系式,会确定二次函数关系式中各项的系数。过程与方法:经历对实际问题情境分析确定二次函数表达式的过程,体会二次函数意义;情感、态度与价值观:体会二次函数是某些实际问题的数学模型
学习重点 二次函数的概念
学习难点 确定实际问题中二次函数的关系式
教学流程
预习导航 1.形如,( )的函数是一次函数,形如,( )的函数是 函数,它的表达式还可以写成: 。2.一般地,形如 ,( ,且 )的函数为二次函数。其中是自变量, 函数。一般地,二次函数中自变量的取值范围是 。
合作探究 新知探究:1.一粒石子投入水中,激起的波纹不断向外扩展,扩大的圆的面积S与半径r之间的函数关系式是 。2.用16m长的篱笆围成长方形圈养小兔,圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为 。3.要给一个边长为x (m)的正方形实验室铺设地板,已知某种地板的价格为每平方米240元,踢脚线价格为每米30元,如果其它费用为1000元,那么总费用y(元)与x(m)之间的函数关系式是 。上述函数函数关系有哪些共同之处?它们与一次函数、反比例函数的关系式有什么不同?例题分析: 例1.当k为何值时,函数为二次函数?例2.写出下列各函数关系,并判断它们是什么类型的函数.⑴圆的面积y(cm2)与它的周长x(cm)之间的函数关系;⑵某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;⑶菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.例3.已知二次函数,当时,。当时,求的值.展示交流:1.考察下列函数:①,②,③,④,⑤(是自变量)中,二次函数是: 。2.若一个边长为cm的无盖正方体形纸盒的表面积为cm,则,其中的取值范围是 。3. 如图在长200米,宽80米的矩形广场内修建等宽的十字形道路,请写出绿地面积(㎡)与路宽(m)之间的函数关系式: 。4. 如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积(㎡)与它与墙平行的边的长(m)之间的函数关系式: 。5.已知函数是二次函数,求m的值.四、提炼总结:
当堂达标 1.已知二次函数y=ax2+bx+c(其中a、b、c为常数),当a_____时,是二次函数;当a_______,b_______时,是一次函数;当a______,b_____,c______时,是正比例函数.2.化工厂在一月份生产某种产品200t,三月份生产yt,则y与月平均增长率x的关系是__________________.3.把函数y=(2-3x)(6-x)化成y=ax2+bx+c(a≠0)的形式__________________.4.根据如图1所示的程序计算函数值: (1)当输入的x的值为时,输出的结果为________.(2)当输入的数为______时,输出的值为-4. 5.下列函数关系式中,二次函数的个数有( ) (1)y=x2+2xz+5; (2)y=-5+8x-x2;(3)y=(3x+2)(4x-3)-12x2; (4)y=ax2+bx+c; (5)y=mx2+x;(6)y=bx2+1(b≠0);(7)y=x2+kx+20(k为常数) A.1 B.2 C.3 D.46.若y=(m-3)是二次函数,求m的值.
学习反思:
课题 §6.2 二次函数的图象和性质(1) 自主空间
学习目标 知识与技能:掌握利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.能够作出二次函数y=-x2的图象,并比较它与y=x2图象的异同,过程与方法:经历探索二次函数y=x2的图象的作法和性质的过程,获得利用图象研究二次函数性质的经验.情感、态度与价值观:初步建立二次函数表达式与图象之间的联系.
学习重点 利用描点法作出y=x2的图象过程中,理解掌握二次函数y=x2的性质,.
学习难点 函数图象的画法,及由图象概括出二次函数y=x2性质,它难在由图象概括性质,结合图象记忆性质
教学流程
预习导航 我们已经知道,一次函数,反比例函数的图象分别是 、 ,那么二次函数的图象是什么呢?它有何性质呢?
合作探究 一、新知探究:二次函数的图象是什么呢?(1)描点法画函数的图象前,想一想,列表时如何合理选值?以什么数为中心?当x取互为相反数的值时,y的值如何?(2)观察函数的图象,你能得出什么结论?二、例题分析: 在同一直角坐标系中,画出下列函数的图象。(1) (2)三、展示交流:1.在同一直角坐标系中,画出下列函数的图象。(1) (2) (3) 2.已知二次函数y=ax2经过点A(-2,4)(1)求出这个函数关系式;(2)写出抛物线上纵坐标为4的另一个点B的坐标,并求出S△AOB;(3)在抛物线上是否存在另一个点C,使得△ABC的面积等于△AOB面积的一半?如果存在,求出点C的坐标;如果不存在,请说明理由四、提炼总结:
当堂达标 1.抛物线y=ax2与y=2x2形状相同,则a= 。2.已知函数y=ax2当x=1时y=3,则a= , 对称轴是 ,顶点是 , 抛物线的开口 ,在对称轴的左侧,y随x增大而 ,当x= 时,函数y有最 值,是 .3.已知函数y=ax2的图象过点,则此图象上纵坐标为时的点的坐标为 .4.若抛物线y=ax2经过点P ( l,-2 ),则它也经过 ( ) A. P1(-1,-2 ) B. P2(-l, 2 ) C. P3( l, 2) D..P4(2, 1)5.已知a≠0,b<0,一次函数是y=ax+b,二次函数是y=ax2,则下面图中,可以成立的是( )6.有一桥孔形状是一条开口向下的抛物线 (1)作出这条抛物线; (2)利用图象,当水面与抛物线顶点的距离为4m时,求水面的宽; (3)当水面宽为6m时,水面与抛物线顶点的距离是多少?
学习反思:
课题 §6.2 二次函数的图象和性质(2) 自主空间
学习目标 知识与技能:(1)会作出y=ax2的图象,并能比较它们与y=x2的异同,理解a对二次函数图象的影响.(2)能说出y=ax2图象的开口方向、对称轴和顶点坐标.过程与方法:经历探索二次函数y=ax2的图象的作法和性质的过程,进一步获得将表格、表达式、图象三者联系起来的经验.情感、态度与价值观:体会二次函数是某些实际问题的数学模型
学习重点 二次函数y=ax2的图象和性质
学习难点 由函数图象概括出y=ax2的性质.根据函数图象联想函数性质,由性质来分析函数图象的形状和位置.
教学流程
预习导航 比较二次函数y=x2 与y=-x2和y=ax2的性质抛物线y=x2y=-x2y=ax2对称轴顶点坐标开口方向位置增减性最值
合作探究 一、新知探究:1.在同一直角坐标系中,画出下列函数的图象,并分别写出它们的开口方向、对称轴和顶点坐标.(1) (2) (3)2.总结得出二次函数y=ax2图象的性质。二、例题分析:例1.已知抛物线y=(m+1)x开口向下,求m的值.例2.已知直线y=-2x+3与抛物线y=ax2相交于A、B两点,且A点坐标为(-3,m).(1)求a、m的值;(2)求抛物线的表达式及其对称轴和顶点坐标;(3)x取何值时,二次函数y=ax2中的y随x的增大而减小;(4)求A、B两点及二次函数y=ax2的顶点构成的三角形的面积. 三、展示交流:1.(1)函数的开口 ,对称轴是 ,顶点坐标是 ;(2)函数的开口 ,对称轴是 ,顶点坐标是 .2.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( ) A.y1
学习反思:
课题 6.2二次函数的图象和性质(3) 自主空间
学习目标 知识与技能:1.能够理解函数y=ax2+k(a≠0)及y=a(x+m)2 (a≠0)与y=ax2的图象的关系,理解a,m,k对二次函数图象的影响。2.正确说出函数y=ax2+k, y=a(x+m)2的图象的开口方向,顶点坐标和对称轴过程与方法:经历探索二次函数y=ax2+k(a≠0)及y=a(x+m)2 (a≠0)的图象作法和性质的过程。情感、态度与价值观:理解从特殊到一般的探索规律
学习重点 二次函数y=ax2+k, y=a(x-m)2的图象的性质
学习难点 二次函y=ax2+k 、y=a(x-m)2与y=ax2的关系的理解及应用
教学流程
预习导航 1.二次函数y=ax2的图象有哪些性质?你能列表说明吗?(提示:从开口方向,顶点坐标、对称轴、增减性、最值等方面列表)2.函数y=ax2+k的图象与函数y=ax2的图象有何关系呢?它有哪些性质?3.函数y=a(x+m)2的图象与函数y=ax2的图象有何关系呢?它有哪些性质?
合作探究 一、新知探究:1.函数y=x2+1的图象与函数y=x2的图象有何关系呢?(1)填表:x…-2-1012…y=x2…41014…y=x2+1……(2)观察:从表格中的数值看,相同自变量所对应的两个函数的函数值有何关系?(3)描点并画出函数y=x2+1的图象:(4)观察:函数y=x2+1的图象与函数y=x2的图象的位置关系?(5)归纳结论:函数y=x2+1的图象可由函数y=x2的图象________________得到,所以它的对称轴是_____,顶点坐标是_____,当x=_____时,y有最____值为_____。当x<0时,y随着x的增大而______;当x>0时,y随着x的增大而______;(6)思考:那么函数y=x2+1的图象怎样平移可得到函数y=x2的图象?2.函数y=x2-2的图象与函数y=x2的图象有何关系?3.二次函数y=ax2+k(a≠0)的图象与y=ax2 (a≠0)的图象有何关系?有哪些性质?二、例题分析: 例1.(1)函数y=4x2+5的图象可由y=4x2的图象沿y轴向 平移 个单位得到;顶点坐标是 ______;当x<0时,y随着x的增大而_______。(2)将抛物线y=-5x2沿y轴向下平移4个单位,所得的抛物线的函数式是___ ___ ___ 三、展示交流:1. 函数y=(x+3)2的图象与函数y=x2的图象有何关系?(阅读课本P14总结)函数y=(x+3) 2的图象可由函数y=x2的图象_____________得到,所以它的对称轴是_____________________,顶点坐标是_________。当x=_______时,y有最____值为_____;当x______时,y随着x的增大而增大;当x______时,y随着x的增大而减小;2.函数y=(x-3)2的图象与函数y=x2的图象有何关系?3.二次函数y=a(x+m)2 (a≠0)的图象与y=ax2 (a≠0)的图象有何关系?有哪些性质?4.(1)函数y=-2(x+3)2的图象是由y=-2x2的图象沿x轴向_____平移____个单位得到的,开口________,对称轴是_______________,顶点坐标为__________,当x=______时,y有最______值为______,当x_____时,y随着x的增大而增大。 (2)将抛物线y=5x2沿x轴向右平移3个单位,所得的抛物线的函数式是___________________,四、提炼总结:
当堂达标 1.二次函数y=-x2+2的图象可以看作抛物线y=-x2沿y轴向_____平移____个单位得到的,它的对称轴是_____,顶点坐标为________,当x=________时,y有最_____值为________,当x______时,y随着x的增大而减小。2.二次函数y=5(x-3)2的图象可由y=5x2沿x轴向_____平移____个单位得到的,开口________,对称轴是_____________________,顶点坐标为__________,当x=______时,y有最______值为______,当x________时,y随着x的增大而增大。3.二次函数y=x2的图象向右平移2个单位,得到新的图象的二次函数表达式是( ) A.y=x2-2 B.y=(x-2)2 C.y=x2+2 D.y=(x+2)24.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范 围为( ) A.m>2 B.m<2 C.0
课题 6.2 二次函数的图象与性质(4) 自主空间
学习目标 知识与技能:1.掌握把抛物线平移至+k的规律;2.会画出+k 这类函数的图象,通过比较,了解这类函数的性质.过程与方法:经历把函数y=ax2的图象沿x轴、y轴平移排列得到函数y=a(x+h)2+k的图象的探究过程,进一步了解上述图象变换的实质是:图象的形状、大小都没有改变,只是位置发生了变化。情感、态度与价值观:渗透数学知识抽象美及图像上的形象美,提高数学美的鉴赏力。
学习重点 二次函数y=a(x+h)2+k的图象的性质
学习难点 二次函数y=a(x+h)2+k与y=ax2的本质联系
教学流程
预习导航 复习与思考:由前面的知识,我们知道,函数的图象,向 平移2个单位,可以得到函数的图象;函数的图象,向 平移3个单位,可以得到函数的图象,那么函数的图象,如何平移,才能得到函数的图象呢?
合作探究 新知探究:1.思考:(1)y=x2+2与y=x2有何关系?顶点坐标是什么?(2) y=(x+1)2与y=x2有何关系?顶点坐标是什么?(3) y=(x+1)2+2与y=x2有何关系?顶点坐标是什么?2. 探究:画函数y=x2+2x+3的图象。分析:①化为y=(x+1)2+2 ②描点法3.观察:它的开口方向 ,对称轴分别为 ,顶点坐标为. ,最值 。4.探索 你能说出函数+k(a、m、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标吗?+k开口方向对称轴顶点坐标填表:5.用配方法探索的顶点坐标公式: y= = = 即:顶点( , )例题分析: 已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)①求该函数的关系式;②求该函数图象与坐标轴的交点坐标;③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.展示交流:1.函数化成的形式是( )A. B.C. D.2.求下列抛物线的顶点坐标: (1) (2)3.二次函数的图象经过点,,.(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移 个单位,使得该图象的顶点在原点.四、提炼总结: 二次函数的图象的上下平移,只影响二次函数+k中k的值;左右平移,只影响h的值,抛物线的形状不变,所以平移时,可根据顶点坐标的改变,确定平移前、后的函数关系式及平移的路径.此外,图象的平移与平移的顺序无关.
当堂达标 1.抛物线,当y随x增大而增大时,x的取值范围是( )A.x>2 B.x<3 C.x<4 D.x>32.抛物线 。3.将抛物线平移到顶点为(2,-3),则此时的解析式为 。4.如果的最小值为2,则m的值是 。5.根据下列条件,求二次函数的关系式: (1)图象的顶点坐标是(-3,-2),并且过点(1,2)。 (2)图象与X轴相交于点M(-5,0)、N(1,0),且顶点的纵坐标是3。
学习反思:
课题 §6.3 二次函数与一元二次方程(1) 自主空间
学习目标 知识与技能:理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系。过程与方法:体会二次函数与方程之间的联系,理解一元二次方程的根就是二次函数图象与X轴交点的横坐标.情感、态度与价值观:
学习重点 本节重点把握二次函数图象与x轴交点的个数与一元二次方程的根的关系
学习难点 理解一元二次方程的根就是二次函数图象与X轴交点的横坐标.
教学流程
预习导航 在同一坐标系中画出二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象并回答下列问题:(1)每个图象与x轴有几个交点?(2)一元二次方程 x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗 (3)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
合作探究 新知探究:1.思考函数与方程有怎样的关系?例题分析: 【例1】已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为 。【例2】抛物线y=ax2+bx+c与x轴交于点A(-3,0),对称轴为x=-1,顶点C到x轴的距离为2,求此抛物线表达式.三、展示交流:1.求下列二次函数的图象与x轴交点坐标,并作草图验证.(1)y=x2-2x; (2)y=x2-2x-3.2.已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.3.你能利用a、b、c之间的某种关系判断二次函数y=ax2+bx+c的图象与x轴何时有两个交点、一个交点,何时没有交点?提炼总结:由一元二次方程ax2+bx+c=0的根的情况可以判断二次函数y=ax2+bx+c图象与x轴的交点个数。当Δ=>0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点;当Δ==0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点;当Δ=<0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点.
当堂达标 1.抛物线与轴只有一个公共点,则的值为 .2. 判断下列函数与X轴的位置关系: (1)y=2-x-x2 (2)y=-x2+6x-93.打高尔夫球时 ,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数 :y= -5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?3.有一个二次函数的图象,三位学生分别说出了它的一些特点:甲:对称轴是直线x=4;乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三点为顶点的三角形面积为3.请写出满足上述全部特点的一个二次函数表达式 .
学习反思:
课题 §6.3 二次函数与一元二次方程(2) 自主空间
学习目标 知识与技能:掌握一元二次方程及二元二次方程组的图象解法.进一步体验数形结合的数学方法。
学习重点 一元二次方程及二元二次方程组的图象解法
学习难点 一元二次方程及二元二次方程组的图象解法
教学流程
预习导航 你能求方程的解,你是如何解决的呢?我们来看一看两位同学不同的方法.甲:将方程化为,画出的图象,观察它与x轴的交点,得出方程的解.乙:分别画出函数和的图象,观察它们的交点,把交点的横坐标作为方程的解.你对这两种解法有什么看法?请与你的同学交流.
合作探究 一、新知探究:你根据函数y=x2+2x-5 的图象,求出方程x2+2x-5=0的近似根吗?你能参照上面两位同学的方法试着去解决吗?二、例题分析:利用函数的图象,求方程的解:分析 上面甲乙两位同学的解法都是可行的,但乙的方法要来得简便,因为画抛物线远比画直线困难,所以只要事先画好一条抛物线的图象,再根据待解的方程,画出相应的直线,交点的横坐标即为方程的解.解 (1)方法一:在同一直角坐标系中画出函数和的图象,如图26.3.5,得到它们的交点(-3,9)、(1,1),则方程的解为 –3,1.(2)方法二呢?三、展示交流:1.利用函数的图象,求下列方程的解:(1) (2)2.利用函数的图象,求下列方程组的解:(1); (2).四、提炼总结:一般地,求一元二次方程的近似解时,可先将方程化为,然后分别画出函数和的图象,得出交点,交点的横坐标即为方程的解.
当堂达标 1.已知二次函数y=-x2+2x+m与x轴有两个交点,其中一个交点的横坐标x1的取值范围是3
课题 6 . 3 二次函数的运用(1) 自主空间
学习目标 体会二次函数是一类最优化问题的数学模型.了解数学的应用价值,掌握实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值、最小值.
学习重点 本节重点是应用二次函数解决实际问题中的最值.应用二次函数解决实际问题,要能正确分析和把握实际问题的数量关系,从而得到函数关系,再求最值.实际问题的最值,不仅可以帮助我们解决一些实际问题,也是中考中经常出现的一种题型.
学习难点 本节难点在于能正确理解题意,找准数量关系.这就需要同学们在平时解答此类问题时,在平时生活中注意观察和积累,使自己具备丰富的生活和数学知识才会正确分析,正确解题.
教学流程
预习导航 生活中,我们会遇到与二次函数 及其图象有关的问题。二次函数配方成y=a(x+)2+的形式时,当x= 时,y有最值= 。
合作探究 一、例题讲解:例1.将进货为40元的某种商品按50元一个售出时,能卖出500个.已知这时商品每涨价一元,其销售数就要减少20个.为了获得最大利益,售价应定为多少?例2.如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1)设矩形的一边AB=xcm,那么AD边的长度如何表示?(2)设矩形的面积为ym2,当x取何值时,y的最大值是多少 二、展示交流:1.某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与销售单价满足如下关系:在某一时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件. 请你帮助分析:销售单价是多少时,可以获利最多 2.某建筑物窗户如图所示,它的上半部是半圆,下半部是矩形.制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户透过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?三、提炼总结:能过本节学习要能正确理解题意,找准数量关系.这就需要同学们在平时解答此类问题时,在平时生活中注意观察和积累,使自己具备丰富的生活和数学知识才会正确分析,正确解题.
当堂达标 1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.问:每件衬衫降低多少元时,商场平均每天盈利最多?2.如图,已知△ABC,矩形GDEF的DE边在BC边上.G、F分别在AB、AC边上,BC=5cm,S△ABC为30cm2,AH为△ABC在BC边上的高,求△ABC的内接长方形的最大面积
学习反思:
课题 6.4二次函数的应用(2) 自主空间
学习目标 知识与技能:1.能利用二次函数解决喷水、灌溉及体育运动的问题。2.能够分析和表示实际问题中变量之间的二次函数关系过程与方法:让学生认识数学与人类生活的密切联系及对人类历史发展的作用,发展学生运用数学知识解决实际问题的能力.情感、态度与价值观:1.体会数学与人类社会的密切联系,了解数学的价值.增进对数学的理解和学好数学的信心.2.认识到数学是解决实际问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用.
学习重点 能够分析和表示实际问题中变量之间的二次函数关系
学习难点 能够分析和表示实际问题中变量之间的二次函数关系
教学流程
预习导航 1、在平原上,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=-x2+10x.(1)经过多长时间,炮弹达到它的最高点?最高点的高度是多少?(2)经过多长时间,炮弹落在地上爆炸?
合作探究 一、新知探究:1.炮弹达到它的最高点与二次函数图象的联系?2.落地时的高度是多少?二、例题分析:如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)? 三、展示交流: 橘子洲头要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.(1)求这条抛物线的解析式;(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?四、提炼总结:本节你学了哪些知识。
当堂达标 1. 体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线的一部分,根据关系式回答:⑴ 该同学的出手最大高度是多少?⑵ 铅球在运行过程中离地面的最大高度是多少?⑶ 该同学的成绩是多少?
学习反思:
课题 6.4二次函数的应用(3) 自主空间
学习目标 知识与技能:1.能利用二次函数解决抛物线拱桥及呈抛物线建筑的有关问题. 2.能够分析和表示不同背景下实际问题中变量之间的二次函数关系.过程与方法:1.通过分析和表示不同背景下实际问题中变量之间的二次函数关系,培养学生的分析判断能力.2.通过运用二次函数的知识解决实际问题,培养学生的数学应用能力情感、态度与价值观:1.能够对解决问题的基本策略进行反思,形成个人解决问题的风格.2.进一步体会数学与人类社会的密切联系,了解数学的价值.增进对数学的理解和学好数学的信心,具有初步的创新精神和实践能力.
学习重点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.
学习难点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决实际问题.
教学流程
预习导航 有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为 .
合作探究 一、新知探究:1.问题1中你能获得哪些关于抛物线的信息?2.你将设何种解析式?二、例题分析:某涵洞是抛物线形,它的截面如图26.2.9所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?三、展示交流:1.河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为 y= - x2 ,当水位线在AB位置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( ) A、5米 B、6米; C、8米; D、9米 2.当一枚火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?3.一个涵洞成抛物线形,它的截面如图现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少?是否会超过1 m?四、提炼总结:本节课你有哪些收获?
当堂达标 1.一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少 (结果精确到0.1m).2.某工厂大门是一抛物线型水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4.4m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m.请判断这辆汽车能否顺利通过大门.3.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-x2+4表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果隧道内设双行道,那么这辆货运车是否可以通过?(3)为安全起见,你认为隧道应限高多少比较适宜?为什么?
学习反思:
课题 第六章小结与思考(1) 自主空间
学习目标 知识与技能:1.知道二次函数的定义;2.知道二次函数的解析式;3.理解二次函数的图象及意义;过程与方法:1.通过解决用二次函数所表示的问题,培养学生运用能力. 2.通过对二次函数三种表示方式的特点进行研究,训练大家的求同求异思维.情感、态度与价值观:1.初步学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识.
学习重点 能够分析和表示变量之间的二次函数关系,并解决用二次函数所表示的问题.能够根据二次函数的不同表示方式,从不同的侧面对函数性质进行研究.
学习难点 能够分析和表示变量之间的二次函数关系,并解决用二次函数所表示的问题.
教学流程
预习导航 1. 二次函数的解析式:(1)一般式: ;(2)顶点: (3)交点式: . 2. 顶点式的几种特殊形式. ⑴ , ⑵ , ⑶ ,(4) . 3.二次函数通过配方可得,其抛物线关于直线 对称,顶点坐标为( , ).⑴ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当 时,有最 (“大”或“小”)值是 ;⑵ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当 时,有最 (“大”或“小”)值是
合作探究 例题分析:【例1】二次函数y=ax2+bx2+c的图象如图所示,则a 0,b 0,c 0(填“>”或“<”=.)【例2】二次函数y=ax2+bx+c与一次函数y=ax+c在同一坐标系中的图象大致是图中的( )【例3】在同一坐标系中,函数y=ax2+bx与y=的图象大致是图中的( )【例4】如图所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称,你能写出右面钢缆的表达式吗?【例5】抛物线y=ax2+bx+c如图所示,则它关于y轴对称的抛物线的表达式是 .【例6】已知二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5).(1)求m的值,并写出二次函数的表达式;(2)求出二次函数图象的顶点坐标、对称轴.1.抛物线y=-2x2+6x-1的顶点坐标为 ,对称轴为 .2.如果一条抛物线与抛物线y=-x2+2的形状相同,且顶点坐标是(4,-2),则它的表达式是 .3.抛物线y=3x2-2向左平移2个单位,向下平移3个单位,则所得抛物线为( )A.y=3(x+2)2+1 B.y=3(x-2)2-1C.y=3(x+2)2-5 D.y=3(x-2)2-24.如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面 内的点,则点P在( )6.抛物线y=2x2向左平移1个单位,再向下平移3个单位,得到 的抛物线表达式为 .7.如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )A.abc>0 B.a+b+c<0 C.b<a+c D.2c<3b8.如图,已知二次函数y=x2+bx+c,图象过A(-3,6),并与x轴交于B(-1,0)和点C,顶点为P.(1)求这个二次函数表达式;(2)设D为线段OC上的一点,且满足∠DPC=∠BAC,求D点坐标.
学习反思:
课题 第六章小结与思考(2) 自主空间
学习目标 知识与技能:进一步获得利用数学方法解决实际问题的经验,并进一步感受数学模型思想和数学的应用价值.过程与方法:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.情感、态度与价值观:1.学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识.
学习重点 能够运用二次函数的知识解决实际问题.
学习难点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决实际问题.
教学流程
预习导航 某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日生产的产品全部售出.已知生产x只玩具熊猫的成本为R(元),每只售价为P(元),且R,P与x的表达式分别为R=500+30x,P=170-2x.(1)当日产量为多少时,每日获利为1750元?(2)当日产量为多少时,可获得最大利润?最大利润是多少?
合作探究 一.例题分析:【例1】启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量为10万件.为了获得更好的利益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且y=-+x+,如果把利润看作是销售总额减去成本费和广告费.(1)试写出年利润S(万元)与广告费x(万元)的函数表达式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?(2)把(1)中的最大利润留出3万元作广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:项目ABCDEF每股(万元)526468收益(万元)0.550.40.60.50.91如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元,问有几种符合要求的投资方式?写出每种投资方式所选的项目.【例2】已知抛物线y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x+1的顶点是B(如图).(1)判断点A是否在抛物线y=x2-2x+1上,为什么?(2)如果抛物线y=a(x-t-1)2+t2经过点B.①求a的值;②这条抛物线与x轴的两个交点和它的顶点A能否成直角三角形?若能,求出t的值;若不能,请说明理由.【例3】如图,E、F分别是边长为4的正方形ABCD的边BC、CD上的点,CE=1,CF=,直线FE交AB的延长线于G,过线段FG上的一个动点H,作HM⊥AG于M.设HM=x,矩形AMHN的面积为y.(1)求y与x之间的函数表达式,(2)当x为何值时,矩形AMHN的面积最大,最大面积是多少?当堂练习:1.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单位每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数表达式(不必写出x的取值范围);(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少? 2.已知:如图,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.若△A′B′C′与△ABC完全重合,令△ABC固定不动,将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动.设移动xs后,△A′B′C′与△ABC的重叠部分的面积为ycm2.求:(1)y与x之间的函数关系;(2)几秒钟后两个三角形重叠部分的面积等于cm2?
学习反思:
参考答案:
6.1 二次函数
1.;=0,;=0,,=0; 2.;3.
4.(1);(2)6或-6;5.C;6.0
6.2 二次函数的图象和性质(1)
1.2; 2.3,y轴,(0,0),向上,减小,0,小,0;3.
4.A; 5.C;6.(1)略,(2)8,(3)
6.2 二次函数的图象和性质(2)
1.D; 2.D;3.-2;4.y1
1.上,2,y轴,(0,2);0,大,2,>0; 2.右,3,上,过点(3,0)平行于y轴的直线,(3,0),3,小,0,>3;3.B;4.C; 5.B
6.2二次函数的图象与性质(4)
1.D 2. (1,1) 3. y=3(x-2)2-3 4. 5. y= ; y=
6.3 二次函数与一元二次方程(1)
1. 8 2. 4百米 ;不能 3. 答案不唯一。
6.3二次函数与一元二次方程(2)
1.
1.Y= , 降低15元。
2.S= , y=15.
6.4 二次函数的运用(2)
1. (1)2 (2)5 (3)6+2
6.4 二次函数的运用(3)
1. 4.9 2.不能 3. (1)能 (2)能(3)5米
第六章 小结与思考(1)
1.( ),直线X= 2. 3.C 4.D 5.第四象限
y(米)
4
1
2
3
A
0
10
X
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
