苏教版九年级下教学案 第九章《概率的简单应用》(共3课时)
文档属性
| 名称 | 苏教版九年级下教学案 第九章《概率的简单应用》(共3课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 48.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-25 00:00:00 | ||
图片预览




文档简介
课题 9.1抽签的方法合理吗 自主空间
学习目标 1.让学生经历抽签的探索过程,感受抽签方法2.通过探索,由学生总结“先抽的人与后抽的人”中签的概率是否一样3.探索和经验总结,抽签的方法是合理的
学习重点 通过探索,得出“先抽的人与后抽的人”中签的概率一样
学习难点 探索和经验总结,抽签的方法是合理的
教学流程
预习导航 有一张电影票,小明和小丽用抽签的方法来决定谁可以去看电影,于是准备了两张相同的小纸条,一张上面是“去”,另一张上面是“不去”,谁抽到“去”,则这个人就去看电影,这种方法公平吗?
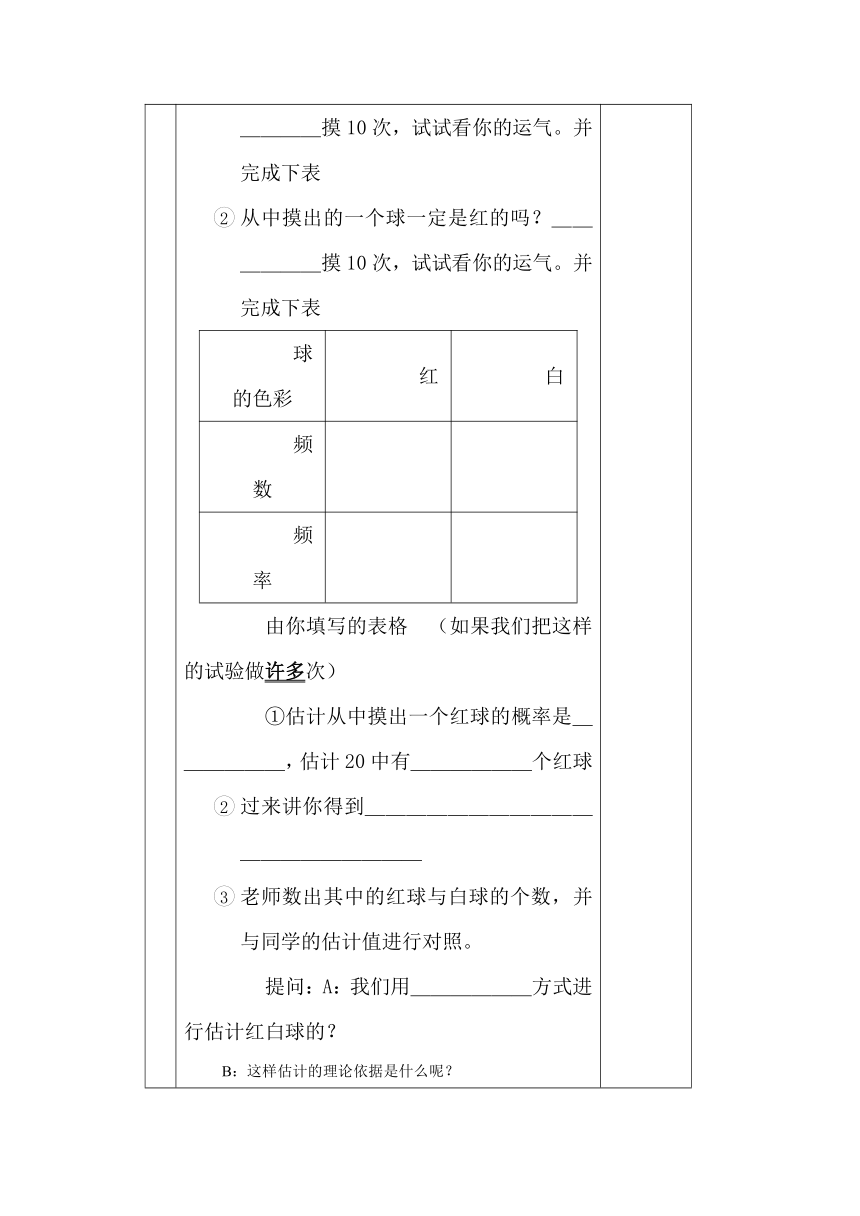
合作探究 典型例题:例1 问题二:我们用抽签的方法从3名同学中选一名去参加某音乐会。事先准备三张相同的小纸条,并在1张纸条画上记号,其余2张纸条不画。把3张纸条放在一个盒子中搅匀,然后让3名同学去摸纸条,这种方法公平吗?学生讨论:提出质疑:抽签有先有后,如果先抽的人抽到了,后抽的人就抽不到了。可是,如果先抽的人没有抽到,后抽的人抽到的机会就大了?先抽的人与后抽的人中签的概率一样吗?有老师引导学生探索: 下面我们就来算一算各人中签的概率:假设这3名同学分别记作甲、乙、丙,他们抽签的顺序依次为:甲第一,乙第二,丙第三。三张小纸条中,画有记号的纸条记作A,余下的两张没有记号的纸条分别记作和。我们用表格列出所有可能出现的结果:第一次(甲抽)第二次(乙抽)第三次(丙抽)所有可能出现的结果开始AA A A A A AA A A A 从上图可以看出,甲、乙、丙依次抽签,一共六种可能的结果,并且它们是等可能的。A和A这两种结果为甲中签,P(甲中签)=1/3A和A这两种结果为乙中签,P(乙中签)=1/3A和A这两种结果为丙中签,P(丙中签)=1/3三、提炼总结:通过上面的分析我们看到,抽签虽然有先有后,但是先抽的人和后抽的人中签的可能性是一样的,因此对每个人来说都是公平的,所以不必挣着先抽签。
当堂达标 用抽签的方法从三名同学种选两名去看电影。这种方法公平吗?请说明理由。小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽的一分,谁先得十分,谁就得胜。这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)分别转动如图所示的两个转盘各转一次。求指针一次指向红色区域,另一次指向黄色区域的概率。请利用这两个转盘,设计一个对游戏双方公平的游戏。
学习反思:
课题 9.2概率帮你做估计 自主空间
学习目标 1.通过样本的频率的性质对总体的概率进行估计。2.利用概率原理,设计方案对总体进行估计 加强学生学以至用的意识
学习重点 体会样本的频率对总体的概率的估计
学习难点 设计方案对总体进行估计
教学流程
预习导航 什么叫频数?______________________什么叫频率?______________________什么叫概率?_____________________概率的计算方法是_________频率与概率的关系是什么?_______________抽样调查时为什么要选择样本?___________________________我们对样本的性质抽查目的是什么?___________________________
合作探究 一、典型例题:实验一:集中所有的红球,白球共20个,球除色彩外全部一样外无区别,你知道袋中有多少红球与白球吗?学生进行讨论?并给出意见师生进行实验操作分小组进行 (注意摸后放回)从中摸出的一个球一定是红的吗?______摸10次,试试看你的运气。并完成下表从中摸出的一个球一定是红的吗?______摸10次,试试看你的运气。并完成下表球的色彩红白频数频率由你填写的表格 (如果我们把这样的试验做许多次)①估计从中摸出一个红球的概率是______,估计20中有______个红球过来讲你得到____________________老师数出其中的红球与白球的个数,并与同学的估计值进行对照。提问:A:我们用______方式进行估计红白球的?B:这样估计的理论依据是什么呢?二、展示交流:老师数10个白球放入袋中 并放一把红球当中,不准把球倒出来数,你估计袋中有多少个红球呢?学生自由讨论,并提出解决问题的方案:三、提炼总结:
当堂达标 1. 一个盒子中有8个黑棋和32个白棋,任意摸出一个,摸到黑棋的概率有多大?若任意摸出10个,你能推断这10个中可能有几个黑棋吗?为什么? 2.一个口袋中有8个白球和若干个黑球,如果不许将球倒出来数,那么你能估计出其中的黑球数吗 3.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记 的鱼有10条,则估计池塘里有鱼多少条?
学习反思:
课题 9.3保险公司怎样才能不亏本 自主空间
学习目标 1、使学生进一步掌握概率的概念2、会利用概率计算随机事件发生的平均次数3、体会概率在保险业中的应用4、培养学生把数学问题转化为数学模型的能力5、培养提高学生能用数学知识解决实际问题的能力.
学习重点 利用概率知识解决实际问题
学习难点 培养学生把数学问题转化为数学模型的能力
教学流程
预习导航 (1)一个篮球运动员投篮命中的概率为0.8,是不是说他每投篮10次就一定有8次命中?应该如何理解?(2)一副洗好的52张小扑克牌中(没有大小王),闭上眼睛,随机地抽出一张求下面事件的频率.(1)它是10;(2)它是黑色的.
合作探究 一、新知探究:一般地,如果随机事件A发生的概率是P(A),那么在相同的条件下重复n次试验,事件A发生的次数的平均值m为n×P(A)。二、典型例题: 例1、 如果你是保险公司的负责人,应该如何制定保险费用和赔偿金额? 某航班每次约有100名乘客。一次飞行中飞机失事的概率为p=0.00005,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿40万人民币。平均来说,保险公司应该如何收取保险费呢?分组讨论,保险公司怎样才能不亏本?三、展示交流1.人说:“抛掷两个普通的正方体骰子,掷得的两个6的频率应是的一半,也就是”,这一说法是错误对吗?2.苏州市区某居民小区共有800户家庭,有关部门准备对该小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水的情况。该部门通过随机抽样,调查了其中的30户家庭,已知这30户家庭共有87人。(1)这30户家庭平均每户__________人;(精确到人)(2)这30户家庭的月用水量见下表:月用水量()4671214151618202528户数12332534421求这30户家庭的人均日用水量;(一个月按30天计算,精确到)(3)根据上述数据,试估计该小区的日用水量?(精确到)3.一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有其他区别,其中装有白球5只,红球3只,黑球1只,袋中的球已经搅匀.闭上眼睛随机从袋中取出1只球,分别求取出的球是白球、黑球、红球的概率.4.如今,我国的福彩、体彩等形式的彩票已吸引了不少人,不少同学会感到十分神秘,其实这只是一个概率问题.针对这一问题,我们做一个有趣的游戏:小明对小亮说:“我向空中抛2枚同样的—元硬币,如果落地后一正一反,你给我10元钱,如果落地后两面一样,我给你10元线.”结果小亮欣然答应,请问,你觉得这个游戏公平吗
当堂达标 1、一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后均放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是 .2、人寿保险公司的一张关于某地区的生命表的部分摘录如下:年龄活到该年龄的人数在该年龄的死亡人数40805008925078009951606989112007045502211980160782001………根据上表解下列各题:某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?(保留三个有效数字)(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?3、为了调查今年有多少名学生参加中考,小华从全市所有家庭中随机抽查了200个家庭,发现其中有10个家庭有子女参加中考。(1)本次抽查的200个家庭中,有子女参加中考的家庭的频率是多少?(2)如果你随机调查一个家庭,估计该家庭有子女参加中考的概率是多少?(3)已知全市约有1.3×106个家庭,假设有子女参加中考的每个家庭中只有一名考生,请你估计今年全市有多少名考生参加中考?
学习反思:
先抽的人没有抽到呢?
先抽的人中签的可能性大,后抽的人吃亏
红
黄
红
黄
学习目标 1.让学生经历抽签的探索过程,感受抽签方法2.通过探索,由学生总结“先抽的人与后抽的人”中签的概率是否一样3.探索和经验总结,抽签的方法是合理的
学习重点 通过探索,得出“先抽的人与后抽的人”中签的概率一样
学习难点 探索和经验总结,抽签的方法是合理的
教学流程
预习导航 有一张电影票,小明和小丽用抽签的方法来决定谁可以去看电影,于是准备了两张相同的小纸条,一张上面是“去”,另一张上面是“不去”,谁抽到“去”,则这个人就去看电影,这种方法公平吗?
合作探究 典型例题:例1 问题二:我们用抽签的方法从3名同学中选一名去参加某音乐会。事先准备三张相同的小纸条,并在1张纸条画上记号,其余2张纸条不画。把3张纸条放在一个盒子中搅匀,然后让3名同学去摸纸条,这种方法公平吗?学生讨论:提出质疑:抽签有先有后,如果先抽的人抽到了,后抽的人就抽不到了。可是,如果先抽的人没有抽到,后抽的人抽到的机会就大了?先抽的人与后抽的人中签的概率一样吗?有老师引导学生探索: 下面我们就来算一算各人中签的概率:假设这3名同学分别记作甲、乙、丙,他们抽签的顺序依次为:甲第一,乙第二,丙第三。三张小纸条中,画有记号的纸条记作A,余下的两张没有记号的纸条分别记作和。我们用表格列出所有可能出现的结果:第一次(甲抽)第二次(乙抽)第三次(丙抽)所有可能出现的结果开始AA A A A A AA A A A 从上图可以看出,甲、乙、丙依次抽签,一共六种可能的结果,并且它们是等可能的。A和A这两种结果为甲中签,P(甲中签)=1/3A和A这两种结果为乙中签,P(乙中签)=1/3A和A这两种结果为丙中签,P(丙中签)=1/3三、提炼总结:通过上面的分析我们看到,抽签虽然有先有后,但是先抽的人和后抽的人中签的可能性是一样的,因此对每个人来说都是公平的,所以不必挣着先抽签。
当堂达标 用抽签的方法从三名同学种选两名去看电影。这种方法公平吗?请说明理由。小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽的一分,谁先得十分,谁就得胜。这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)分别转动如图所示的两个转盘各转一次。求指针一次指向红色区域,另一次指向黄色区域的概率。请利用这两个转盘,设计一个对游戏双方公平的游戏。
学习反思:
课题 9.2概率帮你做估计 自主空间
学习目标 1.通过样本的频率的性质对总体的概率进行估计。2.利用概率原理,设计方案对总体进行估计 加强学生学以至用的意识
学习重点 体会样本的频率对总体的概率的估计
学习难点 设计方案对总体进行估计
教学流程
预习导航 什么叫频数?______________________什么叫频率?______________________什么叫概率?_____________________概率的计算方法是_________频率与概率的关系是什么?_______________抽样调查时为什么要选择样本?___________________________我们对样本的性质抽查目的是什么?___________________________
合作探究 一、典型例题:实验一:集中所有的红球,白球共20个,球除色彩外全部一样外无区别,你知道袋中有多少红球与白球吗?学生进行讨论?并给出意见师生进行实验操作分小组进行 (注意摸后放回)从中摸出的一个球一定是红的吗?______摸10次,试试看你的运气。并完成下表从中摸出的一个球一定是红的吗?______摸10次,试试看你的运气。并完成下表球的色彩红白频数频率由你填写的表格 (如果我们把这样的试验做许多次)①估计从中摸出一个红球的概率是______,估计20中有______个红球过来讲你得到____________________老师数出其中的红球与白球的个数,并与同学的估计值进行对照。提问:A:我们用______方式进行估计红白球的?B:这样估计的理论依据是什么呢?二、展示交流:老师数10个白球放入袋中 并放一把红球当中,不准把球倒出来数,你估计袋中有多少个红球呢?学生自由讨论,并提出解决问题的方案:三、提炼总结:
当堂达标 1. 一个盒子中有8个黑棋和32个白棋,任意摸出一个,摸到黑棋的概率有多大?若任意摸出10个,你能推断这10个中可能有几个黑棋吗?为什么? 2.一个口袋中有8个白球和若干个黑球,如果不许将球倒出来数,那么你能估计出其中的黑球数吗 3.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记 的鱼有10条,则估计池塘里有鱼多少条?
学习反思:
课题 9.3保险公司怎样才能不亏本 自主空间
学习目标 1、使学生进一步掌握概率的概念2、会利用概率计算随机事件发生的平均次数3、体会概率在保险业中的应用4、培养学生把数学问题转化为数学模型的能力5、培养提高学生能用数学知识解决实际问题的能力.
学习重点 利用概率知识解决实际问题
学习难点 培养学生把数学问题转化为数学模型的能力
教学流程
预习导航 (1)一个篮球运动员投篮命中的概率为0.8,是不是说他每投篮10次就一定有8次命中?应该如何理解?(2)一副洗好的52张小扑克牌中(没有大小王),闭上眼睛,随机地抽出一张求下面事件的频率.(1)它是10;(2)它是黑色的.
合作探究 一、新知探究:一般地,如果随机事件A发生的概率是P(A),那么在相同的条件下重复n次试验,事件A发生的次数的平均值m为n×P(A)。二、典型例题: 例1、 如果你是保险公司的负责人,应该如何制定保险费用和赔偿金额? 某航班每次约有100名乘客。一次飞行中飞机失事的概率为p=0.00005,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿40万人民币。平均来说,保险公司应该如何收取保险费呢?分组讨论,保险公司怎样才能不亏本?三、展示交流1.人说:“抛掷两个普通的正方体骰子,掷得的两个6的频率应是的一半,也就是”,这一说法是错误对吗?2.苏州市区某居民小区共有800户家庭,有关部门准备对该小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水的情况。该部门通过随机抽样,调查了其中的30户家庭,已知这30户家庭共有87人。(1)这30户家庭平均每户__________人;(精确到人)(2)这30户家庭的月用水量见下表:月用水量()4671214151618202528户数12332534421求这30户家庭的人均日用水量;(一个月按30天计算,精确到)(3)根据上述数据,试估计该小区的日用水量?(精确到)3.一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有其他区别,其中装有白球5只,红球3只,黑球1只,袋中的球已经搅匀.闭上眼睛随机从袋中取出1只球,分别求取出的球是白球、黑球、红球的概率.4.如今,我国的福彩、体彩等形式的彩票已吸引了不少人,不少同学会感到十分神秘,其实这只是一个概率问题.针对这一问题,我们做一个有趣的游戏:小明对小亮说:“我向空中抛2枚同样的—元硬币,如果落地后一正一反,你给我10元钱,如果落地后两面一样,我给你10元线.”结果小亮欣然答应,请问,你觉得这个游戏公平吗
当堂达标 1、一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后均放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是 .2、人寿保险公司的一张关于某地区的生命表的部分摘录如下:年龄活到该年龄的人数在该年龄的死亡人数40805008925078009951606989112007045502211980160782001………根据上表解下列各题:某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?(保留三个有效数字)(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?3、为了调查今年有多少名学生参加中考,小华从全市所有家庭中随机抽查了200个家庭,发现其中有10个家庭有子女参加中考。(1)本次抽查的200个家庭中,有子女参加中考的家庭的频率是多少?(2)如果你随机调查一个家庭,估计该家庭有子女参加中考的概率是多少?(3)已知全市约有1.3×106个家庭,假设有子女参加中考的每个家庭中只有一名考生,请你估计今年全市有多少名考生参加中考?
学习反思:
先抽的人没有抽到呢?
先抽的人中签的可能性大,后抽的人吃亏
红
黄
红
黄
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
