第二十章 数据的分析单元测试卷(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十章 数据的分析单元测试卷
(满分:100分 时间:90分钟)
班级_________ 姓名_________ 学号_________ 分数_________
一、单选题(共10小题,每小题3分,共计30分)
1.(2020·靖安市九年级期中)某排球队名场上队员的身高(单位:)是:,,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
2.(2020·山东菏泽市·八年级期末)小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
A.众数是6吨 B.平均数是5吨 C.中位数是5吨 D.方差是
3.(2020·吉林长春市八年级期末)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
甲 乙 丙 丁
平均数(环) 9.14 9.15 9.14 9.15
方差 6.6 6.8 6.7 6.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
4.(2020·天津东丽区·八年级期末)有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )
A.方差 B.中位数 C.众数 D.平均数
5.(2020·江苏省九年级期中)某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
6.(2020·河北邯郸市·八年级期末)某校九年级“诗歌大会”比赛中,各班代表队得分如下(单位:分):9,7,8,7,9,7,6,则各代表队得分的中位数是( ???)
A.9分 B.8分 C.7分 D.6分
7.(2020·集贤县期末)小明同学5次数学小测验成绩分别是90分、95分、85分、95分、100分,则小明这5次成绩的众数和中位数分别是( )
A.95分、95分 B.85分、95分 C.95分、85分 D.95分、90分
8.(2020·江西吉安市·八年级期末)某青年排球队12名队员年龄情况如下:
年龄 18 19 20 21 22
人数 1 4 3 2 2
则这12名队员年龄的众数、中位数分别是( )
A.20,19 B.19,19 C.19,20.5 D.19,20
9.(2020·塔城地区期末)关于2、6、1、10、6的这组数据,下列说法正确的是( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
10.(2020·湖州市八年级期中)若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则的值为( ).
A.1 B.6
C.1或6 D.5或6
二、填空题(共5小题,每小题4分,共计20分)
11.(2020·内蒙古包头市·八年级期末)某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图如图,可计算出该店当月销售出水果的平均价格是______元
12.(2020·甘肃庆阳市·八年级期末)甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
13.(2020·靖安市九年级期中)甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是______(填“甲”或“乙”)
14.(2020·安徽合肥市·八年级期末)李明同学进行射击练习,两发子弹各打中5环,四发子弹各打中8环,三发子弹各打中9环.一发子弹打中10环,则他射击的平均成绩是________环.
15.(2020·云南昆明三中八年级期末)未测试两种电子表的走时误差,做了如下统计
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是 .
三、解答题(共5小题,每小题10分,共计50分)
16.(2020·四川八年级期末)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 0 1 2 3 4 5
人数 11 15 23 28 18 5
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
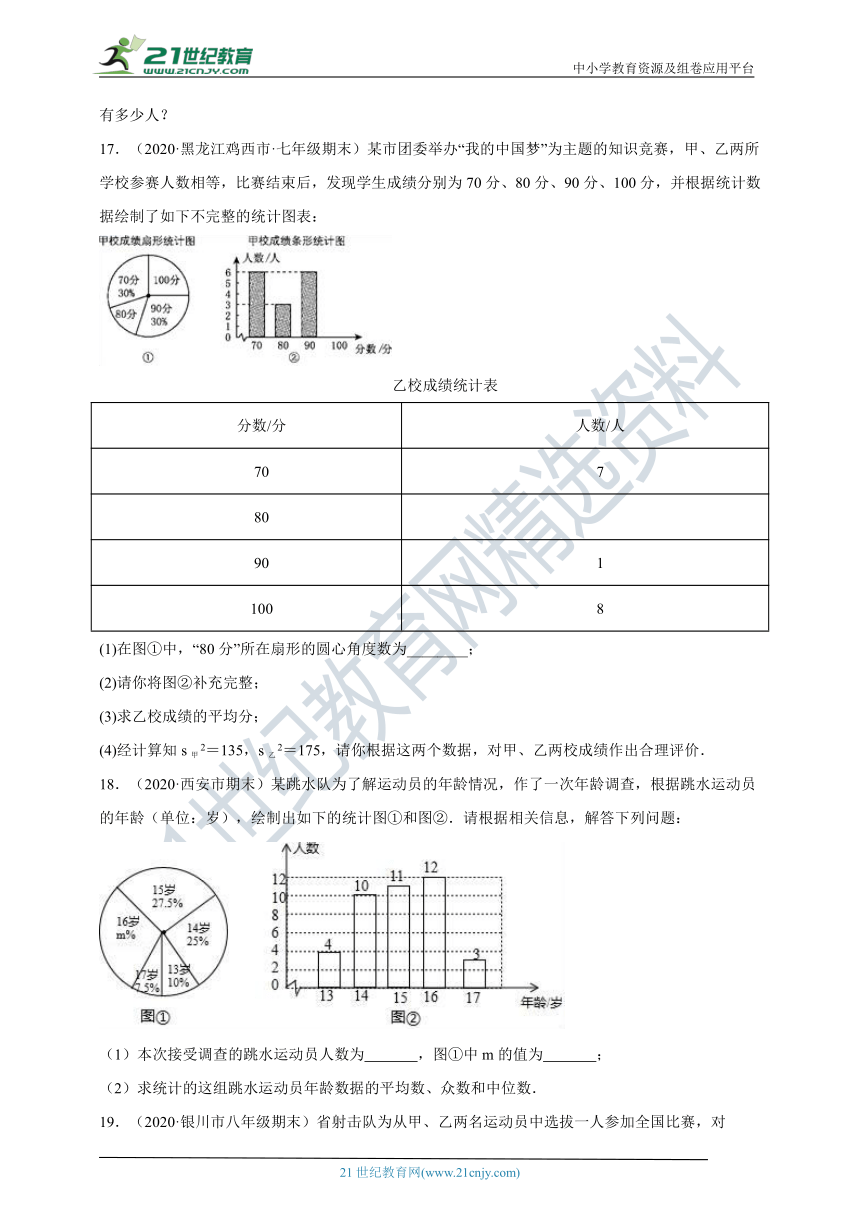
17.(2020·黑龙江鸡西市·七年级期末)某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数/分 人数/人
70 7
80
90 1
100 8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
18.(2020·西安市期末)某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的跳水运动员人数为 ,图①中m的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
19.(2020·银川市八年级期末)省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=[])
20.(2020·河北沧州市·八年级期末)某同学上学期的数学历次测验成绩如下表所示:
测验类别 平时测验 期中测验 期末测验
第1次 第2次 第3次
成绩 100 106 106 105 110
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数).
答案
一、单选题(共10小题,每小题3分,共计30分)
1.A 2.C 3.D 4.A 5.C 6.C 7.A 8.D 9.A.10.C
二、填空题(共5小题,每小题4分,共计20分)
11.
12.>
13.甲
14.7.9
15.甲
三、解答题(共5小题,每小题10分,共计50分)
16.【详解】(1)∵总人数为11+15+23+28+18+5=100,
∴中位数为第50、51个数据的平均数,即中位数为=3次,众数为3次,
其中中位数表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次),
故答案为3、3、表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次);
(2)≈2(次),
答:这天部分出行学生平均每人使用共享单车约2次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
17.试题解析:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
18.【详解】
解:(1)4÷10%=40(人),
m=100-27.5-25-7.5-10=30;
故答案为40,30.
(2)观察条形统计图,
∵,
∴这组数据的平均数为15;
∵在这组数据中,16出现了12次,出现的次数最多,
∴这组数据的众数为16;
∵将这组数据按照从小到大的顺序排列,其中处于中间的两个数都是15,有,
∴这组数据的中位数为15.
19.【详解】
解:(1)9;9.
(2)s2甲=
==;
s2乙=
==.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
20.详解:(1)数据排列为:100,105,106,106,110;
所以中位数为106,众数为106.
(2)平时数学平均成绩为:=104.
(3)104×0.3+105×0.3+110×0.4=107分.
_21?????????è?????(www.21cnjy.com)_
第二十章 数据的分析单元测试卷
(满分:100分 时间:90分钟)
班级_________ 姓名_________ 学号_________ 分数_________
一、单选题(共10小题,每小题3分,共计30分)
1.(2020·靖安市九年级期中)某排球队名场上队员的身高(单位:)是:,,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
2.(2020·山东菏泽市·八年级期末)小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
A.众数是6吨 B.平均数是5吨 C.中位数是5吨 D.方差是
3.(2020·吉林长春市八年级期末)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
甲 乙 丙 丁
平均数(环) 9.14 9.15 9.14 9.15
方差 6.6 6.8 6.7 6.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
4.(2020·天津东丽区·八年级期末)有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )
A.方差 B.中位数 C.众数 D.平均数
5.(2020·江苏省九年级期中)某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
6.(2020·河北邯郸市·八年级期末)某校九年级“诗歌大会”比赛中,各班代表队得分如下(单位:分):9,7,8,7,9,7,6,则各代表队得分的中位数是( ???)
A.9分 B.8分 C.7分 D.6分
7.(2020·集贤县期末)小明同学5次数学小测验成绩分别是90分、95分、85分、95分、100分,则小明这5次成绩的众数和中位数分别是( )
A.95分、95分 B.85分、95分 C.95分、85分 D.95分、90分
8.(2020·江西吉安市·八年级期末)某青年排球队12名队员年龄情况如下:
年龄 18 19 20 21 22
人数 1 4 3 2 2
则这12名队员年龄的众数、中位数分别是( )
A.20,19 B.19,19 C.19,20.5 D.19,20
9.(2020·塔城地区期末)关于2、6、1、10、6的这组数据,下列说法正确的是( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
10.(2020·湖州市八年级期中)若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则的值为( ).
A.1 B.6
C.1或6 D.5或6
二、填空题(共5小题,每小题4分,共计20分)
11.(2020·内蒙古包头市·八年级期末)某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图如图,可计算出该店当月销售出水果的平均价格是______元
12.(2020·甘肃庆阳市·八年级期末)甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
13.(2020·靖安市九年级期中)甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是______(填“甲”或“乙”)
14.(2020·安徽合肥市·八年级期末)李明同学进行射击练习,两发子弹各打中5环,四发子弹各打中8环,三发子弹各打中9环.一发子弹打中10环,则他射击的平均成绩是________环.
15.(2020·云南昆明三中八年级期末)未测试两种电子表的走时误差,做了如下统计
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是 .
三、解答题(共5小题,每小题10分,共计50分)
16.(2020·四川八年级期末)近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 0 1 2 3 4 5
人数 11 15 23 28 18 5
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
17.(2020·黑龙江鸡西市·七年级期末)某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数/分 人数/人
70 7
80
90 1
100 8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
18.(2020·西安市期末)某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的跳水运动员人数为 ,图①中m的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
19.(2020·银川市八年级期末)省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=[])
20.(2020·河北沧州市·八年级期末)某同学上学期的数学历次测验成绩如下表所示:
测验类别 平时测验 期中测验 期末测验
第1次 第2次 第3次
成绩 100 106 106 105 110
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数).
答案
一、单选题(共10小题,每小题3分,共计30分)
1.A 2.C 3.D 4.A 5.C 6.C 7.A 8.D 9.A.10.C
二、填空题(共5小题,每小题4分,共计20分)
11.
12.>
13.甲
14.7.9
15.甲
三、解答题(共5小题,每小题10分,共计50分)
16.【详解】(1)∵总人数为11+15+23+28+18+5=100,
∴中位数为第50、51个数据的平均数,即中位数为=3次,众数为3次,
其中中位数表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次),
故答案为3、3、表示这部分出行学生这天约有一半使用共享单车的次数在3次以上(或3次);
(2)≈2(次),
答:这天部分出行学生平均每人使用共享单车约2次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
17.试题解析:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
18.【详解】
解:(1)4÷10%=40(人),
m=100-27.5-25-7.5-10=30;
故答案为40,30.
(2)观察条形统计图,
∵,
∴这组数据的平均数为15;
∵在这组数据中,16出现了12次,出现的次数最多,
∴这组数据的众数为16;
∵将这组数据按照从小到大的顺序排列,其中处于中间的两个数都是15,有,
∴这组数据的中位数为15.
19.【详解】
解:(1)9;9.
(2)s2甲=
==;
s2乙=
==.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
20.详解:(1)数据排列为:100,105,106,106,110;
所以中位数为106,众数为106.
(2)平时数学平均成绩为:=104.
(3)104×0.3+105×0.3+110×0.4=107分.
_21?????????è?????(www.21cnjy.com)_
