20.2 数据的波动程度同步练习(含答案)
文档属性
| 名称 | 20.2 数据的波动程度同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.2 数据的波动程度同步练习
一、单选题(共10小题)
1.(2020·浙江九年级期末)一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是
A.平均数 B.中位数 C.众数 D.方差
2.(2020·厦门市八年级期末)为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为:==13,==15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A.甲 B.乙 C.丙 D.丁
3.(2020·安庆市八年级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
4.(2020·山东泰安市·九年级期末)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲,乙两组数据,如下表:
甲 2 6 7 7 8
乙 2 3 4 8 8
关于以上数据,说法正确的是( )
A.甲、乙的众数相同 B.甲、乙的中位数相同
C.甲的平均数小于乙的平均数 D.甲的方差小于乙的方差
5.(2020·南通市八年级期中)甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,方差分别是,,,.在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
6.(2020·长沙市八年级期末)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示:
甲 乙 丙 丁
24 24 23 20
2.1 1.9 2 1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( ??)
A.甲 B.乙 C.丙 D.丁
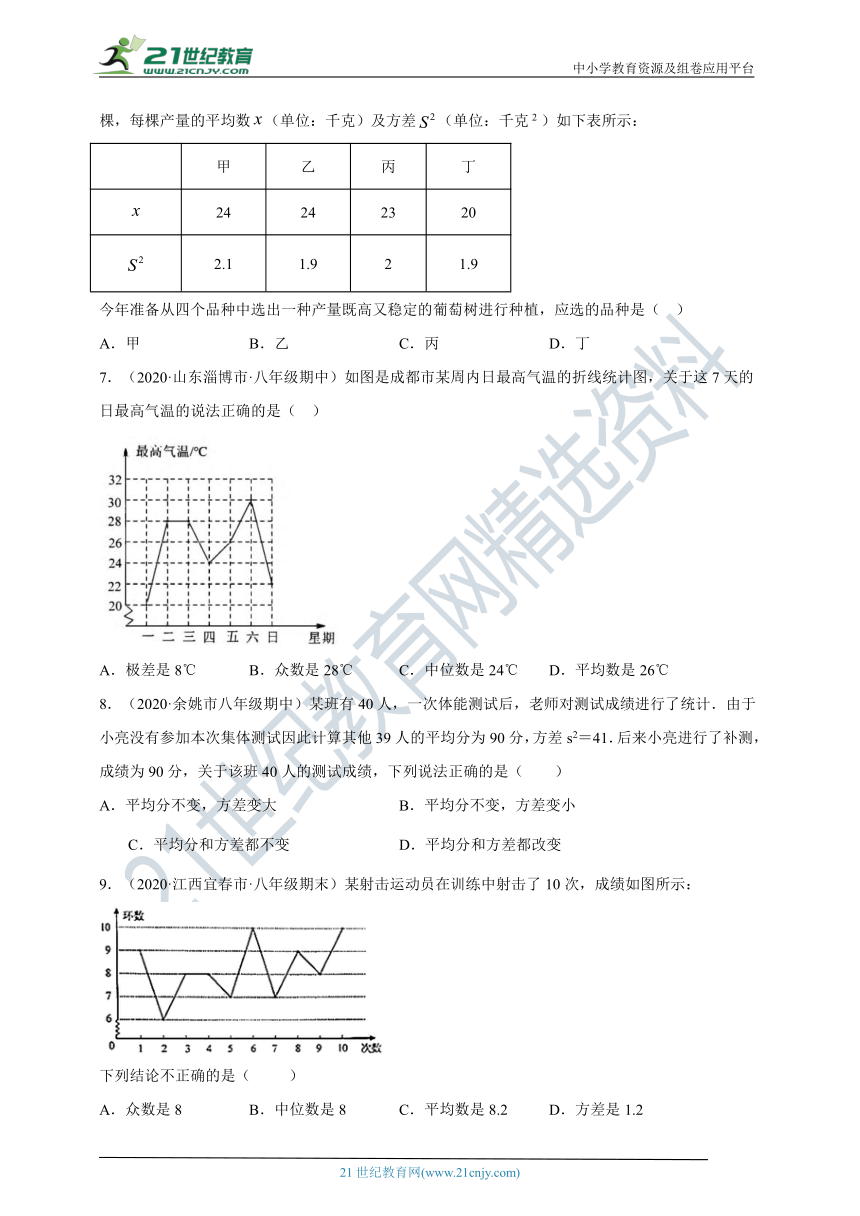
7.(2020·山东淄博市·八年级期中)如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A.极差是8℃ B.众数是28℃ C.中位数是24℃ D.平均数是26℃
8.(2020·余姚市八年级期中)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
9.(2020·江西宜春市·八年级期末)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8 C.平均数是8.2 D.方差是1.2
10.(2020·巴彦淖尔市临河区期末)一组数据3、2、1、2、2的众数,中位数,方差分别是( )
A.2,1,0.4 B.2,2,0.4
C.3,1,2 D.2,1,0.2
二、填空题(共5小题)
11.(2020·江西宜春市·八年级期末)若一组数据的平均数为6,众数为5,则这组数据的方差为__________.
12.(2020·广西南宁市期末)甲,乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为:9,8,9,6,10,6.甲,乙两人平均成绩相等,乙成绩的方差为4,那么成绩较为稳定的是______.(填“甲”或“乙”)
13.(2020·吉林延边朝鲜族自治州·八年级期末)有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是_______.
14.(2020·海淀区八年级期中)某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_____.
甲 乙 丙 丁
7 8 8 7
s2 1 1.2 0.9 1.8
15.(2020·福建龙岩市·九年级期中)若一组数据1,2,x,4的众数是1,则这组数据的方差为_____.
三、解答题(共2小题)
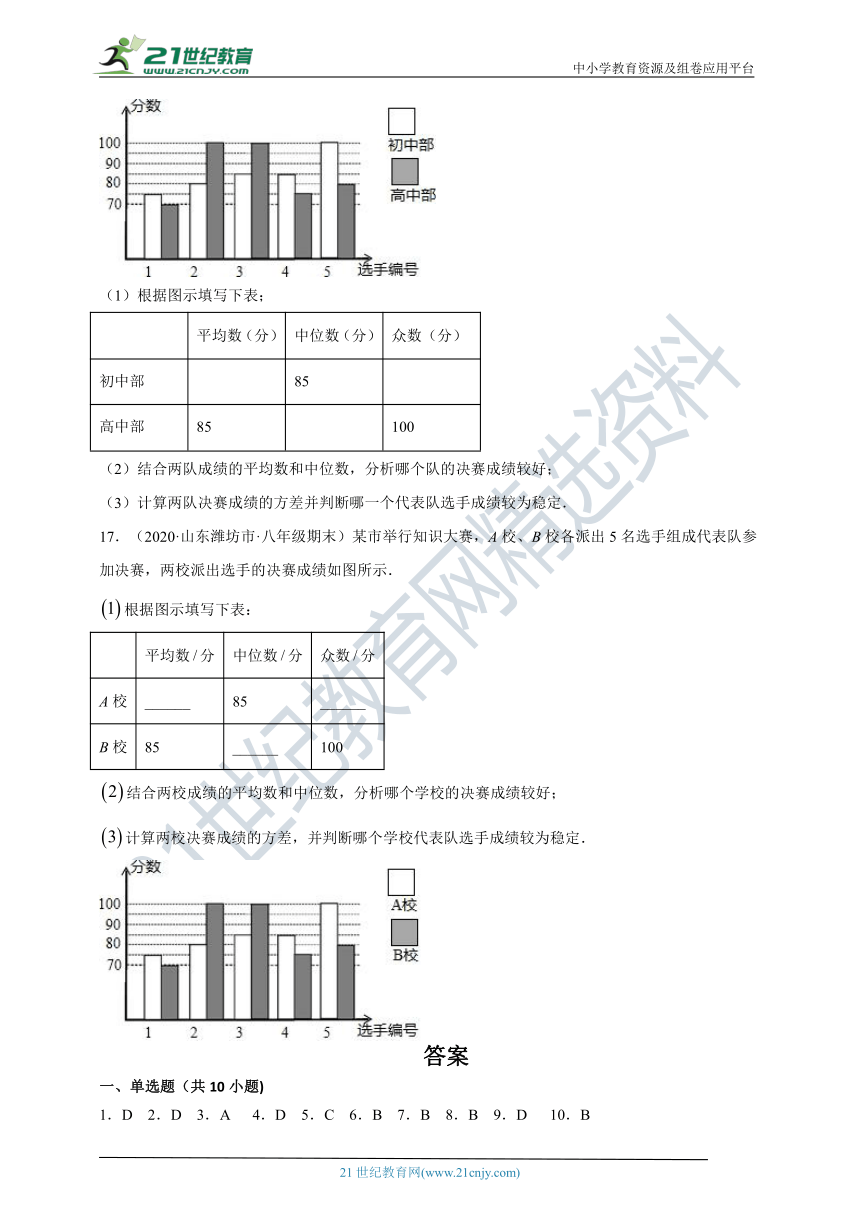
16.(2020·南昌市期末)我市某中学举行“中国梦?校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
平均数(分) 中位数(分) 众数(分)
初中部
85
高中部 85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
17.(2020·山东潍坊市·八年级期末)某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
根据图示填写下表:
平均数分 中位数分 众数分
A校 ______ 85 ______
B校 85 ______ 100
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
答案
一、单选题(共10小题)
1.D 2.D 3.A 4.D 5.C 6.B 7.B 8.B 9.D 10.B
二、填空题(共5小题)
11.
12.甲.
13.小林
14.丙
15.1.5
三、解答题(共2小题)
16.(解:(1)填表如下:
平均数(分) 中位数(分) 众数(分)
初中部 85 85 85
高中部 85 80 100
(2)初中部成绩好些.
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些.
(3)∵,
,
∴<,因此,初中代表队选手成绩较为稳定.
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答.
(2)根据平均数和中位数的统计意义分析得出即可.
(3)分别求出初中、高中部的方差比较即可.
17.【详解】
解:;85;80.
A校平均数= 分
A校的成绩:75.80.85.85.100,众数为85分
B校的成绩:70.75.80.100.100,中位数为80分
校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些.
校的方差,
B校的方差.
,
因此,A校代表队选手成绩较为稳定.
_21?????????è?????(www.21cnjy.com)_
20.2 数据的波动程度同步练习
一、单选题(共10小题)
1.(2020·浙江九年级期末)一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是
A.平均数 B.中位数 C.众数 D.方差
2.(2020·厦门市八年级期末)为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为:==13,==15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A.甲 B.乙 C.丙 D.丁
3.(2020·安庆市八年级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
4.(2020·山东泰安市·九年级期末)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲,乙两组数据,如下表:
甲 2 6 7 7 8
乙 2 3 4 8 8
关于以上数据,说法正确的是( )
A.甲、乙的众数相同 B.甲、乙的中位数相同
C.甲的平均数小于乙的平均数 D.甲的方差小于乙的方差
5.(2020·南通市八年级期中)甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,方差分别是,,,.在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
6.(2020·长沙市八年级期末)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示:
甲 乙 丙 丁
24 24 23 20
2.1 1.9 2 1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( ??)
A.甲 B.乙 C.丙 D.丁
7.(2020·山东淄博市·八年级期中)如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A.极差是8℃ B.众数是28℃ C.中位数是24℃ D.平均数是26℃
8.(2020·余姚市八年级期中)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
9.(2020·江西宜春市·八年级期末)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8 C.平均数是8.2 D.方差是1.2
10.(2020·巴彦淖尔市临河区期末)一组数据3、2、1、2、2的众数,中位数,方差分别是( )
A.2,1,0.4 B.2,2,0.4
C.3,1,2 D.2,1,0.2
二、填空题(共5小题)
11.(2020·江西宜春市·八年级期末)若一组数据的平均数为6,众数为5,则这组数据的方差为__________.
12.(2020·广西南宁市期末)甲,乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为:9,8,9,6,10,6.甲,乙两人平均成绩相等,乙成绩的方差为4,那么成绩较为稳定的是______.(填“甲”或“乙”)
13.(2020·吉林延边朝鲜族自治州·八年级期末)有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是_______.
14.(2020·海淀区八年级期中)某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_____.
甲 乙 丙 丁
7 8 8 7
s2 1 1.2 0.9 1.8
15.(2020·福建龙岩市·九年级期中)若一组数据1,2,x,4的众数是1,则这组数据的方差为_____.
三、解答题(共2小题)
16.(2020·南昌市期末)我市某中学举行“中国梦?校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
平均数(分) 中位数(分) 众数(分)
初中部
85
高中部 85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
17.(2020·山东潍坊市·八年级期末)某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
根据图示填写下表:
平均数分 中位数分 众数分
A校 ______ 85 ______
B校 85 ______ 100
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
答案
一、单选题(共10小题)
1.D 2.D 3.A 4.D 5.C 6.B 7.B 8.B 9.D 10.B
二、填空题(共5小题)
11.
12.甲.
13.小林
14.丙
15.1.5
三、解答题(共2小题)
16.(解:(1)填表如下:
平均数(分) 中位数(分) 众数(分)
初中部 85 85 85
高中部 85 80 100
(2)初中部成绩好些.
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些.
(3)∵,
,
∴<,因此,初中代表队选手成绩较为稳定.
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答.
(2)根据平均数和中位数的统计意义分析得出即可.
(3)分别求出初中、高中部的方差比较即可.
17.【详解】
解:;85;80.
A校平均数= 分
A校的成绩:75.80.85.85.100,众数为85分
B校的成绩:70.75.80.100.100,中位数为80分
校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些.
校的方差,
B校的方差.
,
因此,A校代表队选手成绩较为稳定.
_21?????????è?????(www.21cnjy.com)_
