2020-2021学年北师大版七年级下册3.2用关系式表示的变量之间关系课时训练试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年北师大版七年级下册3.2用关系式表示的变量之间关系课时训练试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 78.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 09:04:12 | ||
图片预览



文档简介
北师大版七下3.2用关系式表示的变量之间关系课时训练(含答案解析)
一、选择题
某汽车油箱中盛有油100L,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是
A.
B.
C.
D.
变量x与y之间的关系是,当时,自变量x的值是
A.
13
B.
5
C.
2
D.
从A地向B地打长途电话,通话3分钟以内收费元,3分钟后通话时间每增加1分钟加收1元.若通话时间为单位:分,,且x为整数,则通话费用单位:元与通话时间单位:分的关系式是?
?
A.
B.
C.
D.
某油箱容量为60L的汽车,加满汽油行驶了100km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为xkm,油箱中剩油量为yL,则y与x之间的关系式和自变量的取值范围分别是?
?
A.
B.
C.
D.
如图所示,在长方形ABCD中,,,P是CD上的动点,且不与点C,D重合,设,梯形ABCP的面积为y,则y与x之间的关系式和自变量的取值范围分别是
A.
;
B.
;
C.
;
D.
;
我国是水资源比较贫乏的国家,所以各省市都采取了各项措施加强公民的节水意识某市规定了如下的用水收费标准:每户每月的用水不超过10立方米时,水费按每立方米元收费,超过10立方米时,不超过的部分仍按每立方米元收费,超出部分按每立方米3元收费设该市某户7月份用水量为立方米,应交水费为元用水不超过10立方米时与超过10立方米时,y与x之间的关系式是?
?
A.
当时,当时,
B.
当时,当时,
C.
当时,当时,
D.
当时,当时,
如图所示,在中,已知,高线,动点由点C沿CB向点B移动不与点B重合设的长为x,的面积为S,则S关于x的关系式为?
?
?
B.
C.
D.
变量x与y之间的关系是,当自变量时,因变量y的值是
A.
B.
C.
1
D.
2
如图所示是小思所设计的函数值计算程序.若输入x的值为2,则输出的y值为?
?
A.
5
B.
9
C.
D.
0
如图,三角形有规律地从里到外逐层排列.设y为第n层为正整数三角形的个数,则下列关系式中正确的是?
?
A.
B.
C.
D.
二、填空题
在登山过程中,海拔每升高1千米,气温下降,已知某登山大本营所在的位置的气温是,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是,那么y关于x的关系式是??????.
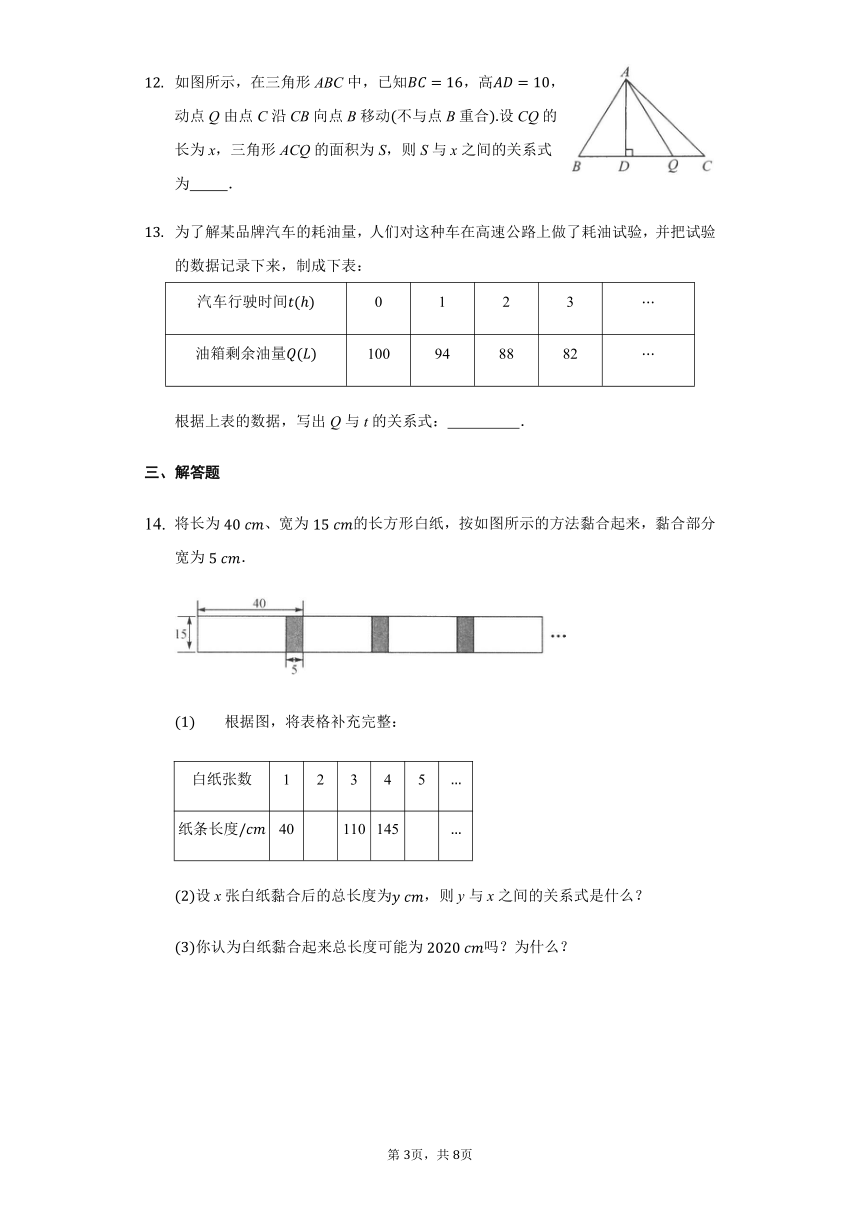
如图所示,在三角形ABC中,已知,高,动点Q由点C沿CB向点B移动不与点B重合设CQ的长为x,三角形ACQ的面积为S,则S与x之间的关系式为??????????.
为了解某品牌汽车的耗油量,人们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间
0
1
2
3
油箱剩余油量
100
94
88
82
根据上表的数据,写出Q与t的关系式:?????????????
?
?.
三、解答题
将长为、宽为的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为.
根据图,将表格补充完整:
白纸张数
1
2
3
4
5
纸条长度
40
110
145
设x张白纸黏合后的总长度为,则y与x之间的关系式是什么?
你认为白纸黏合起来总长度可能为吗?为什么?
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为,则变量N与n之间的关系可以表示为.
在这个关系式中,自变量、因变量各是什么?
在这个关系式中,n能取什么样的值?
利用这个关系式计算六边形的内角和;
当边数每增加1时,多边形的内角和如何变化?
答案和解析
1.【答案】C
【解析】分析
根据油箱剩油量等于总油量减去消耗的油量列出关系式即可.
本题考查了用关系式表示变量间的关系,比较简单.
详解
解:由题意得,油箱剩油量.
故选C.
2.【答案】C
【解析】
【分析】
此题主要考查变量x与y之间的关系式,关键是掌握已知的关系式,给出因变量的值时,解方程求出相应的自变量的值即可.
直接把代入,解方程即可.
【解答】
解:当时,,
解得:.
故选C.
3.【答案】A
【解析】
【分析】
本题考查了用关系式表示变量间的关系,仔细审题得出变量与变量的关系是解题关键.
根据通话总费用超过3分钟后的超出费用,即可列出y与x的关系式.
【解答】
解:因为通话时间不超过3分钟收费均为元,超过3分钟后,每分钟收取1元,且x为整数,
故可得通话费用单位:元与通话时间单位:分的关系式:.
故选A.
4.【答案】D
【解析】
【分析】
此题主要考查了用关系式表示变量间的关系,求出每千米汽车的耗油量是解题关键.
首先求出汽车每千米耗油量,进而得出y与x之间的关系式.
【解答】
解:由题意得,每千米汽车的耗油量为:,
则油箱中剩余油量.
由已知得汽车的行驶路程最远为:,
故自变量的取值范围为.
所以.
故选D.
5.【答案】A
【解析】分析
本题考查了用关系式表示变量间的关系、自变量取值范围及梯形面积先确定梯形ABCP的上底、下底和高,代入数据即可得梯形ABCP的面积y与DP长x之间的关系式.
详解
解:由梯形面积公式知,,,,
,
即,
且不与点C,D重合
,
.
故选A.
6.【答案】D
【解析】解:当时,
当时,.
故选D.
7.【答案】A
【解析】分析
此题考查了用关系式表示变量间的关系,关键是利用三角形面积公式列出关系式.
设的长为x,得出的长为,再根据三角形的面积公式列出关系式即可.
详解
解:设的长为x,可得的长为,
所以S与x之间的关系式为.
故选A.
8.【答案】B
【解析】解:当时,,
故选:B.
把自变量x的值代入函数解析式进行计算即可得解.
本题考查了函数值的求解,是基础题,准确计算是解题的关键.
9.【答案】D
【解析】
【分析】
本题考查了用关系式表示的变量间关系,找出对应的关系式是解题的关键.
因为自变量的值为2,所以对应的关系式为,将代入该关系式即可得到结果.
【解答】
解:,所以对应的关系式为,
,即输出的y值为0.
故选D.
10.【答案】B
【解析】分析
主要考查了根据图形列出关系式据图示可知,第一层是4个,第二层是8个,第三层是12个,,第n层是4n个,即可确定y与n的关系.
详解
解:由图可知:
时,三角形有4个,即;
时,三角形有8个,即;
时,三角形有12个,即;
以此类推,
第n层为正整数三角形的个数:.
故选B.
11.【答案】
【解析】略
12.【答案】
【解析】
【分析】
本题考查了函数关系式,利用三角形的面积是解题关键.根据三角形的面积公式,可得答案.
【解答】
解:,,
,
故答案为.
13.【答案】
【解析】解:由表格可知,开始油箱中的油为,每行驶1小时,油量减少,
与t的关系式为,
故答案为.
14.【答案】解:?
180?
.
不可能.
理由:令,
解得.
因为x为整数,
所以总长度不可能为.
【解析】略
15.【答案】解:是自变量,N是因变量.
取大于2的整数.
当时,,故六边形的内角和为.
当边数每增加1时,多边形的内角和增加.
【解析】略
第2页,共2页
第1页,共1页
一、选择题
某汽车油箱中盛有油100L,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是
A.
B.
C.
D.
变量x与y之间的关系是,当时,自变量x的值是
A.
13
B.
5
C.
2
D.
从A地向B地打长途电话,通话3分钟以内收费元,3分钟后通话时间每增加1分钟加收1元.若通话时间为单位:分,,且x为整数,则通话费用单位:元与通话时间单位:分的关系式是?
?
A.
B.
C.
D.
某油箱容量为60L的汽车,加满汽油行驶了100km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为xkm,油箱中剩油量为yL,则y与x之间的关系式和自变量的取值范围分别是?
?
A.
B.
C.
D.
如图所示,在长方形ABCD中,,,P是CD上的动点,且不与点C,D重合,设,梯形ABCP的面积为y,则y与x之间的关系式和自变量的取值范围分别是
A.
;
B.
;
C.
;
D.
;
我国是水资源比较贫乏的国家,所以各省市都采取了各项措施加强公民的节水意识某市规定了如下的用水收费标准:每户每月的用水不超过10立方米时,水费按每立方米元收费,超过10立方米时,不超过的部分仍按每立方米元收费,超出部分按每立方米3元收费设该市某户7月份用水量为立方米,应交水费为元用水不超过10立方米时与超过10立方米时,y与x之间的关系式是?
?
A.
当时,当时,
B.
当时,当时,
C.
当时,当时,
D.
当时,当时,
如图所示,在中,已知,高线,动点由点C沿CB向点B移动不与点B重合设的长为x,的面积为S,则S关于x的关系式为?
?
?
B.
C.
D.
变量x与y之间的关系是,当自变量时,因变量y的值是
A.
B.
C.
1
D.
2
如图所示是小思所设计的函数值计算程序.若输入x的值为2,则输出的y值为?
?
A.
5
B.
9
C.
D.
0
如图,三角形有规律地从里到外逐层排列.设y为第n层为正整数三角形的个数,则下列关系式中正确的是?
?
A.
B.
C.
D.
二、填空题
在登山过程中,海拔每升高1千米,气温下降,已知某登山大本营所在的位置的气温是,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是,那么y关于x的关系式是??????.
如图所示,在三角形ABC中,已知,高,动点Q由点C沿CB向点B移动不与点B重合设CQ的长为x,三角形ACQ的面积为S,则S与x之间的关系式为??????????.
为了解某品牌汽车的耗油量,人们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间
0
1
2
3
油箱剩余油量
100
94
88
82
根据上表的数据,写出Q与t的关系式:?????????????
?
?.
三、解答题
将长为、宽为的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为.
根据图,将表格补充完整:
白纸张数
1
2
3
4
5
纸条长度
40
110
145
设x张白纸黏合后的总长度为,则y与x之间的关系式是什么?
你认为白纸黏合起来总长度可能为吗?为什么?
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为,则变量N与n之间的关系可以表示为.
在这个关系式中,自变量、因变量各是什么?
在这个关系式中,n能取什么样的值?
利用这个关系式计算六边形的内角和;
当边数每增加1时,多边形的内角和如何变化?
答案和解析
1.【答案】C
【解析】分析
根据油箱剩油量等于总油量减去消耗的油量列出关系式即可.
本题考查了用关系式表示变量间的关系,比较简单.
详解
解:由题意得,油箱剩油量.
故选C.
2.【答案】C
【解析】
【分析】
此题主要考查变量x与y之间的关系式,关键是掌握已知的关系式,给出因变量的值时,解方程求出相应的自变量的值即可.
直接把代入,解方程即可.
【解答】
解:当时,,
解得:.
故选C.
3.【答案】A
【解析】
【分析】
本题考查了用关系式表示变量间的关系,仔细审题得出变量与变量的关系是解题关键.
根据通话总费用超过3分钟后的超出费用,即可列出y与x的关系式.
【解答】
解:因为通话时间不超过3分钟收费均为元,超过3分钟后,每分钟收取1元,且x为整数,
故可得通话费用单位:元与通话时间单位:分的关系式:.
故选A.
4.【答案】D
【解析】
【分析】
此题主要考查了用关系式表示变量间的关系,求出每千米汽车的耗油量是解题关键.
首先求出汽车每千米耗油量,进而得出y与x之间的关系式.
【解答】
解:由题意得,每千米汽车的耗油量为:,
则油箱中剩余油量.
由已知得汽车的行驶路程最远为:,
故自变量的取值范围为.
所以.
故选D.
5.【答案】A
【解析】分析
本题考查了用关系式表示变量间的关系、自变量取值范围及梯形面积先确定梯形ABCP的上底、下底和高,代入数据即可得梯形ABCP的面积y与DP长x之间的关系式.
详解
解:由梯形面积公式知,,,,
,
即,
且不与点C,D重合
,
.
故选A.
6.【答案】D
【解析】解:当时,
当时,.
故选D.
7.【答案】A
【解析】分析
此题考查了用关系式表示变量间的关系,关键是利用三角形面积公式列出关系式.
设的长为x,得出的长为,再根据三角形的面积公式列出关系式即可.
详解
解:设的长为x,可得的长为,
所以S与x之间的关系式为.
故选A.
8.【答案】B
【解析】解:当时,,
故选:B.
把自变量x的值代入函数解析式进行计算即可得解.
本题考查了函数值的求解,是基础题,准确计算是解题的关键.
9.【答案】D
【解析】
【分析】
本题考查了用关系式表示的变量间关系,找出对应的关系式是解题的关键.
因为自变量的值为2,所以对应的关系式为,将代入该关系式即可得到结果.
【解答】
解:,所以对应的关系式为,
,即输出的y值为0.
故选D.
10.【答案】B
【解析】分析
主要考查了根据图形列出关系式据图示可知,第一层是4个,第二层是8个,第三层是12个,,第n层是4n个,即可确定y与n的关系.
详解
解:由图可知:
时,三角形有4个,即;
时,三角形有8个,即;
时,三角形有12个,即;
以此类推,
第n层为正整数三角形的个数:.
故选B.
11.【答案】
【解析】略
12.【答案】
【解析】
【分析】
本题考查了函数关系式,利用三角形的面积是解题关键.根据三角形的面积公式,可得答案.
【解答】
解:,,
,
故答案为.
13.【答案】
【解析】解:由表格可知,开始油箱中的油为,每行驶1小时,油量减少,
与t的关系式为,
故答案为.
14.【答案】解:?
180?
.
不可能.
理由:令,
解得.
因为x为整数,
所以总长度不可能为.
【解析】略
15.【答案】解:是自变量,N是因变量.
取大于2的整数.
当时,,故六边形的内角和为.
当边数每增加1时,多边形的内角和增加.
【解析】略
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
