2020--2021学年沪科版八年级数学下学期 19.2 平行四边形 同步练习试卷(Word版含答案)
文档属性
| 名称 | 2020--2021学年沪科版八年级数学下学期 19.2 平行四边形 同步练习试卷(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 09:16:53 | ||
图片预览



文档简介
19.2
平行四边形
一.选择题
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对角分别相等的四边形是平行四边形
2.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对角分别相等的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.如图,两条宽度分别为1和2的方形纸条交叉放置,重叠部分为四边形ABCD,若AB+BC=6,则四边形ABCD的面积是( )
A.4
B.2
C.8
D.6
4.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5
B.9
C.10
D.12
5.如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是( )
A.21
B.24
C.27
D.18
6.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d
B.a:b=c:d
C.ab=cd
D.ac=bd
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,?ABCD的对角线AC,BD交于点O,AD⊥BD,点E为AO的中点,若∠DAE=30°,DE=1,则?ABCD的周长为( )
A.
B.2
C.2+
D.2+2
9.已知平行四边形两邻边长16,20,若两个长边间距离为8,则两条短边间距离( )
A.4
B.5
C.10
D.8
10.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.AB∥CD,AB=CD
D.AB=AD,CB=CD
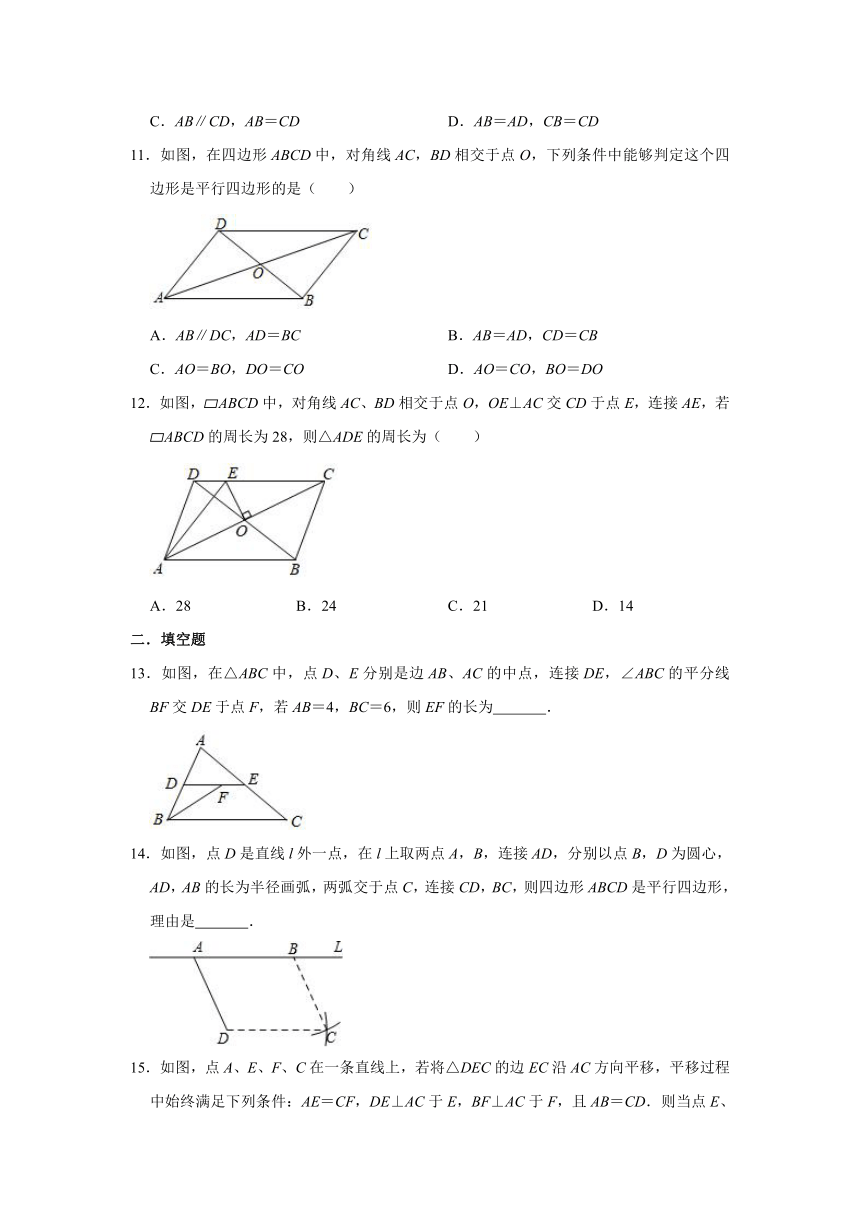
11.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中能够判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC
B.AB=AD,CD=CB
C.AO=BO,DO=CO
D.AO=CO,BO=DO
12.如图,?ABCD中,对角线AC、BD相交于点O,OE⊥AC交CD于点E,连接AE,若?ABCD的周长为28,则△ADE的周长为( )
A.28
B.24
C.21
D.14
二.填空题
13.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为
.
14.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是
.
15.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是
.
16.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED=
.
三.解答题
17.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
18.如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
参考答案
一.选择题
1.
A.
2.
D.
3.
A.
4.
B.
5.
A.
6.
D.
7.
C.
8.
D.
9.
C.
10.
C.
11.
D.
12.
D.
二.填空题
13.
1.
14.两组对边分别相等的四边形是平行四边形.
15.互相平分.
16.
126°.
三.解答题
17.(1)证明:如图,连接BD、AE,
∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分;
(2)解:∵FB=CE,
∴BE=2BF+FC,
∴BF===3,
∴AC=BF=3,BC=BF+FC=3+2=5,
∵AB⊥AC,
∴由勾股定理得:AB===4.
18.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF(ASA),
∴AF=EF;
(2)∵四边形ABCD为平行四边形,
∴OB=OD,
∵AF=CF,
∴OF是△ACE的中位线,
∴OF∥CE,CE=2OF,
∵AB=CD=CE,
∴AB=CD=CE=2OF,
∵AB∥CE,AB=CE,
∴四边形ABEC为平行四边形,
∴AC∥BE,
∵OF∥CE,
∴四边形OGEC为平行四边形,
∴OG=CE=2OF,
故图中长度是OF二倍的线段有AB,CD,CE,OG.
平行四边形
一.选择题
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对角分别相等的四边形是平行四边形
2.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对角分别相等的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.如图,两条宽度分别为1和2的方形纸条交叉放置,重叠部分为四边形ABCD,若AB+BC=6,则四边形ABCD的面积是( )
A.4
B.2
C.8
D.6
4.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5
B.9
C.10
D.12
5.如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是( )
A.21
B.24
C.27
D.18
6.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d
B.a:b=c:d
C.ab=cd
D.ac=bd
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,?ABCD的对角线AC,BD交于点O,AD⊥BD,点E为AO的中点,若∠DAE=30°,DE=1,则?ABCD的周长为( )
A.
B.2
C.2+
D.2+2
9.已知平行四边形两邻边长16,20,若两个长边间距离为8,则两条短边间距离( )
A.4
B.5
C.10
D.8
10.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.AB∥CD,AB=CD
D.AB=AD,CB=CD
11.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中能够判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC
B.AB=AD,CD=CB
C.AO=BO,DO=CO
D.AO=CO,BO=DO
12.如图,?ABCD中,对角线AC、BD相交于点O,OE⊥AC交CD于点E,连接AE,若?ABCD的周长为28,则△ADE的周长为( )
A.28
B.24
C.21
D.14
二.填空题
13.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为
.
14.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是
.
15.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是
.
16.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED=
.
三.解答题
17.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
18.如图,E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE交BC于点F,连接AC、BE.
(1)如图1,求证:AF=EF;
(2)连接BD交AC于点O,连接OF并延长交BE于点G,直接写出图中所有长度是OF二倍的线段.
参考答案
一.选择题
1.
A.
2.
D.
3.
A.
4.
B.
5.
A.
6.
D.
7.
C.
8.
D.
9.
C.
10.
C.
11.
D.
12.
D.
二.填空题
13.
1.
14.两组对边分别相等的四边形是平行四边形.
15.互相平分.
16.
126°.
三.解答题
17.(1)证明:如图,连接BD、AE,
∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分;
(2)解:∵FB=CE,
∴BE=2BF+FC,
∴BF===3,
∴AC=BF=3,BC=BF+FC=3+2=5,
∵AB⊥AC,
∴由勾股定理得:AB===4.
18.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF(ASA),
∴AF=EF;
(2)∵四边形ABCD为平行四边形,
∴OB=OD,
∵AF=CF,
∴OF是△ACE的中位线,
∴OF∥CE,CE=2OF,
∵AB=CD=CE,
∴AB=CD=CE=2OF,
∵AB∥CE,AB=CE,
∴四边形ABEC为平行四边形,
∴AC∥BE,
∵OF∥CE,
∴四边形OGEC为平行四边形,
∴OG=CE=2OF,
故图中长度是OF二倍的线段有AB,CD,CE,OG.
