2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》期中综合复习优生辅导训练(word附答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》期中综合复习优生辅导训练(word附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 11:31:34 | ||
图片预览



文档简介
2020-2021年度苏科版七年级数学下册《第9章整式乘法与因式分解》
期中综合复习优生辅导训练(附答案)
1.下列计算正确的是( )
A.(2x+y)(3x﹣y)=6x2﹣y2
B.(﹣x+2y)2=x2﹣4xy+4y2
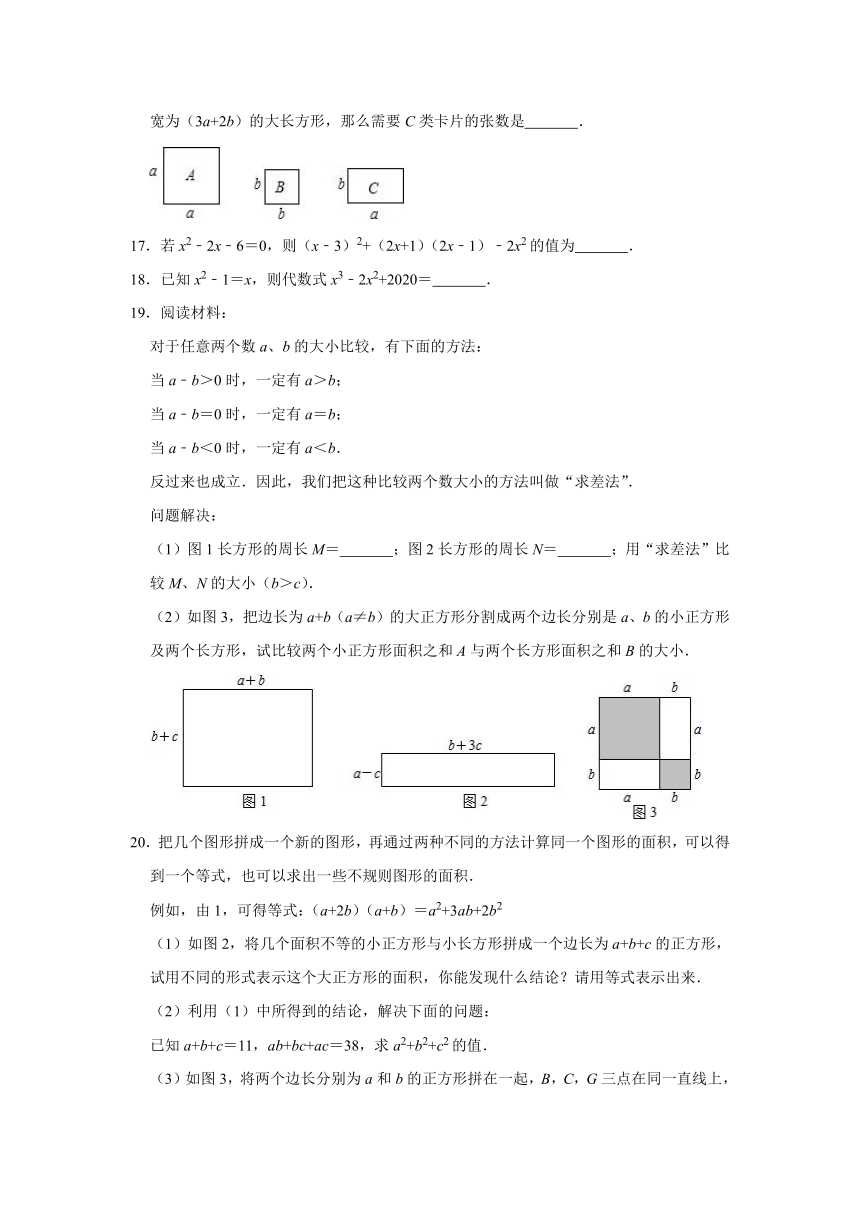
C.(m+n)3(m+n)2=m5+n5
D.(2x﹣y)2=4x2﹣xy+y2
2.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2
B.4cm2
C.5cm2
D.6cm2
3.已知a+b=3,ab=1,则多项式a2b+ab2﹣a﹣b的值为( )
A.﹣1
B.0
C.3
D.6
4.已知a=2018x+2018,b=2018x+2019,c=2018x+2020,则a2+b2+c2﹣ab﹣ac﹣bc的值是( )
A.0
B.1
C.2
D.3
5.将两张面积分别为64和36的正方形纸片按两种方式放置在矩形ABCD中,如图1,图2.AB=m,AD=n,条形波纹表示两正方形的重叠部分,L形阴影表示未被两张正方形纸片覆盖的部分,图1,图2中L形阴影部分的面积分别为S1,S2.则下列结论:①BF=m﹣8;②S1=mn﹣6m﹣16;③S2=mn﹣6n﹣16;④若m﹣n=2,则S2﹣S1=12.其中正确的个数是( )
A.1
B.2
C.3
D.4
6.下列各式:①﹣x2﹣y2;②﹣a2b2+1;
③a2+ab+b2;
④﹣x2+2xy﹣y2;⑤﹣mn+m2n2,用公式法分解因式的有( )
A.2个
B.3个
C.4个
D.5个
7.三种不同类型的地砖的长、宽如图所示,若现有A型地砖4块,B型地砖4块,C型地砖2块,要拼成一个正方形,则应去掉1块地砖;这样的地砖拼法可以得到一个关于m,n的恒等式为
.
8.计算:(1﹣)×(1﹣)×…×(1﹣)=
.
9.将两张边长分别为6和5的正方形纸片按图1和图2的两种方式放置在长方形ABCD内,长方形ABCD内未被这两张正方形纸片覆盖的部分用阴影表示,设图1中的阴影面积为S1,图2中的阴影面积为S2,当AD﹣AB=3时,S2﹣S1的值是
.
10.分解因式:(p+1)(p﹣4)+3p=
.
11.若(x2﹣x+m)(x﹣8)中不含x的一次项,则m的值为
.
12.已知(2x﹣a)(3x+2)=6x2﹣5x+b,则b=
.
13.若4x2﹣mx+49是一个完全平方式,则m的值为
.
14.如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=
.
15.下列有四个结论.其中正确的是
.
①若(x﹣1)x+1=1,则x只能是2;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=1;
③若a+b=10,ab=2,则a﹣b=2;
④若4x=a,8y=b,则23y﹣2x可表示.
16.如图.现有正方形卡片A类,B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b),宽为(3a+2b)的大长方形,那么需要C类卡片的张数是
.
17.若x2﹣2x﹣6=0,则(x﹣3)2+(2x+1)(2x﹣1)﹣2x2的值为
.
18.已知x2﹣1=x,则代数式x3﹣2x2+2020=
.
19.阅读材料:
对于任意两个数a、b的大小比较,有下面的方法:
当a﹣b>0时,一定有a>b;
当a﹣b=0时,一定有a=b;
当a﹣b<0时,一定有a<b.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
问题解决:
(1)图1长方形的周长M=
;图2长方形的周长N=
;用“求差法”比较M、N的大小(b>c).
(2)如图3,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较两个小正方形面积之和A与两个长方形面积之和B的大小.
20.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
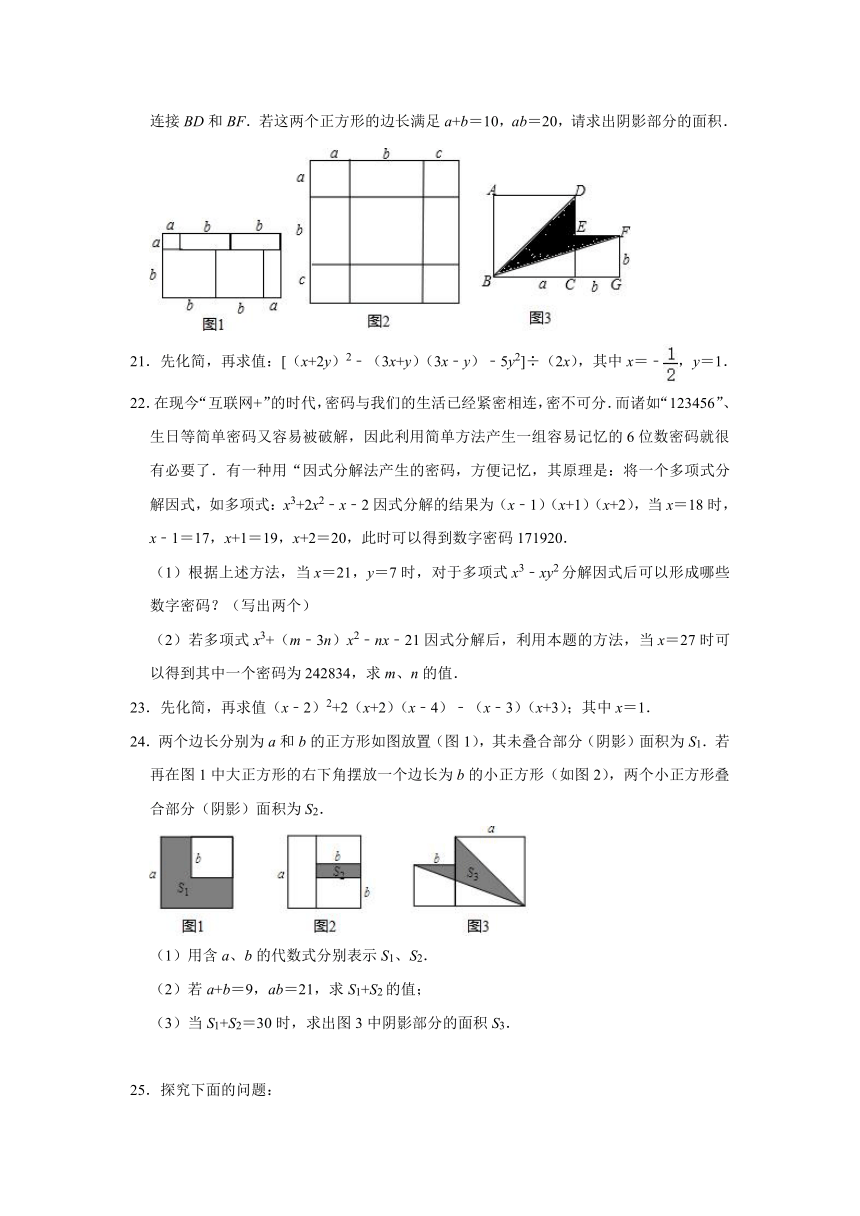
21.先化简,再求值:[(x+2y)2﹣(3x+y)(3x﹣y)﹣5y2]÷(2x),其中x=﹣,y=1.
22.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
23.先化简,再求值(x﹣2)2+2(x+2)(x﹣4)﹣(x﹣3)(x+3);其中x=1.
24.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1.若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2.
(2)若a+b=9,ab=21,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
25.探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是
(用式子表示),即乘法公式中的
公式.
(2)运用你所得到的公式计算:
①10.7×9.3
②(x+2y﹣3z)(x﹣2y﹣3z)
26.请仔细阅读下面某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程,然后回答问题:
解:令x2﹣4x+2=y,则:
原式=y(y+4)+4(第一步)
=y2+4y+4(第二步)
=(y+2)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的
;
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)另外一名同学发现第四步因式分解的结果不彻底,请你直接写出因式分解的最后结果
;
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
27.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为
.
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
28.教科书中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式x2+2x﹣3=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1);
求代数式2x2+4x﹣6的最小值,2x2+4x﹣6=2(x2+2x﹣3)=2(x+1)2﹣8.
可知当x=﹣1时,2x2+4x﹣6有最小值,最小值是﹣8,根据阅读材料用配方法解决下列问题:
(1)分解因式:x2﹣4x﹣5=
.
(2)当x为何值时,多项式﹣2x2﹣4x+3有最大值?并求出这个最大值.
参考答案
1.解:A.(2x+y)(3x﹣y)=6x2﹣2xy+3xy﹣y2=6x2+xy﹣y2,此选项计算错误;
B.(﹣x+2y)2=x2﹣4xy+4y2,此选项计算正确;
C.(m+n)3(m+n)2=(m+n)5,此选项计算错误;
D.(2x﹣y)2=4x2﹣2xy+y2,此选项计算错误;
故选:B.
2.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
3.解:a2b+ab2﹣a﹣b=(a2b﹣a)+(ab2﹣b)
=a(ab﹣1)+b(ab﹣1)=(ab﹣1)(a+b)
将a+b=3,ab=1代入,得
原式=0.
故选:B.
4.解:∵a=2018x+2018,b=2018x+2019,c=2018x+2020,
∴a﹣b=﹣1,a﹣c=﹣2,b﹣c=﹣1,
∴a2+b2+c2﹣ab﹣ac﹣bc=
=
===3,故选:D.
5.解:①BF=AB﹣AF=m﹣8,正确;
②,正确;
③,正确;
④若m﹣n=2,则S2﹣S1=mn﹣6n﹣16﹣(mn﹣6m﹣16)=6(m﹣n)=6×2=12,正确.故选:D.
6.解:①﹣x2﹣y2=﹣(x2+y2),因此①不能用公式法分解因式;
②﹣a2b2+1=1﹣(ab)2=(1+ab)(1﹣ab),因此②能用公式法分解因式;
③a2+ab+b2不符合完全平方公式的结果特征,因此③不能用公式法分解因式;
④﹣x2+2xy﹣y2=﹣(x2﹣2xy+y2)=﹣(x﹣y)2,因此④能用公式法分解因式;
⑤﹣mn+m2n2=(﹣mn)2,因此⑤能用公式法分解因式;
综上所述,能用公式法分解因式的有②④⑤,故选:B.
7.解:4块A的面积为:4×m×m=4m2;
4块B的面积为:4×m×n=4mn;
2块C的面积为2×n×n=2n2;
那么这三种类型的砖的总面积应该是:
4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2,
因此,多出了一块C型地砖,去掉一块C型地砖,这两个数的平方为(2m+n)2.
这样的地砖拼法可以得到一个关于m,n的恒等式为:4m2+4mn+n2=(2m+n)2
故答案为:4m2+4mn+n2=(2m+n)2.
8.解:原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)
=××××××…××=×=,
故答案为:.
9.解:设AB=CD=x,AD=BC=y,
则S1=6(AB﹣6)+(CD﹣5)(BC﹣6)=6(x﹣6)+(x﹣5)(y﹣6),
S2=6(BC﹣6)+(BC﹣5)(CD﹣6)=6(y﹣6)+(y﹣5)(x﹣6),
∴S2﹣S1=6(y﹣6)+(y﹣5)(x﹣6)﹣6(x﹣6)﹣(x﹣5)(y﹣6)
=6y﹣36+xy﹣6y﹣5x+30﹣6x+36﹣xy+6x+5y﹣30=5y﹣5x=5(y﹣x),
∵AD﹣AB=3,
∴y﹣x=3,
∴原式=5×3=15,
故答案为:15.
10.解:(p+1)(p﹣4)+3p=p2﹣3p﹣4+3p=p2﹣4=(p+2)(p﹣2).
11.解:(x2﹣x+m)(x﹣8)=x3﹣8x2﹣x2+8x+mx﹣8m=x3﹣9x2+(8+m)x﹣8m,
∵不含x的一次项,
∴8+m=0,
解得:m=﹣8.
故答案为﹣8.
12.解:∵(2x﹣a)(3x+2)=6x2﹣5x+b,
∴6x2+4x﹣3ax﹣2a=6x2﹣5x+b,
即6x2+(4﹣3a)x﹣2a=6x2﹣5x+b,
∴,
解得
故答案为:﹣6
13.解:∵(2x)2±28x+72=(2x±7)2,
∴﹣m=±28,
∴m=±28,
故答案为±28.
14.解:如图,连接BE,
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BC∥AM,
∴△AME与△AMB同底等高,
∴S△AME=S△AMB,
∴当AB=n时,△AME的面积记为Sn=;
Sn﹣1==﹣n+,
∴当n≥2时,Sn﹣Sn﹣1=﹣(﹣n+)=n﹣=,
∴S2020﹣S2019==.
故答案为:.
15.解:①若(x﹣1)x+1=1,则x是2或﹣1.故①错误;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,
∵(x﹣1)(x2+ax+1)=x3+(a﹣1)x2+(1﹣a)x﹣1,
∴a﹣1=0,解得a=1,故②正确;
③若a+b=10,ab=2,
∵(a﹣b)2=(a+b)2﹣4ab=100﹣8=92,
则a﹣b=2,故③错误;
④若4x=a,8y=b,则23y﹣2x=(23)y÷(22)x=8y÷4x=.故④正确.
所以其中正确的是②④.
故答案为:②④.
16.解:∵(a+3b)(3a+2b)=3a2+11ab+6b2,
∵一张C类卡片的面积为ab,
∴需要C类卡片11张.故答案为:11.
17.解:∵x2﹣2x﹣6=0,
∴x2﹣2x=6,
∴(x﹣3)2+(2x+1)(2x﹣1)﹣2x2=x2﹣6x+9+4x2﹣1﹣2x2
=3x2﹣6x+8=3(x2﹣2x)+8=3×6+8=26,故答案为:26.
18.解:x2﹣1=x,则x2﹣x=1,
x3﹣x2=x,
x3﹣2x2+2020=x3﹣x2﹣x2+2020=x﹣x2+2020=﹣1+2020=2019,
故答案为2019.
19.解:(1)图1长方形的周长M=2(a+b+b+c)=2a+4b+2c,
图2长方形的周长N=2(a﹣c+b+3c)=2a+2b+4c,
M﹣N=(2a+4b+2c)﹣(2a+2b+4c)=2b﹣2c,
∵b>c,∴2b>2c,
∴2b﹣2c>0,
∴M>N,
故答案为2a+4b+2c,2a+2b+4c,
(2)两个小正方形面积之和A=a2+b2,
两个长方形面积之和B=2ab,
a2+b2﹣2ab=(a﹣b)2,
∵a≠b,
∴a﹣b≠0,
∴A>B.
20.解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20.
21.解:原式=(x2+4xy+4y2﹣9x2+y2﹣5y2)÷2x=(﹣8x2+4xy)÷2x=﹣4x+2y,
当x=﹣、y=1时,
原式=﹣4×(﹣)+2×1=2+2=4.
22.解:(1)x3﹣xy2=x(x2﹣y2)=x(x+y)(x﹣y),
当x=21,y=7时,x+y=28,x﹣y=14,
∴可以形成的数字密码是:212814、211428;
(2)设x3+(m﹣3n)x2﹣nx﹣21=(x+p)(x+q)(x+r),
∵当x=27时可以得到其中一个密码为242834,
∴27+p=24,27+q=28,27+r=34,
解得,p=﹣3,q=1,r=7,
∴x3+(m﹣3n)x2﹣nx﹣21=(x﹣3)(x+1)(x+7),
∴x3+(m﹣3n)x2﹣nx﹣21=x3+5x2﹣17x﹣21,
∴,得,
即m的值是56,n的值是17.
23.解:原式=x2﹣4x+4+2(x2﹣2x﹣8)﹣(x2﹣9)
=x2﹣4x+4+2x2﹣4x﹣16﹣x2+9
=2x2﹣8x﹣3,
当x=1时,原式=2﹣8﹣3=﹣9.
24.解:(1)由图可得,S1=a2﹣b2,S2=2b2﹣ab.
(2)∵a+b=9,ab=21
∴S1+S2=a2﹣b2+2b2﹣ab
=a2+b2﹣ab=(a+b)2﹣3ab=81﹣3×21=18
∴S1+S2的值为18.
(3)由图可得:
S3=a2+b2﹣b(a+b)﹣=(
a2+b2﹣ab)
∵S1+S2=a2+b2﹣ab=30
∴S3=×30=15
∴图3中阴影部分的面积S3为15.
25.解:(1)图甲阴影面积=a2﹣b2,图乙阴影面积=(a+b)(a﹣b),
∴得到的公式为平方差公式:a2﹣b2=(a+b)(a﹣b);
故答案为:a2﹣b2=(a+b)(a﹣b);平方差;
(2)①10.7×9.3=(10+0.7)×(10﹣0.7)=102﹣0.72=100﹣0.49=99.51;
②(x+2y﹣3z)(x﹣2y﹣3z)=(x﹣3z+2y)(x﹣3z﹣2y)=(x﹣3z)2﹣(2y)2
=x2﹣6xz+9z2﹣4y2.
26.解:(1)运用了C,两数和的完全平方公式;故答案为:C;
(2)x2﹣4x+4还可以分解,分解不彻底;
(x2﹣4x+4)2=(x﹣2)4.
故答案为:(x﹣2)4.
(3)设x2﹣2x=y.
(x2﹣2x)(x2﹣2x+2)+1,=y(y+2)+1,=y2+2y+1,=(y+1)2,
=(x2﹣2x+1)2,=(x﹣1)4.
27.解:(1)设正方形A,B的边长分别为a,b(a>b),
由图甲得(a﹣b)2=1,由图乙得(a+b)2﹣a2﹣b2=12
得ab=6,a2+b2=13,
故答案为:13;
(2)∵ab=6,a2+b2=13,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
∵(a﹣b)2=1,
∴a﹣b=1,
∴图丙的阴影部分面积S=(2a+b)2﹣3a2﹣2b2=a2﹣b2+4ab=(a﹣b)(a+b)+4ab=5+24=29.
28.解:(1)x2﹣4x﹣5=(x﹣2)2﹣9=(x﹣2+3)(x﹣2﹣3)=(x+1)(x﹣5),
故答案为:(x+1)(x﹣5);
(2)∵﹣2x2﹣4x+3=﹣2(x+1)2+5,
∴当x=﹣1时,多项式﹣2x﹣4x+3有最大值,这个最大值是5;
期中综合复习优生辅导训练(附答案)
1.下列计算正确的是( )
A.(2x+y)(3x﹣y)=6x2﹣y2
B.(﹣x+2y)2=x2﹣4xy+4y2
C.(m+n)3(m+n)2=m5+n5
D.(2x﹣y)2=4x2﹣xy+y2
2.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2
B.4cm2
C.5cm2
D.6cm2
3.已知a+b=3,ab=1,则多项式a2b+ab2﹣a﹣b的值为( )
A.﹣1
B.0
C.3
D.6
4.已知a=2018x+2018,b=2018x+2019,c=2018x+2020,则a2+b2+c2﹣ab﹣ac﹣bc的值是( )
A.0
B.1
C.2
D.3
5.将两张面积分别为64和36的正方形纸片按两种方式放置在矩形ABCD中,如图1,图2.AB=m,AD=n,条形波纹表示两正方形的重叠部分,L形阴影表示未被两张正方形纸片覆盖的部分,图1,图2中L形阴影部分的面积分别为S1,S2.则下列结论:①BF=m﹣8;②S1=mn﹣6m﹣16;③S2=mn﹣6n﹣16;④若m﹣n=2,则S2﹣S1=12.其中正确的个数是( )
A.1
B.2
C.3
D.4
6.下列各式:①﹣x2﹣y2;②﹣a2b2+1;
③a2+ab+b2;
④﹣x2+2xy﹣y2;⑤﹣mn+m2n2,用公式法分解因式的有( )
A.2个
B.3个
C.4个
D.5个
7.三种不同类型的地砖的长、宽如图所示,若现有A型地砖4块,B型地砖4块,C型地砖2块,要拼成一个正方形,则应去掉1块地砖;这样的地砖拼法可以得到一个关于m,n的恒等式为
.
8.计算:(1﹣)×(1﹣)×…×(1﹣)=
.
9.将两张边长分别为6和5的正方形纸片按图1和图2的两种方式放置在长方形ABCD内,长方形ABCD内未被这两张正方形纸片覆盖的部分用阴影表示,设图1中的阴影面积为S1,图2中的阴影面积为S2,当AD﹣AB=3时,S2﹣S1的值是
.
10.分解因式:(p+1)(p﹣4)+3p=
.
11.若(x2﹣x+m)(x﹣8)中不含x的一次项,则m的值为
.
12.已知(2x﹣a)(3x+2)=6x2﹣5x+b,则b=
.
13.若4x2﹣mx+49是一个完全平方式,则m的值为
.
14.如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=
.
15.下列有四个结论.其中正确的是
.
①若(x﹣1)x+1=1,则x只能是2;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=1;
③若a+b=10,ab=2,则a﹣b=2;
④若4x=a,8y=b,则23y﹣2x可表示.
16.如图.现有正方形卡片A类,B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b),宽为(3a+2b)的大长方形,那么需要C类卡片的张数是
.
17.若x2﹣2x﹣6=0,则(x﹣3)2+(2x+1)(2x﹣1)﹣2x2的值为
.
18.已知x2﹣1=x,则代数式x3﹣2x2+2020=
.
19.阅读材料:
对于任意两个数a、b的大小比较,有下面的方法:
当a﹣b>0时,一定有a>b;
当a﹣b=0时,一定有a=b;
当a﹣b<0时,一定有a<b.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
问题解决:
(1)图1长方形的周长M=
;图2长方形的周长N=
;用“求差法”比较M、N的大小(b>c).
(2)如图3,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较两个小正方形面积之和A与两个长方形面积之和B的大小.
20.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
21.先化简,再求值:[(x+2y)2﹣(3x+y)(3x﹣y)﹣5y2]÷(2x),其中x=﹣,y=1.
22.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
23.先化简,再求值(x﹣2)2+2(x+2)(x﹣4)﹣(x﹣3)(x+3);其中x=1.
24.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1.若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2.
(2)若a+b=9,ab=21,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
25.探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是
(用式子表示),即乘法公式中的
公式.
(2)运用你所得到的公式计算:
①10.7×9.3
②(x+2y﹣3z)(x﹣2y﹣3z)
26.请仔细阅读下面某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程,然后回答问题:
解:令x2﹣4x+2=y,则:
原式=y(y+4)+4(第一步)
=y2+4y+4(第二步)
=(y+2)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的
;
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)另外一名同学发现第四步因式分解的结果不彻底,请你直接写出因式分解的最后结果
;
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
27.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为
.
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
28.教科书中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式x2+2x﹣3=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1);
求代数式2x2+4x﹣6的最小值,2x2+4x﹣6=2(x2+2x﹣3)=2(x+1)2﹣8.
可知当x=﹣1时,2x2+4x﹣6有最小值,最小值是﹣8,根据阅读材料用配方法解决下列问题:
(1)分解因式:x2﹣4x﹣5=
.
(2)当x为何值时,多项式﹣2x2﹣4x+3有最大值?并求出这个最大值.
参考答案
1.解:A.(2x+y)(3x﹣y)=6x2﹣2xy+3xy﹣y2=6x2+xy﹣y2,此选项计算错误;
B.(﹣x+2y)2=x2﹣4xy+4y2,此选项计算正确;
C.(m+n)3(m+n)2=(m+n)5,此选项计算错误;
D.(2x﹣y)2=4x2﹣2xy+y2,此选项计算错误;
故选:B.
2.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
3.解:a2b+ab2﹣a﹣b=(a2b﹣a)+(ab2﹣b)
=a(ab﹣1)+b(ab﹣1)=(ab﹣1)(a+b)
将a+b=3,ab=1代入,得
原式=0.
故选:B.
4.解:∵a=2018x+2018,b=2018x+2019,c=2018x+2020,
∴a﹣b=﹣1,a﹣c=﹣2,b﹣c=﹣1,
∴a2+b2+c2﹣ab﹣ac﹣bc=
=
===3,故选:D.
5.解:①BF=AB﹣AF=m﹣8,正确;
②,正确;
③,正确;
④若m﹣n=2,则S2﹣S1=mn﹣6n﹣16﹣(mn﹣6m﹣16)=6(m﹣n)=6×2=12,正确.故选:D.
6.解:①﹣x2﹣y2=﹣(x2+y2),因此①不能用公式法分解因式;
②﹣a2b2+1=1﹣(ab)2=(1+ab)(1﹣ab),因此②能用公式法分解因式;
③a2+ab+b2不符合完全平方公式的结果特征,因此③不能用公式法分解因式;
④﹣x2+2xy﹣y2=﹣(x2﹣2xy+y2)=﹣(x﹣y)2,因此④能用公式法分解因式;
⑤﹣mn+m2n2=(﹣mn)2,因此⑤能用公式法分解因式;
综上所述,能用公式法分解因式的有②④⑤,故选:B.
7.解:4块A的面积为:4×m×m=4m2;
4块B的面积为:4×m×n=4mn;
2块C的面积为2×n×n=2n2;
那么这三种类型的砖的总面积应该是:
4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2,
因此,多出了一块C型地砖,去掉一块C型地砖,这两个数的平方为(2m+n)2.
这样的地砖拼法可以得到一个关于m,n的恒等式为:4m2+4mn+n2=(2m+n)2
故答案为:4m2+4mn+n2=(2m+n)2.
8.解:原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)
=××××××…××=×=,
故答案为:.
9.解:设AB=CD=x,AD=BC=y,
则S1=6(AB﹣6)+(CD﹣5)(BC﹣6)=6(x﹣6)+(x﹣5)(y﹣6),
S2=6(BC﹣6)+(BC﹣5)(CD﹣6)=6(y﹣6)+(y﹣5)(x﹣6),
∴S2﹣S1=6(y﹣6)+(y﹣5)(x﹣6)﹣6(x﹣6)﹣(x﹣5)(y﹣6)
=6y﹣36+xy﹣6y﹣5x+30﹣6x+36﹣xy+6x+5y﹣30=5y﹣5x=5(y﹣x),
∵AD﹣AB=3,
∴y﹣x=3,
∴原式=5×3=15,
故答案为:15.
10.解:(p+1)(p﹣4)+3p=p2﹣3p﹣4+3p=p2﹣4=(p+2)(p﹣2).
11.解:(x2﹣x+m)(x﹣8)=x3﹣8x2﹣x2+8x+mx﹣8m=x3﹣9x2+(8+m)x﹣8m,
∵不含x的一次项,
∴8+m=0,
解得:m=﹣8.
故答案为﹣8.
12.解:∵(2x﹣a)(3x+2)=6x2﹣5x+b,
∴6x2+4x﹣3ax﹣2a=6x2﹣5x+b,
即6x2+(4﹣3a)x﹣2a=6x2﹣5x+b,
∴,
解得
故答案为:﹣6
13.解:∵(2x)2±28x+72=(2x±7)2,
∴﹣m=±28,
∴m=±28,
故答案为±28.
14.解:如图,连接BE,
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BC∥AM,
∴△AME与△AMB同底等高,
∴S△AME=S△AMB,
∴当AB=n时,△AME的面积记为Sn=;
Sn﹣1==﹣n+,
∴当n≥2时,Sn﹣Sn﹣1=﹣(﹣n+)=n﹣=,
∴S2020﹣S2019==.
故答案为:.
15.解:①若(x﹣1)x+1=1,则x是2或﹣1.故①错误;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,
∵(x﹣1)(x2+ax+1)=x3+(a﹣1)x2+(1﹣a)x﹣1,
∴a﹣1=0,解得a=1,故②正确;
③若a+b=10,ab=2,
∵(a﹣b)2=(a+b)2﹣4ab=100﹣8=92,
则a﹣b=2,故③错误;
④若4x=a,8y=b,则23y﹣2x=(23)y÷(22)x=8y÷4x=.故④正确.
所以其中正确的是②④.
故答案为:②④.
16.解:∵(a+3b)(3a+2b)=3a2+11ab+6b2,
∵一张C类卡片的面积为ab,
∴需要C类卡片11张.故答案为:11.
17.解:∵x2﹣2x﹣6=0,
∴x2﹣2x=6,
∴(x﹣3)2+(2x+1)(2x﹣1)﹣2x2=x2﹣6x+9+4x2﹣1﹣2x2
=3x2﹣6x+8=3(x2﹣2x)+8=3×6+8=26,故答案为:26.
18.解:x2﹣1=x,则x2﹣x=1,
x3﹣x2=x,
x3﹣2x2+2020=x3﹣x2﹣x2+2020=x﹣x2+2020=﹣1+2020=2019,
故答案为2019.
19.解:(1)图1长方形的周长M=2(a+b+b+c)=2a+4b+2c,
图2长方形的周长N=2(a﹣c+b+3c)=2a+2b+4c,
M﹣N=(2a+4b+2c)﹣(2a+2b+4c)=2b﹣2c,
∵b>c,∴2b>2c,
∴2b﹣2c>0,
∴M>N,
故答案为2a+4b+2c,2a+2b+4c,
(2)两个小正方形面积之和A=a2+b2,
两个长方形面积之和B=2ab,
a2+b2﹣2ab=(a﹣b)2,
∵a≠b,
∴a﹣b≠0,
∴A>B.
20.解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20.
21.解:原式=(x2+4xy+4y2﹣9x2+y2﹣5y2)÷2x=(﹣8x2+4xy)÷2x=﹣4x+2y,
当x=﹣、y=1时,
原式=﹣4×(﹣)+2×1=2+2=4.
22.解:(1)x3﹣xy2=x(x2﹣y2)=x(x+y)(x﹣y),
当x=21,y=7时,x+y=28,x﹣y=14,
∴可以形成的数字密码是:212814、211428;
(2)设x3+(m﹣3n)x2﹣nx﹣21=(x+p)(x+q)(x+r),
∵当x=27时可以得到其中一个密码为242834,
∴27+p=24,27+q=28,27+r=34,
解得,p=﹣3,q=1,r=7,
∴x3+(m﹣3n)x2﹣nx﹣21=(x﹣3)(x+1)(x+7),
∴x3+(m﹣3n)x2﹣nx﹣21=x3+5x2﹣17x﹣21,
∴,得,
即m的值是56,n的值是17.
23.解:原式=x2﹣4x+4+2(x2﹣2x﹣8)﹣(x2﹣9)
=x2﹣4x+4+2x2﹣4x﹣16﹣x2+9
=2x2﹣8x﹣3,
当x=1时,原式=2﹣8﹣3=﹣9.
24.解:(1)由图可得,S1=a2﹣b2,S2=2b2﹣ab.
(2)∵a+b=9,ab=21
∴S1+S2=a2﹣b2+2b2﹣ab
=a2+b2﹣ab=(a+b)2﹣3ab=81﹣3×21=18
∴S1+S2的值为18.
(3)由图可得:
S3=a2+b2﹣b(a+b)﹣=(
a2+b2﹣ab)
∵S1+S2=a2+b2﹣ab=30
∴S3=×30=15
∴图3中阴影部分的面积S3为15.
25.解:(1)图甲阴影面积=a2﹣b2,图乙阴影面积=(a+b)(a﹣b),
∴得到的公式为平方差公式:a2﹣b2=(a+b)(a﹣b);
故答案为:a2﹣b2=(a+b)(a﹣b);平方差;
(2)①10.7×9.3=(10+0.7)×(10﹣0.7)=102﹣0.72=100﹣0.49=99.51;
②(x+2y﹣3z)(x﹣2y﹣3z)=(x﹣3z+2y)(x﹣3z﹣2y)=(x﹣3z)2﹣(2y)2
=x2﹣6xz+9z2﹣4y2.
26.解:(1)运用了C,两数和的完全平方公式;故答案为:C;
(2)x2﹣4x+4还可以分解,分解不彻底;
(x2﹣4x+4)2=(x﹣2)4.
故答案为:(x﹣2)4.
(3)设x2﹣2x=y.
(x2﹣2x)(x2﹣2x+2)+1,=y(y+2)+1,=y2+2y+1,=(y+1)2,
=(x2﹣2x+1)2,=(x﹣1)4.
27.解:(1)设正方形A,B的边长分别为a,b(a>b),
由图甲得(a﹣b)2=1,由图乙得(a+b)2﹣a2﹣b2=12
得ab=6,a2+b2=13,
故答案为:13;
(2)∵ab=6,a2+b2=13,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
∵(a﹣b)2=1,
∴a﹣b=1,
∴图丙的阴影部分面积S=(2a+b)2﹣3a2﹣2b2=a2﹣b2+4ab=(a﹣b)(a+b)+4ab=5+24=29.
28.解:(1)x2﹣4x﹣5=(x﹣2)2﹣9=(x﹣2+3)(x﹣2﹣3)=(x+1)(x﹣5),
故答案为:(x+1)(x﹣5);
(2)∵﹣2x2﹣4x+3=﹣2(x+1)2+5,
∴当x=﹣1时,多项式﹣2x﹣4x+3有最大值,这个最大值是5;
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
