2020-2021学年人教版七年级数学下册 9.1.1 不等式及其解集(共34张ppt)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 9.1.1 不等式及其解集(共34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 07:34:10 | ||
图片预览







文档简介
(共34张PPT)
9.1.1
不等式及其解集
第九章
不等式与不等式组
1
2
3
二、学习目标
认识不等号,了解不等式概念,能正确列出含未知数的不等式
理解并区别不等式的解及解集,能用数轴正确表示不等式的解集;
感悟数形结合思想、建模思想,体会类比思想、集合思想
某食品标签上标示:酒精度≥10%。
体检单上某人的体重:体重
≤65kg
“≤”小于或等于
“≥”大于或等于
青少年请勿喝酒。有害健康
实际问题
?数学式子
已知一辆匀速行驶的汽车,在11:20距离A地50km,若该车实际上在中午12:00之前驶过A地,车速应满足什么条件?
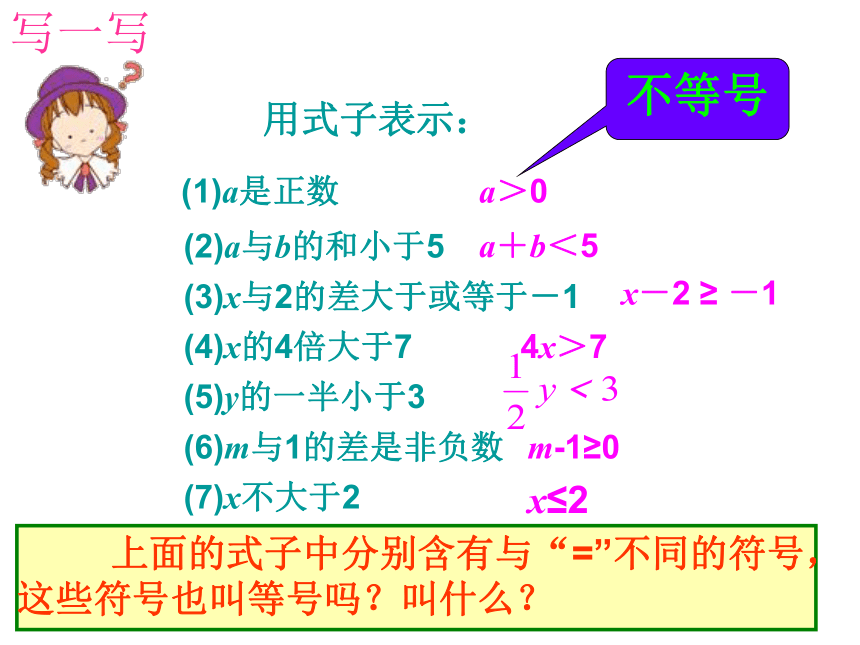
用式子表示:
(1)a是正数
(2)a与b的和小于5
(3)x与2的差大于或等于-1
(4)x的4倍大于7
(5)y的一半小于3
a>0
a+b<5
x-2
≥
-1
4x>7
(6)m与1的差是非负数
(7)x不大于2
m-1≥0
x≤2
写一写
上面的式子中分别含有与“=”不同的符号,这些符号也叫等号吗?叫什么?
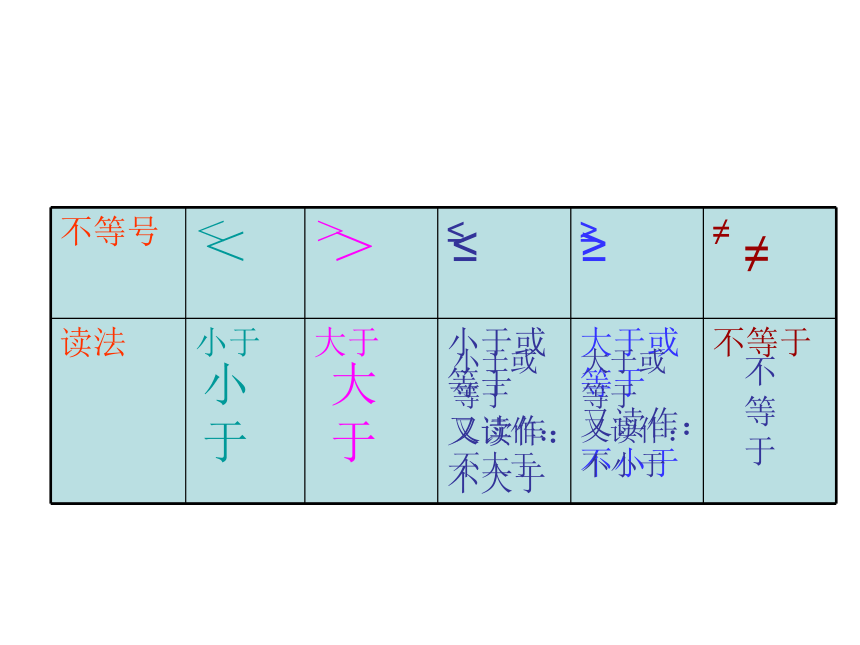
不等号
不等号
<
>
≤
≥
≠
读法
小于
大于
小于或等于
又读作:
不大于
大于或等于
又读作:不小于
不等于
<
小于
>
大于
≤
小于或等于
又读作:
不大于
≥
大于或等于
又读作:
不小于
≠
不
等
于
a>0
a+b<5
x-2
≥
-1
4x>7
m-1≥0
x≤2
a+2≠2
这些式子有什么共同特征?
1<2
x≥10%
y≤65
5≠-100
不等式
用“=”号表示相等关系的式子叫等式
用不等号“<”或“>”表示大小关系的式子,叫做不等式。
用“≠”表示不等关系的式子也是不等式。
用“≥”或“≤”
表示两个数量的大小关系的式子仍是不等式。
以上三条可以归纳为:
用不等号表示不等关系的式子,叫做不等式。
类比方程的解
类比方程
的解的定义,
给不等式的解下定义?
下列各数:-4,10,-
0.5
,
5,0,7.9,2,
3.5
我们知道:使方程左右两边相等的未知数的值叫做方程的解
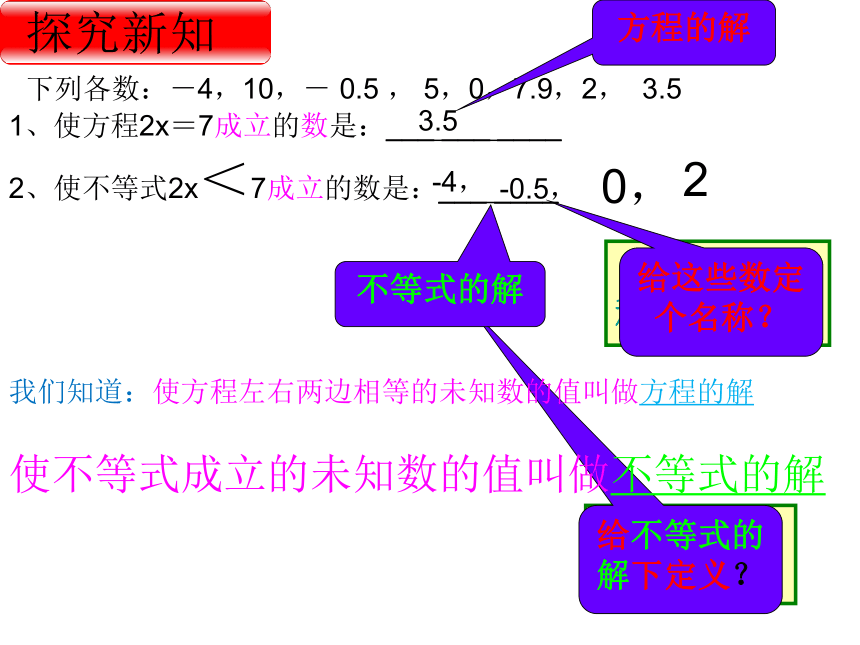
探究新知
2、使不等式2x<7成立的数是:___
____
1、使方程2x=7成立的数是:___
___
____
使不等式成立的未知数的值叫做不等式的解
-4,
3.5
-0.5,
0,
2
方程的解
给这些数定个名称?
不等式的解
从完成表格时发现,2x<7的解有多少个?
从表格的数据发现,不等式2x<7的解必须满足什么条件?
小于3.5能说是不等式2X<7的解吗?
小于3.5是不等式2X<7的解吗?
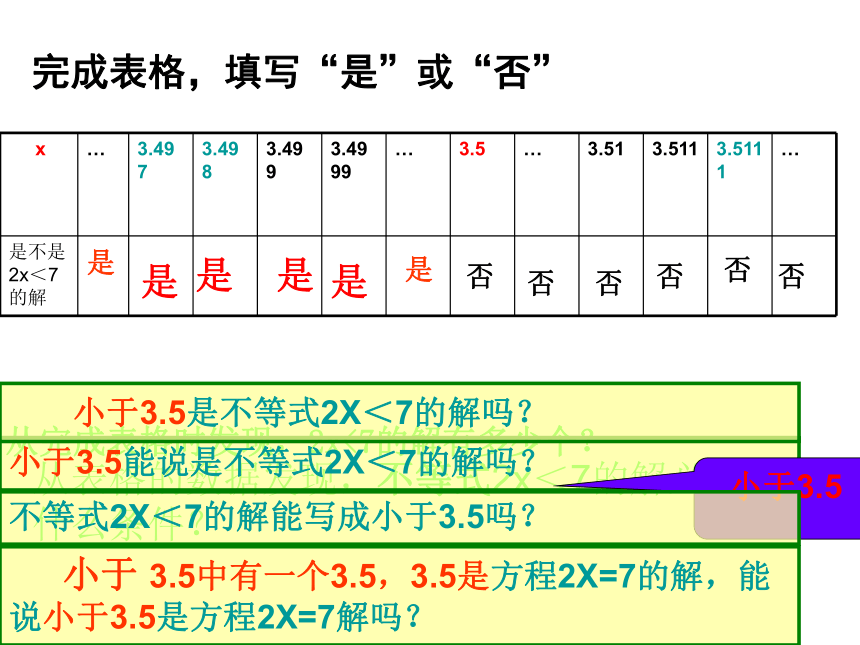
完成表格,填写“是”或“否”
x
…
3.497
3.498
3.499
3.4999
…
3.5
…
3.51
3.511
3.5111
…
是不是2x<7的解
是
是
是
是
否
否
否
否
否
否
是
是
小于3.5
小于
3.5中有一个3.5,3.5是方程2X=7的解,能说小于3.5是方程2X=7解吗?
不等式2X<7的解能写成小于3.5吗?
由探究得知:不等式2x<7的解有无数个。小于3.5的任何一个数都是它的一个解。
不等式的所有的解,能组成一个集合
给这个集合起个什么名称呢?
不等式的解集
小于3.5是不等式2X<7的解集
集合中的每一个数值都是解
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称为这个
我们知道了,一方面,把不等式的解,全都集中起来,可以形成一个集合;另一方面,这个集合中,每一个数值都是不等式的解。
换一句话来说,也可以理解为:
能够使不等式成立的所有数值都在这个集合里。集合中的每一个数值都能够使不等式成立。
不等式的解集。
1.下列说法正确的是(
)
(A)x=3.5是2x<7的解集
(B)x=3.5是2x<7的解
(C)x=3是2x
<
7的唯一解
(D)x<3.5是2x<7的解集
D
2.下列说法错误的是(
)
(A)X=3.1是x+3>6的一个解
(B)x+1<2的解有无数个
(C)x+1<4的解集是x<2
(D)x+2>1的解集是x>-1
C
3.下列说法不正确的是(
)
(A)方程2X+3=1的解是X=-1
(B)x=-1是方程2X+3=1的解
(C)不等式2x+3>1的解是x=3
(D)x=3是不等式2x+3>1的解
C
4、判断下列说法是否正确:
(1)x
=
-1是不等式x
<
1的一个解
(2)x
=
2是不等式x
–
1
>
0的解集
(3)不等式x
+
3
>6的解是x>3
(4)不等式1
–
x
<
0的解有无数多个数
(5)x
–
5
<
1的解是x
=
2
(6)x
=
0是不等式x
≥
0的解
概念辨析
直接写出不等式的解集:
⑴x+3>6;
⑵2x<8;
⑶x-2≥9.
x>3
x<4
x≥11
求不等式的
解集
的过程叫做解不等式
求方程的
解
的过程叫做解方程
上面写出不等式的解集的过程是解方程吗?
类比解方程的概念,我们得到:解不等式的概念
再探究
实数与数轴上的点是一一对应的
再探究
X
…
-1
0
1
2
2.5
3
3.1
3.2
3.3
3.4
3.5
4
5
6
…
2X<7
?
?
?
?
?
2.5
?
?
3.1
?
3.2
?
?
3.3
3.4
?
?
3.5
?
?
这里表示的不都是不等式的解,如何表示解集呢?
?
?
?
?
再探究
x
…
…
2x<7
?
?
?
?
?
2.5
?
?
3
3.1
?
3.2
?
3.3
?
3.4
?
3.5
3.6
3.7
3.8
3.7
3.5
3.6
3.8
O
3.5
3.5
︱
?
?
?
?
?
?
————
这样表示不等式的解集呢?
小于向左画
画一画:
利用数轴来表示下列不等式的解集.
(1)x>-1
(2)x<
0
-1
1
0
1
2
(3)X≥-1
0
-1
1
●
实心圆:
表示-1在这个解集内
空心圆:
表示-1不在这个解集内
大于向右画;
大于向右画,小于向左画;
有等号的画实心圆点,无等号的画空心圆圈.
︱
画数轴
找点
定界
牵方向
用数轴表示x+2≥5的解集x≥3的步骤:
。
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
?
一、语言表达。
如:X的取值范围是小于-2。
二、式子表现。如
X<-2。
三、数轴表示。如:
0
-1
-2
不等式的解集的表示方法有三种:
在数轴上表示x≥-2正确的是
(
)
-2
A
●
0
-2
B
●
○
0
-2
C
●
0
-2
D
D
用不等式表示图1中的解集,其中正确的是(
).
C
A
x>-2
B
x<-2
C
x≥-2
D
x≤-2
D
下图中表示的是不等式的解集,其中错误的是
(
).
A
x≤2
B
x>1
C
x≠0
D
x<0
已知x的取值范围如图所示,
你能写出x的取值范围吗?
0
-1
-2
答:x<-2
下列说法中,正确的是(
)
(A)X=-3是不等式X+4<1的解
(B)X>1.5是-2X
>
-3的解集
(C)X
>-5
的负整数解有无数多个
(D)X
<7的非正整数解有无数多个
D
在平面直角坐标系中,点P(a,b-5)在第四象限,
则a、b的取值范围分别是
______________
a>0,b<5
不等式X≤a正偶数解是2,4,
则a的取值范围是____________________
4≤a<6
说一说
你的收获
不等式
不等号
不等思想
不等式的解
不等式的解集
解集在数轴上表示
知识思维导图
实际问题
本节课结合实际问题中不等关系,通过类比,引出不等式、不等式的解、不等式的解集,继而用数轴表示不等式的解集。
不等式既是现阶段学习的重点内容,也是后续学习的重要基础。
Thank
you!
谢谢同学们的努力!
谢谢指导!
9.1.1
不等式及其解集
第九章
不等式与不等式组
1
2
3
二、学习目标
认识不等号,了解不等式概念,能正确列出含未知数的不等式
理解并区别不等式的解及解集,能用数轴正确表示不等式的解集;
感悟数形结合思想、建模思想,体会类比思想、集合思想
某食品标签上标示:酒精度≥10%。
体检单上某人的体重:体重
≤65kg
“≤”小于或等于
“≥”大于或等于
青少年请勿喝酒。有害健康
实际问题
?数学式子
已知一辆匀速行驶的汽车,在11:20距离A地50km,若该车实际上在中午12:00之前驶过A地,车速应满足什么条件?
用式子表示:
(1)a是正数
(2)a与b的和小于5
(3)x与2的差大于或等于-1
(4)x的4倍大于7
(5)y的一半小于3
a>0
a+b<5
x-2
≥
-1
4x>7
(6)m与1的差是非负数
(7)x不大于2
m-1≥0
x≤2
写一写
上面的式子中分别含有与“=”不同的符号,这些符号也叫等号吗?叫什么?
不等号
不等号
<
>
≤
≥
≠
读法
小于
大于
小于或等于
又读作:
不大于
大于或等于
又读作:不小于
不等于
<
小于
>
大于
≤
小于或等于
又读作:
不大于
≥
大于或等于
又读作:
不小于
≠
不
等
于
a>0
a+b<5
x-2
≥
-1
4x>7
m-1≥0
x≤2
a+2≠2
这些式子有什么共同特征?
1<2
x≥10%
y≤65
5≠-100
不等式
用“=”号表示相等关系的式子叫等式
用不等号“<”或“>”表示大小关系的式子,叫做不等式。
用“≠”表示不等关系的式子也是不等式。
用“≥”或“≤”
表示两个数量的大小关系的式子仍是不等式。
以上三条可以归纳为:
用不等号表示不等关系的式子,叫做不等式。
类比方程的解
类比方程
的解的定义,
给不等式的解下定义?
下列各数:-4,10,-
0.5
,
5,0,7.9,2,
3.5
我们知道:使方程左右两边相等的未知数的值叫做方程的解
探究新知
2、使不等式2x<7成立的数是:___
____
1、使方程2x=7成立的数是:___
___
____
使不等式成立的未知数的值叫做不等式的解
-4,
3.5
-0.5,
0,
2
方程的解
给这些数定个名称?
不等式的解
从完成表格时发现,2x<7的解有多少个?
从表格的数据发现,不等式2x<7的解必须满足什么条件?
小于3.5能说是不等式2X<7的解吗?
小于3.5是不等式2X<7的解吗?
完成表格,填写“是”或“否”
x
…
3.497
3.498
3.499
3.4999
…
3.5
…
3.51
3.511
3.5111
…
是不是2x<7的解
是
是
是
是
否
否
否
否
否
否
是
是
小于3.5
小于
3.5中有一个3.5,3.5是方程2X=7的解,能说小于3.5是方程2X=7解吗?
不等式2X<7的解能写成小于3.5吗?
由探究得知:不等式2x<7的解有无数个。小于3.5的任何一个数都是它的一个解。
不等式的所有的解,能组成一个集合
给这个集合起个什么名称呢?
不等式的解集
小于3.5是不等式2X<7的解集
集合中的每一个数值都是解
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称为这个
我们知道了,一方面,把不等式的解,全都集中起来,可以形成一个集合;另一方面,这个集合中,每一个数值都是不等式的解。
换一句话来说,也可以理解为:
能够使不等式成立的所有数值都在这个集合里。集合中的每一个数值都能够使不等式成立。
不等式的解集。
1.下列说法正确的是(
)
(A)x=3.5是2x<7的解集
(B)x=3.5是2x<7的解
(C)x=3是2x
<
7的唯一解
(D)x<3.5是2x<7的解集
D
2.下列说法错误的是(
)
(A)X=3.1是x+3>6的一个解
(B)x+1<2的解有无数个
(C)x+1<4的解集是x<2
(D)x+2>1的解集是x>-1
C
3.下列说法不正确的是(
)
(A)方程2X+3=1的解是X=-1
(B)x=-1是方程2X+3=1的解
(C)不等式2x+3>1的解是x=3
(D)x=3是不等式2x+3>1的解
C
4、判断下列说法是否正确:
(1)x
=
-1是不等式x
<
1的一个解
(2)x
=
2是不等式x
–
1
>
0的解集
(3)不等式x
+
3
>6的解是x>3
(4)不等式1
–
x
<
0的解有无数多个数
(5)x
–
5
<
1的解是x
=
2
(6)x
=
0是不等式x
≥
0的解
概念辨析
直接写出不等式的解集:
⑴x+3>6;
⑵2x<8;
⑶x-2≥9.
x>3
x<4
x≥11
求不等式的
解集
的过程叫做解不等式
求方程的
解
的过程叫做解方程
上面写出不等式的解集的过程是解方程吗?
类比解方程的概念,我们得到:解不等式的概念
再探究
实数与数轴上的点是一一对应的
再探究
X
…
-1
0
1
2
2.5
3
3.1
3.2
3.3
3.4
3.5
4
5
6
…
2X<7
?
?
?
?
?
2.5
?
?
3.1
?
3.2
?
?
3.3
3.4
?
?
3.5
?
?
这里表示的不都是不等式的解,如何表示解集呢?
?
?
?
?
再探究
x
…
…
2x<7
?
?
?
?
?
2.5
?
?
3
3.1
?
3.2
?
3.3
?
3.4
?
3.5
3.6
3.7
3.8
3.7
3.5
3.6
3.8
O
3.5
3.5
︱
?
?
?
?
?
?
————
这样表示不等式的解集呢?
小于向左画
画一画:
利用数轴来表示下列不等式的解集.
(1)x>-1
(2)x<
0
-1
1
0
1
2
(3)X≥-1
0
-1
1
●
实心圆:
表示-1在这个解集内
空心圆:
表示-1不在这个解集内
大于向右画;
大于向右画,小于向左画;
有等号的画实心圆点,无等号的画空心圆圈.
︱
画数轴
找点
定界
牵方向
用数轴表示x+2≥5的解集x≥3的步骤:
。
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
?
一、语言表达。
如:X的取值范围是小于-2。
二、式子表现。如
X<-2。
三、数轴表示。如:
0
-1
-2
不等式的解集的表示方法有三种:
在数轴上表示x≥-2正确的是
(
)
-2
A
●
0
-2
B
●
○
0
-2
C
●
0
-2
D
D
用不等式表示图1中的解集,其中正确的是(
).
C
A
x>-2
B
x<-2
C
x≥-2
D
x≤-2
D
下图中表示的是不等式的解集,其中错误的是
(
).
A
x≤2
B
x>1
C
x≠0
D
x<0
已知x的取值范围如图所示,
你能写出x的取值范围吗?
0
-1
-2
答:x<-2
下列说法中,正确的是(
)
(A)X=-3是不等式X+4<1的解
(B)X>1.5是-2X
>
-3的解集
(C)X
>-5
的负整数解有无数多个
(D)X
<7的非正整数解有无数多个
D
在平面直角坐标系中,点P(a,b-5)在第四象限,
则a、b的取值范围分别是
______________
a>0,b<5
不等式X≤a正偶数解是2,4,
则a的取值范围是____________________
4≤a<6
说一说
你的收获
不等式
不等号
不等思想
不等式的解
不等式的解集
解集在数轴上表示
知识思维导图
实际问题
本节课结合实际问题中不等关系,通过类比,引出不等式、不等式的解、不等式的解集,继而用数轴表示不等式的解集。
不等式既是现阶段学习的重点内容,也是后续学习的重要基础。
Thank
you!
谢谢同学们的努力!
谢谢指导!
